THE BLOCH SPACE ON THE UNIT BALL OF A HILBERT SPACE:MAXIMALITY AND MULTIPLIERS?
Departamento de Análisis Matemático,Universidad de Valencia.C/Dr.Moliner 50.46.100,Burjasot,Valencia,Spain
E-mail:galindo@uv.es
Mikael LINDSTR?M
Department of Mathematics,Abo Akademi University.FI-20500?Abo,Finland
E-mail:mikael.lindstrom@abo.fi
Abstract We prove that,as in the finite dimensional case,the space of Bloch functions on the unit ball of a Hilbert space contains,under very mild conditions,any semi-Banach space of analytic functions invariant under automorphisms.The multipliers for such Bloch space are characterized and some of their spectral properties are described.
Key words Analytic functions on Hilbert space,invariance under automorphisms,multiplier
1 Introduction
All over(X,‖·‖)denotes a semi-Banach space of analytic functions on the unit ball of a Hilbert space H that is invariant under automorphisms ? of the ball BHin the sense that for all f∈X,we have
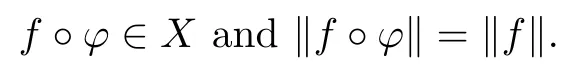
A function f:BH→C is said to be a Bloch function[2]if
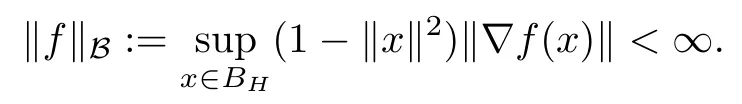
By B(BH),we denote the space of Bloch functions defined on BH.We will consider,besides the semi-norm‖·‖B,the semi-norm
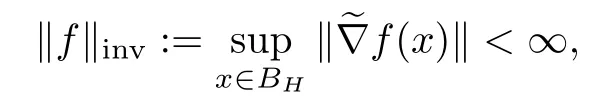
where the invariant gradientf is defined byf(a)=?(f°?a)(0)for any a∈BH(see the definition of the automorphism ?abelow).Both semi-norms were shown to be equivalent[2,Theorem 3.8]and render B(BH)a semi-Banach space.The latter semi-norm‖f‖invis invariant under automorphisms.So,B(BH)is invariant under automorphisms of BH.Associated to these semi-norms,there are the corresponding(equivalent)norms,
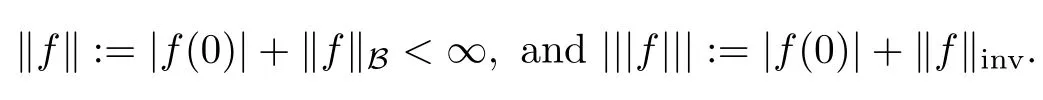
In this note it is proved that any other invariant space(X,‖·‖)possesing a nontrivial linear functional continuous for the compact open topology is continuously embedded in B(BH).This was already proved in 1982 by R.Timoney[7]for finite dimensional Hilbert spaces and recalled in K.Zhu’s book[9],whose proof inspired strongly ours,in spite that there is a missing assumption in the result’s statement.Also the multipliers of the Bloch space are characterized,and the invertibility,spectrum and essential spectrum of the linear operators that they give raise to are described.
A summary about automorphisms of the unit ball BHis as follows:The analogues of M?bius transformations on H are the mappings ?a:BH→BH,a∈BH,which is defined according to

The automorphisms of BHturn to be compositions of such analogous Mbius transformations with unitary transformations U of H,that is,self-maps of H satisfying〈U(x),U(y)〉=〈x,y〉for all x,y∈H.
The pseudo-hyperbolic and hyperbolic metrics on BHare,respectively,defined by
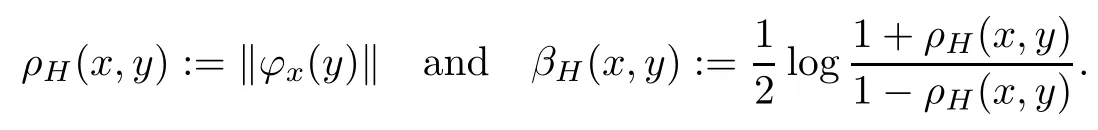
By H(BH)we denote the space of complex-valued analytic functions on BH,and by H∞(BH)the subspace of H(BH)of bounded functions endowed with the norm,denoted‖·‖∞,of uniform convergence on BH.It is known that H∞(BH)?B(BH)with continuous inclusion[2].For background on analytic functions,we refer to[8].
2 Maximality
Before proving our main result Theorem 2.2,we show some others that we need.
Lemma 2.1(a)Every term in the Taylor series of f∈X belongs to X as well.
(b)If there is a non-constant function g∈X,then every continuous linear functional on H lies in X.
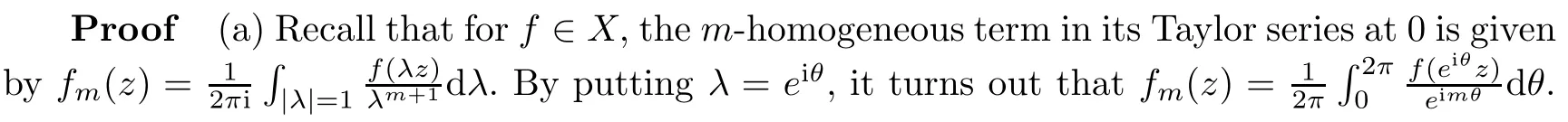

Consequently,every f∈X is constant.This is in contrary to the assumption,so there is a norm one linear functional υ in H which belongs to X.
Since the dual space of a Hilbert space is also a Hilbert space,any norm one linear functional in H can be obtained by composing υ with a suitable unitary transformation that is,of course,an automorphism of the ball. □
Recall that a(continuous)finite type polynomial on a normed space E is a linear combination of powers of functionals in the dual space E?.
Proposition 2.1If there is a non-constant function g∈X,then all finite polynomials lie in X.
ProofAccording to Lemma 2.1(b),for each a∈BH,the linear functional a?(z)=〈z,a〉is an element of X.Thus a?°?a∈X.Since
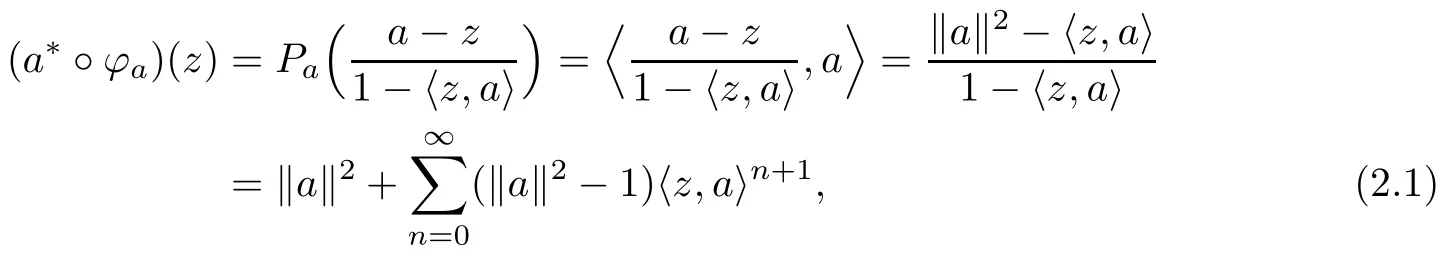
we apply Lemma 2.1(a)to assure that the powers of the linear functional a?are in X.Hence,the finite type polynomials belong to X. □
Theorem 2.2Assume that in the semi-Banach space X there is a nonconstant function,and that there is a nonzero linear functional L on X that is continuous for the compact open topology τ0.Then X?B(BH).If further L(1)/=0,then X?H∞(BH).
ProofWe first assume that L(1)=0.Let e be a vector in some orthonormal basis of H.We show by contradiction that there exists an automorphism ? of BHsuch that for the linear functional L?:=L°C?,one has L?(e?)/=0,where C?is the composition operator given by right composition with ?.
So assume that L?(e?)=0 for all automorphisms ? of BH.Set a=re,0 Since this series is τ0convergent,we have,for all 0 Hence,L((e?)k)=L(〈·,e〉k)=0 for all k∈N. For any other element w∈H,w/=0,‖w‖=1,there is an isometric isomorphism–and also an automorphism of the ball–ψ of H exchanging e and w,so for all automorphisms ?,L?(w?)=L?(e?°ψ)=Lψ°?(e?)=0.Therefore,we argue as in the paragraph above to conclude that L((w?)k)=0 for all k∈N. Then by linearity,L(P)=0,for all finite type polynomials P in H.And bearing in mind that the finite type polynomials are τ0-dense in the space H(BH)([8,28.1 Theorem]),then L(f)=0 for all f∈X.This is a contradiction. Therefore,we may assume,since all L?are also τ0-continuous,that L(e?)/=0. This allows us to use the Lebesgue domination convergence theorem to guarantee that L(f(eit·))defines an element in L1([0,2π]).The fact that L is τ0-continuous implies that there is compact subset M of BH,which we can suppose to be balanced,and A>0,such that Since f1(z)=〈z,?f(0)〉=?f(0)?(z),we conclude that F(f)=L(?f(0)?),and that there is a constant C>0 such that A few months later, the wife came to the husband with a proposal, I read in a magazine, a while ago, about how we can strengthen our marriage, she offered. Each of us will write a list of the things that we find a bit annoying with the other person. Then, we can talk about how we can fix them together and make our lives happier together. Now,inequality(2.2)yields An inequality also valid if?f(0)=0.And now for the invariant gradient, which shows that f∈B(BH). Recall that a function f is said to be a multiplier for the Bloch space if fg∈B(BH)for all g∈B(BH). The key to characterize the multipliers for the Bloch space in the n-ball Bnis the following result that for x,y∈Bnwe have where β is the Bergman or hyperbolic metric in Bnand f:Bn→C is an analytic function on Bn. Theorem 3.1Let f∈H(BH).Then,f is a multiplier of the Bloch space B(BH)if and only if f∈H∞(BH)and the functionis bounded. ProofIf f is a multiplier of the Bloch space,then the closed graph theorem shows that there is a constant C>0 such that‖fg‖≤C‖g‖for all g∈B(BH).To check that f∈H∞(BH),it suffices to realize that and taking supremum for‖g‖≤1,we get|f(z)|‖δz‖≤‖δz‖C,thus|f(z)|≤C.That is,f∈H∞(BH). Since?(fg)(z)=f(z)?g(z)+g(z)?f(z),we get As mentioned above,for x,y∈BHwe have The growth of a function in B0(BH)behaves in the same way as in the finite dimensional case. Corollary 3.2The function f is a multiplier of the Bloch space B(BH)if and only if f is a multiplier of the little Bloch space B0(BH). Thus,fg∈B0(BH). For the converse,suppose that f is a multiplier of B0(BH).Then,there is C>0 such that‖fh‖≤C‖h‖for all h∈B0(BH).Let g∈B(BH).Using[3,Theorem 3.1],it suffices to prove that Consider,for 0 Letting r→1?,we obtain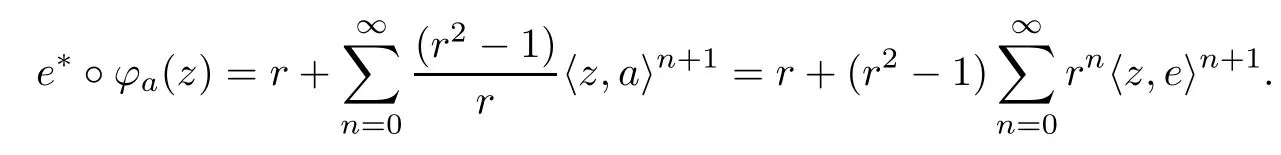
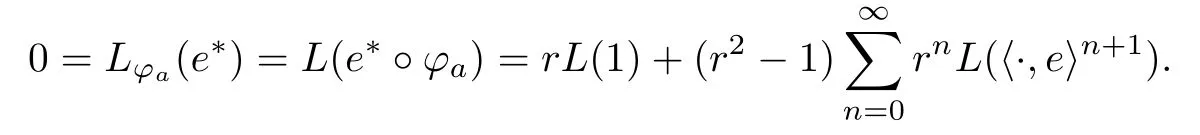


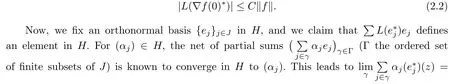
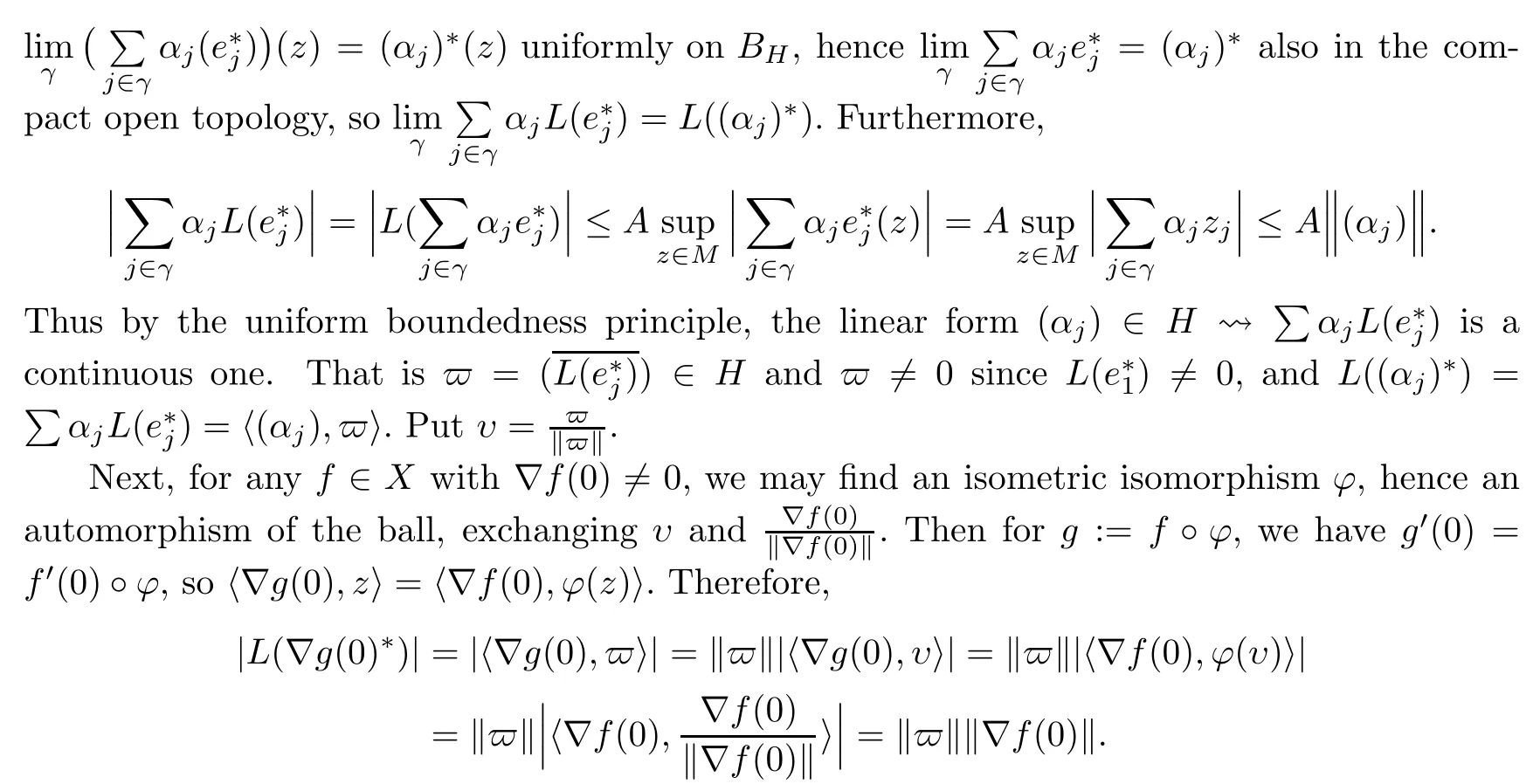

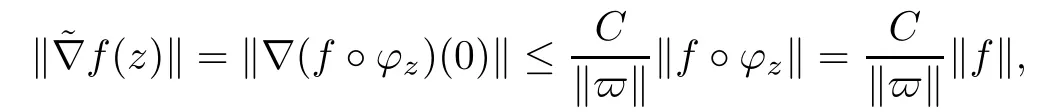
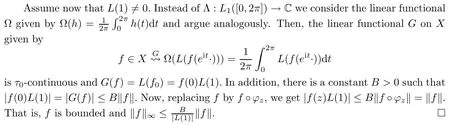
3 Multipliers
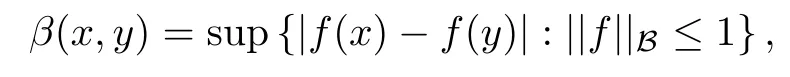
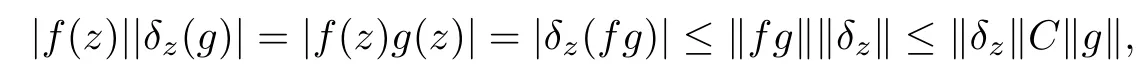
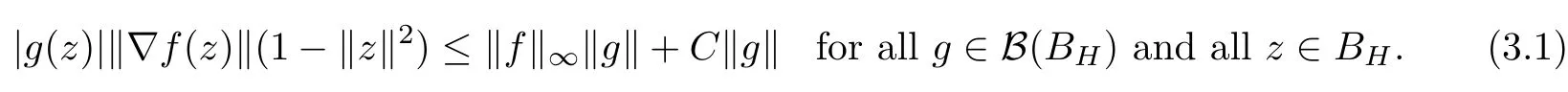

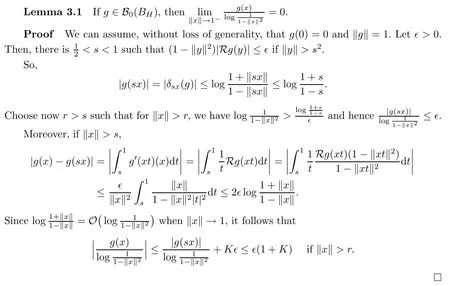

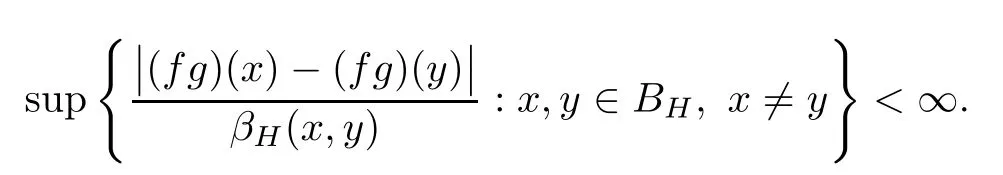
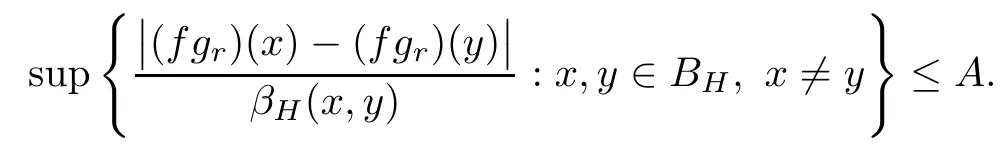


 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
