(田歌)

School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China

E-mail:tiang17@lzu.edu.cn

Haoyu WANG(王浩雨)

School of Information Science and Engineering,Lanzhou University,Lanzhou 730000,China

E-mail:2911828309@qq.com

Zhicheng WANG(王智誠)?

School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China

E-mail:wangzhch@lzu.edu.cn

Abstract This paper is concerned with the Fisher-KPP equation with diffusion and nonlocal delay.Firstly,we establish the global existence and uniform boundedness of solutions to the Cauchy problem.Then,we establish the spreading speed for the solutions with compactly supported initial data.Finally,we investigate the long time behavior of solutions by numerical simulations.

Key words Spreading speed;Fisher-KPP equation;diffusion;nonlocal delays

1 Introduction

The purpose of this paper is to study the long-time behaviors of solutions with compactly supported initial data for the following Fisher-KPP equation with diffusion and nonlocal delay:

Here the constantμ>0 represents the intrinsic growth rate of species.The convolution g?v,defined as

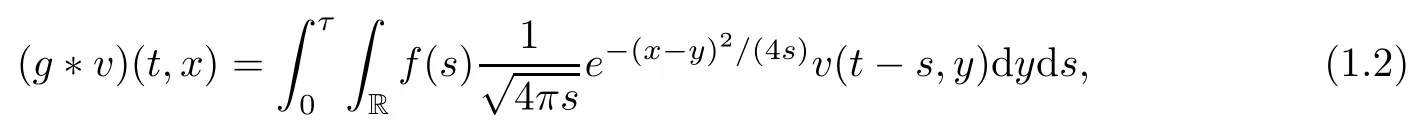
describes the nonlocal intraspecific competition for resources and accounts for the fact that individuals have not necessarily been at the same point in space at previous times.Such a delay formulated by the convolution is usually called a spatiotemporal delay or a nonlocal delay.Here f(·)is a nonnegative and integrable function on[0,τ]and satisfiesf(s)ds=1.For more details on spatiotemporal delays and nonlocal delays,we refer to Britton[1],Gourley and Britton[2],Gourley and Chaplain[3],Gourley and Ruan[4],Gourley,So and Wu[5],Gourley and Wu[6],Tian and Wang[7],Zou and Wu[8],and the references therein.

The long-time behaviors of solutions of reaction-diffusion equations with compactly supported initial data can describe very well the propagation phenomenon in population invasion and epidemic spread.Usually,such a propagation phenomenon can be characterized by investigating the so-called spreading speed of solutions.Thus far,there has been much research about the spreading speed of solutions with compactly supported initial data for when the solution semiflow is monotone.In particular,the theory about the spreading speed of the monotone semiflow can be applied to a reaction-diffusion system with nonlocal delay if the system is quasi-monotone[9–11].Unfortunately,equation(1.1)is not quasi-monotone.In fact,there are very few results about the spreading speed if the system is non-quasi-monotone(such as(1.1)).Hamel and Ryzhik[12]established the spreading speed for a nonlocal Fisher-KPP equation.The spreading speed for a kind of delayed Fisher-KPP equation was studied by Lin[13]and Liu and Pan[14].In this paper,we aim to investigate the spreading speed for(1.3)with a nonlocal delay.Note that the uniform boundedness of the solution is the key to proving the asymptotic behavior,however,we cannot obtain the uniform boundedness of the solution of(1.3)by the method of Hamel and Ryzhik[12]due to the delay.Meanwhile,the instantaneous self-limitation effect can dominate the corresponding delayed effect[13,14],but equation(1.3)does not have this property.Here we apply the explicit formula of the kernel g(t,x)and the comparison principle to deal with this issue.Based on the uniform boundedness of solutions,we can then establish the spreading speed of equation(1.1)by using an argument similar to that of Hamel and Ryzhik[12].Nevertheless,we would like to mention that traveling wave solutions of Fisher-KPP equations with diffusion and nonlocal delay have been widely studied[15–33].

Before stating the main results,we give some notations.Let X=BUC(R,R)be the Banach space of all bounded and uniformly continuous functions from R to R with the supremum norm‖·‖X.Let X+:={v∈X:v(x)≥0,x∈R}.Then X is a Banach lattice under the partial order induced by X+.It follows from Theorem 1.5 of Daners and Medina[34]that the X-realization ΔXof the Laplacian Δ generates a strongly continuous analytic semigroup Ψ(t)on X and Ψ(t)X+?X+for t≥0.In addition,we have that

Let C=C([?τ,0],X)be the Banach space of continuous functions from[?τ,0]into X with the supremum norm and let C+={?∈C:?(s)∈X+,s∈[?τ,0]}.Then C+is a positive cone of C.Usually,we identify an element ?∈C as a function from[?τ,0]×R into R defined by ?(s,x)=?(s)(x).For any continuous function w:[?τ,b)→X,b>0,we define wt∈C,t∈[0,b)by wt(s)=w(t+s),s∈[?τ,0].Thenis a continuous function from[0,b)to C.For K>0,let C[0,K]={?∈C:?(s,x)∈[0,K],s∈[?τ,0],x∈R}.

In what follows,we consider the Cauchy problem

Define F:C→X by

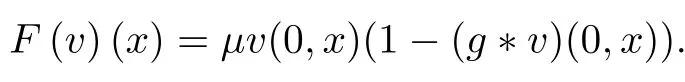
For integral equation

it is known that a mild solution of(1.3)is a continuous solution of(1.4);see Martin and Smith[35].The following theorem shows the global existence and boundedness of solutions of(1.3):

Theorem 1.1For any v0∈C+,equation(1.3)admits a unique mild solution v(t,x)=v(t)(x)∈C([?τ,∞),X)satisfying

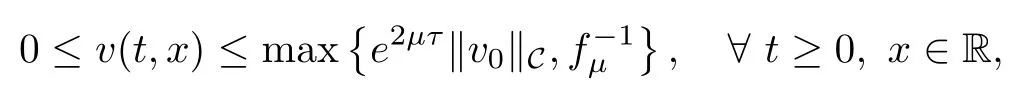
Based on the boundedness,we prove the spreading speed of solutions of(1.3)with compactly supported initial data.

Theorem 1.2Let v(t,x)be the solution of the Cauchy problem(1.3)with an initial condition v0∈C+such that v0(0,x)/≡0.Then

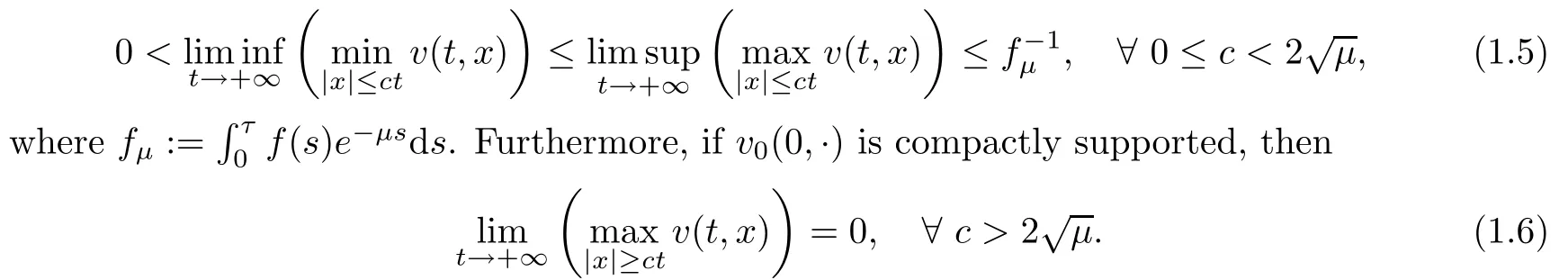
It is obvious that Theorems 1.1 and 1.2 also hold if f(t)=δ(t?τ),where δ(·)is the dirac delta function.Our paper is organized as follows:in Section 2,we prove Theorem 1.1.In Section 3,we give the proof of Theorem 1.2.In Section 4,we present the numerical simulations.

2 Global Existence and Uniform Boundedness

In this section we give the proof of Theorem 1.1.

Proof of Theorem 1.1We first show the local existence of solutions of(1.3)by using Banach’s fixed point theorem.Fix v0∈C+.Let K>eμτ.For T>0,define a set ΣTas follows:

For any v1,v2∈ΣT,define

It is clear that(ΣT,d(·,·))is a complete matrix space.Define a map F:ΣT→C([?τ,T],X)by

where v∈ΣTand vr(s,x)=v(r+s,x)for s∈[?τ,0]and x∈R.Then a fixed point of the map F on ΣTis a mild solution of(1.3)on[0,T].It is not difficult to show that F is Lipschitz continuous on ΣT.In particular,we can easily show the following two conclusions:

(1)For sufficiently small T>0,F(ΣT)?ΣT;

(2)For sufficiently small T>0,F:ΣT→ΣTis a contraction map.

Now take T>0 small enough.It follows from Banach’s fixed point theorem that there exists a unique function v(t,x)∈ΣT,which is the fixed point of the map F.Thus,v(t,x)∈ΣTis the unique mild solution of(1.3)on t∈[0,T]and satisfies

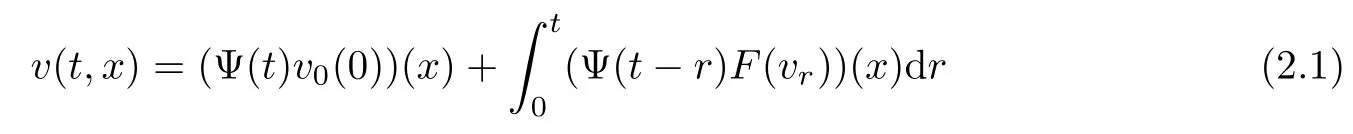
for t∈[0,T]and x∈R.This confirms the local existence of mild solution v(t,x)of(1.3).To establish the global existence of mild solution v(t,x)of(1.3),we can assume that v(t,x)is the unique non-continuable mild solution of(1.3)with the maximal interval of existencefor>0.Clearly,v(t,x)∈C(),X).Now we show

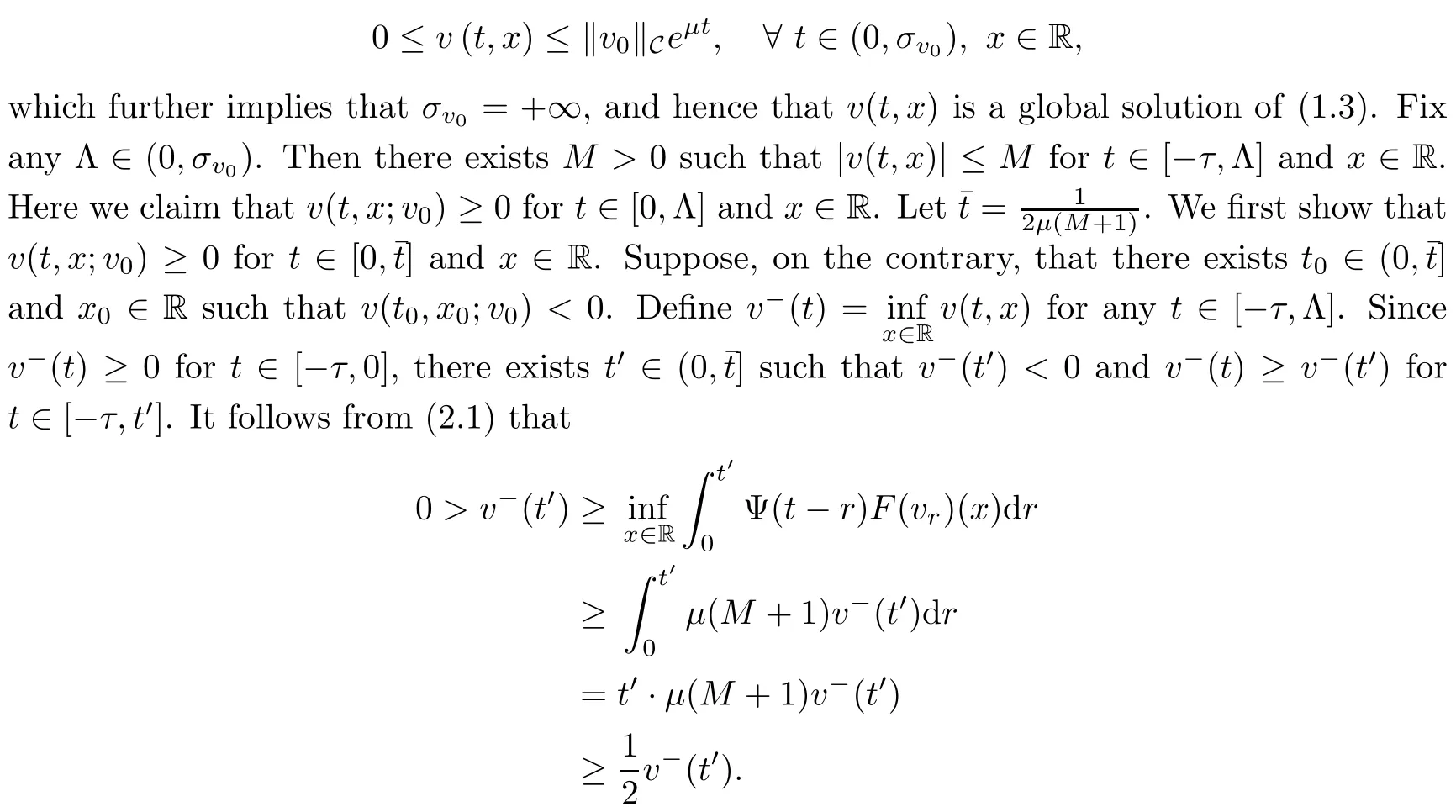
Clearly,there is a contradiction.Thus,we can confirm that v(t,x)≥0 for t∈[0,]and x∈R.By the properties of the semigroup Ψ(t),for any t>,we have

by which we can repeat the above discussion on intervals[k,(k+1)](k=1,2,...)and finally obtain that v(t,x)≥0 for t∈[0,Λ]and x∈R.By the arbitrariness of Λ>0,we obtain that v(t,x)≥0 for t∈[0,σv0)and x∈R.Now we show that v(t,x)≤‖v0‖Ceμtfor t∈(0,σv0)and x∈R.Following from(2.1),we have that

This completes the proof. □

3 Spreading Speed for the Cauchy Problem(1.3)

In this section,we will give the proof of Theorem 1.2,which is the spreading speed for the solution of equation(1.3).

Proof of Theorem 1.2We complete the proof by two steps.

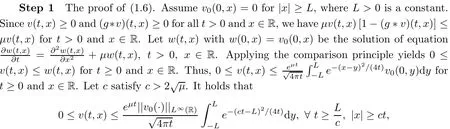
which immediately indicates that(1.6)holds;see[12,37].

Step 2The proof of(1.5).Firstly,we prove

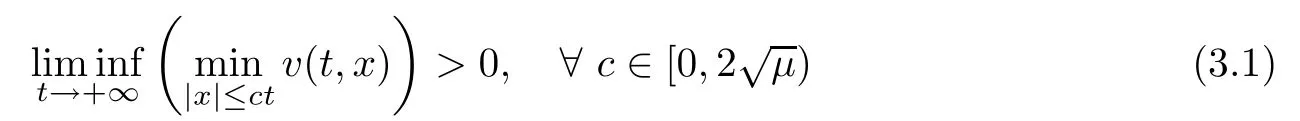
by contradiction.As v(t,x)≥0,for c∈[0,2√μ),we can choose sequences(tm)m∈Nand(xm)m∈Nin(tm,xm)∈(0,+∞)×R such that|xm|≤ctm,?m∈N and

By the boundedness of(||vm||L∞((?tm?τ,+∞)×R))m∈Nin Theorem 1.1,up to the extraction of some subsequence,we know that

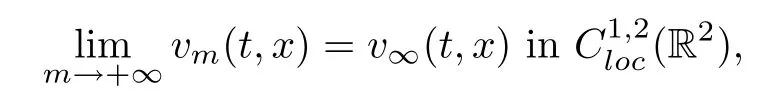
where v∞(t,x)satisfies

Fix σ>0 and L>0 satisfying that

respectively.By the strong parabolic maximum principle,there exists η>0 such that

In addition,it follows from(3.4)and(3.6)that

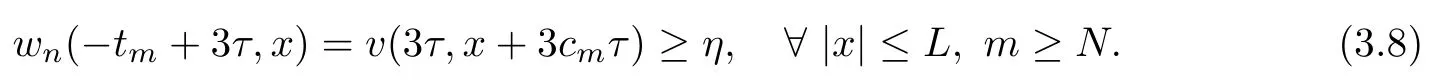
Now,by the continuity of g?wmon(?tm,+∞)×R and the minimality ofaccording to its definition,from(3.7)and(3.8),there holds one of the following two cases:

If the case(ii)holds,then(3.9)is obvious.However,when case(i)holds,it is not clear whetherhas a positive lower bound.Therefore,we only need to consider case(i).We use a contradiction argument.Suppose that case(i)holds and that(3.9)is not true.Then,up to the extraction of a subsequence,there exists a sequence(xm)m≥Nin[?L,L]such that

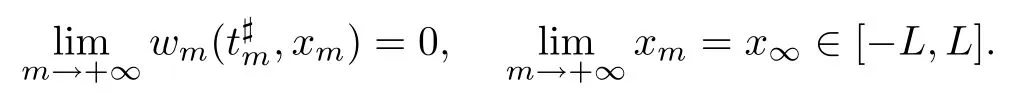
Define

It follows from(3.4)that wm(t,x)is the solution of

where(t,x)∈(?tm,+∞)×R.Thus,zm(t,x)also satisfies(3.10)for(t,x)∈[?tm?t?m,+∞)×R.

For any m≥N,since

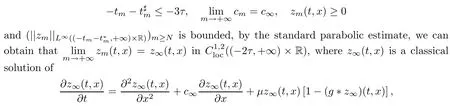
where(t,x)∈(?2τ,+∞)×R.In particular,

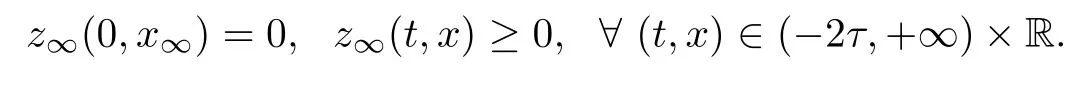
Therefore,by the strong maximum principle and the uniqueness of solutions of the Cauchy problem,we get

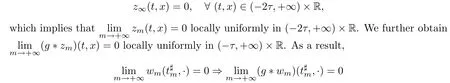
locally uniformly in R.Clearly,this contradicts case(i).Thus,(3.9)holds.

Combining(3.9)and(3.10),for every m≥N,we have that wm(t,x)satisfies

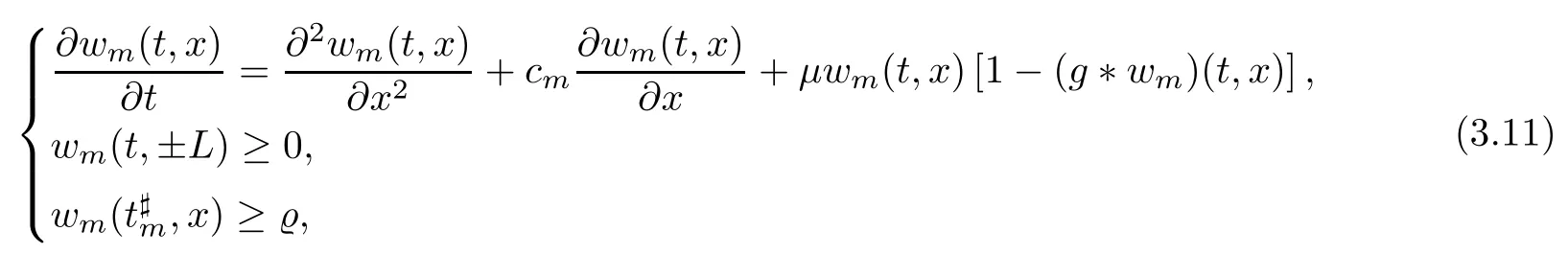
which indicates that ?m(x)is a lower solution of(3.11).By the parabolic maximum principle,for any m≥N,there is

From(3.3)and(3.4),we further have that

This contradicts(3.2).Thus,(3.1)holds.

which implies that(g?v)(t,x)≥fμv(t,x)for t>2τ and x∈R.By this inequality,we obtain

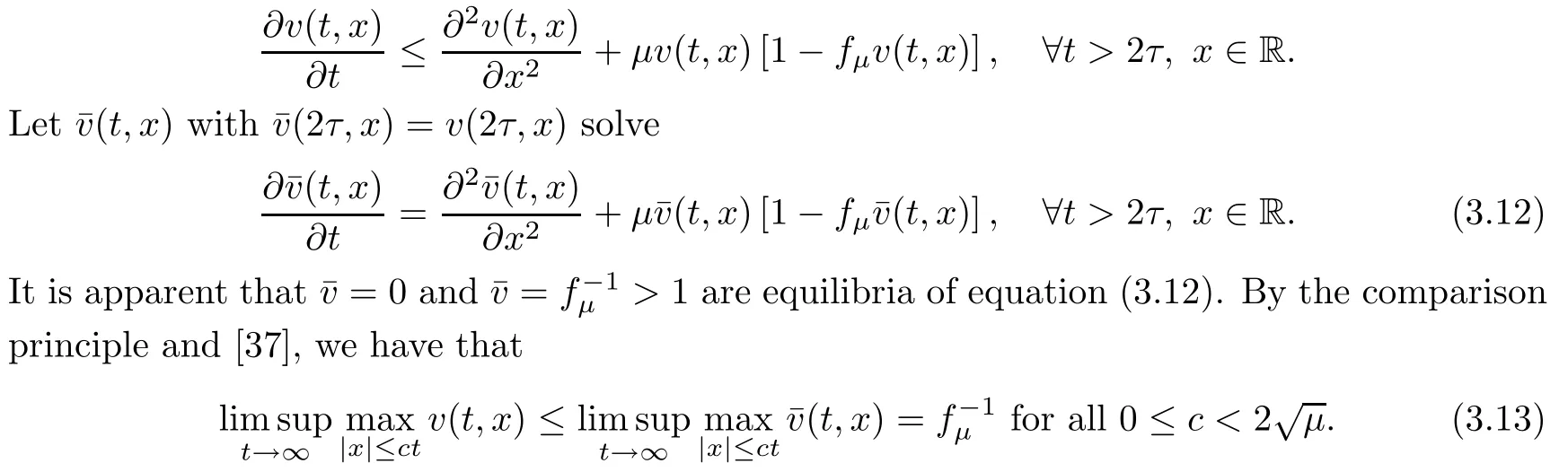
Finally,combining(3.1)and(3.13),we obtain(1.5). □

4 Numerical Simulations

Thus far,we have proved the global existence,boundedness and spreading speed of solutions with compactly supported initial data for the Cauchy problem(1.3).In this section,we continue to explore the long-time behaviors of solutions of(1.3)by numerical simulations.

For equation(1.3),we chooseμ=1,f(t)=δ(t?τ),that is,equation(1.3)reduces to

where t≥0,x∈R.To investigate this system by numerical simulation,we consider the case of a finite spatial domain with a homogeneous Neumann boundary condition,which models a closed environment with reflecting boundaries,that is,individuals cannot leave the domain.It is known that the nonlocal kernel

see[38–40].By calculation,we get that

In particular,G(x,y,t)>0 for t>0,x,y∈R.On this basis,system(4.1)can be approximated by the following initial boundary value problem on bounded domains(here we choose x∈[?100,100]:=? and t∈[0,200]):

In addition,from the composite Simpson’s rule,we have that

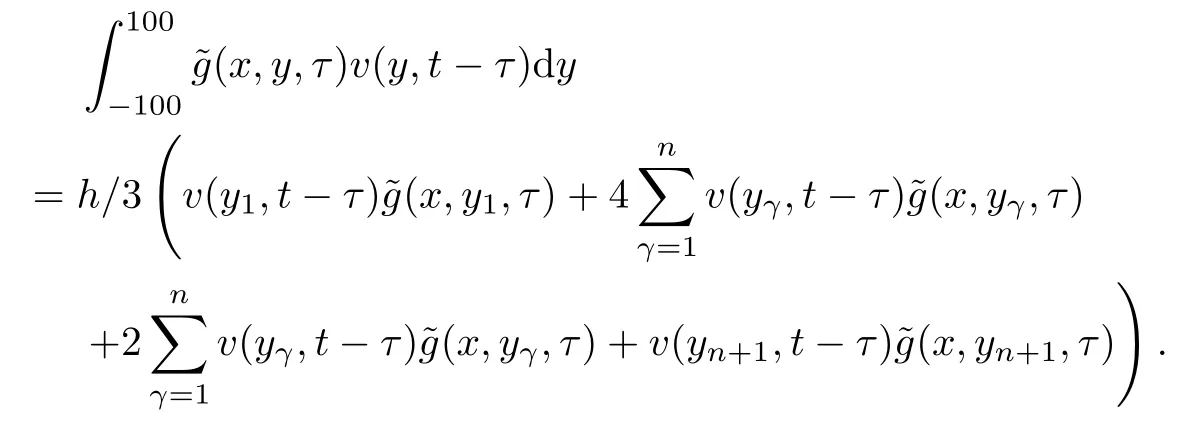
We then use the finite difference method to discretize(4.2).Define the uniform partition of domain ?=[?100,100]by

where h=200/n=0.2 and xi=x1+(i?1)·h,i=1,2,...,n+1.The time domain[0,200]is treated as k=200/m=0.02,tj=t1+(j?1)·k,j=1,2,...,n+1.

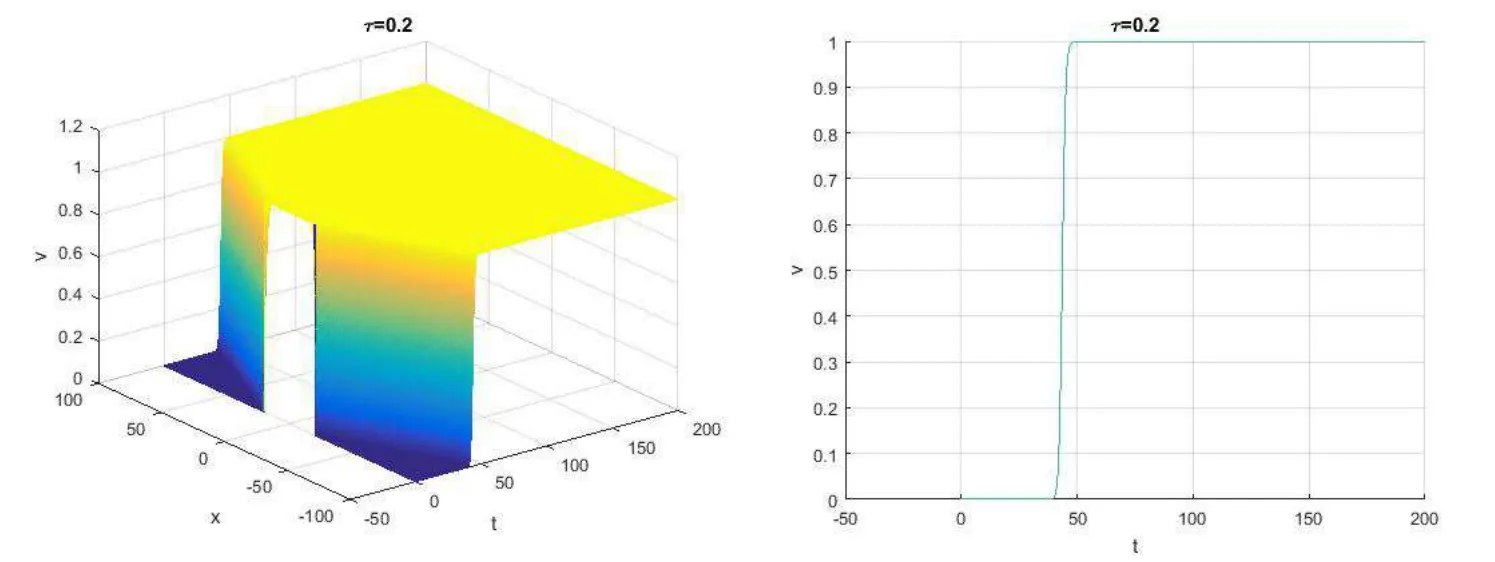
Figure 1 Choose α=20,τ=0.2.The left is a 3D-graph of v(t,x)and the right is a 2D-graph of v(t,x)at x=100

Figure 2 Choose α=20,τ=1.48.The left is a 3D-graph of v(t,x)and the right is a 2D-graph of v(t,x)at x=100

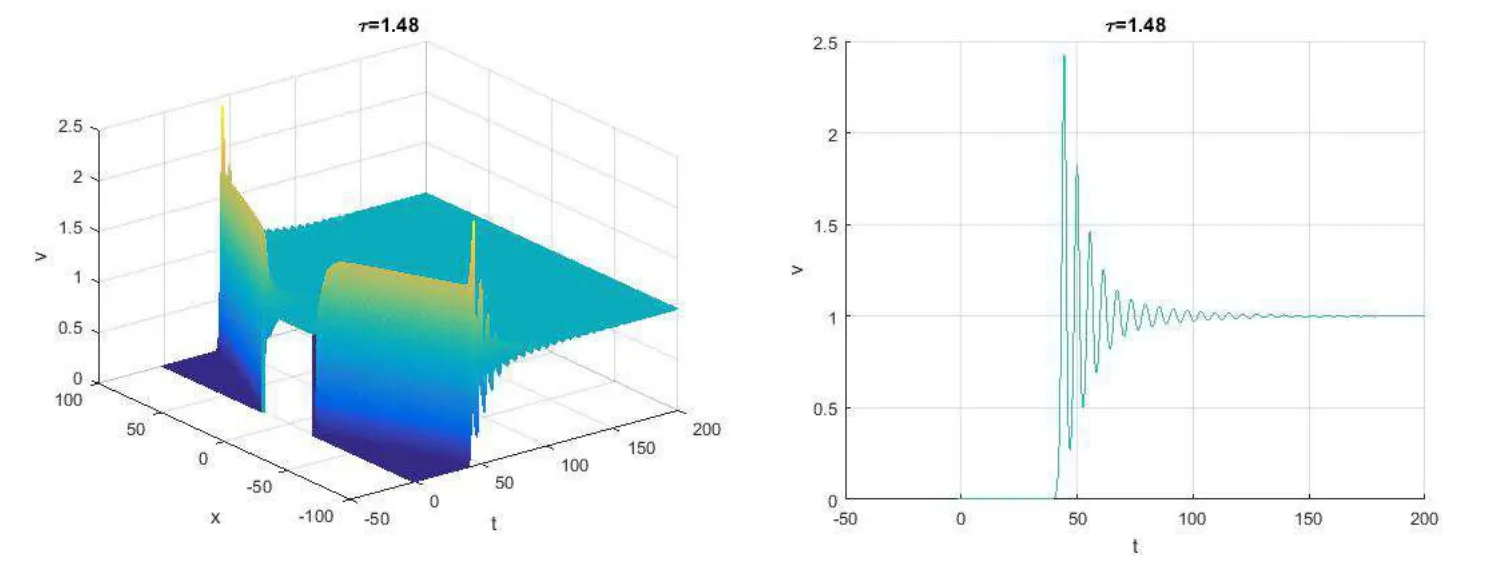
Figure 2 Choose α=20,τ=1.6.The left is a 3D-graph of v(t,x)and the right is a 2D-graph of v(t,x)at x=100

The numerical simulations show the large time behaviors of solutions of(4.1).From the figures,we see that,as time increases,for the small delay τ>0,the nonnegative steady states for(4.1)are v≡0 and v≡1;for sufficiently large τ>0,the steady state v≡1 becomes unstable and the non-constant bounded steady states may exist.In particular,if we choose τ=0.2 and τ=1.48,the solution finally connects 0 to 1.When choosing τ=1.6,as time increases,there exists an oscillating solution,but the solution still has upper and lower bounds and it seems to be a spatially uniform and temporally periodic solution.Britton[1]investigated the spatial structure of system(4.1)when the initial condition is given by v0(s,x)=1,and showed that there exists a bifurcation to time periodic solution when τ=.By a series of calculations as Britton[1],we get that when τ<,the roots of the characteristic equation at the equilibrium v=1 have negative real parts and v=1 is stable.On the other hand,when τ>,there exist positive real parts and v=1 is unstable,which is consistent with the results of our numerical simulations.

Furthermore,in all cases,we observe that the spreading speed of solution of(4.1)is approximately equal to 2,which confirms the conclusion of Theorem 1.2.