ENTANGLEMENT WITNESSES CONSTRUCTED BY PERMUTATION PAIRS?
(候晉川) (王文麗)
School of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
E-mail:jinchuanhou@aliyun.com;995929733@qq.com
Abstract For n≥3,we construct a class of n2×n2 hermitian matrices by the permutation pairs and show that,for a pair{π1,π2}of permutations on(1,2,...,n), is an entanglement witness of the n?n system if{π1,π2}has the property(C).Recall that a pair{π1,π2}of permutations of(1,2,...,n)has the property(C)if,for each i,one can obtain a permutation of(1,...,i?1,i+1,...,n)from(π1(1),...,π1(i?1),π1(i+1),...,π1(n))and(π2(1),...,π2(i?1),π2(i+1),...,π2(n)).We further prove that is not comparable with Wn,π,which is the entanglement witness constructed from a single permutation π; is decomposable if π1π2=id or =id.For the low dimensional cases n∈{3,4},we give a sufficient and necessary condition on π1,π2 for to be an entanglement witness.We also show that,for n∈{3,4}, is decomposable if and only if π1π2=id or =id; is optimal if and only if(π1,π2)=(π,π2),where π=(2,3,1).As applications,some entanglement criteria for states and some decomposability criteria for positive maps are established.
Key words Separable states;entangled states;positive maps;entanglement witnesses;permutations
1 Introduction
The phenomenon of entanglement is of fundamental interest,since it is the main difference between the classical and quantum worlds.Furthermore,entanglement is a central resource for quantum computation and protecting quantum communication.However,recognizing entanglement in the quantum states of composite systems is a basic but difficult task in quantum information theory.Many entanglement criteria have been established both for finite-dimensional and infinite-dimensional systems in recent years,though the problem of detecting entanglement is still not solved satisfactorily(see[1,3–6,9,15,16,23,24,27]).
Mathematically,a quantum system may be described by a separable complex Hilbert space H,and every quantum state(or density matrix,or density operator)of this system is a positive operator acting on the state space H with trace 1.Denote by S(H)the set of all states on H.Clearly,the set S(H)is convex and closed under trace-norm topology.For n≥2,an n-partite composite system is described by a tensor product space H=H1?H2?...?Hn.Let ρ be a quantum state in a bipartite system described by Hilbert space H?K with dimH?K≤∞.ρ is said to be separable if ρ∈‖·‖1?co{P?Q:P∈P1(H),Q∈P1(K)},where‖·‖1?co(L)stands for the closed convex hull of the subset L in the trace-class operator space T(H?K)under trace norm topology,and P1(H)is the set of all pure states(that is,rank-1 projections)in H.Otherwise,ρ is called an entangled state.Recall that a self-adjoint operator W∈B(H?K),the von Neumann algebra of all bounded linear operators acting on H?K,is called an entanglement witness(for brevity,EW),and is denoted by W∈EW(H?K)if W is non-positive and Tr(W(P?Q))≥0 holds for all P∈P1(H)and Q∈P1(K).The entanglement witness criterion is a necessary and sufficient criteria of entanglement detection which asserts that a bipartite state ρ in system H?K is entangled if and only if there exists some entanglement witness W∈EW(H?K)such that Tr(Wρ)<0([2,5–7,24]).The entanglement witness criterion gives rise to a practical and experimentally accessible test for entanglement.However,though every entangled state can be recognized by some EW,there is no universal EW by which all entangled states can be detected,and describing all entanglement witnesses is NP hard.A solution to this problem may be to establish a database of tangible entanglement witnesses for any dimension which is big enough,so that we can enlarge the database via machine learning and,for a given entangled state,we can first try to find a suitable entanglement witness in the database to detect it.Thus,it is worth finding as many new classes of tangible entanglement witnesses as possible and enlarging the stock of known entanglement witnesses.This is why the construction and the properties of entanglement witnesses have been studied intensively by many authors(See,for instance,[8,9,11,12,18,20,21,25,27]and the references therein).
Denote by B+(H?K)the convex cone of all positive operators acting on H?K and by conesep(H?K)the convex cone generated by all separable states.Generally speaking,every W∈EW is a bounded linear functional which is positive on conesep(H?K).In fact,we have
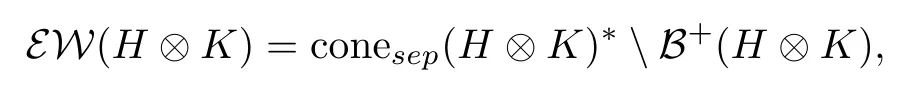
where conesep(H?K)?is the dual cone of conesep(H?K);that is,the convex cone of all bounded linear functionals of T(H?K)that are positive on conesep(H?K).Note that EW(H?K)is not convex(See[8,26]).
Much effort has gone into finding ways of constructing new entanglement witnesses.There is a way of constructing entanglement witnesses by non-identity permutations[18–21]).In the present paper,based on the work on positive maps in[13],we propose a class of entanglement witnesses constructed by permutation pairs,and discuss their properties.
The paper is organized as follows:in Section 2 we propose a method for constructing Hermitian matricesof the n?n system by any permutation pair{π1,π2}and show that such ais an entanglement witness if{π1,π2}has the property(C),which will be described later.In Section 3,we compare the class of EWsin the previous section with the EWs Wn,πconstructed by single permutations and show that these two classes are not comparable to each other except for a trivial special case,which means thatcan detect entangled states that Wn,πcannot.Section 4 is devoted to discussing decomposability and showing that the EW constructed by a permutation pair{π1,π2}with the property(C)is decomposable if eitheror π1π2=id.As an application,in Section 5 we illustrate how to use this new class of EW to detect entanglement in a quantum state.Note that{π1,π2}having the property(C)is only a sufficient condition for ensuring thatis an entanglement witness.We still do not know the necessary and sufficient conditions on{π1,π2}for thebeing an entanglement witness.In Section 6 we consider the low dimensional cases;that is,the 3?3 system and the 4?4 system.In these low dimensional cases we can obtain necessary and sufficient conditions for a Hermitian matrixconstructed by a permutation pair to be an entanglement witness of the n?n system with n=3 or 4.We also show that,for the 3?3 and 4?4 systems,an EWis decomposable if and only if either=id or π1π2=id;for the 3?3 system,an EWconstructed by permutation pair{π1,π2}is optimal if and only if π1=(2,3,1)and π2=(3,1,2).As corollaries,we get conditions for the positive maps on Mnconstructed by a permutation pair in[13,28]to be decomposable,where Mn=Mn(C)stands for,as usual,the algebra of all n×n matrices over the complex field C.
2 Constructing Entanglement Witnesses by Permutation Pairs
We need a lemma from[21],though here we give a direct and different proof.

If we take|x〉so that ξ1=ξ2=...=ξn/=0,then the above equation reveals that<0 as ti?n+1≤0 and t1?n+1<0. Hence,is not positive semi-definite.
Statement(2)is a part of the assertion of[22,Proposition 2.6]. □
Consider an n?n bipartite system Cn?Cn.Letbe an orthonormal basis of Cn.Denote by Eklthe rank-1 operator|k〉〈l|for k,l∈{1,2,...,n}.Thus Eklmay be regarded as the matrix with(k,l)-entry 1 and other entries 0,and every state on Cn?Cnis a density matrix in Mn(C)?Mn(C).
Recall that a pair{π1,π2}of permutations of(1,2,...,n)is said to have the property(C)if,for any given i∈{1,2,...,n}and for any j/=i,there exists πhj(j)∈{π1(j),π2(j)}with hj∈{1,2}such that the map σ defined by σ(j)=πhj(j),j=1,2,...,i?1,i+1,...,n,is a permutation of(1,2,...,i?1,i+1,...,n)(See[13]).Roughly speaking,a pair{π1,π2}of permutations of(1,2,...,n)has the property(C)if,for each i,one can obtain a permutation of(1,...,i?1,i+1,...,n)from(π1(1),...,π1(i?1),π1(i+1),...,π1(n))and(π2(1),...,π2(i?1),π2(i+1),...,π2(n)).For example,letting π be the permutation of(1,2,...,n)defined by π(i)=i+1 mod n,it is easily checked that,for any 1≤p≤n?1,{πp,πp+1}has the property(C);{π,π4}has the property(C)if n=5 and 7,but does not have the property(C)if n=6.
For a nonempty proper subset F of{1,2,...,n},we say that F is a(common)invariant subset of{π1,π2}if πh(F)=F holds for all h=1,2.Obviously,there exist disjoint minimal invariant subsets F1,F2,...,Flof{π1,π2}such thatn;herestands for the cardinality of the set G.Such a collection{F1,F2,...,Fl}is called the complete set of minimal invariant subsets of{π1,π2}.Thus one can reduce the pair{π1,π2}of permutations into l pairsof small ones,whereh=1,2.It is easily checked that{π1,π2}has the property(C)if and only if each pairof the sub-permutations has the property(C).Therefore,to check whether or not{π1,π2}have the property(C),we may assume that π1and π2have no common proper invariant subsets and that n≥2.
The following two results can be found in[13]:
Lemma 2.2Let n≥2 and let π1,π2be two permutations of(1,2,...,n)having no proper common invariant subsets.Then{π1,π2}has the property(C)if and only if the following conditions are satisfied:
(1)For any distinguished i,j,π1(i)/=π2(i)and{π1(i),π2(i)}/={π1(j),π2(j)};
(2)For any i and j1,j2with π1(j2)=π2(j1)=i,if distinct j3,...,jm/∈{i,j1,j2}satisfy that π2(j3)=π1(j1),π2(j4)=π1(j3),...,π2(jm)=π1(jm?1),then π1(jm)/=π2(j2).
Suppose that ΦD:Mn→Mnis a linear map of the form
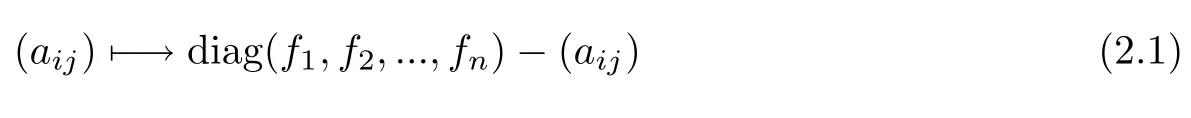
with(f1,f2,...,fn)=(a11,a22,...,ann)D for a given n×n nonnegative entry matrix D=(dij)(that is,dij≥0 for all i,j).The map ΦDof the form Equation(2.1)defined by a nonnegative entry matrix D is called a D-type map(see[10]).
Assume that π is a permutation of(1,2,...,n).Recall that the permutation matrix Pπ=(pij)of π is an n×n matrix determined by
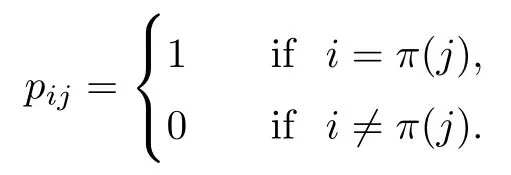
Lemma 2.3For any two permutations π1and π2of(1,2,...,n)with n≥3,letMn→Mnbe the D-type map of the form
where(f1,f2,...,fn)=(a11,a22,...,ann)D and D=(n?2)In+Pπ1+Pπ2with Pπhthe permutation matrix of πh,h=1,2.If{π1,π2}has the property(C),thenis positive.
The following is the main result of this section,and it proposes a class of entanglement witnesses constructed by permutation pairs:
Theorem 2.4Let π1,π2be two permutations of(1,2,...,n)with n≥2.If at least one of π1and π2is not the identity,and if the pair{π1,π2}has the property(C),then
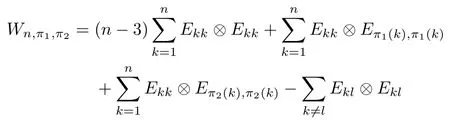
is an entanglement witness of the n?n system.
ProofWe prove the theorem by considering two cases.
Case 1One of π1,π2is the identity.
With no loss of generality,say that π1=id.Then
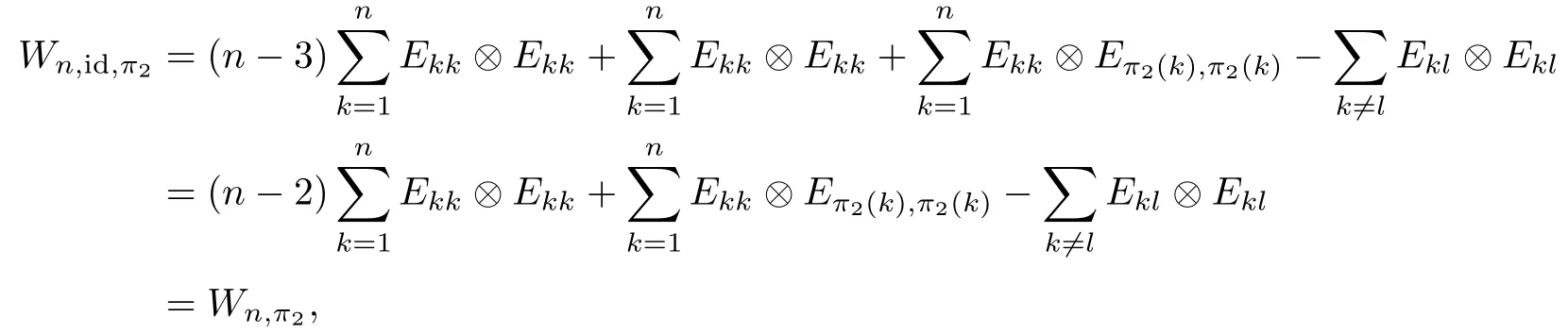
which is in fact an entanglement witness constructed from a single permutation π2(see[17]).
Case 2Neither π1nor π2is the identity.
In this case we must have that n≥3.As the pair{π1,π2}has the property(C),by[13],the D-type map=ΦD:Mn(C)→Mn(C)constructed from the permutation pair{π1,π2}is a positive map.Here D=(n?2)I+with Pπbeing the permutation matrix associated to the permutation π.Thus,it follows that the Choi-Jamiokowski matrixis an entanglement witness whenever it is not positive;see,for instance,[18].
It is not difficult to check that,for any A∈Mn(C),
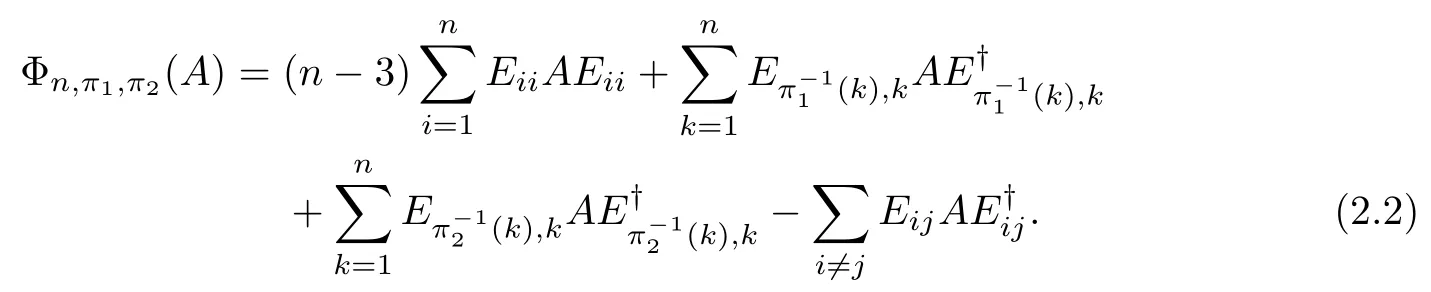
Thus we have

It follows that

Corollary 2.5For n≥2,let{π1,π2}be a pair of permutations of(1,2,...,n).Then the D-type map:Mn(C)→Mn(C)is completely positive if and only if{π1,π2}={id,id}.
We remark that in the above corollary,we do not require that the pair{π1,π2}has the property(C).
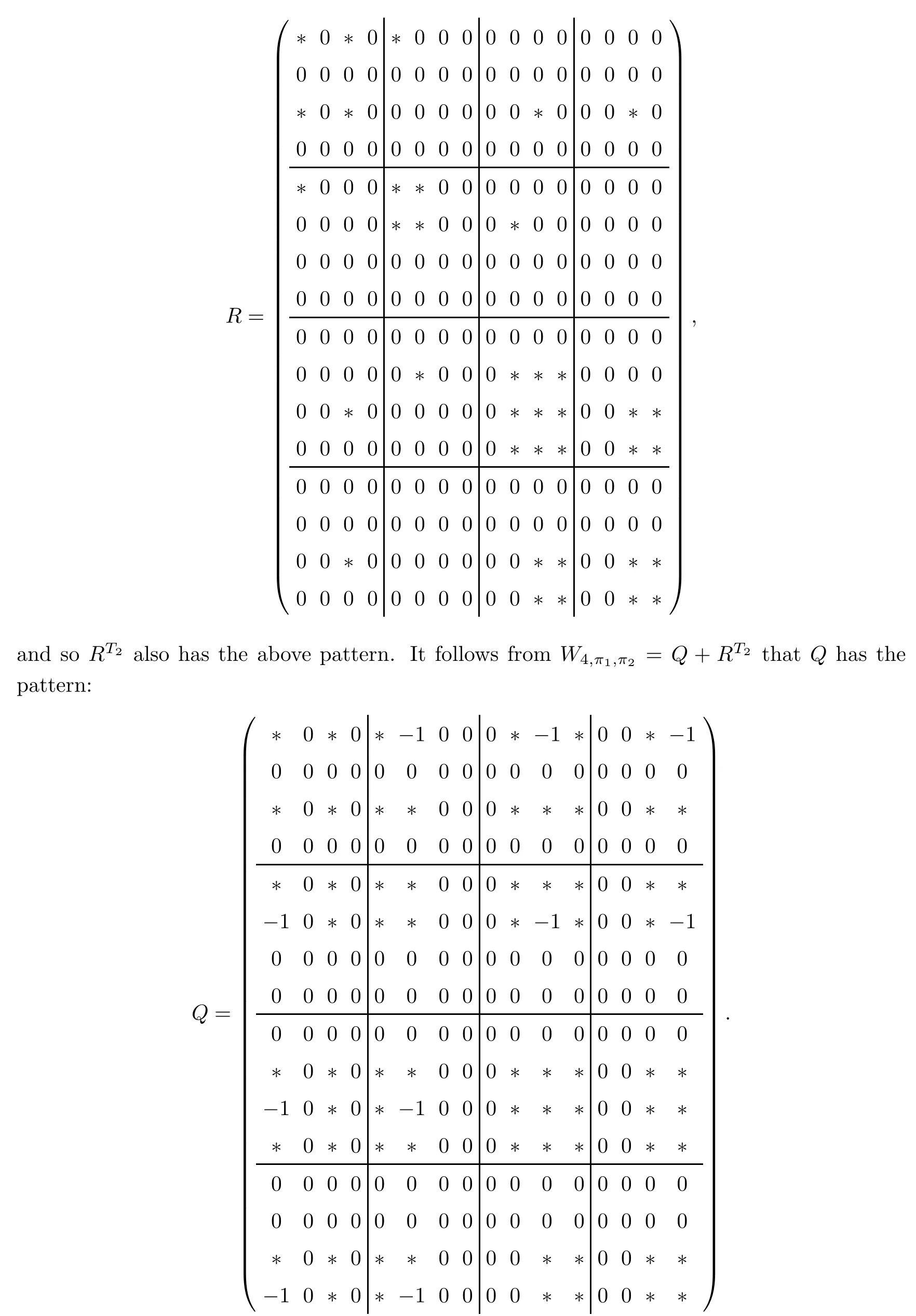
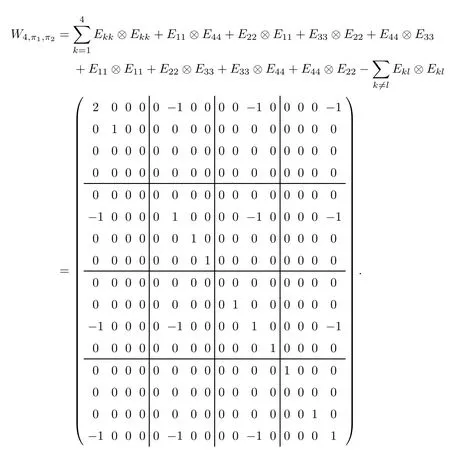
Corollary 2.6Let n≥3 and π be the cyclical permutation defined by π(i)=i+1 mod n.For 1≤p (i)q?p=1; (ii)1 (iii)1 Then is an entanglement witness of the n?n system.Here k+p is identified with k+p mod n. ProofBy[13],the pair{π1,π2}={πp,πq}has the property(C)if and only if(p,q)satisfies one of the conditions(i),(ii)or(iii).Note that neither πpnor πqis the identity permutation,and that π1(k)=k+p mod n,π2(k)=k+q mod n.Simply denote π1(k)=k+p.Then,by Theorem 2.4, is an entanglement witness. □ Theorem 2.4 can be generalized to any bipartite composite system by using a method from[17]. Then,by Theorem 2.4,the finite rank operator for every A∈B(H)is NCP positive,too.Then, is a finite rank entanglement witness of system H?K.Thus,for any permutation pair{π1,π2}with the property(C),we obtain a class of entanglement witnesses where U(H)is the group of all unitary operators on H. In particular,for permutations σ1,σ2of(1,2,...,n),if U and V are the unitary operators defined by U?|i〉=|σ2(i)〉,V|i〉=|σ1(i)〉for i=1,2,...,n and U?|i〉=|i〉,V|i〉=|i〉for i>n,then,by Equation(2.3),it is easily checked that for every A∈B(H).Correspondingly,by Equation(2.4),we get an entanglement witness of the form Applying Equation(2.5)gives that if 1≤i/=j≤n,and if 1≤i≤n.Now,substituting Equations(2.7)–(2.8)into Equation(2.6)yields that which is clearly the same as that which is given in the theorem. □ In this section,we show that the entanglement witnesses constructed by permutation pairs in the previous section provide a new class of entanglement witnesses different to the entanglement witnesses constructed by single permutations.To do this,let us recall some notions and notations. Consider a bipartite quantum system H?K.For an entanglement witness W∈EW(H?K),denote by DW={ρ:ρ∈S(H?K)with Tr(Wρ)<0}the set of all entangled states that can be recognized by W.Let W1and W2be two entanglement witnesses.We say that W2is finer than W1,denoted bywe say that W1and W2are comparable if eitherwe say that W1and W2are equivalent,denoted by W1≈W2,if(see[8,26]).Obviously,if W1and W2are not comparable,then there are entangled states ρ1and ρ2so thati,j∈{1,2}with i/=j,which means that W1can recognize some entangled states that W2cannot,while W2can recognize some other entangled states that W1cannot.Thus,if W1and W2are not comparable,then neither can be replaced by the other as a tool of entanglement detection. For any non-identity permutation π of(1,2,...,n),in[20],an entanglement witness Wn,πwas constructed as and its properties were discussed in[18–21].We shall show that almost all entanglement witnessesconstructed by permutation pairs are not comparable to any entanglement witnesses Wn,πconstructed by single permutation. Theorem 3.1Let π1,π2,π be any non-identity permutations of(1,2,...,n)(n≥3)with{π1,π2}having the property(C).Then the following statements are equivalent: As(Eii?Ejj)D1(Eii?Ejj)≥0,we see that d≤1 and,for any k=1,2,...,n,{π1(k),π2(k)}?{k,π(k)}. Assume firstly that π1and π2have no proper common invariant subset.As{π1,π2}has the property(C),by Lemma 2.2,π1(k)/=π2(k),and consequently,{π1(k),π2(k)}={k,π(k)}with π(k)/=k for each k.Denote by Jithe set of all fixed points of πi,i=1,2.Then,Ji/=?,J1∩J2=?and J1∪J2={1,2,...,n},so Jis are proper common invariant subsets of π1and π2,which is a contradiction.This means that π1,π2must have proper common invariant subsets. Let{F1,F2,...,Fl}be the complete set of minimal invariant subsets of{π1,π2},and denotei=1,2.Then l≥2.For each 1≤s≤l,the pair{π1s,π2s}of permutations of Fshas the property(C)and has no proper common invariant subsets.This entails that{π1(k),π2(k)}={k,π(k)},and Fsis also an invariant subset of π for each s=1,2,...,l.However,if neither π1snor π2sis the identity on Fs,then an argument similar to the one above reveals that{π1s,π2s}has proper common invariant subsets,which contradicts the fact that Fsis a minimal invariant subset of{π1,π2}.Therefore,either π1sor π2sis the identity on Fs.LetAs neither π1nor π2is the identity,one sees that F/={1,2,...,n}andMoreover,the fact that{π1(k),π2(k)}={k,π(k)}entails that π(k)=π2(k)for k∈F and π(k)=π1(k)for k∈Fc.Thus(2)is true. Case 2If this is the case,then there exists some scalar t>0 and a positive semi-definite matrix D2≥0 such that W2=tW1+D2.Assume that W1is linearly independent of W2.Then D/=0.It follows that As(Eii?Ejj)D2(Eii?Ejj)≥0,we must have π(k)∈{k,π1(k),π2(k)}for each k.Thus, Let us calculate the value of rkfor each k=1,2,...,n.There are five situations. (a)π1(k)/=k,π2(k)/=k and π(k)/=k.In this situation,we have π(k)∈{π1(k),π2(k)}and rk=(n?3)?t(n?2); (b)π1(k)/=k,π2(k)/=k and π(k)=k.It is clear in this situation that rk=(n?3)?t(n?1); (c)πi(k)=k,πj(k)/=k,π(k)/=k,i,j=1,2,i/=j.In this case,we have π(k)=πj(k)and rk=(1?t)(n?2); (d)πi(k)=k,πj(k)/=k,π(k)=k,i,j=1,2,i/=j.This time we get rk=(n?2)?t(n?1); (f)π1(k)=π2(k)=k.In this case,we must have that π(k)=k,and thus rk=(1?t)(n?1).As rk≥0,one sees that t≤1. If t=1,then only the situations(c)and(f)may happen,but this will imply that all rks and cls are 0,which leads to D2=0,which is a contradiction.Hence t<1 and Then,it follows that This contradiction implies that W1is linearly dependent of W2;that is,W2=tW1for some t>0.Clearly,t=1 and hence W2=W1.Thus(3)is true. The proof is finished. □ Now the following result is obvious: Theorem 3.2Let π1,π2,π be any non-identity permutations of(1,2,...,n)(n≥3)with{π1,π2}having the property(C).If/=Wn,π,then the entanglement witnesses Wn,πandare not comparable. It is easily seen that both Q1and Q2are positive semi-definite.Since we have that Let and Obviously,both Q1and Q2are positive semi-definite and Now,assume that π1or π2have fixed points.Denote by Fithe set of all fixed points of πi,i=1,2.Then Let and If one of the permutations π1or π2is the identity,thenreduces to Wn,π,which was dealt with in[17–21].Thus,in this section,we assume that both π1and π2are not the identity,and consequently,that n≥3.For any state ρ∈Mn?Mn,ρ can be represented asαijklEij?Ekl.As ρ?=ρ,we have that (i)q?p=1; (ii)1 (iii)q?p≥2 but p=n?d(q?p)for some integer 1≤d≤m?1 whenever there are relatively prime positive integers k,m with m then ρ is entangled. ProofThis is obvious from Corollary 2.6 and Theorem 5.1. □ More generally,applying Theorem 2.7,we have then ρ is an entangled state. We now discuss the low dimension cases n≤4,which allow us to get the necessary and sufficient conditions forto be an entanglement witness without assuming that{π1,π2}has the property(C).We also show that,when n≤4,is decomposable if and only if either π1π2=id or=id(compared with Theorem 4.1). As the case n=2 is trivial,we consider two cases:the case n=3(in Subsection 6.1)and the case n=4(in Subsection 6.2). We first consider the case when n=3.The following result gives a necessary and sufficient condition forto be an entanglement witness: Theorem 6.1Let π1and π2be two distinct permutations of(1,2,3)that are not the identity,and let Recall that an entanglement witness is said to be optimal if for any entanglement witness W1,will imply W1≈W.It is well known that every entangled state can be detected by some optimal entanglement witness.In[19]it was shown that the EW W3,π,constructed by single permutation π of(1,2,3),is optimal if and only if π is cyclic;that is,l(π)=3.Howerver,for those introduced by permutation pair,there is only one that is optimal. To complete the proof,we have to show that W3,1,2is optimal.Obviously,W3,1,2=with It follows that Taking αi,βj∈R gives In particular,let αi=tβi,where|t|=1.Then Tr(W3,1,2(P1?P2))=0.Since Tr(W3,1,2?D)(P1?P2))≥0 and Tr(D(P1?P2))≥0,we must have that for some nonnegative numbers a,b,c∈[0,1].If D/=0,then at least one of a,b,c is nonzero.With no loss of generality,assume a>0.Then,with any product pure state P1?P2,as in Equation(6.1),we have By Equation(6.2),we get which contradicts the assumption that W3,1,2?D is an entanglement witness. Therefore,there is no nonzero positive semi-definite matrix D such that W3,1,2?D is still an entanglement witness;that is,W3,1,2is optimal. □ A positive map Φ:Mn→Mnis said to be optimal if,for any C∈Mn,the map XΦ(X)?CXC?is not positive.Clearly,completely positive maps are not optimal.It was shown in[18]that,for a NCP positive map Φ:Mn→Mn,the entanglement witness?Eijis optimal if and only if Φ is optimal.By Theorem 6.1 and Theorem 6.2 we have Corollary 6.3Every positive map:M2→M3constructed by permutation pair{π1,π2}is decomposable,andis an optimal positive map if and only if π1=(2,3,1)and π2=(3,1,2). For the case when n=4,we also can get a necessary and sufficient condition forto be an entanglement witness. Theorem 6.4Let π1and π2be two distinct permutations of(1,2,3,4)that are not the identity,and let (i)l(π1,π2)=2;or (ii)l(π1,π2)≥3 and the following two conditions hold: (1)if k is not the fixed point of both π1and π2,then π1(k)/=π2(k); (2)if π1and π2have no common fixed points and if there exist distinct h,k such that{π1(h),π2(h)}={π1(k),π2(k)},then neither π1nor π2has fixed points. Note that each possible choice of π2has two fixed points. Consider the case{π1,π2}={(2,3,1,4),(1,2,4,3)}.Then Hence R≥0 means that R has the pattern: As Q≥0,its principal submatrix which contradicts A≥0. The contradiction shows thatis indecomposable. The other situations are dealt with similarly,and the proof of Claim(a)is complete. Claim(b)If(l(π1),l(π2))=(3,3),then{π1,π2}does not meet the condition(ii)in Theorem 6.4,so this case does not occur. For instance,assume π1(4)=4. Then π1∈{(2,3,1,4),(3,1,2,4)}.If π1=(2,3,1,4),by the condition(ii)(1)of Theorem 6.4,it is obvious that π2has three possible choices: However,it is easily checked that no choice meets the condition(ii)(2)of Theorem 6.4.Similarly,if π1=(3,1,2,4),there is no π2with l(π2)=3 so that{π1,π2}meets the condition(ii)of Theorem 6.4.Hence the case(l(π1),l(π2))=(3,3)cannot occur. Claim(c)If(l(π1),l(π2))=(4,2),thenis indecomposable. As l(π1)=4,π1has six possible choices: If π1=(2,3,4,1),then π2has only one possible choice:π2=(3,4,1,2).Other possible choices of pair{π1,π2}are We claim that,for any one of the above six choices of{π1,π2},is indecomposable. For example,consider the choice{π1=(2,3,4,1),π2=(3,4,1,2)}.We have that is Thus R has the pattern: which has a principal submatrix As qkkkk≤1,we must have qkkkk=1 for k=1,2,3,4.Let α=q1313and β=q2424.Clearly,|α|≤1 and|β|≤1.Then,taking|x〉=(ξ,ξ,ξ,ξ)t∈R4,and considering〈x|A|x〉,gives that α+≥4,which entails that α=β=1.Therefore,rkkkk=0 for k=1,2,3,4 as qkkkk+rkkkk=1.It follows that and thus Note that R has a principal submatrix C with However,it is clear that D is not positive semi-definite,which is a contradiction. Claim(d)If(l(π1),l(π2))=(4,3),thenis indecomposable. Obviously,π1=(2,3,4,1)implies that π2∈{(3,1,2,4),(4,1,3,2),(4,2,1,3),(1,4,2,3)},and π1=(4,1,2,3)implies that π2∈{(1,3,4,2),(3,2,4,1),(2,4,3,1),(2,3,1,4)}.As π1has six possible choices,there are 24 situations to be dealt with in this case. Take,for example,π1=(4,1,2,3),π2={(1,3,4,2).Then If there exist positive semi-definite matrices Q,R so thatthen Q,R have the pattern which implies that R has the pattern which has a principal submatrix with q1=q1111≤2 and qk=qkkkk≤1 for k=2,3,4.Clearly,max{|q2323|,|q3434|}≤1.Set α=q2323,β=q3434.Then Hence α=β=0,and consequently,detB=?4,which contradicts B≥0. Claim(e)The case(l(π1),l(π2))=(4,4)does not occur. In this case,there exists k such that π1(k)=π2(k)whenever π1π2/=id,which breaks the condition(ii)(1)of Theorem 6.4.Therefore,this situation does not happen. In fact,the possible choices of π1and π2are from the following permutations: As π1/=π2and π1π2/=id,for any choice of π1,there are 4 possible choices of π2.For instance,letting π1=(2,3,4,1),the possible choices of π2are However,it is clear that,for any choice of π2above,there is some k such that π2(k)=π1(k),which breaks the condition(ii)(1)of Theorem 6.4. The proof of Theorem 6.5 is complete. □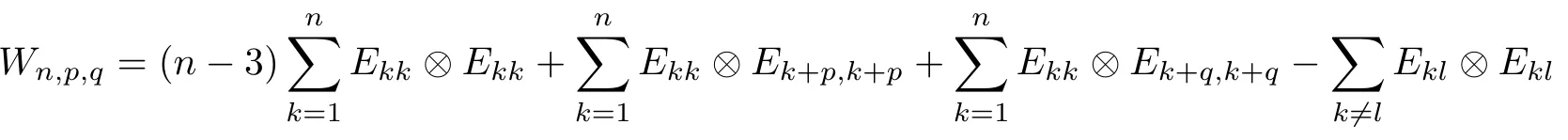
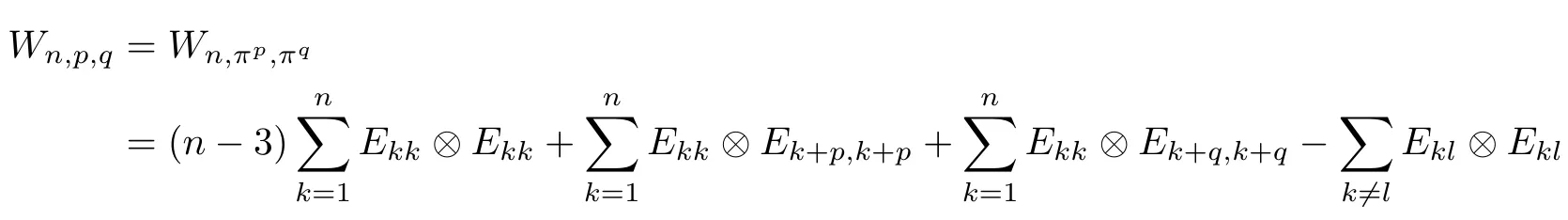


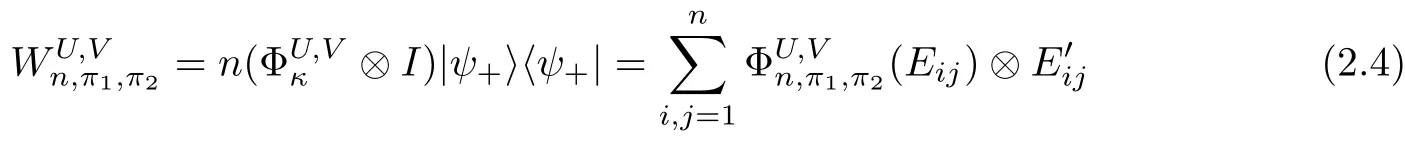


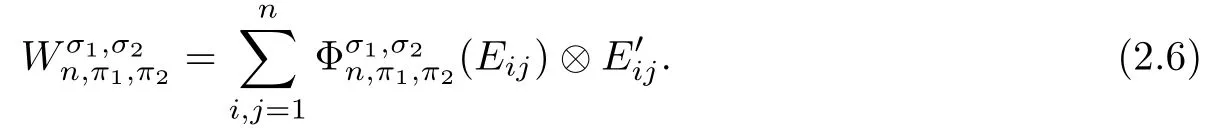
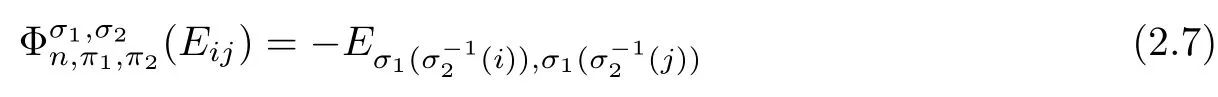
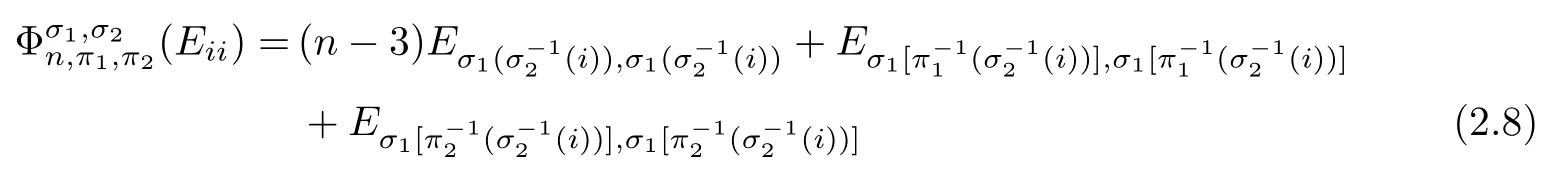

3 Comparing With EWs Constructed by Single Permutations


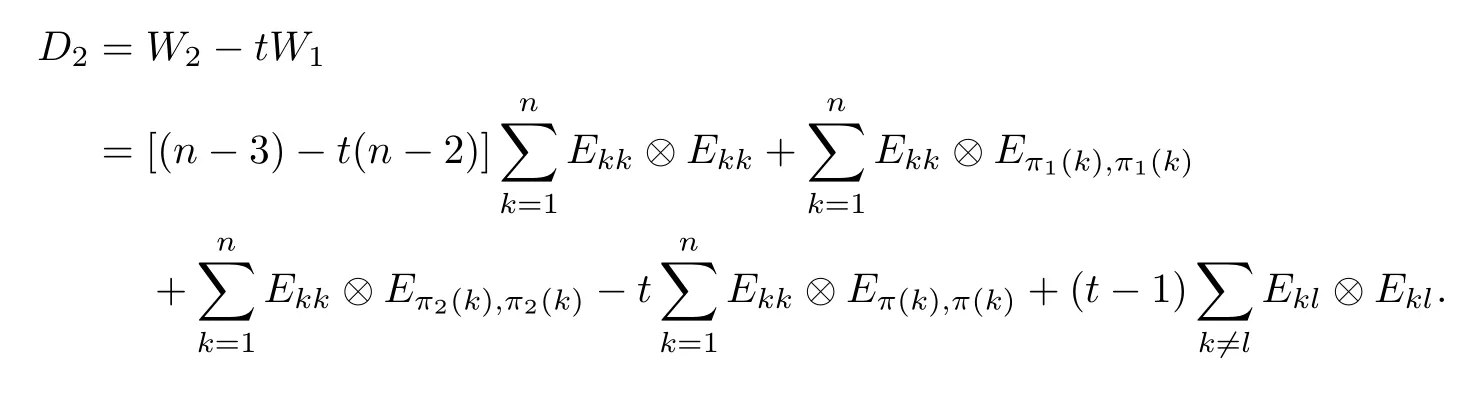



4 When is Wn,π1,π2 Decomposable?

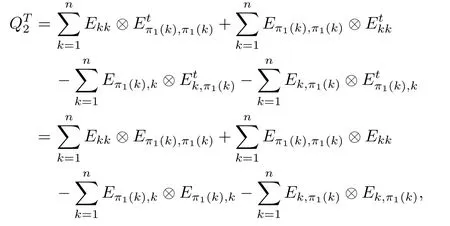
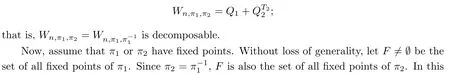
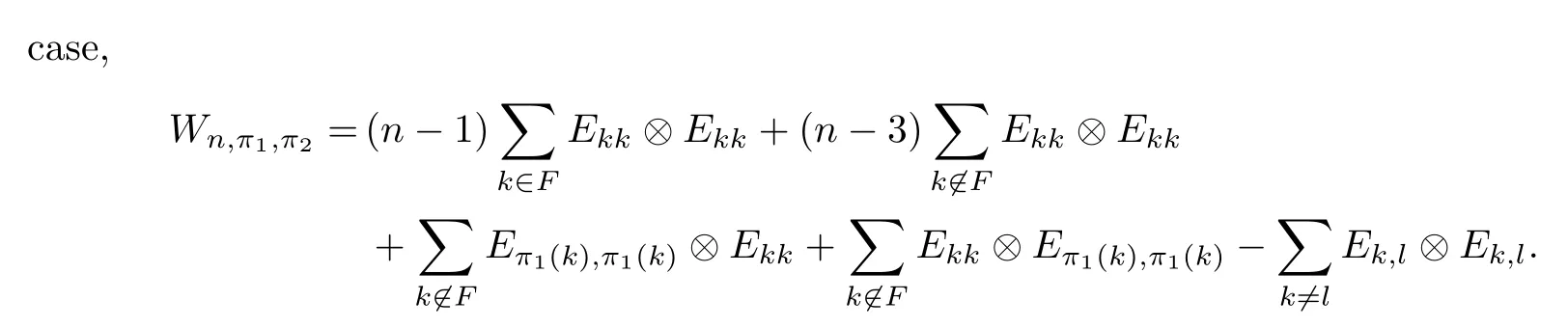


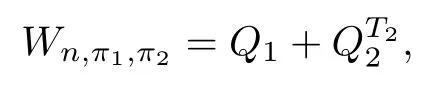

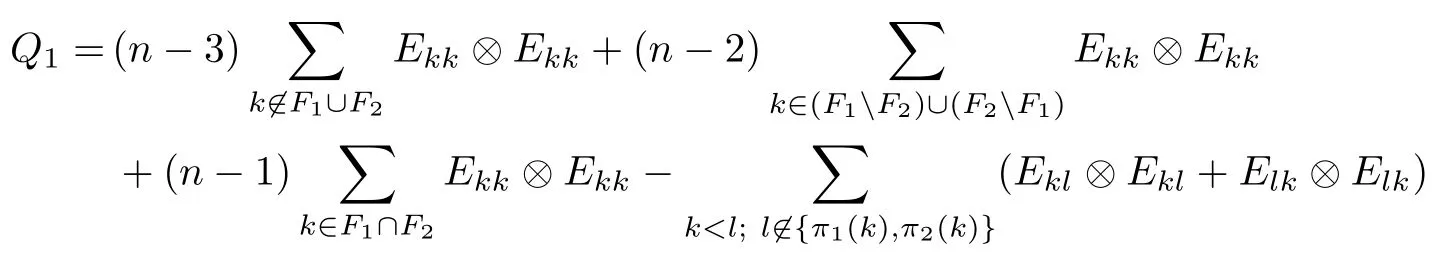

5 Application:Recognizing Entangled States

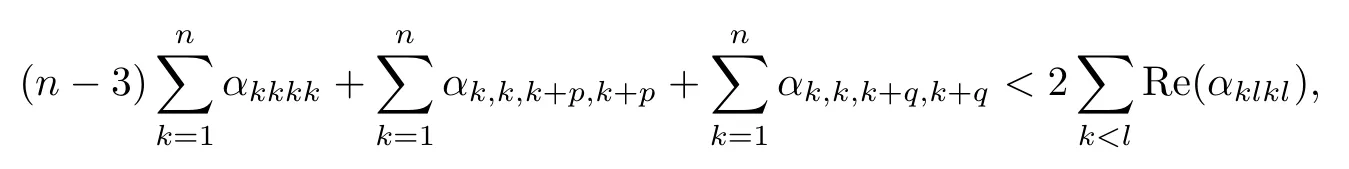

6 Low Dimension Cases
6.1 The case n=3




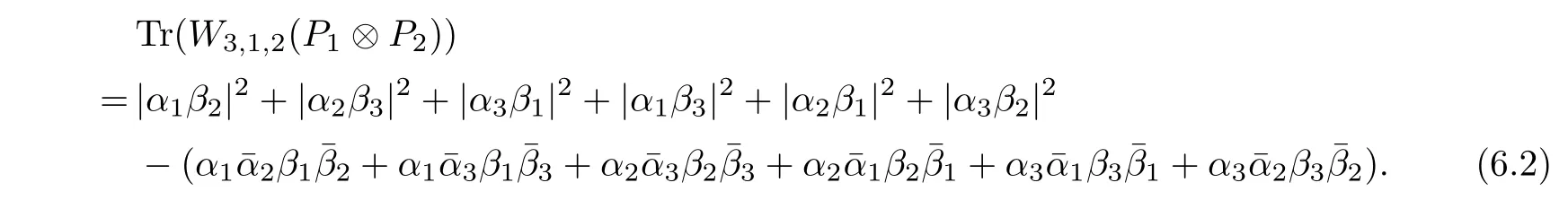
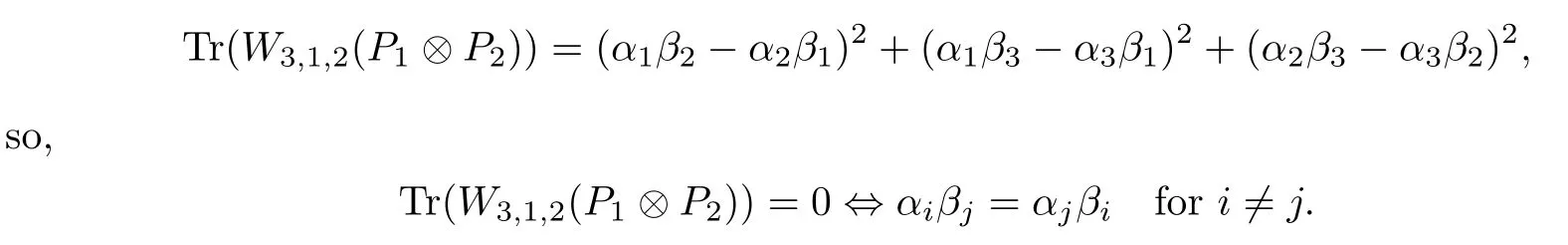

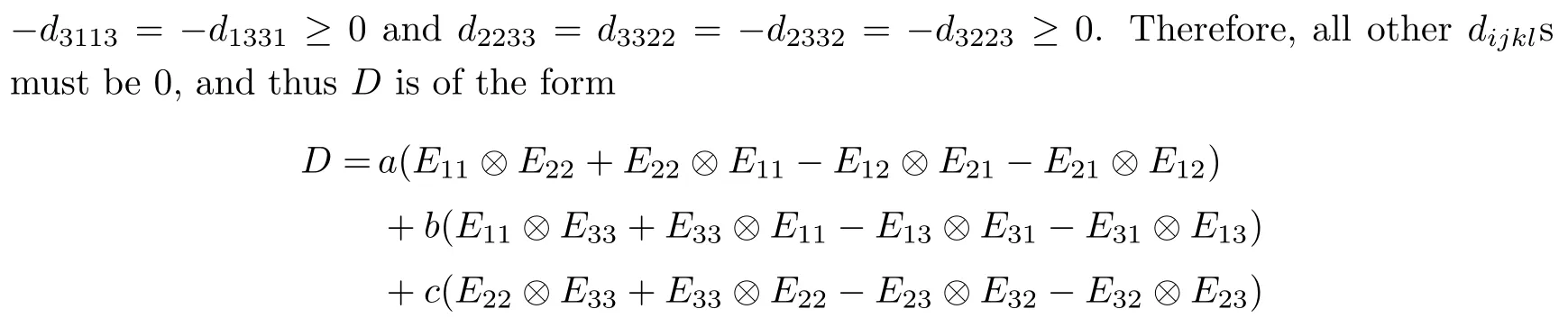
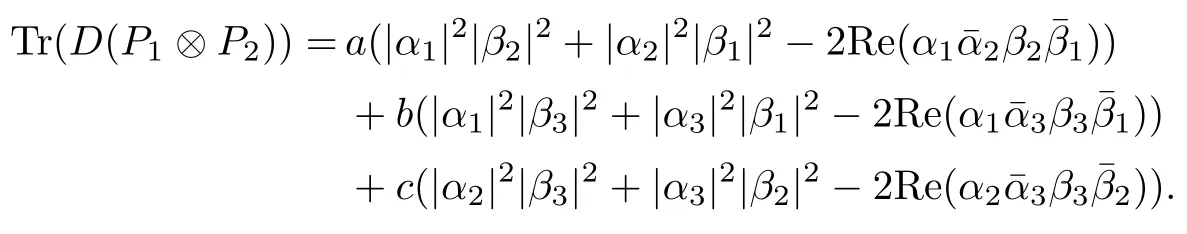
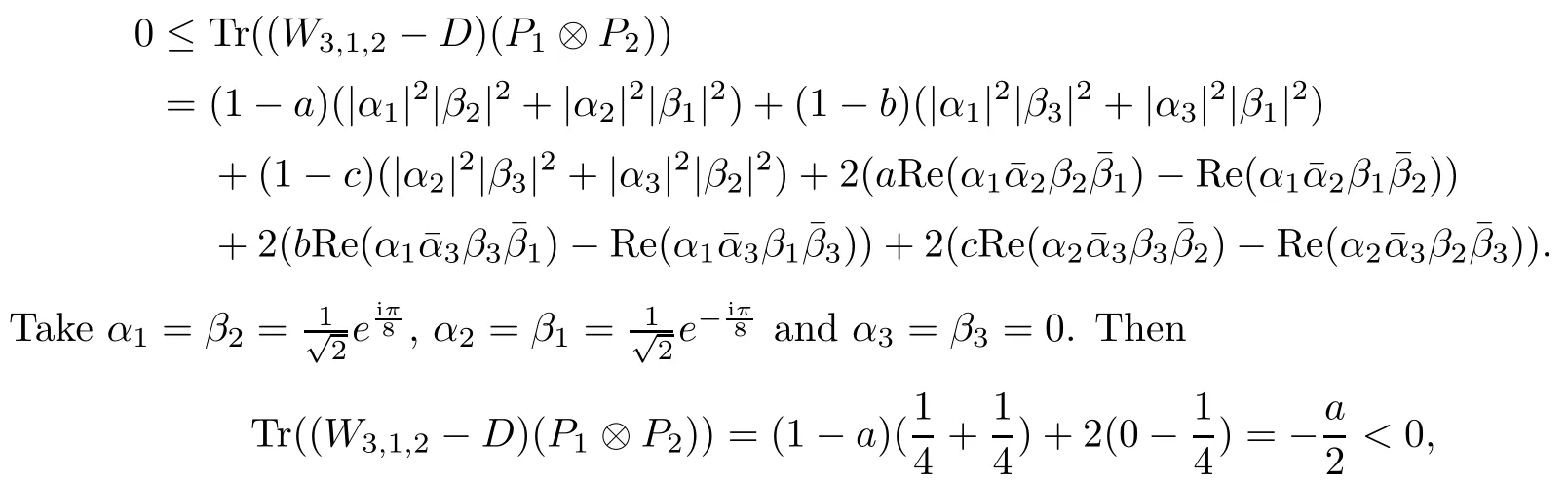
6.2 The case n=4
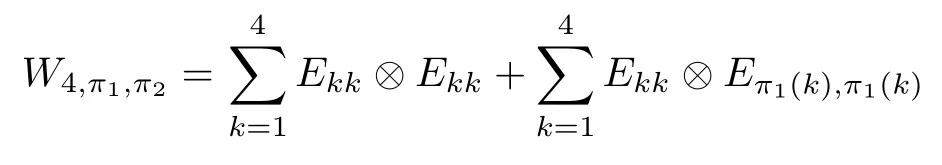
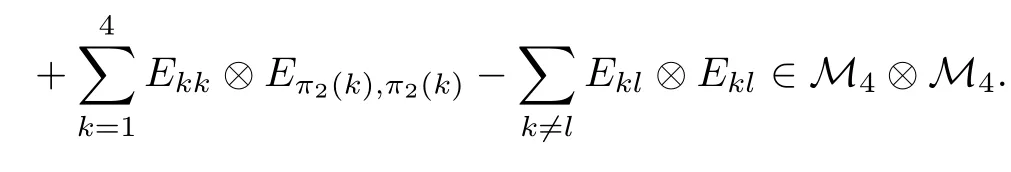



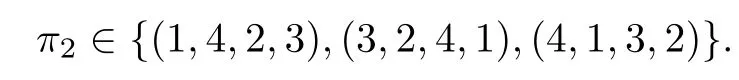
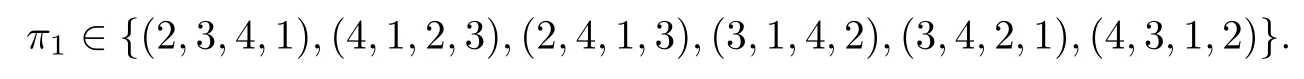
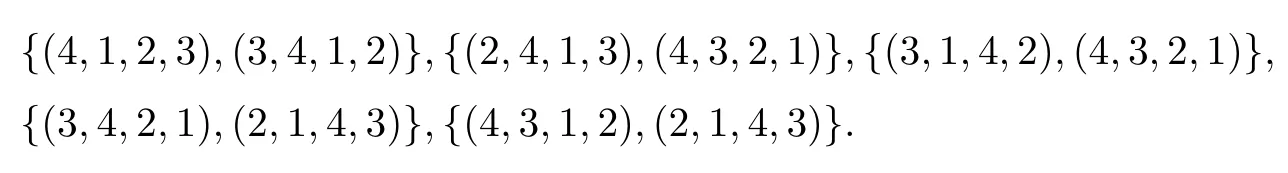
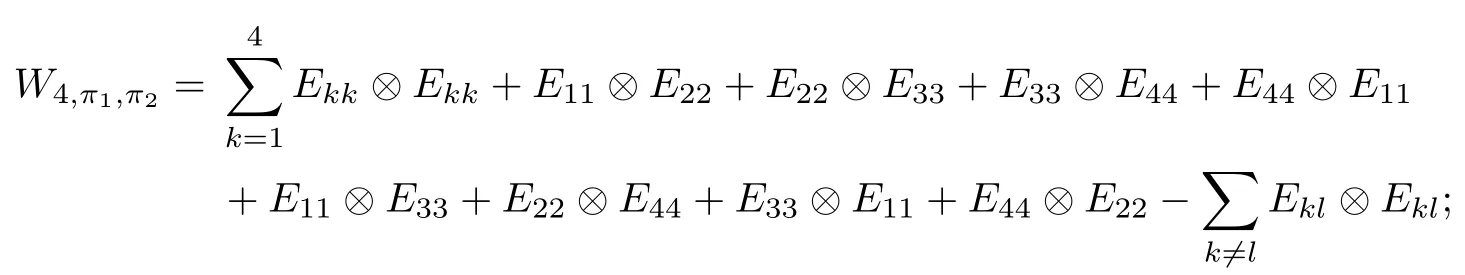


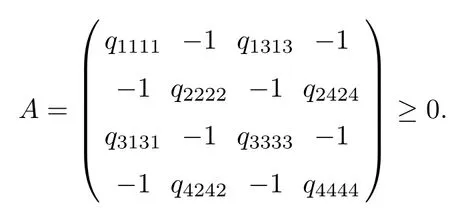










 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
