Instability of single-walled carbon nanotubes conveying Jeffrey fluid?
Bei-Nan Jia(賈北楠) and Yong-Jun Jian(菅永軍)
School of Mathematical Science,Inner Mongolia University,Hohhot 010021,China
Keywords: single-walled carbon nanotubes,Jeffrey fluid,relaxation time,retardation time
1. Introduction
Since the carbon nanotubes were discovered by Japanese researcher in 1991 years,[1]research on the microstructure of carbon nanotubes has become very challenging and potential topic in various science fields such as materials science,nanoscience and nanotechnology.[2–4]Carbon nanotubes have excellent electronic,mechanical,thermal,fluid transport,and gas storage properties.[5,6]Therefore,it is widely used in various fields,such as nano-mechanical systems,nano-biological devices,electrochemical devices,and fluid transmission.[7–12]In addition, the research on the carbon nanotubes filled with fluid is also becoming active. The key issue of exploring the carbon nanotubes conveying fluid is to obtain wall vibration property induced by flowing,which can promote structural instability. It has been known that the vibrating frequency of the single-walled carbon nanotubes(SWCNT)depends on the velocity of fluid. Yoon et al.[13,14]studied the effects of fluid velocity on free vibration and structural instability of SWCNT,and pointed out that internal moving could significantly affect the vibration frequency,especially for longer cantilevered carbon nanometers. Gogotsi et al.[15]analyzed multi-walled carbon nanotubes filled with fluid and studied the interaction between fluids and carbon walls. Euler–Bernoulli beam bending theory has been widely used to study the mechanical and structural properties of nanotubes. Lee and Chang[16]investigated the free lateral vibration of pipes as SWCNT filled with fluid. The effects of flowing velocity on the vibration frequency and mode shape of the SWCNT are analyzed using nonlocal elastic theory. Wang et al.[17]investigated the free vibration of embedded single-walled carbon nanotubes in multi-physics field. Ghavanloo et al.[18]analyzed the problem of the carbon nanotubes conveying fluid and resting on a linear viscoelastic Winkler foundation. Hosseini et al.[19]analyzed the vibration and stability of SWCNT conveying nanoflow embedded in biological soft tissues using modified nonlocal beam model. Moreover,many literatures concerning the natural frequency and damping frequency of CNTs conveying fluids were investigated.[20–22]
It should be noted that the fluids mentioned above are all non-viscous fluids. Khosravian and Rafii–Tabar[23]first investigated the instability of SWCNT filled with viscous fluid,and they observed that the viscosity of the fluid played an important role on instability of the SWCNT. Soltani et al.[24]studied the effects of fluid viscosity and the nonlocal parameter on the frequency of SWCNT based on nonlocal Euler–Bernoulli beam theory. In these papers, no works paid attention to the viscoelastic fluids. However, most of the fluids used in industry and biomedical treatment are viscoelastic fluids. In nanofluidic devices, Bandopadhyay and Chakraborty[25]and Jian et al.[26]studied streaming potential and electrokinetic energy conversion efficiency of viscoelastic fluids both in rigid nanochannel and in soft nanochannel (a rigid nanochannel whose surface is covered by charged polyelectrolyte layer).Recently,Hao and Jian[27]studied the effect of internally moving Maxwell fluid on instability of SWCNT. A new motion equation of a SWCNT conveying Maxwell fluid was derived,and the complex vibration frequencies of the SWCNT were obtained by DQM.They found viscoelastic parameter of fluid has important influence on the instability of the SWCNT.
Maxwell constitution equation is most simple description of viscoelastic fluids. In fact, apart from the relaxation time,retardation time of viscoelastic fluid may have crucial influence on instability of SWCNT. This article will extend non-Newtonian Maxwell fluid in Ref.[27]to Jeffrey fluid,and investigate the instability of the SWCNT filled with Jeffrey fluid.The effects of relaxation time and retardation time on the vibration frequency are discussed.It is expected to provide some theoretical basis in the research direction of SWCNT conveying fluid.
2. Formulation
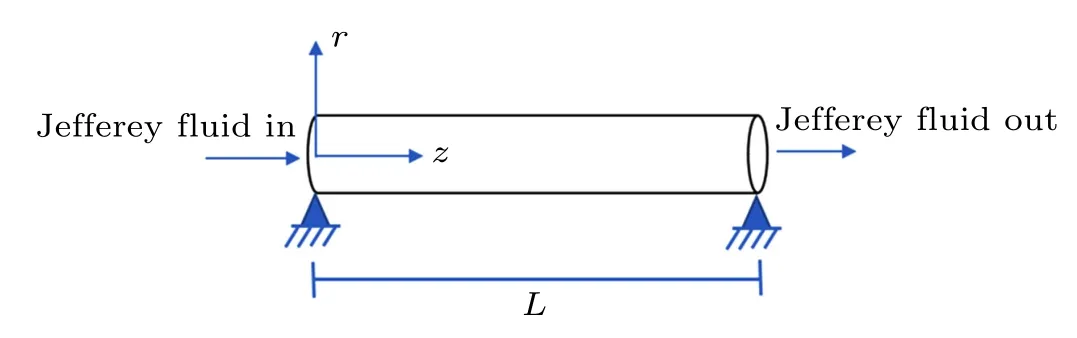
As shown in Fig.1, we consider a laminar, incompressible and Jeffrey fluid flowing through an SWCNT with two ends being fixed. The length of the SWCNT is L. A cylindrical coordinate system (r, θ, z) is established in the radial,circumferential and axial directions.For an SWCNT,its radial vibration equation is governed by the Euler–Bernoulli beam model[23]
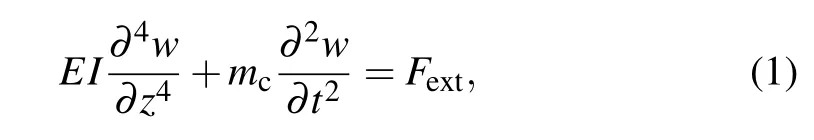
where w(z,t) and mcare the transverse displacement and the mass density of the beam per unit axial length of the SWCNT respectively, E and I are named as the Young’s modulus and the moment of inertia,Fextmeans external force acting in the transverse direction on the beam.
For fluid motion,the constitutive equation of Jeffrey fluid is written as
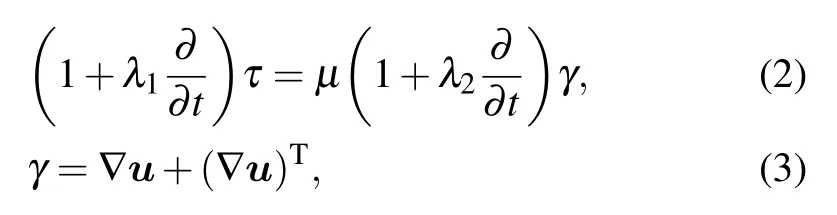
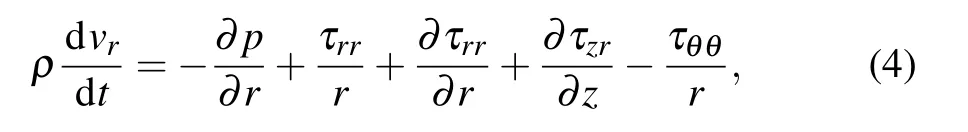
where p is pressure and ρ is the fluid density. Combining Eqs. (2) and (4) and eliminating shear stress yields the following Cauchy momentum equation of the Jeffrey fluid in the radial direction
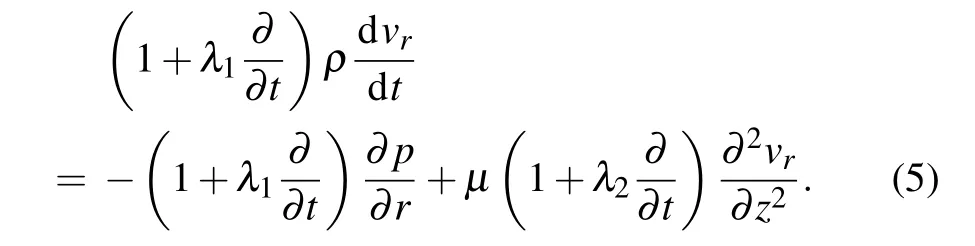
Taking the place of the external force Fextusing Af?p/?r,which represents the radical component of the pressure from the Jeffrey fluid, where Afis cross-sectional area per unit length of the fluid,using operator(1+λ1?/?t)to act Eq.(1),then substituting it into Eq.(5),we have
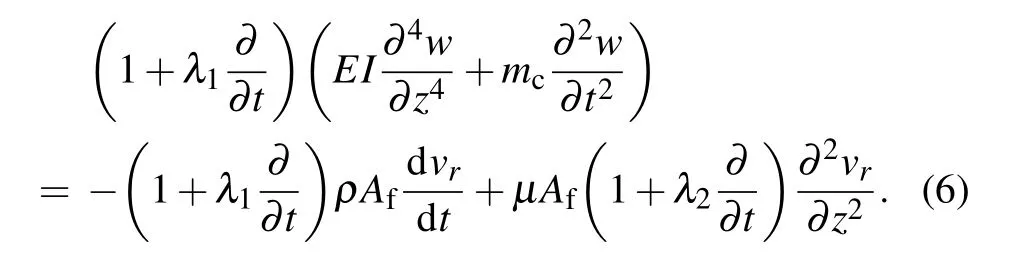
At the contact point between the fluid and the nanotube,their respective velocities and accelerations in the radical direction should be equal,[23]which gives
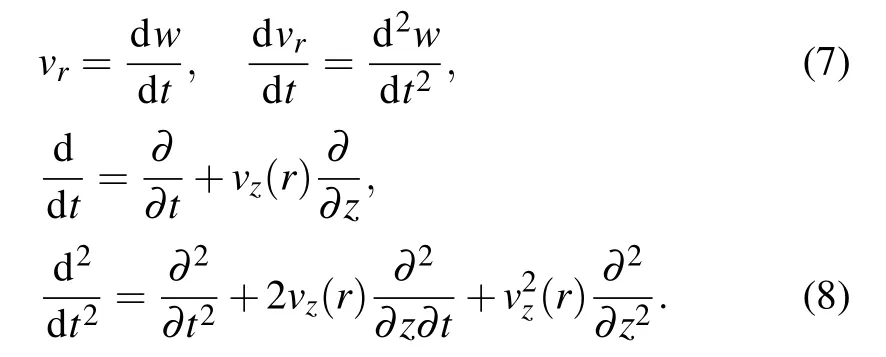
In order to circumvent non-slip condition (vz(r)=0) applies on the walls of the nanotube as a result of the viscoelasity of the fluid,a slip condition should be allowed at the moving wall and an averaged velocity is defined as follows:
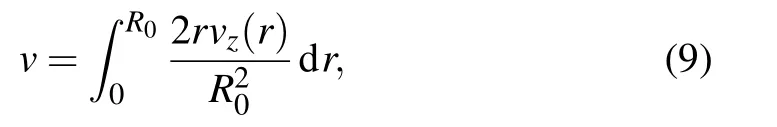
where R0is radius of the SWCNT.Leting mf=ρAf,substituting expression(8)into Eq.(6),we obtain
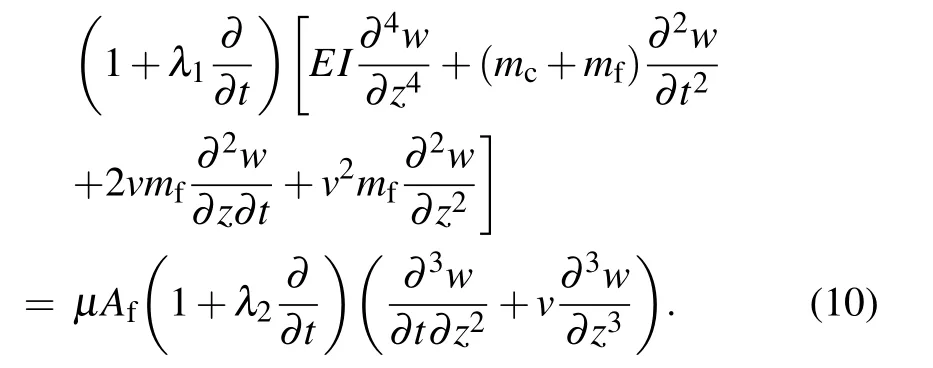
It is interesting to point out that if the retardation time effect is ignored, i.e., λ2=0, equation(10)reduces to equation(5)obtained by Hao and Jian.[27]Furthermore, if the relaxation time effect is neglected, i.e., λ1=0, equation (10) reduces to Eq. (11) in Ref. [23] when another part of external force and elastic medium effects are not considered. In addition,the clamped-clamped boundary conditions can be written as
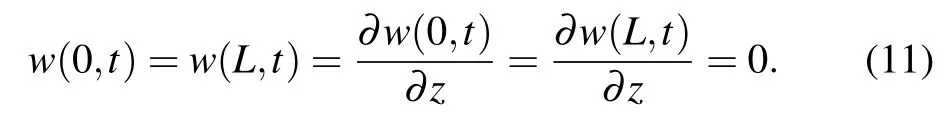
For more generality, introducing the following dimensionless quantities:
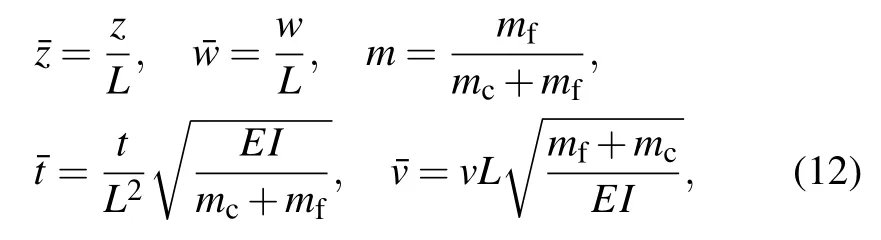
after dropping superscript of the horizontal line for convenience, equation (10) can be written as the following dimensionless form:
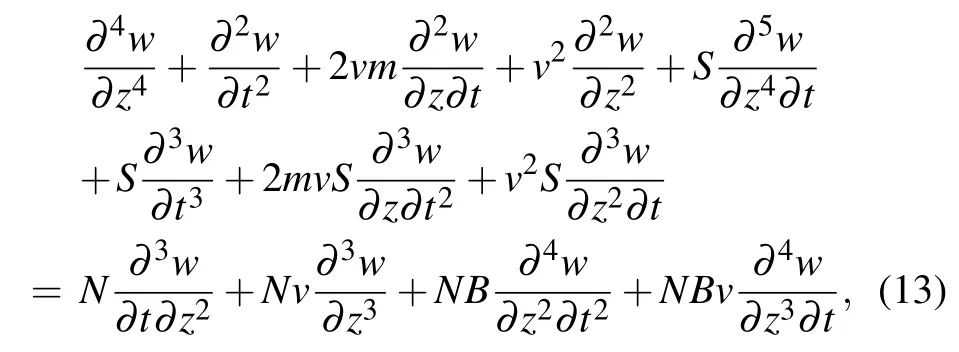
where the non-dimensional parameters in Eq.(13)are defined as
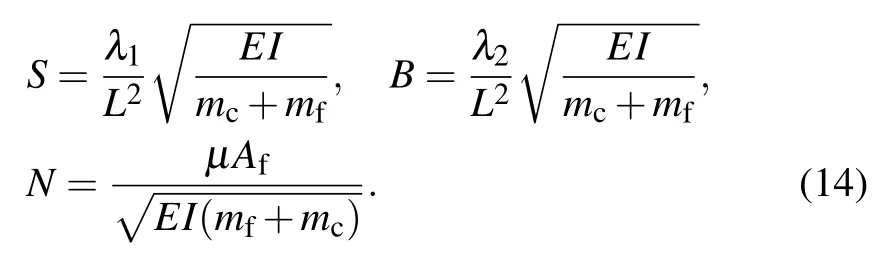
The physical meanings of S, B, and N are non-dimensional relaxation time, retardation time, and viscosity parameter,respectively. Accordingly, dimensionless boundary conditions(11)are
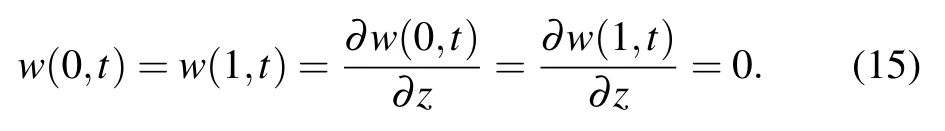
Letting w(z,t) = w(z)eiαt, where α is a complex vibration frequency,equation(13)becomes
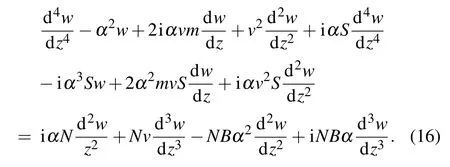
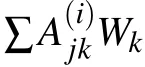
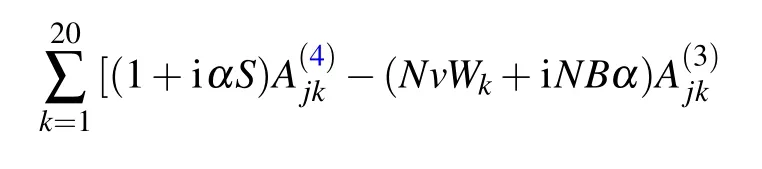
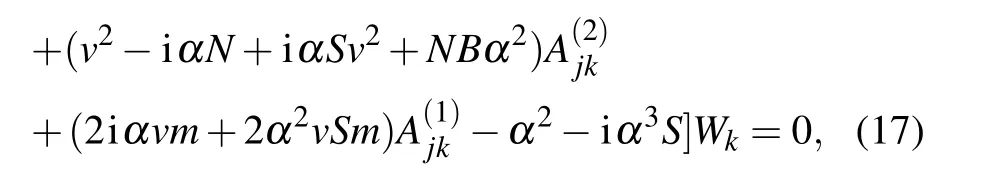
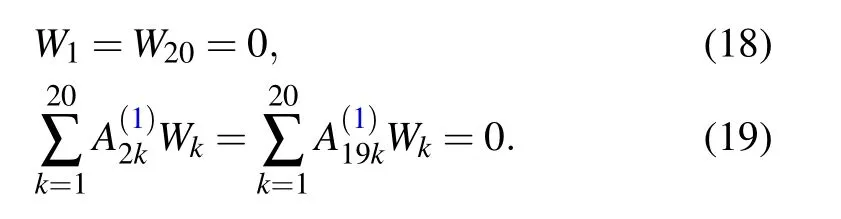
Then,putting the boundary conditions to first four rows.Thus,the final discrete form of Eq.(17)becomes[29,30]
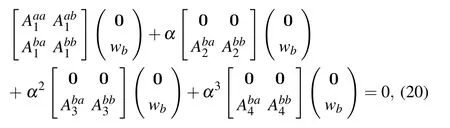
where the superscript a denotes elements associated with the boundary points while bmeans elements of internal points.Also, the column vector (0, wb)Tis generated by placing the boundary values to the first four lines. By using Eq.(20),we find
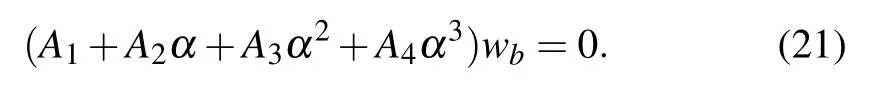
Based on Eq.(21),the generalized eigenvalue problem can be reformulated as

3. Results and discussion
In order to test the validity of our numerical method,figure 2 shows the natural frequency and decaying rate of the SWCNT for different dimensionless relaxation time S (0,0.0012, 0.00015, and 0.002) when dimensionless retardation time B=0 and dimensionless parameters N=0.01. When the dimensionless retardation time B=0,the model becomes the Maxwell fluid. Besides, when the dimensionless retardation time B=0 and relaxation time S=0,the model reduces to the Newtonian fluid. We observe that the result is the same as that obtained by Hao and Jian.[27]
Figure 3 illustrates the variations of the first three modes(the maximum absolute value of complex frequency α corresponds to mode 3) of natural frequency and decaying rate of the SWCNT with the dimensionless flow velocity v of Jeffrey fluid for different dimensionless retardation time B(0.001,0.005,and 0.008)when dimensionless relaxation time S=0.008. It is obvious from Fig.3(a)that the vibration frequency decreases and critical flow velocity increases as retardation time increases. That is to say, longer retardation time makes the SWCNT more stable. Moreover, when flow velocity v is greater than 8.68, mode 1 and mode 2 begin to combine, and the SWCNT undergoes a coupled mode flutter,which reflects the instability of SWCNT. When the flow velocity v is greater than 16.87,three modes are coupled,which shows the microtremor instability of SWCNT. It can be seen from Fig.3(b) that at the critical flow velocity value of 7.54,the appearance of conjugate complex numbers results in a nonzero decaying rate corresponding to combined unstable mode of mode 1 and mode 2. At this stage, the frequency of mode 3 is still stable. When the flow velocity is higher than 16.19,mode 3 also begins to become unstable.
4. Conclusion
We reported on the instability of an SWCNT conveying non-Newtonian Jeffrey fluid. It is an extension of the instability of an SWCNT conveying Maxwell fluid investigated in our previous study. Compared with Newtonian and Maxwell fluids, the constitutive relation of Jeffrey fluid is more complicated and the retardation time cannot be ignored. Based upon Euler–Bernoulli beam equation and Cauchy momentum equation, we first derived a new and more general vibration equation of an SWCNT conveying Jeffrey fluid. This equation can reduce to the results of Maxwell fluid[27]and Newtonian fluid.[23]In order to analyze the instability of an SWCNT conveying Jeffrey fluid, the DQM was utilized to yield the variations of the complex frequency with the flow velocity. We found interestingly that the vibration frequency decreases and the critical flow velocity increases with the retardation time.That is to say,longer retardation time makes the SWCNT more stable.
- Chinese Physics B的其它文章
- Quantum annealing for semi-supervised learning
- Taking tomographic measurements for photonic qubits 88 ns before they are created*
- First principles study of behavior of helium at Fe(110)–graphene interface?
- Relationship between manifold smoothness and adversarial vulnerability in deep learning with local errors?
- Weak-focused acoustic vortex generated by a focused ring array of planar transducers and its application in large-scale rotational object manipulation?
- Quantization of the band at the surface of charge density wave material 2H-TaSe2?

