蔣毓靈,劉力維

(南京理工大學理學院,江蘇 南京210094)

1.引言

近年來,從經(jīng)濟學的角度對各種排隊系統(tǒng)的策略行為進行研究已成為排隊理論研究的一個新趨勢.在經(jīng)濟學模型的排隊系統(tǒng)中,顧客進入排隊系統(tǒng)時,對于擁擠現(xiàn)象引起的等待,往往通過最大化自己的利益來決定自己的去留.但他們的行為往往會受到其他顧客的影響,也正是這種影響的存在,每個顧客的策略選擇都可看作是與其他顧客之間的博弈.從博弈論的角度對排隊系統(tǒng)中顧客行為的研究最早可追溯到1969年Naor[1]發(fā)表在《Econometrica》上的文章,他研究了簡單線性收支結構下的可見M/M/1排隊系統(tǒng).Edelson和Hildebrand[2]考慮了相同的排隊模型,但是是不可見情形,即到達的顧客在做出決策時無法獲得有關隊列狀態(tài)的任何信息.此后,大量學者開始了對Naor,Edelson和Hildebrand的排隊模型的擴展性研究,Economou和Kanta[3]討論了在可見情況下,具有故障和修復的M/M/1隊列的均衡策略.LI等人[4]研究了文[3]里的相同模型,但是是不可見情形.WANG和ZHANG[5]和YU等人[6]分別研究了在可見和不可見情況下,具有止步和延遲修復的M/M/1隊列的均衡策略.

在現(xiàn)實生活中,機器的啟動時間是不可忽略的.對于一些高能耗的服務,在人數(shù)很少時,我們不可能始終開著機器,否則從經(jīng)濟的角度來看,不利于利益的最大化,所以對關閉啟動的研究是很有必要的.許多文章都有對啟動時間的研究,部分可參考文[7-9].又由于昂貴的啟動成本,許多服務系統(tǒng)會采取一些控制策略來打開或關閉服務設施.在這些策略中,N策略是最經(jīng)常采用的.當系統(tǒng)變空時,服務臺將切換到休眠狀態(tài),直到系統(tǒng)中的顧客數(shù)量達到給定的閾值N時,服務臺才會被激活.帶有N策略的開創(chuàng)性工作可以追溯到Yadin和Naor[10]的多個假期的M/M/1排隊.GUO和Hassin[11]是第一個在具有N策略的單個馬爾可夫隊列中研究客戶和社會優(yōu)化的均衡進入策略的工作.另外,Burnetas和Economou[12],WANG等人[13]和ZHOU等人[14]也對N策略有所研究.

一些文章考慮了帶有N策略和服務臺故障的M/M/1排隊模型.本文最大的創(chuàng)新是增加了啟動狀態(tài),這使得模型和方程更加復雜.文章的其余部分安排如下:第2節(jié)是模型描述,第3節(jié)給出了服務臺不同狀態(tài)下的均衡到達率,第4節(jié)給出了均衡的社會收益函數(shù),第5節(jié)對均衡到達率和均衡社會收益進行了數(shù)值研究.

2.模型描述

我們考慮一個帶有N策略,啟動時間和服務臺故障的M/M/1排隊系統(tǒng).假設系統(tǒng)中顧客的到達服從參數(shù)為λ的泊松分布,服務規(guī)則是先到先服務(FCFS),服務時間服從參數(shù)為μ的指數(shù)分布.當服務臺處于休眠狀態(tài)時,它不為顧客提供任何服務,并且只有當系統(tǒng)中等待顧客人數(shù)達到給定的閾值N時,服務臺才會開始啟動,啟動時間服從指數(shù)分布,參數(shù)為θ.系統(tǒng)服務臺不是完全可靠的,在正常工作時有可能發(fā)生故障,假設顧客發(fā)現(xiàn)服務臺故障時就不再進入系統(tǒng),且服務臺發(fā)生的故障是完全故障,即服務臺停止服務并立即進行維修.服務臺發(fā)生故障的過程是參數(shù)為ξ的泊松過程,維修時間服從參數(shù)為η的指數(shù)分布.當服務臺處于正常工作狀態(tài)時,它遵循空竭服務規(guī)則.當系統(tǒng)變?yōu)榭諘r,服務臺關閉,即服務臺再次轉為休眠狀態(tài).另外我們假設顧客的到達過程,服務臺的服務過程,啟動過程,故障過程和維修過程均相互獨立.

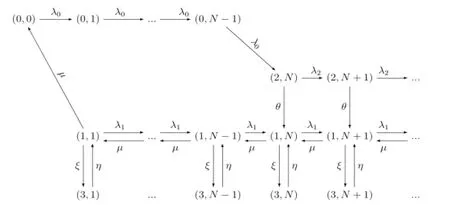
圖1 模型的狀態(tài)轉移圖

顧客在到達時需要決定是否進入系統(tǒng),一旦進入就不能離開,直到服務完成.假設每個服務完的顧客能得到R單位收益,每逗留單位時間需要支付C單位費用,逗留時間包括等待時間和服務時間.所有的顧客都是理性的,他們希望能使自己的凈收益最大化.更具體地說,當收益大于支出時,顧客進入系統(tǒng);收益小于支出時,顧客止步;收益等于支出時,進入和止步均可.

我們用{I(t),N(t),t ≥0}表示時刻t時系統(tǒng)的狀態(tài),其中I(t)表示服務臺的狀態(tài),N(t)表示系統(tǒng)中的顧客數(shù),

顯然,{I(t),N(t),t ≥0}是一個連續(xù)時間馬爾可夫鏈,狀態(tài)空間

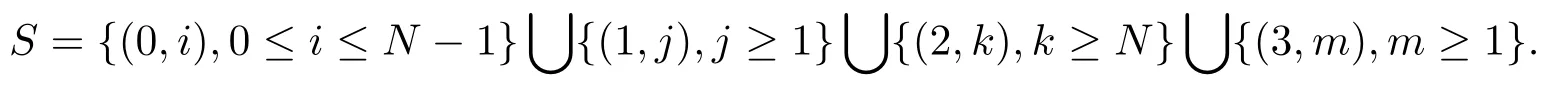
本文研究的是幾乎不可見情形,即到達的顧客只能知道服務臺的狀態(tài)而不能知道系統(tǒng)中顧客數(shù).實際上,顧客到達時的入隊概率和服務臺的狀態(tài)有關,我們假設所有顧客的入隊概率為qi(i=0,1,2,3),那么系統(tǒng)的有效到達率λi=λqi.又因假設顧客發(fā)現(xiàn)服務臺故障時就不再進入系統(tǒng),故q3=0,那么λ3=0.狀態(tài)轉移圖如圖1所示.

3.均衡到達率

在這一節(jié),我們研究均衡到達率.首先令{p(0,i),0≤i ≤N ?1;p(1,j),j ≥1;p(2,k),k ≥N;p(3,m),m ≥1}為馬爾可夫鏈{I(t),N(t),t ≥0}的穩(wěn)態(tài)分布,相應的部分生成函數(shù)如下:

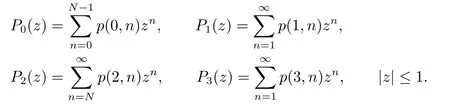
引理3.1在帶有N策略,啟動時間和服務臺故障的M/M/1排隊系統(tǒng)中,給定到達率(λ0,λ1,λ2),服務臺在狀態(tài)為0,1,2,3時的穩(wěn)態(tài)概率分別如下:

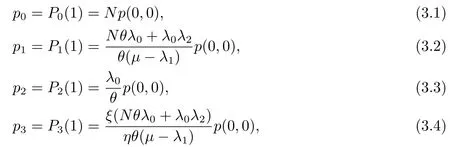
其中,

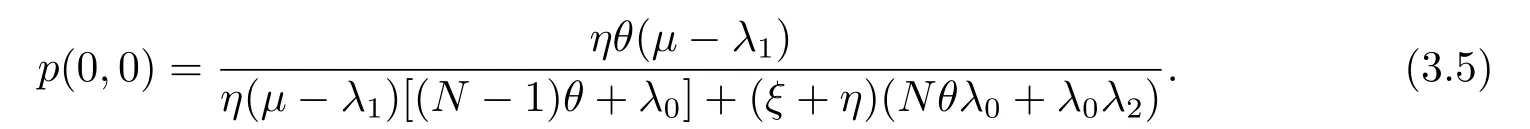
證穩(wěn)態(tài)分布的平衡方程如下:

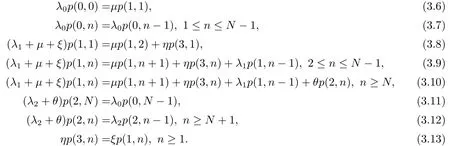
由(3.7)可得

在(3.8)-(3.13)兩邊同時乘以z的冪次,然后分別相加求和,可得到下列方程組,

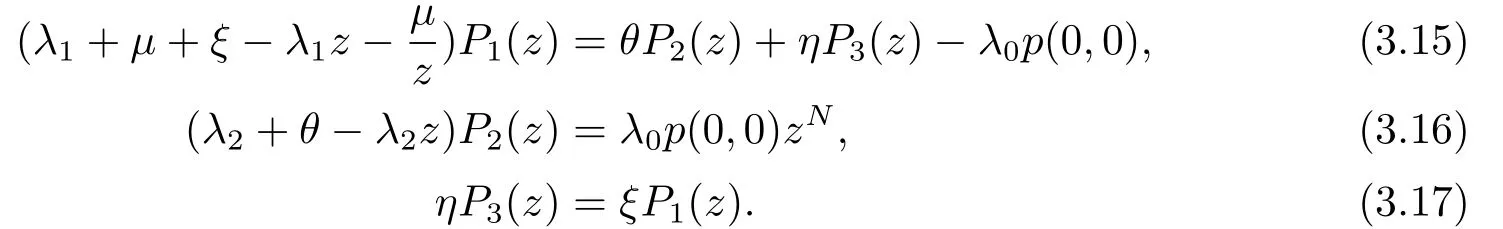
求解得

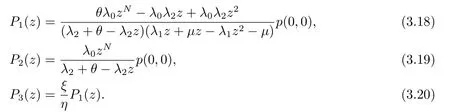
在(3.14),(3.18),(3.19),(3.20)中令z= 1,再由歸一化條件可解出p(0,0),然后我們就得到了P0(1),P1(1),P2(1),P3(1),如(3.1)-(3.4)所示.

我們分別定義T(0,j),0≤j ≤N ?1;T(1,j),j ≥1;T(2,j),j ≥N為標記顧客的平均逗留時間,該顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為0,1,2,且他在系統(tǒng)中第j個位置.

引理3.2在帶有N策略,啟動時間和服務臺故障的M/M/1排隊系統(tǒng)中,標記顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為0,1,2,且他在系統(tǒng)中第j個位置,那么他的平均逗留時間分別如下:

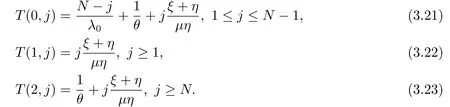
證首先,通過分析該排隊模型,我們可得到以下方程:

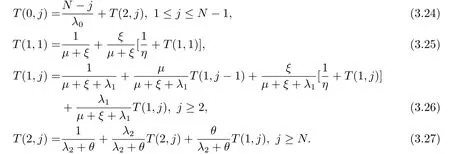
由(3,25)可得

由(3,27)可得

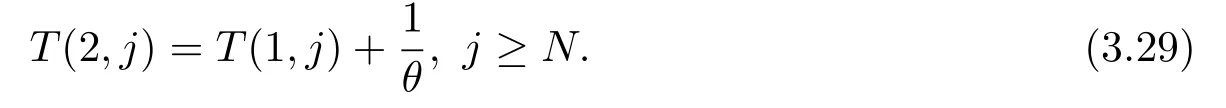
由(3.26)可得

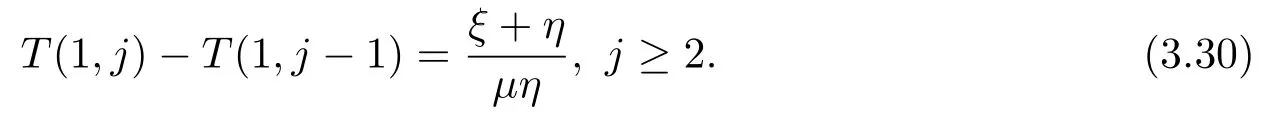
通過迭代(3.30),再結合(3.28)解出

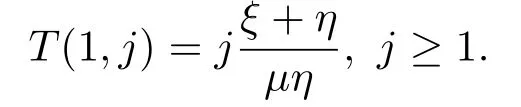
上式即(3.22).因此我們得到(3.21),(3.23).

定理3.1在帶有N策略,啟動時間和服務臺故障的M/M/1排隊系統(tǒng)中,給定到達率(λ0,λ1,λ2),當顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為0,1,2的平均逗留時間分別如下:

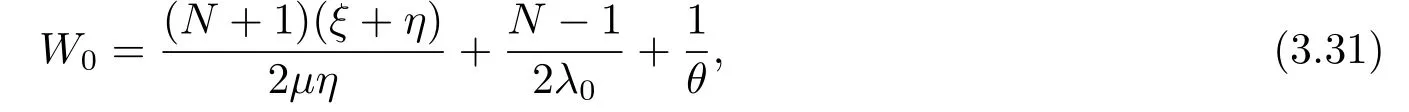
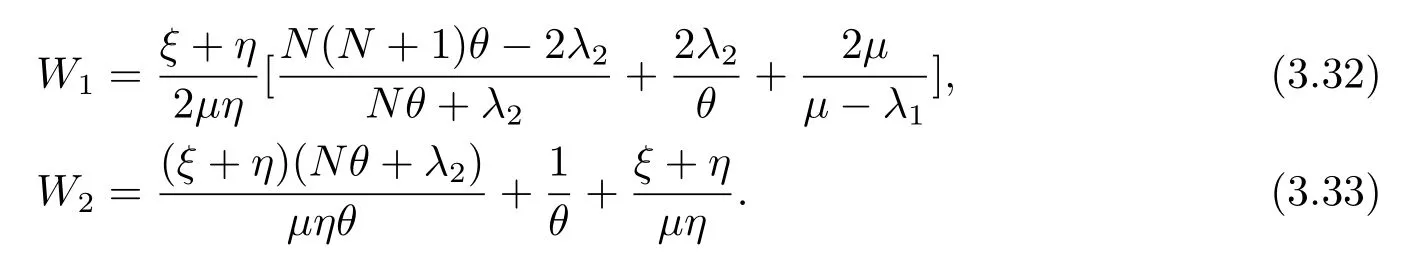
證定義W0(k)為一個到達顧客的平均逗留時間,該顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為0,系統(tǒng)中顧客數(shù)為k,那么他就是系統(tǒng)中第k+1個顧客,由引理3.2可得W0(k)=T(0,k+1)=同時定義p(k|0)為顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為0,系統(tǒng)中顧客數(shù)為k的概率,則那么當顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為0的平均逗留時間為

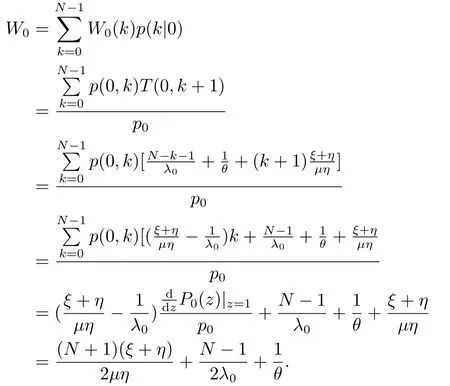
上式即(3.31).同理,當顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為1,系統(tǒng)中顧客數(shù)為k,相應的平均逗留時間和條件概率為

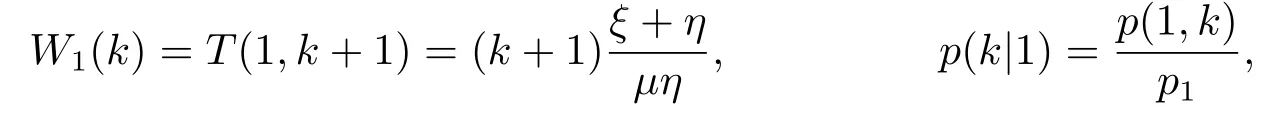
那么當顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為1的平均逗留時間為

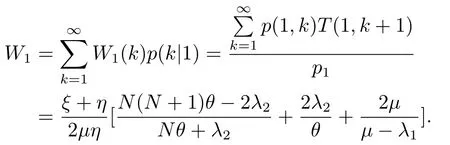
上式即(3.32).同理,當顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為2,系統(tǒng)中顧客數(shù)為k,相應的平均逗留時間和條件概率為

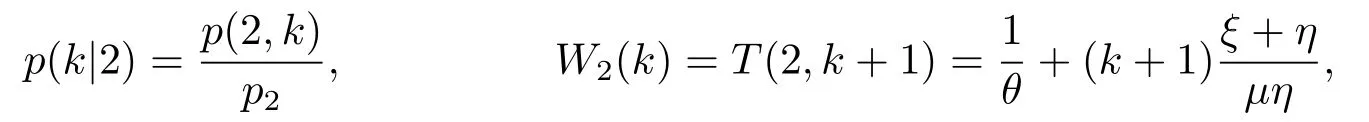
那么當顧客到達時發(fā)現(xiàn)服務臺狀態(tài)為2的平均逗留時間為

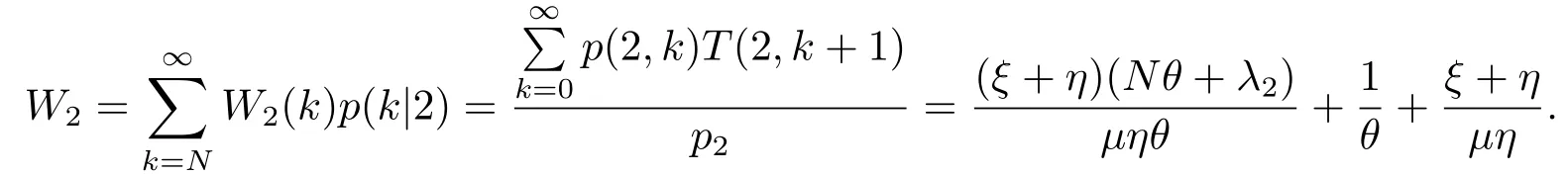
上式即(3.33).

顯然,從定理3.1中我們能發(fā)現(xiàn)平均逗留時間W0(W2)與到達率λ1和λ2(λ0和λ1)獨立,因此我們可以分別求相應的均衡到達率.另外,雖然W1只與λ0獨立,但是一旦給定λ2,W1關于λ1是單調遞增的,因此我們也能得到相應的均衡到達率.

令f(λ1,λ2)=W1.

定理3.2在帶有N策略,啟動時間和服務臺故障的M/M/1排隊系統(tǒng)中,當服務臺狀態(tài)為0時的均衡到達率

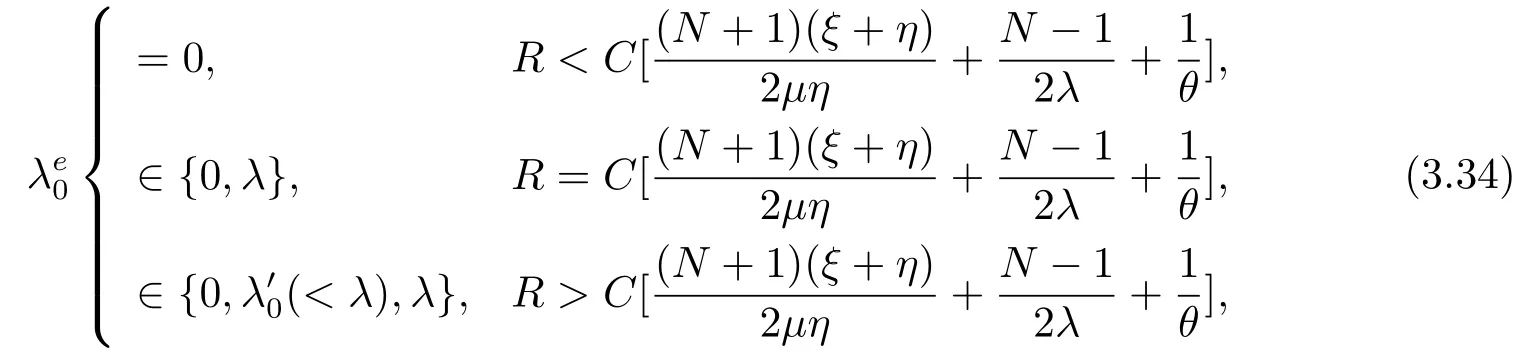
當服務臺狀態(tài)為2時的均衡到達率

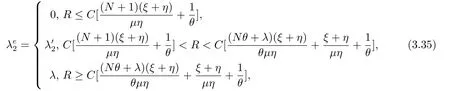
當服務臺狀態(tài)為1時的均衡到達率分三種情況,

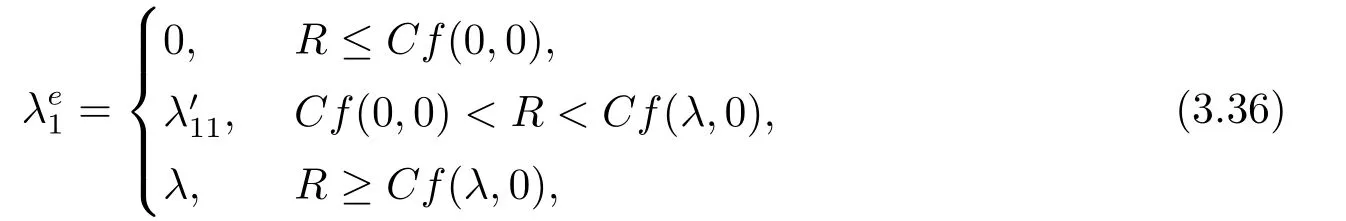
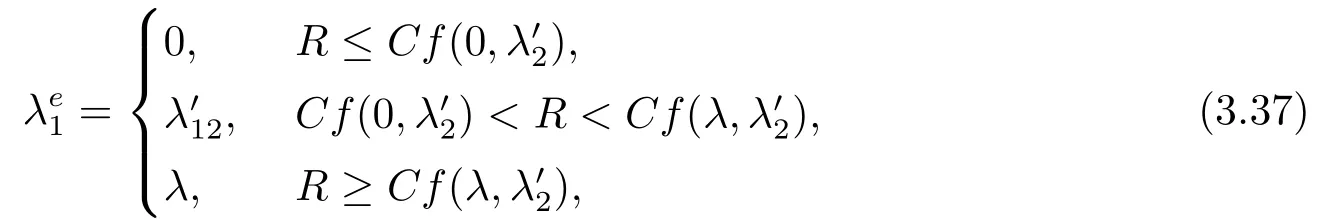
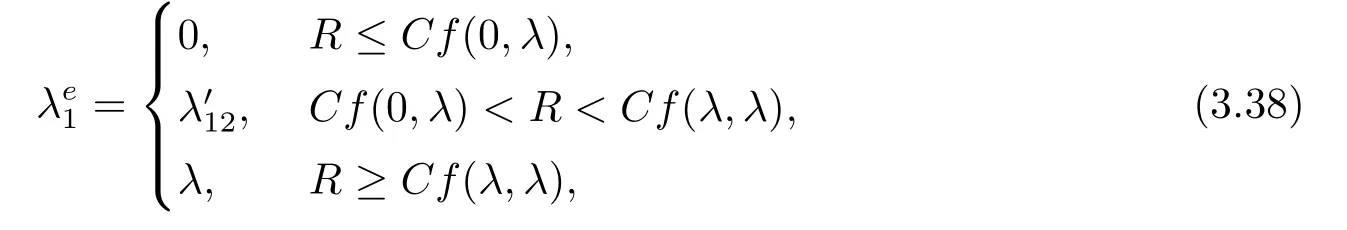
其中,

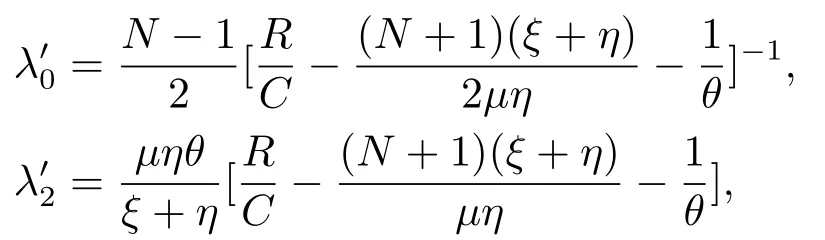
λ′11是R ?Cf(λ1,0)=0的根,λ′12是R ?Cf(λ1,λ′2)=0的根,λ′13是R ?Cf(λ1,λ)=0的根.

證首先,發(fā)現(xiàn)服務臺狀態(tài)為0時止步始終是顧客的均衡策略,因為如果沒有顧客決定進入系統(tǒng),那么系統(tǒng)就不會啟動,對于新來的標記顧客最優(yōu)的響應也是選擇止步,也就是說,λe0=0始終是顧客的均衡策略.

下面我們研究正的均衡到達率.根據(jù)收支結構,當顧客決定進入系統(tǒng)時,他的凈收益等于報酬R和逗留成本的差值,因此根據(jù)定理3.1,他的凈收益為

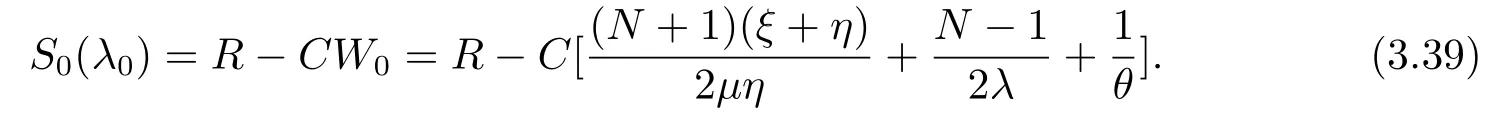
顯然,S0(λ0)關于λ0∈[0,λ]遞增,因此我們有以下結論:

同理,根據(jù)定理3.1,當服務臺狀態(tài)為2時,如果顧客決定進入系統(tǒng),他的凈收益為

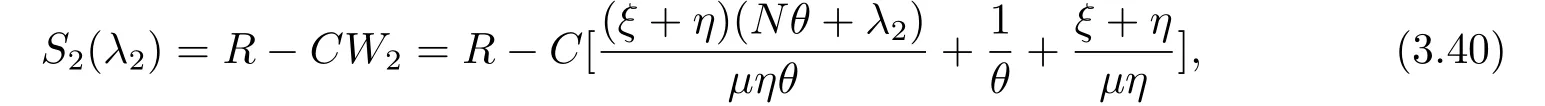
顯然,S2(λ2)關于λ2∈[0,λ]遞減,因此我們有以下結論:

同理,根據(jù)定理3.1,當服務臺狀態(tài)為1時,如果顧客決定進入系統(tǒng),他的凈收益為

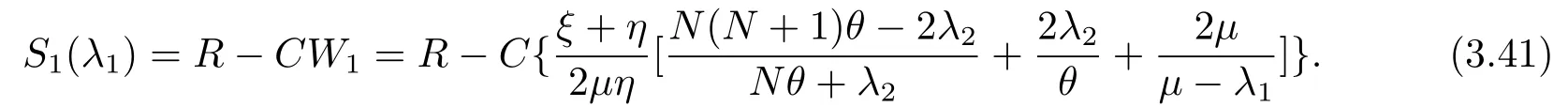
雖然W1只與λ0獨立,但是一旦給定λ2,W1關于λ1是遞增的,所以S1(λ1)關于λ1是遞減的.從而(3.36),(3.37),(3.38)的證明與(3.35)的證明是類似的.

4.均衡社會收益

在這一節(jié),我們給出了均衡社會收益函數(shù).

命題4.1均衡社會收益函數(shù)

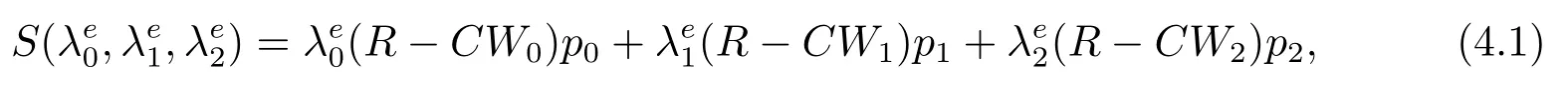
其中,

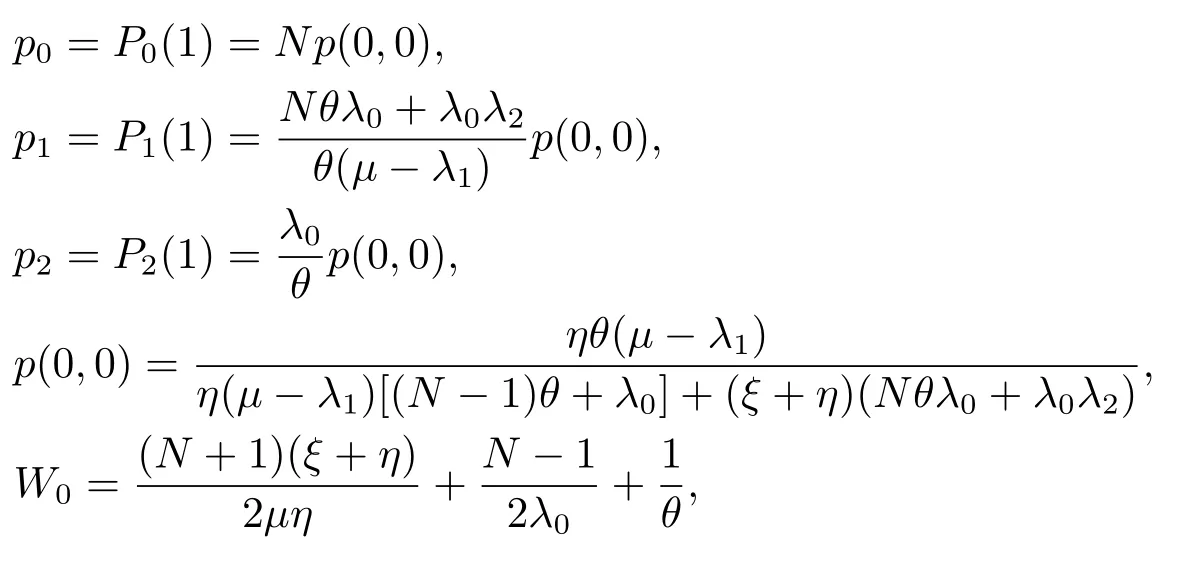
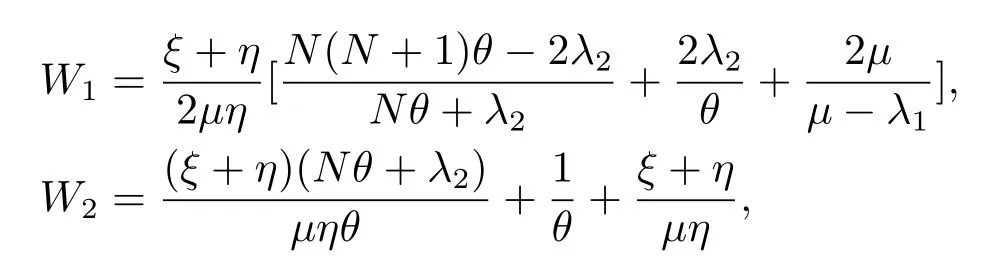
λ0,λ1,λ2分別由λe0,λe1,λe2代入,λe0,λe1,λe2在(3.34)-(3.38)中已給出.

5.數(shù)值分析

在這一節(jié),我們分別研究一些系統(tǒng)參數(shù)(N,R,θ,μ,ξ,η)對均衡到達率λe0,λe1,λe2和均衡社會收益S(λe0,λe1,λe2)的影響.

首先我們研究了閾值N對均衡到達率和均衡社會收益的影響,結果如圖2.根據(jù)圖2(a),我們能發(fā)現(xiàn)當N較小時(N ≤6),λe0=λe1=λe2=1,隨著N的增大,均衡到達率逐漸減小至零.這意味著當N較大時,顧客更傾向于止步.根據(jù)圖2(b),我們可以看出均衡社會收益關于N是遞減的.

圖2 均衡到達率λe0, λe1, λe2和均衡社會收益S(λe0,λe1,λe2)vs.N, 其中R=18, C =2,μ=ξ =η =2, λ=θ =1.

圖3研究的是報酬R對均衡到達率和均衡社會收益的影響.在圖3(a)中我們可以觀察到當R較小時(R ≤7),λe0=λe1=λe2=0,并且λe0,λe1,λe2隨著R的增大而增大.這意味著報酬R越大,顧客的凈利潤也會越大,他們就越傾向于進入系統(tǒng).在圖3(b)中也可以發(fā)現(xiàn)均衡社會收益隨著R的增大而增大.

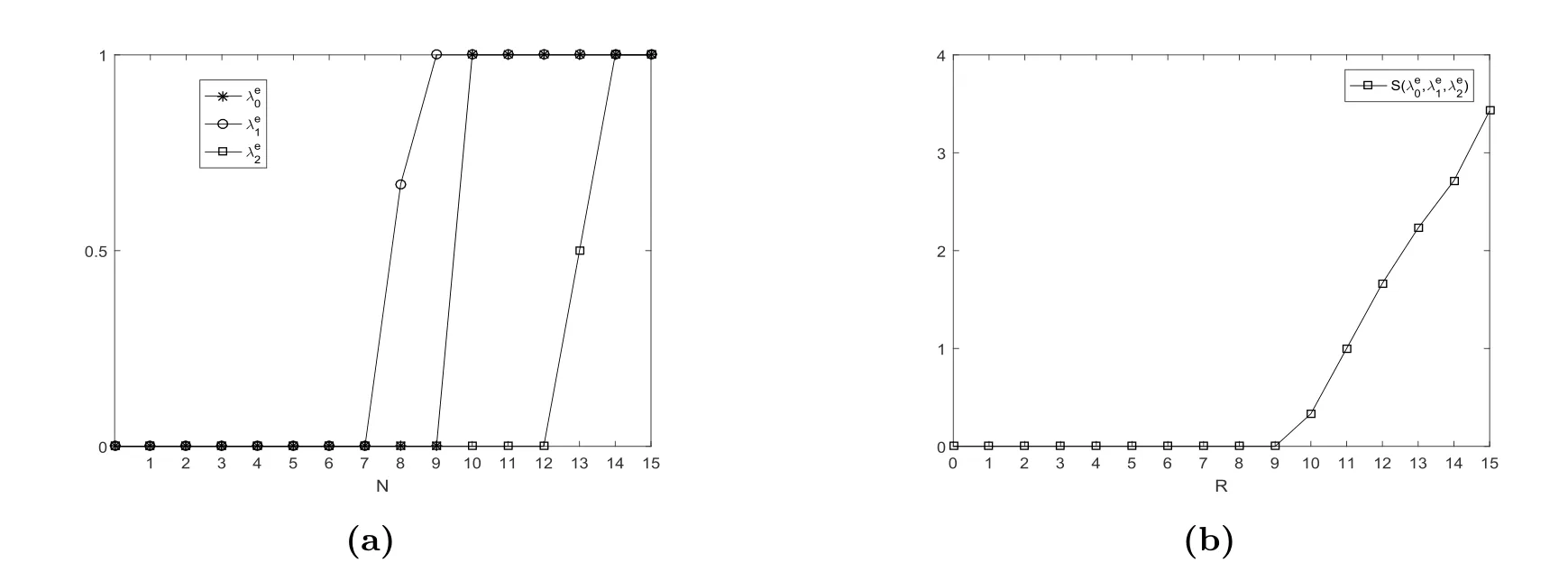
圖3 均衡到達率λe0, λe1, λe2和均衡社會收益S(λe0,λe1,λe2)vs.R,其中N =4, C =2,μ=ξ =η =2, λ=θ =1.

在圖4中,我們發(fā)現(xiàn)λe1=1,λe0和λe2關于參數(shù)θ遞增.當θ較大時,機器的啟動時間就較短,顧客的逗留時間隨之減少,顧客就愿意進入系統(tǒng).均衡社會收益關于參數(shù)θ也是遞增的.

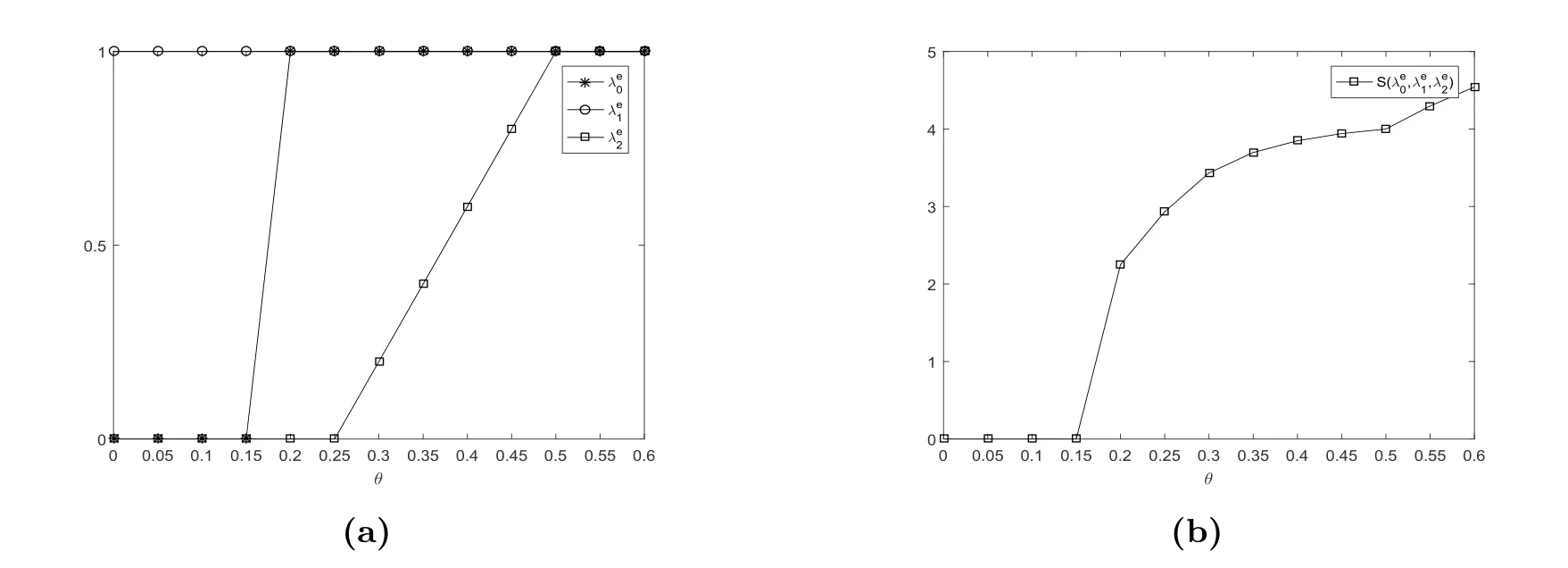
圖4 均衡到達率λe0, λe1, λe2和均衡社會收益S(λe0,λe1,λe2)vs.θ,其中N =4, R=18, C =2,μ=ξ =η =2, λ=1.

根據(jù)圖5,當μ >1時λe0= 1,λe1和λe2關于參數(shù)μ遞增.當μ較大時,顧客的服務時間減少,逗留成本也就減少,顧客也就更愿意進入系統(tǒng).顯然均衡社會收益關于參數(shù)μ也是遞增的.

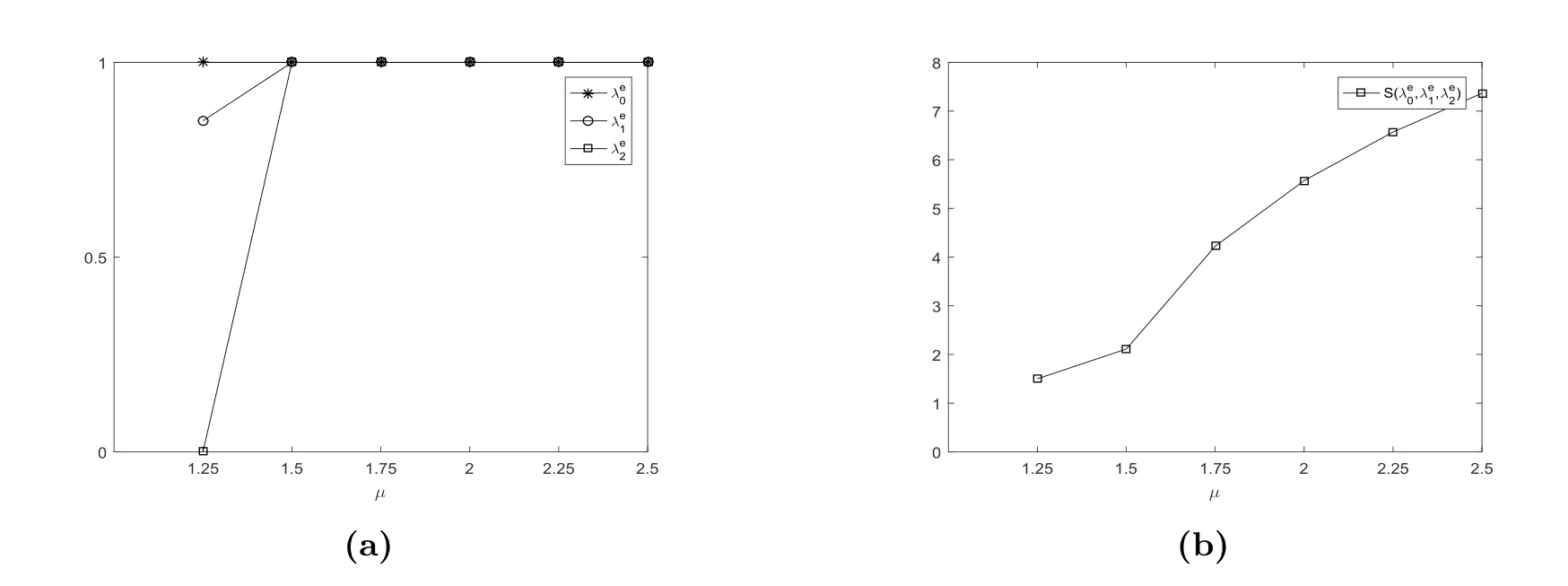
圖5 均衡到達率λe0, λe1, λe2和均衡社會收益S(λe0,λe1,λe2)vs.μ,其中N =4, R=18, C =2,ξ =η =2, λ=θ =1.

圖6研究了參數(shù)ξ對均衡到達率和均衡社會收益的影響.我們可以觀察到隨著ξ的增大,λe0,λe1,λe2逐漸減小至零.這意味著當ξ較大時,機器故障頻率變大,顧客更傾向于止步.均衡社會收益也是隨著ξ的增大逐漸減小至零.

圖6 均衡到達率λe0, λe1, λe2和均衡社會收益S(λe0,λe1,λe2)vs.θ,其中N =4, R=18, C =2,μ=η =2, λ=θ =1.

觀察圖7,我們可以發(fā)現(xiàn)λe0,λe1,λe2關于參數(shù)η遞增.均衡社會收益關于參數(shù)η也是遞增的.

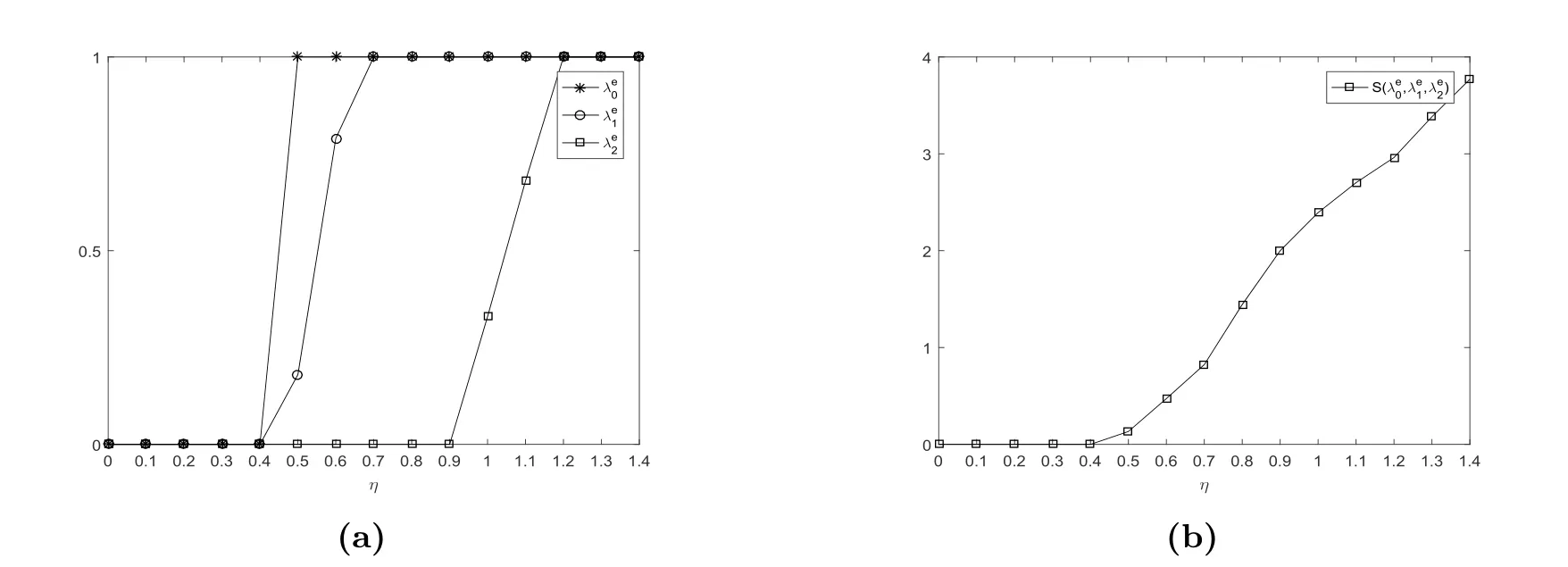
圖7 均衡到達率λe0, λe1, λe2和均衡社會收益S(λe0,λe1,λe2)vs.θ,其中N =4, R=18, C =2,μ=ξ =2, λ=θ =1.