INTERPOLATION OF LORENTZ MARTINGALE SPACES WITH VARIABLE EXPONENTS
ZHANG Xue-ying,ZHANG Chuan-zhou
(College of Science,Wuhan University of Science and Technology,Wuhan 430065,China)
Abstract:In this paper,we apply function parameters to real interpolation of Lorentz martingale spaces with variable exponents.Some new interpolation theorems concerning variable exponents Lorentz martingale spaces are formulated.The results that we obtain generalize some fundamental interpolation theorems in classical martingale Hptheory.
Keywords:Lorentz martingale spaces;variable exponents;function parameters
1 Introduction
The real interpolation spaceswere introduced in[1],and the theory of the spacesAθ,qhas been applied as a powerful tool to many branches of mathematics.These spaces are defined by using the function norm:
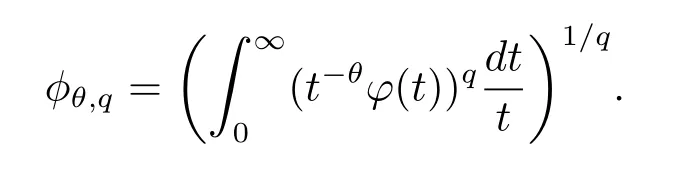
For the further applications of interpolation space theory,the idea of replacingAθ,qby a more general function norm to obtain more general interpolation spaces appeared.The initial work on such spaces was due to Kalugina[2].He used the function norm

to replaceφθ,q,wherefis a function parameter,which belongs to the function classBk.Later on,the theory of interpolation with a function parameter has been developed in an astounding way.For example see[3-7].
Interpolation of martingale Hardy spaces is one of the main topics in martingaleHptheory,and its theory has been successfully applied to Fourier analysis.In classical martingaleHptheory,it was proved by Weisz[8]and Long[9]that the interpolation spaces of martingale Hardy spaces were martingale Hardy-Lorentz spaces.Recently,Jiao[10,11]studied real interpolation of some weak martingale spaces,and Fan[12]considered real interpolation of some Lorentz martingale spaces.Ren and Guo[13]applied function parameters to consider the interpolation with a function parameter for Lorentz martingale spaces.Motivated by[13],the aim of this paper is to consider the interpolation with a function parameter for Lorentz martingale spaces with variable exponents.
2 Preliminaries



3 Some Lemmas



4 Main Results


- 數(shù)學(xué)雜志的其它文章
- RESEARCH ANNOUNCEMENT ON“LAGRANGE ELEMENTS HOLD DISCRETE COMPACTNESS BASED ON THE CLASSICAL VARIATIONAL FORMULATION OF THE MAXWELL EIGENPROBLEM”
- QUANTUM CODES FROM CYCLIC CODES OVER Fq+uFq+vFq
- LOWER BOUND FOR THE BLOW-UP TIME OF THE SOLUTION TO A QUASI-LINEAR PARABOLIC PROBLEM
- ABSTRACT CAUCHY-KOVALEVSKAYA THEOREM IN GEVREY SPACE:ENERGY METHOD
- |x|α(1≤α<2)在改進(jìn)的正切節(jié)點(diǎn)組的有理逼近
- 一類四階常微分方程周期邊值問題的正解

