段春暉, 譚 林,2, 戚文峰,2

1. 中國人民解放軍戰(zhàn)略支援部隊信息工程大學(xué), 鄭州450001

2. 數(shù)學(xué)工程與先進計算國家重點實驗室, 鄭州450001

1 引言

隨著移動通信和物聯(lián)網(wǎng)的發(fā)展, 射頻識別系統(tǒng)(RFID) 和智能卡等設(shè)備的加密被廣泛應(yīng)用, 海量信息加密和有限資源處理間的矛盾日益突顯, 傳統(tǒng)的加密算法無法適用于資源受限的環(huán)境, 密碼算法的輕量化越來越受到關(guān)注. PRESENT[1], SIMON 和SPECK 等[2]輕量級密碼算法先后被提出, 它們使用小規(guī)模的密碼組件, 在硬件實現(xiàn)方面有著明顯的優(yōu)勢. PRINCE[3]密碼算法是J. Borghoff 等在2012 年的亞密會上提出的一個輕量級分組密碼, 它基于FX 結(jié)構(gòu)[4]設(shè)計, 具有α-反射性質(zhì), 解密過程可以通過稍微改變密鑰進行加密來實現(xiàn). 這種特性使PRINCE 在硬件實現(xiàn)上具有優(yōu)勢, 但也使得其安全性受到擔憂, H.Soleimany 等[5]針對某些特定的α 值在相關(guān)密鑰模式下可以攻擊全輪的PRINCE 變種, 但這里不包括PRINCE 算法的α 值.

學(xué)者們對PRINCE 算法的安全性進行了大量分析, 表1 羅列了目前在單密鑰模式下對PRINCE 算法不同輪數(shù)版本的主要分析結(jié)果. J. Jean 等給出了4 輪和6 輪PRINCE 的積分攻擊[6]. 王小云團隊使用中間相遇攻擊方法攻擊了8 輪和9 輪PRINCE[7]. 雖然PRINCE 的輪密鑰除了首尾白化外都相同, 但仍假設(shè)差分特征概率等于各輪差分概率的乘積, A. Canteaut 等[8]構(gòu)造了5 輪和6 輪的多重差分區(qū)分器, 攻擊了9 輪和10 輪PRINCE; 趙光耀等[9]給出了5 輪和6 輪的截斷差分區(qū)分器, 并攻擊了7 輪PRINCEcore. P. Derbez 等[10]將中間相遇方法和SAT 方法相結(jié)合, 攻擊了10 輪PRINCE. P.Morawiecki 利用積分和高階差分分析, 給出了4 輪至7 輪PRINCE 實際的攻擊[11]. 隨后, R. Posteuca等改進了6 輪PRINCE 的積分攻擊, 降低了數(shù)據(jù)量和計算量[12]. 利用預(yù)存儲技術(shù), S. Rasoolzadeh 等改進了4 至6 輪的積分攻擊和7 輪的高階差分攻擊[13]. L. Grassi 等利用子空間路徑給出了只需要8 個選擇明文的4 輪PRINCE 的截斷差分攻擊[14].

本文將文獻[8] 的多重差分技術(shù)稍作改變, 考慮輸入差分為固定值, 輸出差分為選定的集合, 給出了目前輪數(shù)最長的7 輪PRINCE 區(qū)分器, 并對8 輪PRINCE 進行了密鑰恢復(fù)攻擊. 本文給出的7 輪差分區(qū)分器的概率為2?56.89, 8 輪PRINCE 的密鑰恢復(fù)攻擊所需的數(shù)據(jù)復(fù)雜度為261.89個選擇明文, 時間復(fù)雜度為219.68次8 輪加密, 存儲復(fù)雜度為215.21個16 比特計數(shù)器. 相比目前已知的8 輪PRINCE 密鑰恢復(fù)攻擊的結(jié)果, 包括將A. Canteaut 等的10 輪攻擊方案減到8 輪, 本文的時間復(fù)雜度和D×T 復(fù)雜度都是最低的.

2 PRINCE 密碼算法簡介

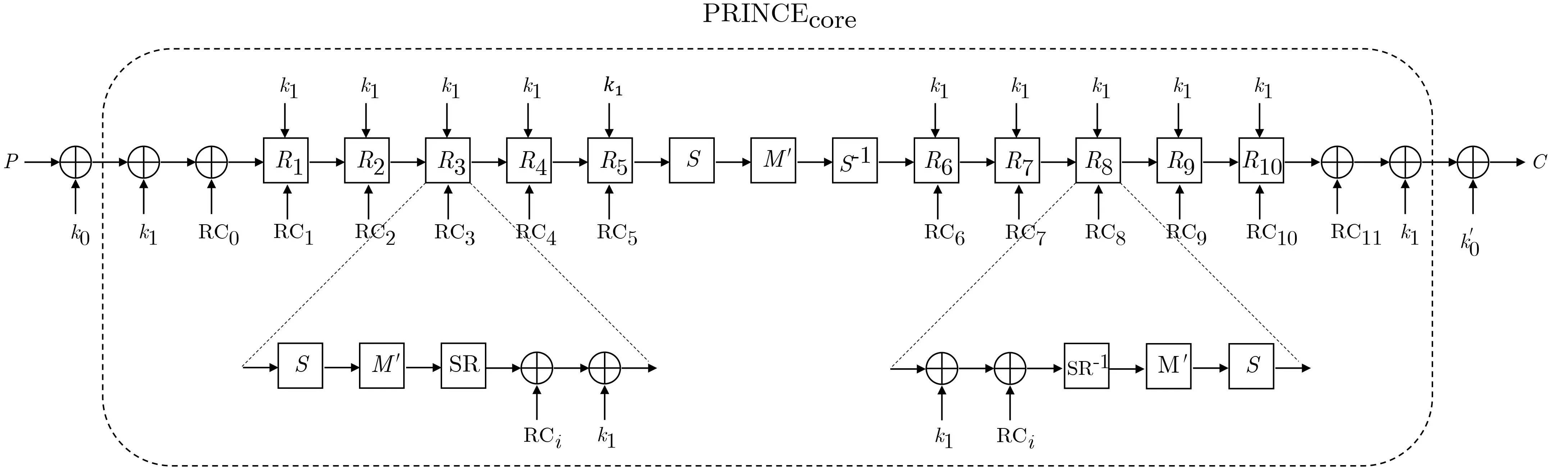
圖1 PRINCE 算法結(jié)構(gòu)圖Figure 1 Structure of PRINCE

將PRINCE 的64 比特狀態(tài)X 看成一個4×4 的矩陣, 每一個塊單元為4 比特, 本文中我們記X(l)為表示X 的第l 塊, l ∈{0,1,··· ,15}, 塊的順序如圖2 所示. 算法的輪函數(shù)可表示為R = AK ?ARC ?SR ?M′?S, 包括以下5 個變換:

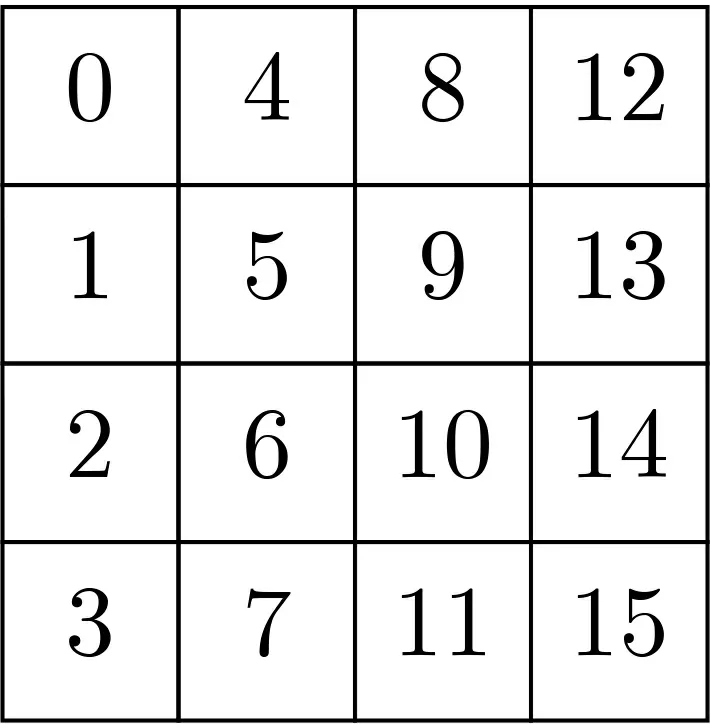
圖2 狀態(tài)X 的16 個塊標記Figure 2 State X

S 層: 16 個塊同時查詢一個4 比特的S 盒, S 盒如表2 所示.

表2 PRINCE 的S 盒Table 2 S-box of PRINCE

擴散層M′: 擴散層對應(yīng)對角矩陣M′=diag( ?M0, ?M1, ?M1, ?M0), 作用在狀態(tài)X 上為

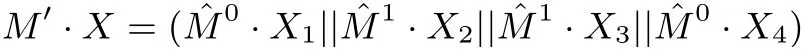
這里Xi表示X 的第i 列, 1 ≤i ≤4, 矩陣 ?M0, ?M1分別為:

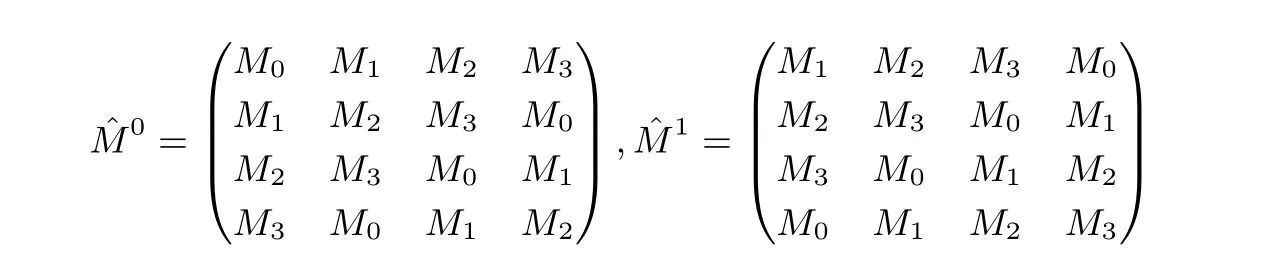
其中

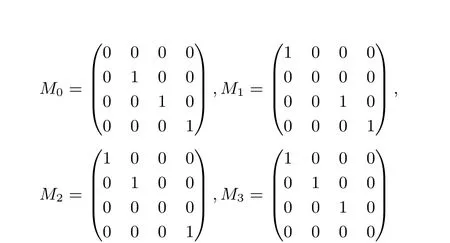
行移位SR: 與AES 的行移位操作相同, 將狀態(tài)的第i 行向左循環(huán)移動i 個塊, 0 ≤i ≤3.

輪常數(shù)加ARC: 比特異或一個64 比特輪常數(shù)RCi,0 ≤i ≤11.

密鑰加AK: 比特異或64 比特密鑰k1.

3 準備工作

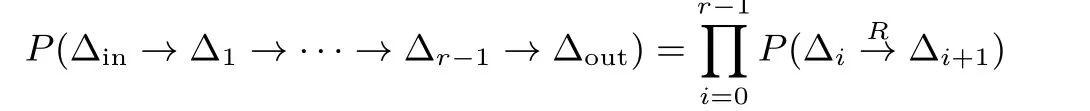
設(shè)?in和?out分別表示r 輪的輸入差分和輸出差分, 則r 輪差分概率

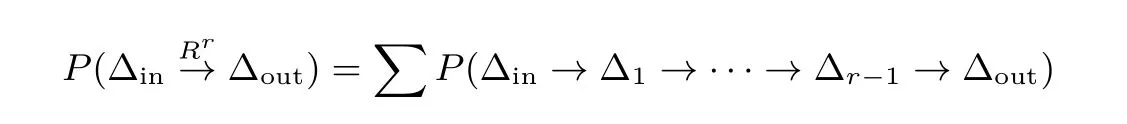
圖3 差分模式?i,i=1,2,··· ,8Figure 3 Difference pattern ?i,i=1,2,··· ,8

文獻[9] 指出了矩陣 ?M0和 ?M1具有如下性質(zhì): 如果δ ∈{1,4,5}, 則

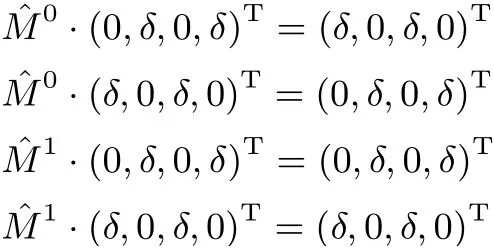
如果δ ∈{2,8,10},

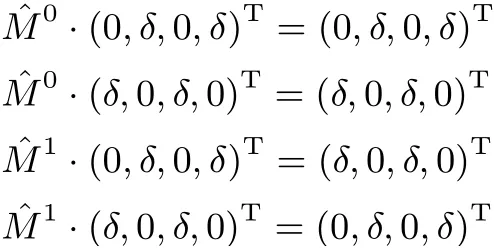
4 7 輪PRINCE 的差分區(qū)分器

由于輪密鑰加和輪常數(shù)加不影響差分, 在下面的分析中我們將忽略這兩個操作. 7 輪PRINCE 可以表示成:

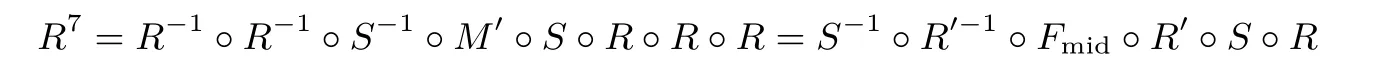
其中R = SR ?M′?S,R′= S ?SR ?M′,Fmid= M′?SR?1?S?1?M′?S ?SR ?M′. 為了計算7 輪PRINCE 在限定輸入和輸出差分集合的差分概率, 我們逐層考慮差分路徑中各個節(jié)點的差分概率. 首先考慮R 層的輸入差分集合

它們經(jīng)過R 層的具體差分路徑如圖4 所示.

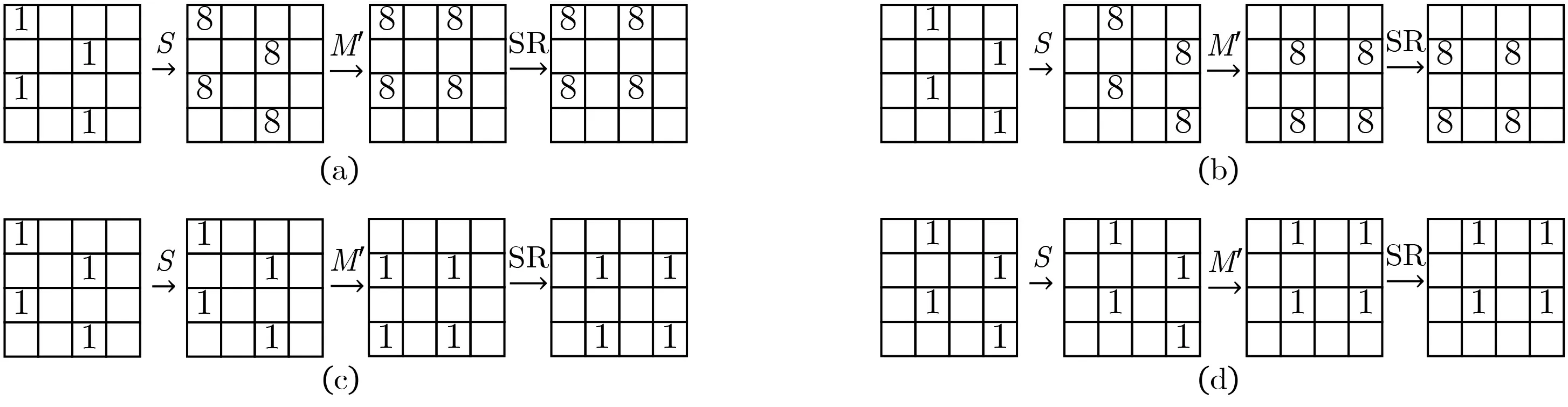
圖4 R 層的4 條差分特征Figure 4 4 differential characteristics of R

由于擴散層中矩陣 ?M0, ?M1具有的特殊性質(zhì), 矩陣DR可以寫成分塊矩陣的形式:

其中

矩陣N 中有12 個值大于2?63, 也就是說我們得到7 輪PRINCE 的12×16 = 192 對概率大于2?63的差分, 由于計算時只使用了部分差分特征, 所以實際的差分概率要比DR7中給出的值更大.

5 8 輪PRINCE 的密鑰恢復(fù)攻擊

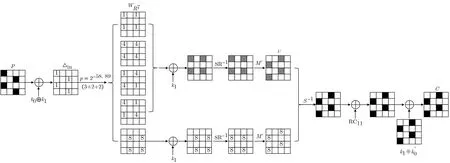
圖5 8 輪PRINCE 密鑰恢復(fù)攻擊(?k)Figure 5 Key recovery attack on 8-round PRINCE(?k)

其中矩陣Z 為一個8×6 的矩陣:

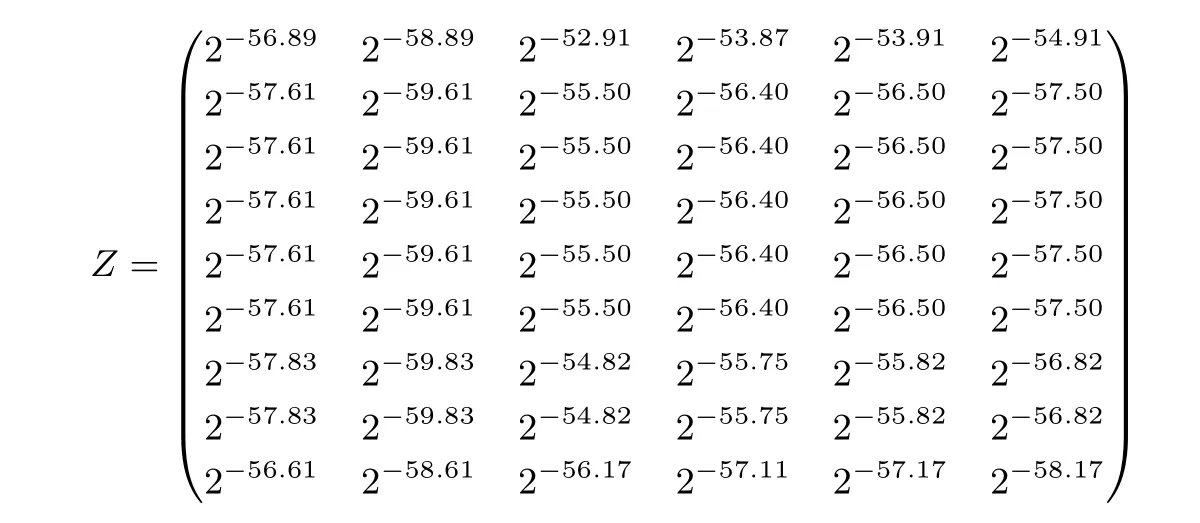
圖6 8 輪PRINCE 密鑰恢復(fù)攻擊(k1)Figure 6 Key recovery attack on 8-round PRINCE(k1)

圖7 應(yīng)用文獻[8] 區(qū)分器攻擊8 輪PRINCEFigure 7 Attack on 8-round PRINCE using distinguisher given in Ref. [8]

6 結(jié)束語

本文利用改進的多重差分技術(shù)給出了目前輪數(shù)最長的7 輪PRINCE 區(qū)分器, 將其與隨機置換區(qū)分需要數(shù)據(jù)復(fù)雜度約為257.89個選擇明文, 計算復(fù)雜度約為256.89次密文異或. 利用此區(qū)分器我們給出了8 輪PRINCE 的密鑰恢復(fù)攻擊, 數(shù)據(jù)復(fù)雜度為261.89個選擇明文, 時間復(fù)雜度為219.68次8 輪加密, 存儲復(fù)雜度為215.21個16 比特計數(shù)器. 相比目前已知的8 輪PRINCE 密鑰恢復(fù)攻擊的結(jié)果, 包括將A.Canteaut 等給出的10 輪攻擊方案減少到8 輪, 本文的時間復(fù)雜度和D×T 復(fù)雜度都是最低的. 能否將本文的攻擊技術(shù)擴展到更高輪數(shù)將是我們后續(xù)研究的方向.