李 全, 徐 松, 王 偉

模糊厭惡下含匯率風險的最優(yōu)投資策略

李 全, 徐 松, 王 偉*

（寧波大學 數(shù)學與統(tǒng)計學院, 浙江 寧波 315211）

研究了模糊厭惡和指數(shù)效用情形下含匯率風險的穩(wěn)健最優(yōu)投資問題. 假定投資者是模糊厭惡且可投資無風險債券、國外股票和國內(nèi)股票3種資產(chǎn), 在最大化終端財富期望效用的目標下, 通過隨機動態(tài)規(guī)劃原理得到相應的HJB(Hamilton-Jacobi-Bellman)方程, 然后通過求解HJB方程和一階最優(yōu)條件得到模糊厭惡和模糊中性2種情形下最優(yōu)投資策略的解析解, 最后給出數(shù)值結(jié)果和經(jīng)濟學解釋. 結(jié)果表明, 模糊厭惡程度和匯率風險對最優(yōu)投資策略影響較大.

模糊厭惡; 匯率風險; 最優(yōu)投資組合

跨國投資是投資者將自己擁有的資金投資于2個或2個以上國家, 因此投資者必須面對本國貨幣與外幣之間的匯率風險. 近年來, 隨著國際金融環(huán)境波動和貿(mào)易戰(zhàn)升級, 匯率波動愈加頻繁, 這也直接影響了跨國投資的資產(chǎn)配置. 由于匯率風險在跨國投資等涉及外匯的業(yè)務中扮演重要角色, 因此研究匯率風險下的最優(yōu)投資問題是金融市場的一個實際問題, 具有重要意義.

在匯率風險下的最優(yōu)投資研究中, 閆偉等[1]利用跳躍擴散過程描述了市場匯率動態(tài), 研究了均值-方差模型下的連續(xù)時間最優(yōu)投資組合. 費為銀等[2-3]認為企業(yè)進行跨國投資時, 會面臨奈特不確定, 即對要投資國家的經(jīng)濟變量無法準確知道,為此研究了奈特不確定和存在匯率風險時的最優(yōu)投資和稅收政策; 研究假定匯率動態(tài)滿足幾何布朗運動,但市場中可投資的風險資產(chǎn)滿足跳擴散過程, 在終端財富效用最大化準則下, 利用HJB (Hamilton-Jacobi-Bellman)方程得到了最優(yōu)投資策略. Guo等[4]考慮一家保險公司可投資國內(nèi)外市場中的無風險債券和風險資產(chǎn), 首次研究了匯率風險下保險公司的最優(yōu)投資和再保險, 利用擴散過程來近似保險公司索賠過程, 從而降低了模型的復雜性. 黃嬋等[5]在文獻[4]基礎上,進一步考慮了保險公司的索賠過程滿足經(jīng)典的跳擴散模型, 研究了保險公司在指數(shù)效用下的最優(yōu)投資和最優(yōu)再保險策略. 與文獻[1]和文獻[3]不同,邢鈺等[6]考慮了匯率動態(tài)滿足跳擴散過程, 研究了常相對風險厭惡效用(CRRA)下的最優(yōu)投資, 且假定匯率和風險資產(chǎn)動態(tài)都滿足跳擴散過程, 并通過求解偏微分方程得到了最優(yōu)投資策略的近似解.

上述研究都是在模糊中性環(huán)境下開展, 而實際復雜多樣的市場因素會影響模型的誤定, 投資者會擔心模型的誤定對投資策略產(chǎn)生較大影響, 因此需要尋求穩(wěn)健的投資決策. Ellsberg[7]第一個指出大多數(shù)人都是模糊厭惡的, 大量實證也證明模糊厭惡影響了投資者的投資行為[8-9]. Maenhout[10]首次將模糊厭惡的概念應用到資產(chǎn)定價和最優(yōu)投資組合領域, 并考慮了模糊厭惡情形下最優(yōu)投資和資產(chǎn)定價問題. Branger等[11]假定市場中的風險資產(chǎn)價格滿足跳擴散模型, 研究了不同程度的模糊厭惡對最優(yōu)投資策略的影響. Zeng等[12]假定市場中存在可投資的歐式衍生產(chǎn)品, 研究了在模糊厭惡環(huán)境下確定繳費型養(yǎng)老金的最優(yōu)投資問題. Sun等[13]假設保險公司的盈余過程服從經(jīng)典的Cramér-Lundberg模型, 得到了模糊厭惡下穩(wěn)健最優(yōu)投資和再保險策略的解析解. Zhang等[14]考慮了金融市場中存在可投資的信用債券情形, 研究了模糊厭惡環(huán)境下穩(wěn)健最優(yōu)投資和比例的再保險. Wang等[15]研究了2家競爭性保險公司之間非零和隨機微分博弈問題, 利用隨機動態(tài)規(guī)劃和驗證定理得到了穩(wěn)健的納什均衡再保險和投資策略. 然而, 以上文獻都沒有在模糊厭惡環(huán)境下考慮匯率風險的影響, 而實際上投資者的模糊厭惡態(tài)度和匯率風險都會影響其對跨國企業(yè)的投資選擇. 因此, 考慮模糊厭惡下含匯率風險的最優(yōu)投資組合具有重要意義.

本研究同時考慮金融市場存在匯率風險且投資者是模糊厭惡的, 利用幾何布朗運動刻畫匯率動態(tài),研究模糊厭惡下含匯率風險的最優(yōu)投資, 并利用隨機動態(tài)規(guī)劃原理得到了最優(yōu)投資策略的解析解, 且給出了數(shù)值算例和經(jīng)濟學解釋.

1 金融市場模型

1.1 金融資產(chǎn)的價格動態(tài)

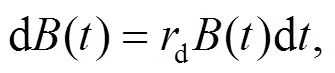
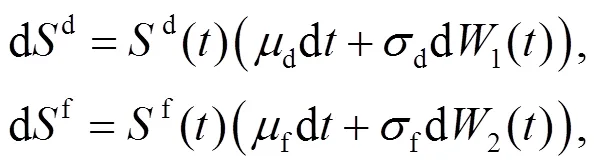
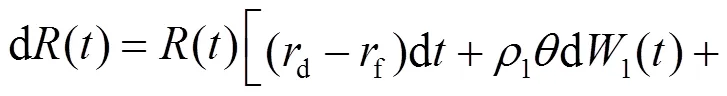
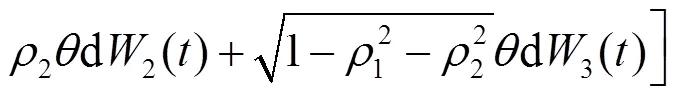
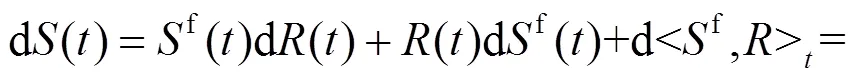
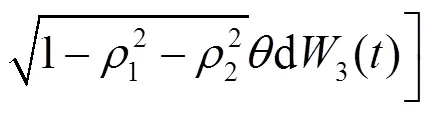
1.2 財富過程

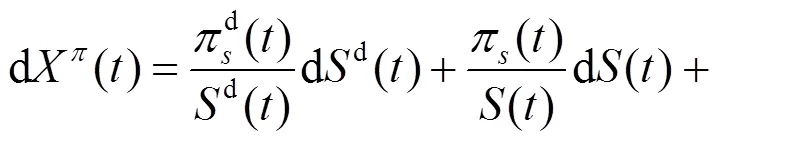
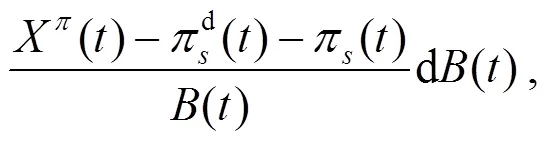
將式(1)~(3)代入方程(4), 整理可得:

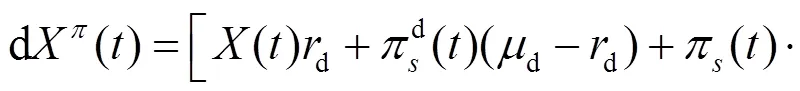
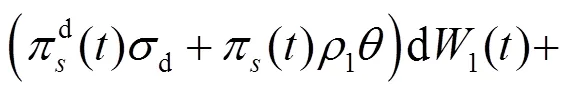
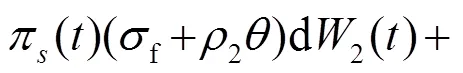
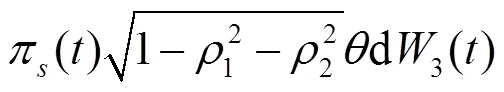
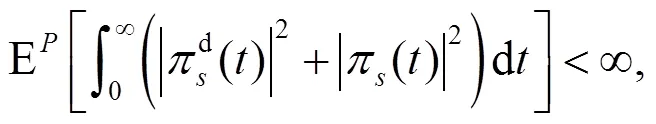
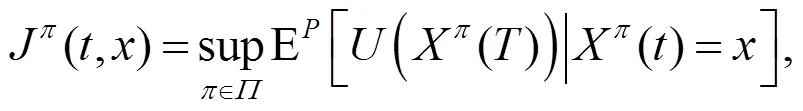
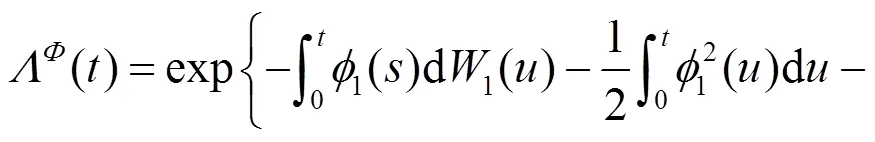
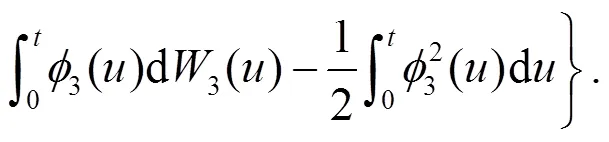
由哥薩諾夫定理可知:

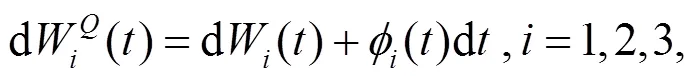
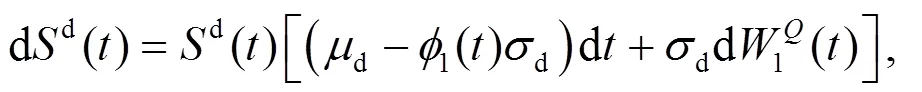
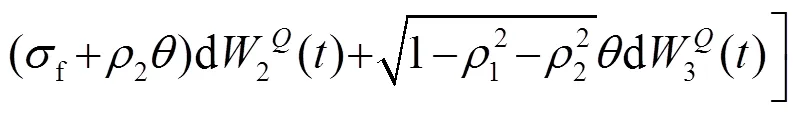
結(jié)合式(6), 投資者財富動態(tài)過程式(5)可表示為:

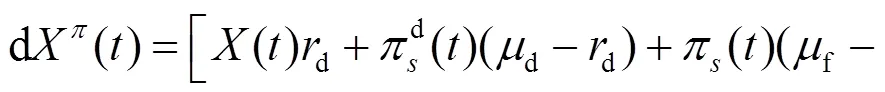
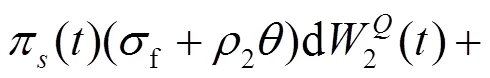
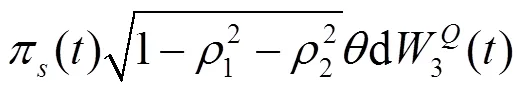
2 指數(shù)效用下的最優(yōu)投資策略

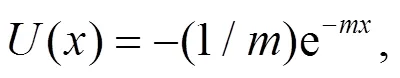
采用文獻[10]方法, 選取最壞情形下的最優(yōu)投資策略, 使得投資者的終期財富的期望效用達到最大化,其最優(yōu)化問題為:

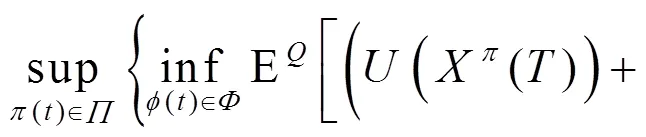
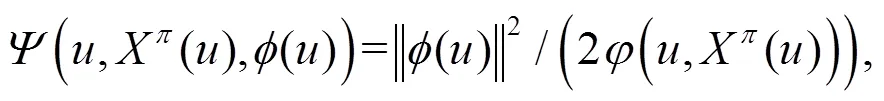
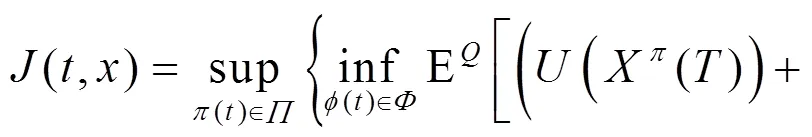
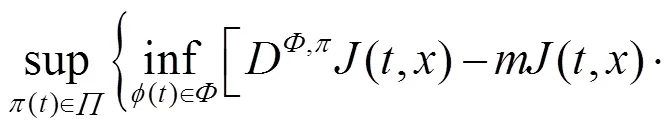
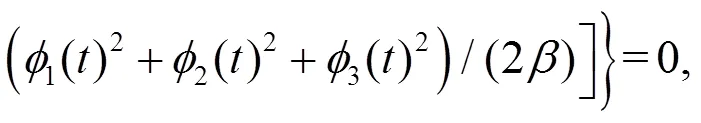
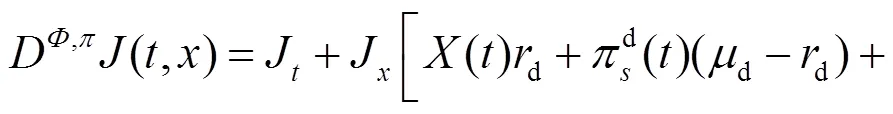
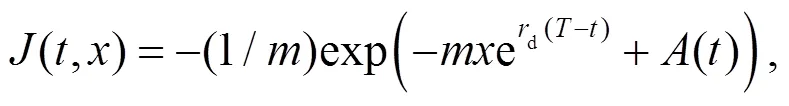
其中:

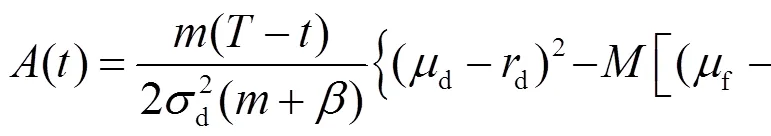
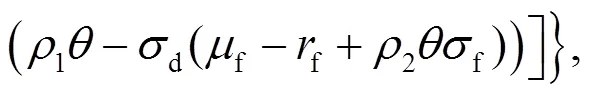
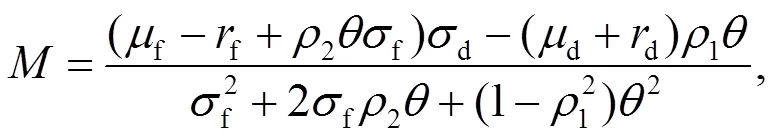
投資者的最優(yōu)投資策略為:

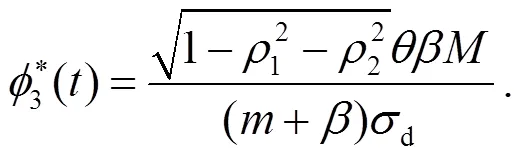
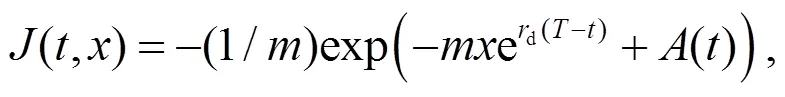
為計算方便, 將HJB方程寫為:

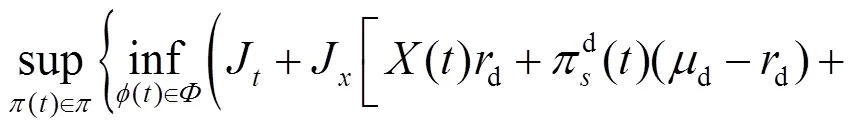
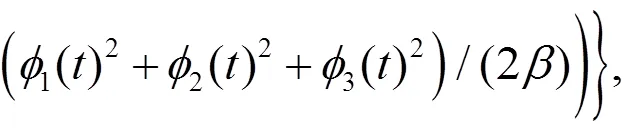
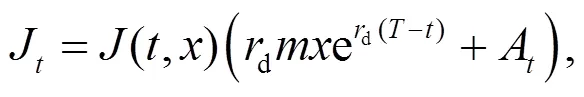
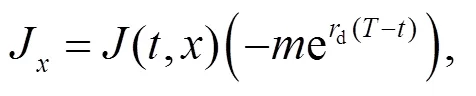
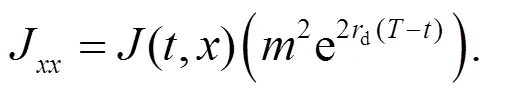
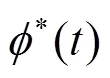
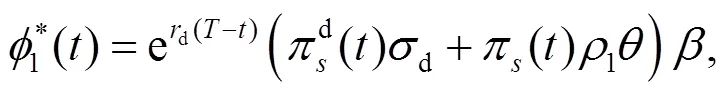
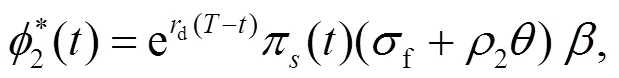
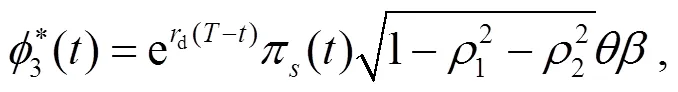
將式(15)~(17)代入式(13), 得到:

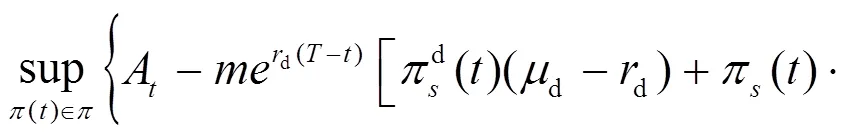
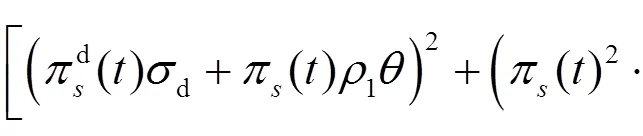
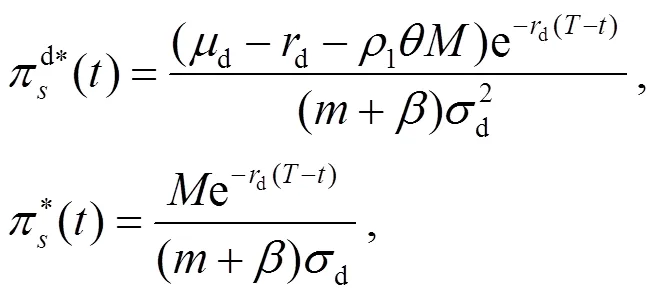
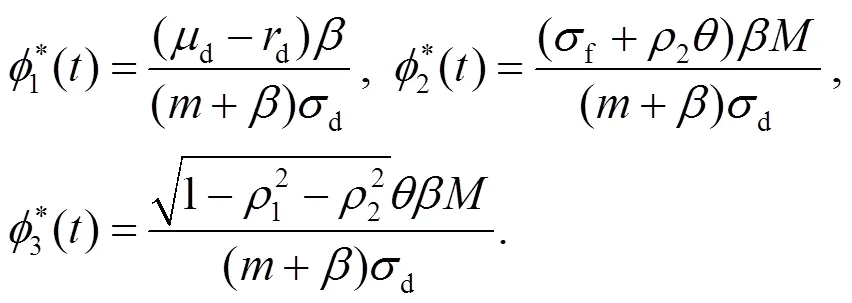
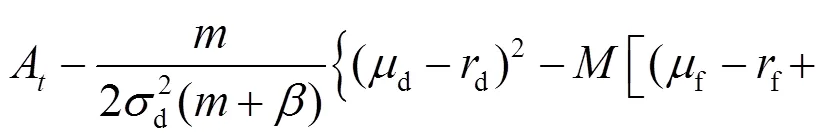
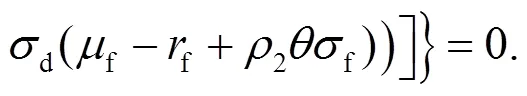
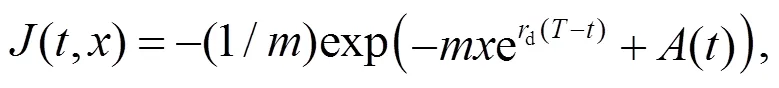
其中:

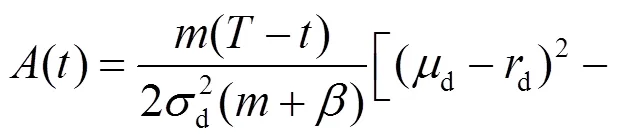
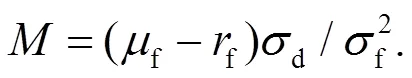
另外, 投資者的最優(yōu)投資策略為:

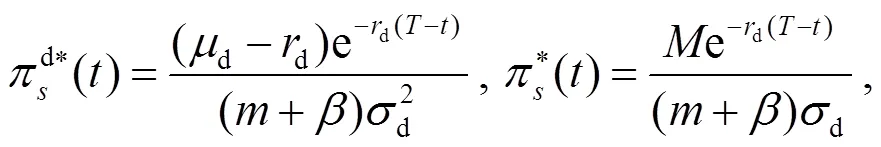
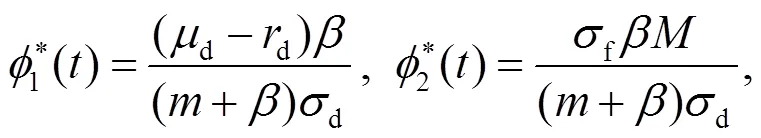
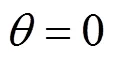
注2 當投資者為模糊中性, 且效用函數(shù)滿足指數(shù)效用時, 方程(9)有如下解的形式:

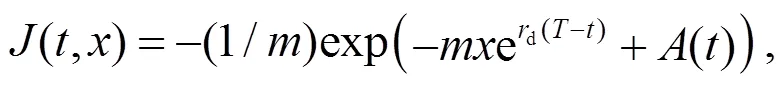
其中:

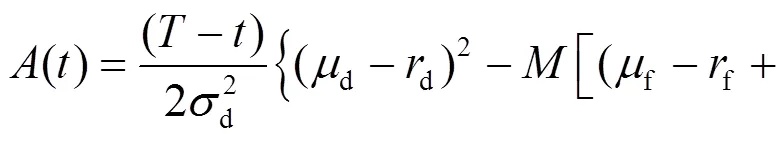
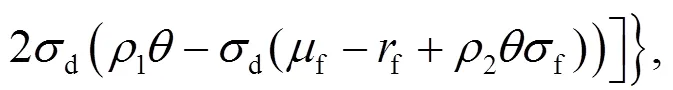
得到投資者的最優(yōu)投資策略為:

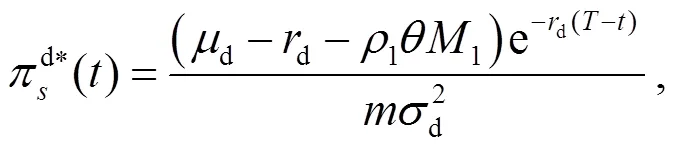
注3 當市場不存在匯率風險, 投資者為模糊中性且效用函數(shù)滿足指數(shù)效用時, 方程(9)滿足:

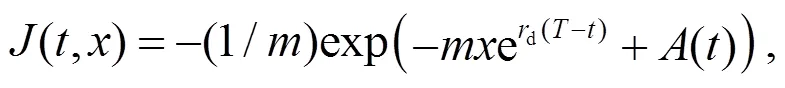
其中:

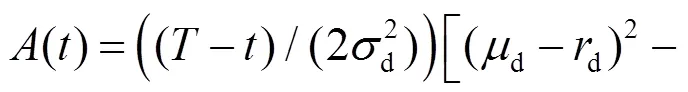
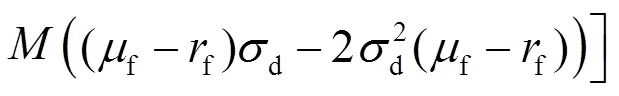
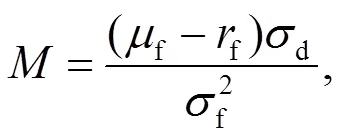
且投資者的最優(yōu)投資策略為:

3 數(shù)值算例

表1 相關參數(shù)取值

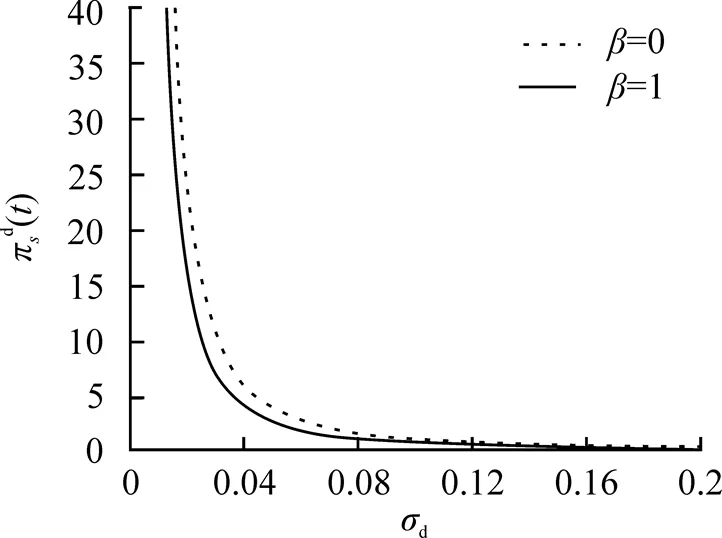
圖1 參數(shù)對最優(yōu)投資策略的影響

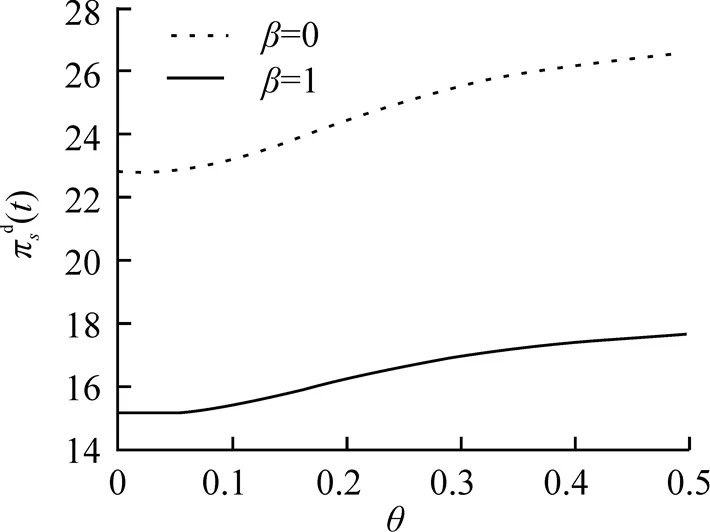
圖2 參數(shù)對最優(yōu)投資策略的影響

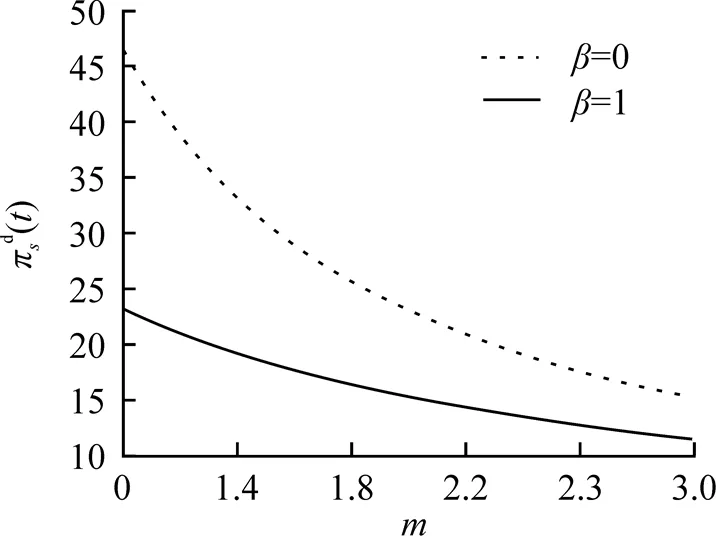
圖3 參數(shù)對最優(yōu)投資策略的影響

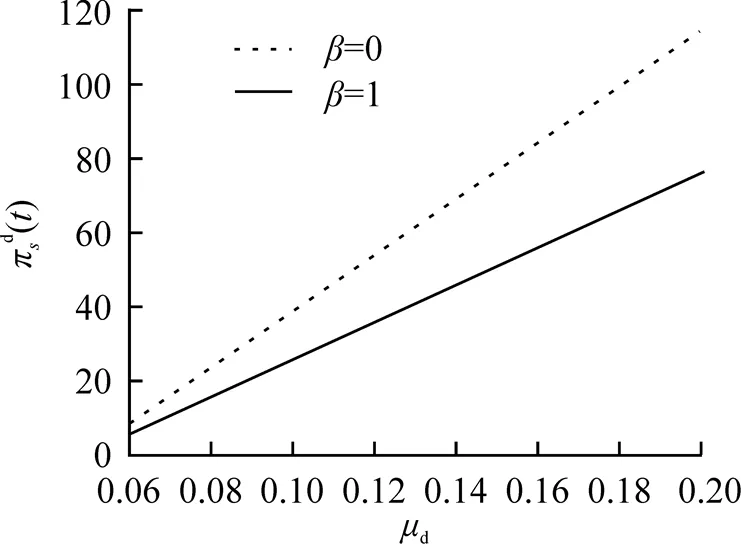
圖4 參數(shù)對最優(yōu)投資策略的影響

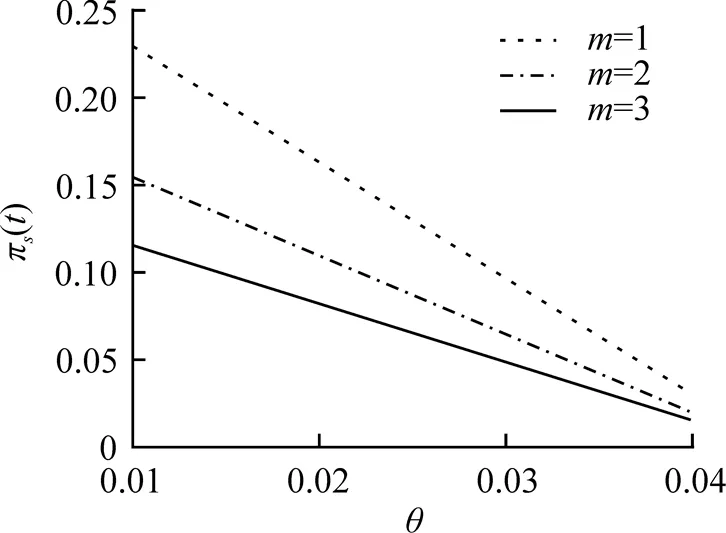
圖5 參數(shù)m和θ對最優(yōu)投資策略的影響

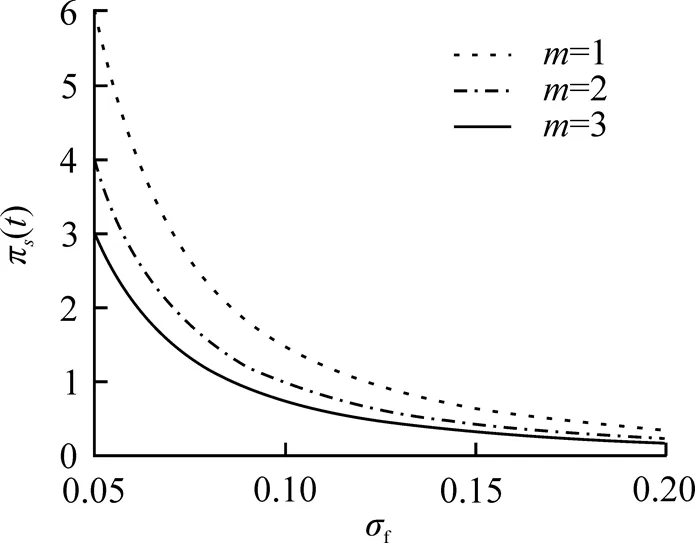
圖6 參數(shù)m和對最優(yōu)投資策略的影響

4 結(jié)語

本文研究了當金融市場中存在匯率風險和投資者為模糊厭惡時的最優(yōu)投資組合, 得到了最優(yōu)投資策略的解析解. 研究結(jié)果表明: (1)投資者為模糊厭惡時投資策略比模糊中性時更為保守, 即相對于風險資產(chǎn), 投資者更愿意投資無風險資產(chǎn); (2)匯率風險的波動率越大, 投資者越會減少對國外風險資產(chǎn)的投資, 加大對國內(nèi)風險資產(chǎn)的投資, 表明模糊厭惡和匯率風險對最優(yōu)投資策略影響較大. 后續(xù)將進一步研究當風險資產(chǎn)和匯率動態(tài)滿足跳擴散過程, 且投資者為模糊厭惡時的穩(wěn)健最優(yōu)投資問題.

[1] 閆偉, 李樹榮. 帶有匯率因素的不連續(xù)價格過程的最優(yōu)投資組合研究[J]. 運籌與管理, 2008, 17(3):134-139.

[2] 費為銀, 高貴云, 夏登峰. 考慮匯率變動的跨國直接投資和稅收政策研究[J]. 系統(tǒng)工程學報, 2015, 30(6): 746-754; 864.

[3] 費為銀, 何丹丹, 張偉. 跳擴散下匯率變動的外商直接投資問題研究[J]. 系統(tǒng)工程理論與實踐, 2015, 35(2): 283-290.

[4] Guo C, Zhuo X Y, Constantinescu C, et al. Optimal reinsurance-investment strategy under risks of interest rate, exchange rate and inflation[J]. Methodology and Computing in Applied Probability, 2018, 20(4):1477-1502.

[5] 黃嬋, 王偉, 溫利民. 匯率風險和方差保費原理準則下最優(yōu)投資和再保險策略[J]. 應用概率統(tǒng)計, 2019, 35(5): 508-524.

[6] 邢鈺, 徐玉華, 王曉燕. 匯率帶有跳躍情形下的外商直接投資的最優(yōu)投資組合問題[J]. 數(shù)學的實踐與認識, 2020, 50(9):284-295.

[7] Ellsberg D. Risk, ambiguity, and the savage axioms[J]. The Quarterly Journal of Economics, 1961, 75(4):643-669.

[8] Bossaerts P, Ghirardato P, Guarnaschelli S, et al. Ambiguity in asset markets: Theory and experiment[J]. The Review of Financial Studies, 2010, 23(4):1325-1359.

[9] Dimmock S G, Kouwenberg R, Mitchell O S, et al. Ambiguity aversion and household portfolio choice puzzles: Empirical evidence[J]. Journal of Financial Economics, 2016, 119(3):559-577.

[10] Maenhout P J. Robust portfolio rules and asset pricing[J]. Review of Financial Studies, 2004, 17(4):951-983.

[11] Branger N, Larsen L S. Robust portfolio choice with uncertainty about jump and diffusion risk[J]. Journal of Banking & Finance, 2013, 37(12):5036-5047.

[12] Zeng Y, Li D P, Chen Z, et al. Ambiguity aversion and optimal derivative-based pension investment with stochastic income and volatility[J]. Journal of Economic Dynamics and Control, 2018, 88:70-103.

[13] Sun Z Y, Zheng X X, Zhang X. Robust optimal investment and reinsurance of an insurer under variance premium principle and default risk[J]. Journal of Mathematical Analysis and Applications, 2017, 446(2): 1666-1686.

[14] Zhang Q, Chen P. Robust optimal proportional reinsurance and investment strategy for an insurer with defaultable risks and jumps[J]. Journal of Computational and Applied Mathematics, 2019, 356:46-66.

[15] Wang N, Zhang N, Jin Z, et al. Robust non-zero-sum investment and reinsurance game with default risk[J]. Insurance: Mathematics and Economics, 2019, 84:115- 132.

Optimal investment strategies with exchange rate risk and ambiguity aversion

LI Quan, XU Song, WANG Wei*

( School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )

The robust optimal investment problem with exchange rate risk is studied in the case of ambiguity aversion and exponential utility. We assume that investors are those of ambiguity aversion and plan on investing in risk-free bonds, foreign stocks and domestic stocks. With the goal of maximizing the expected utility of terminal wealth, the corresponding HJB equation is obtained using the principle of stochastic dynamic programming, and then the analytical solution of the optimal investment strategies with ambiguity aversion and ambiguity neutrality are obtained by using the first-order optimal conditions and solving the HJB equation. Finally, numerical results and economic explanations are given. The numerical results show that the degree of ambiguity aversion and exchange rate risk impose a great influence on the optimal investment strategies.

ambiguity aversion; exchange rate risk; optimal portfolio

O211.9

A

1001-5132（2021）02-0102-07

2020?07?17.

寧波大學學報（理工版）網(wǎng)址: http://journallg.nbu.edu.cn/

教育部人文社科基金（18YJC910012）; 浙江省教育廳科研項目（Y201430940）; 寧波市自然科學基金（202003N4144）.

李全（1996－）, 女, 貴州畢節(jié)人, 在讀碩士研究生, 主要研究方向: 金融數(shù)學. E-mail: 2441237380@qq.com

王偉（1982－）, 男, 安徽安慶人, 博士/教授, 主要研究方向: 金融數(shù)學. E-mail: wangwei2@nbu.edu.cn

（責任編輯 史小麗）