Linear gyrokinetic simulations of reversed shear Alfvén eigenmodes and ion temperature gradient modes in DIII-D tokamak
Hongyu WANG(王虹宇),Pengfei LIU(劉鵬飛),Zhihong LIN(林志宏) and Wenlu ZHANG (張文祿)
1 Fusion Simulation Center, Peking University, Beijing 100871, People’s Republic of China
2 Department of Physics and Astronomy, University of California, Irvine, CA 92697, United States of America
3 Institute of Physics, Chinese Academy of Sciences, Beijing 100190, People’s Republic of China
Abstract Global linear gyrokinetic simulations using realistic DIII-D tokamak geometry and plasma profiles find co-existence of unstable reversed shear Alfvén eigenmodes (RSAE) with low toroidal mode number n and electromagnetic ion temperature gradient (ITG) instabilities with higher toroidal mode number n.For intermediate n = [10, 12], RSAE and ITG co-exist and overlap weakly in the radial domain with similar growth rates but different real frequencies.Both RSAE and ITG growth rates decrease less than 5% when compressible magnetic perturbations are neglected in the simulations.The ITG growth rates increase less than 7%when fast ions are not included in the simulations.Finally, the effects of trapped electrons on the RSAE are negligible.
Keywords:fast ions,gyrokinetic simulation,reversed shear Alfvén eigenmodes,microturbulence
1.Introduction
Energetic particle(EP)confinement is a key physical issue for burning plasma experiment in ITER[1,2]since ignition relies on self-heating by energetic fusion products[3],i.e.α-particles.The EP population in current tokamaks can be produced by auxiliary heating such as neutral beam injection [4] and radio frequency heating[5].EP pressure gradients can readily excite mesoscale EP instabilities such as the Alfvén eigenmodes(AE)[6], which can drive large EP transport, degrade overall plasmas confinement, and threaten the machines’ integrity [7].Because EP constitutes a significant fraction of the plasma energy density, EP could influence thermal particle dynamics including the microturbulence [8, 9] responsible for turbulent transport of thermal particles and the macroscopic magnetohydrodynamic (MHD) modes potentially leading to disastrous disruptions [10].In return, microturbulence and MHD modes can affect EP confinement [11, 12].
Thanks to recent progress in developing comprehensive EP simulation codes and understanding basic EP physics,gyrokinetic turbulence simulation has been successfully established as a necessary paradigm shift for studying EP confinement [13-16].Integrated simulation incorporating multiple physical processes and disparate temporal-spatial scales becomes available now to address new challenges in the EP physics such as the coupling of EP-driven AE turbulence with thermal particles-driven microturbulence and macroscopic MHD modes.The fully self-consistent gyrokinetic turbulence simulation needs to treat both EP and thermal particles on the same footing to address the kinetic effects of thermal particles and the cross-scale couplings between microturbulence, EP turbulence, and MHD modes.
Toward such an integrated simulation of EP coupling with thermal particles, we have initiated comprehensive simulations of turbulent transport by low frequency electromagnetic instabilities (including AE and microturbulence) in a reversed shear geometry of DIII-D tokamak with fast ions[17]by using the gyrokinetic toroidal code(GTC)[18].GTC has been extensively verified and validated for global simulations of AE [13-16, 19] and microturbulence [11, 18,20-22].As the first step in the integrated simulations of EP,we study the linear properties of these electromagnetic instabilities, which could provide a foundation for the next step of nonlinear simulations of multiple physical processes.
In this paper, linear global GTC simulations using realistic DIII-D magnetic geometry and plasma profiles with kinetic electrons, thermal ions and fast ions find co-existence of unstable reversed shear Alfvén eigenmodes (RSAE) with low toroidal mode number <n10 and ion temperature gradient (ITG) instabilities with higher toroidal mode numbern>12.For intermediate toroidal modesn=[10,12],RSAE and ITG eigenmodes overlap weakly in the radial domain with similar growth rates but different real frequencies.The RSAE polarization is very close to ideal Alfvénic state,while the ITG polarization is closer to electrostatic but with significant magnetic perturbations.
Our simulations represent the first gyrokinetic study for the effects of compressible magnetic perturbations δB||on the RSAE in this DIII-D experiment.GTC simulations with δB||have been verified for ITG, collisionless trapped electron mode, and kinetic ballooning mode [23, 24].Although many gyrokinetic codes have the capability for including δB||in the simulations of microturbulence, most of gyrokinetic simulations of RSAE neglect δB||[9, 13, 16, 25-27].On the other hand,most of hybrid MHD-gyrokinetic codes do not separate parallel and perpendicular magnetic perturbations [13, 16,28-30].Therefore, the effects of δB||on RSAE are not well understood.The δB||can be important for low frequency instabilities since it cancels out the stabilizing ‘drift-reversal’effects of the guiding center ?Bdrifts associated with the perpendicular diamagnetic current in finite-β plasmas [31].Gyrokinetic flux-tube simulations using GS2 code [32] for ITG in a simples-α geometry find that the ITG growth rate decreases by a factor of 3 when δB||is neglected in the simulations.However, global GTC simulations using similar geometry and plasma β find that the ITG growth rate decreases less than 5% when δB||is neglected in the simulations [24].In the current GTC simulations using realistic DIII-D magnetic geometry and plasma profiles, both RSAE and ITG growth rates decrease less than 5% when δB||is neglected in the simulations.Furthermore, GTC simulations find that the effects of trapped electrons on the RSAE are negligible.
Our simulations also clarify the effects of fast ions on the ITG in this DIII-D experiment.It is well-known that the adiabatic responses of electrons and fast ions can have stabilizing effects on the ITG due to the finite-β stabilization[33]and that fast ion drift-bounce and precessional resonances[6,34,35]can stabilize or destabilize low frequency drift-Alfvén instabilities,depending on specific plasma parameters.In the current GTC simulations using realistic DIII-D magnetic geometry and plasma profiles,the ITG growth rate increases less than 7% when fast ions are not included in the simulations.Finally, GTC simulations find that the ITG eigenmodes become stable if electrons are assumed to be adiabatic, i.e.by neglecting kinetic effects of trapped electrons.
The rest of the paper is organized as follows.In section 2,GTC electromagnetic simulation model with compressible magnetic perturbations δB||is described.The simulation results are discussed in section 3.The conclusions are provided in section 4.
2.Gyrokinetic electromagnetic simulation model
By means of parallel symplectic gyrocenter model [36], the nonlinear gyrokinetic equation used in GTC to study low frequency mode could be written as [24, 37],
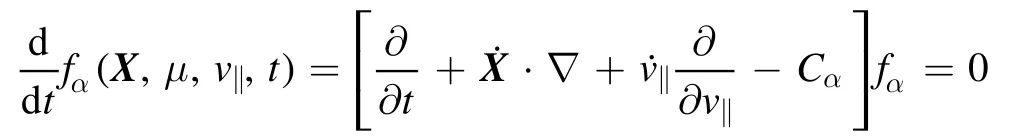
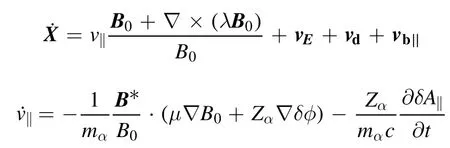
In order to reduce the particle noise in simulations,δf-method [38] is used for thermal ions and fast ions, by decomposing the distribution functionαfof species α into an equilibrium partαf0and a perturbed partδαf, i.e.The equilibrium part is defined by:
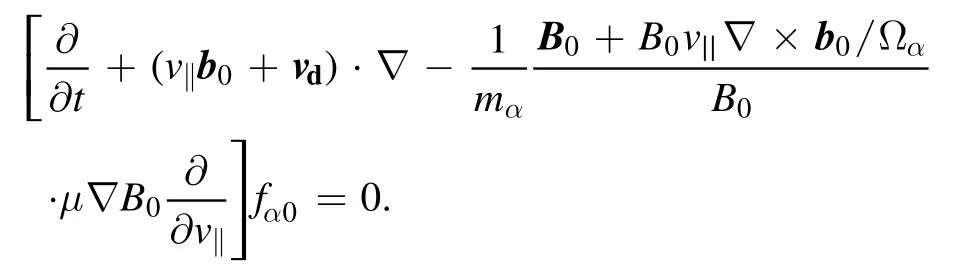
The perturbed part is solved by using a particle weight variablewhich satisfies:

Particle densityαnand parallel velocity‖αuare moments of distribution functions in velocity space:
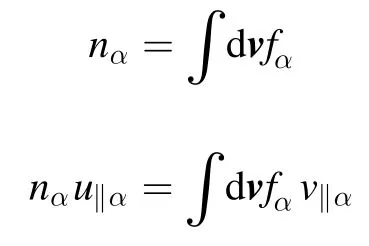
where
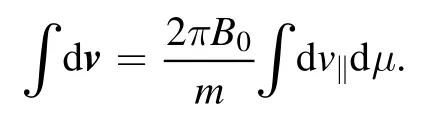
The electron dynamics is described by the fluid-kinetic hybrid model[37],which separates the electron response into a dominant adiabatic part and a higher order nonadiabatic part due to the small electron ion mass ratio,i.e.The equilibrium distributionfe0is defined by equation(4).The adiabatic partis defined as:
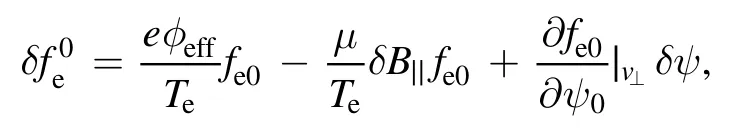
where,
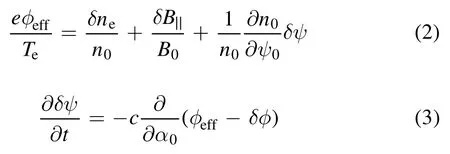
ψ,θ,ζare, respectively, poloidal flux, poloidal angle, and toroidal angle in magnetic coordinates,andis the magnetic field line label.The Clebsch representation for the toroidal magnetic field isin which the magnetic flux perturbationδψis calculated by assumingEffective scalar potential is
The nonadiabatic partδheis solved by using an electron weightwhich satisfies:
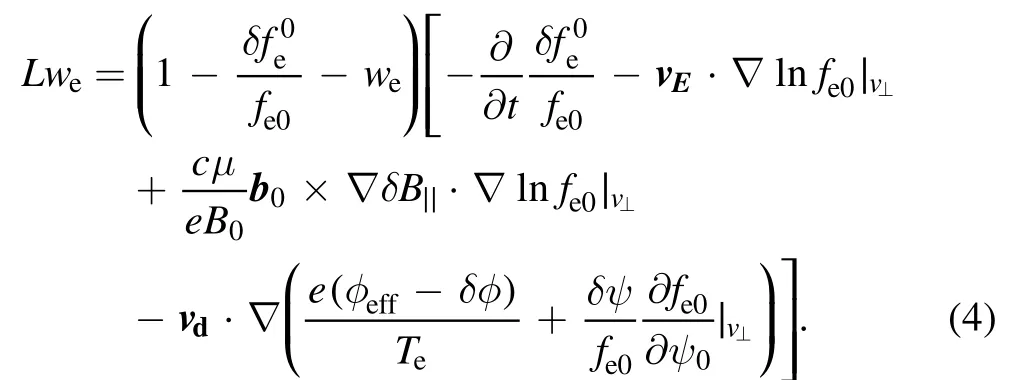
The perturbed electron density is calculated by the continuity equation:

where
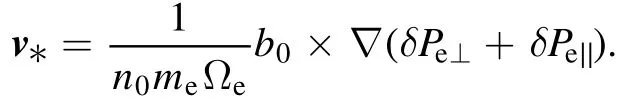
The electron pressure is defined as:

and the electron parallel flow is calculated from the Ampere’s law:
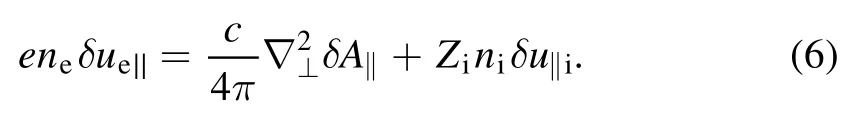
These electron equations are closed by the gyrokinetic Poisson’s equation, perpendicular Ampere’s law, and Ohm’s law forδφ,δB∣∣andδA∣∣, respectively,
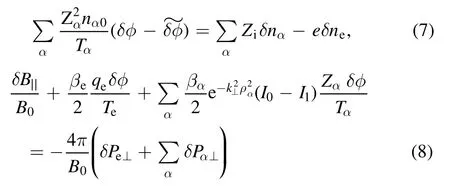
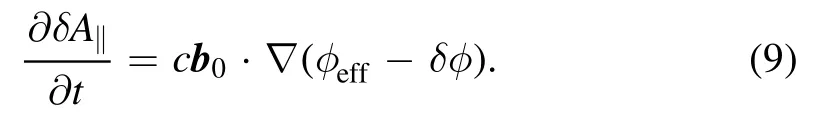
3.Simulation results
In this section,we use the GTC model described in section 2 to simulate low frequency electromagnetic instabilities in the DIII-D tokamak shot #159243 att= 805 ms [17].GTC simulations use the same magnetic geometry and plasma profiles of DIII-D as those in a verification and validation benchmark of RSAE [16].The density and temperature profiles for the electrons,thermal ions,and fast ions are shown in figure 1(a).For simplicity, Maxwellian distribution function is assumed for both fast ions and thermal particles in this work (effects of slowing-down distribution function will be studied in the future work).This is a reversed shear discharge with the minimum safety factor of qmin=2.94at the poloidal flux functionψ = 0.24ψX(ψXis the poloidal flux function at the magnetic separatrix) as shown in figure 1(b).Some key plasma parameters are as follows:major radius R0=1.72 m,on axis electron temperature Te=1.69 keV,density ne=3.29 ×1019m-3,magnetic field B0=1.99 T,and total beta 0.9%.Atψ = 0.68ψX,the characteristic lengths of density and temperature gradients areandwithand the minor radiusris defined as the distance from magnetic axis on the outer mid-plane.The boundaries of the radial simulation domain areandfor the ITG simulations,andfor the RSAE simulations.The simulation time step size is1.24 × 105s?1.For linear simulations,we use 250 radial grid points, 1500 poloidal grid points, 32 parallel grid points, and 100 particles per cell each for electrons, thermal ions and fast ions.
The fast ion density and temperature gradients have been shown [16] to drive an unstable RSAE near qmin.The strong temperature gradients of thermal ions and electrons are expected to excite the ITG instabilities.To study these instabilities,we have performed a series of linear simulations,each with a single toroidal mode numbern.We have found unstable toroidal modes forn>2.The branches of these modes can be identified by the frequencies and polarizations.The real frequencies and growth rates for these unstable modes are shown in figure 2(a).Forn= [3, 9], the instabilities are dominated by the RSAE driven by the fast ions.Forn≥10, the instabilities are dominated by the ITG excited by the thermal ions and electrons.A sub-dominant RSAE can also be identified forn= [10, 12], where the RSAE growth rates are smaller than the ITG growth rates.Both RSAE and ITG propagate in the ion diamagnetic direction (i.e.negative real frequencies).The RSAE real frequency increases with the toroidal mode numbernuntiln= 8, where it reaches a plateau.The RSAE real frequencies are much larger than the growth rates,indicating a resonant excitation by the fast ions.The most unstable RSAE withn= 4 (which corresponds to kθρf=0.51) has a growth rate ofγ4= 3.24 × 104s-1and real frequencyThe ITG growth rates are comparable to the real frequencies for all thenmodes,indicating mostly non-resonant instabilities due to the strong temperature gradients of the thermal ions and electrons.The most unstable ITG withn= 20 (which corresponds tohas a growth rate ofand real frequency104s-1, i.e.γ20~ ω20.The RSAE and ITG growth rates decrease for highernmodes due to the finite Larmor radius effects of the fast ions and thermal ions, respectively.
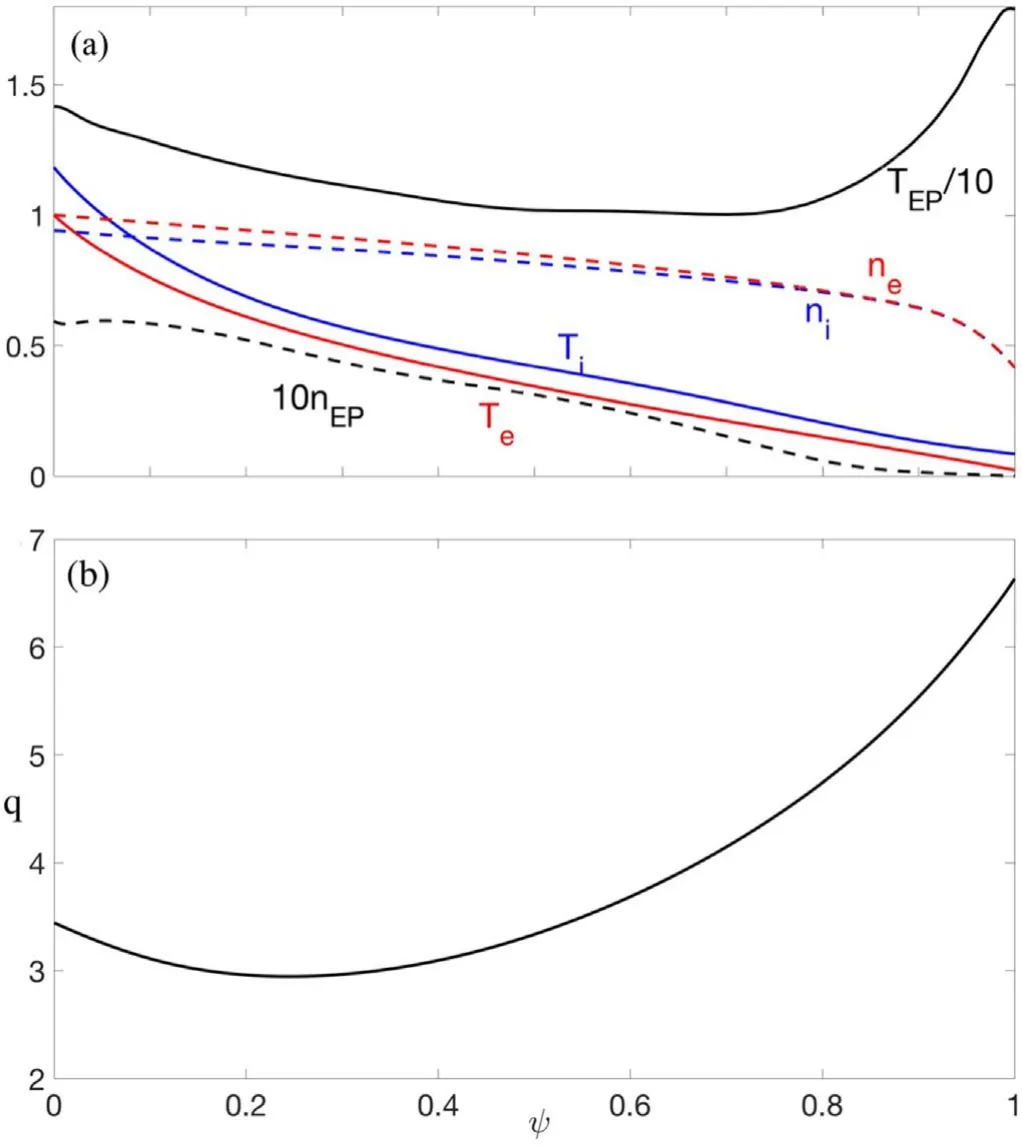
Figure 1.Equilibrium plasma profiles of DIII-D shot#159243 at 805 ms.(a) Radial profiles of densities (dashed lines, normalized to the electron on axis value n0 = 3.29 × 1019 m?3)and temperatures(solid lines,normalized to the electron on-axis value Te0 = 1.69 keV)for the electron(red),thermal ion(blue),and fast ion(black).Fast ion density is multiplied by 10 and temperature divided by 10.(b) Radial profile of safety factor q with qmin = 2.94 at poloidal flux functionψ = 0.24 ψX .Data are taken from [16].
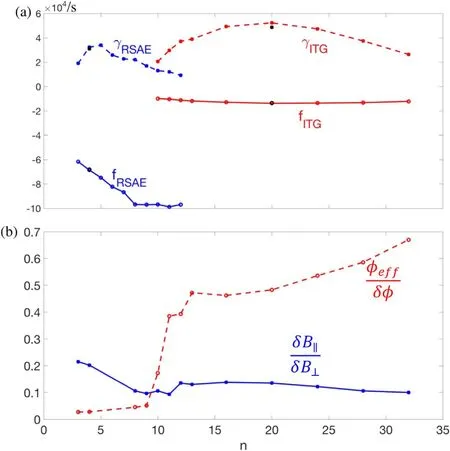
Figure 2.Dispersion relation and polarization: toroidal mode number n dependence of (a) growth ratesγ (dashed lines) and frequencies f =ω /2π (solid lines)for RSAE(blue)and ITG(red), and(b)ratio of volume-averaged δ B‖ /δB ⊥ (blue solid line)and φe ff /δφ(red dashed line).Black cycles and black squares are, respectively, frequencies and growth rates from simulations without δB‖.
Besides the fact that the RSAEs have much higher frequencies than the ITGs,they have different polarizations.The RSAE polarization is Alfvénic, where the inductive parallel electric fields are nearly canceled out by the electrostatic parallel electric fields, i.e.On the other hand, the ITG polarization is electrostatic, where the net parallel electric fields are dominated by the electrostatic components, i.e.φeff~δφ.The ratio of effective potential over electrostatic potentialis shown in figure 2(b).For toroidal modesn= [3, 9], the ratiowhich indicates that unstable RSAE is indeed Alfvénic.The ratioincreases for larger toroidal mode numbern.Forn> 12, the ratiowhich indicates that ITG instability is closer to electrostatic but with significant electromagnetic perturbations.
The generation and effects of compressible magnetic perturbations have been studied.The ratio of perturbed parallel magnetic field over perturbed perpendicular magnetic fieldis shown in figure 2(b).For the ITG,15%, indicating that∣∣δBis not significantly generated by the ITG withβ= 0.9%.The ratioslightly increases for RSAE with smallernwithforn= 3 and 4,indicating that the effects of∣∣δBis more strongly generated by the RSAE.Overall, the effects of∣∣δBare not important for both RSAE and ITG since the growth rates only decrease less than 5% and the frequencies barely change when∣∣δBis removed in the simulation ofn= 4 andn= 20 modes, as shown in figure 2(a).We have also studied the effects of fast ions on the ITG and found that the growth rate and frequency of then= 20 ITG increase by less than 7%when the fast ions are not included in the simulations.
We have also studied the effects of trapped electrons on the RSAE and found that then= 4 RSAE growth rate decreases by less than 1% when trapped electrons are not included in the simulations.On the other hand, GTC simulations find that the ITG mode in this DIII-D discharge becomes stable if electrons are adiabatic, i.e.when kinetic effects of trapped electrons are neglected.
The eigenmode structures for toroidal mode numbersn= 4 andn= 10 are compared in figure 3.The perturbed electrostatic potentialδφand parallel vector potential‖δAfor then= 4 RSAE in figures 3(a)and(b)are localized near theqminflux surface with a narrow radial width.The RSAE structure is weakly ballooning and the radial symmetry is broken, i.e.forming triangular shapes due to the non-perturbative effects of fast ions [13, 15, 16, 41].The phase shift betweenδφand‖δAis close to /π2 as expected for the shear Alfvén wave.The structures of the perturbed electrostatic potentialδφand parallel vector potential‖δAfor then= 10 mode in figures 3(c) and (d) are much more complicated due to the co-existence of RSAE and ITG with similar growth rates.In addition to the RSAE mode still visible around the flux surface withqmin,the ITG modes appear in both positive shear (outer) and negative shear (inner) regions [42].The growth rates of these three modes are similar, however, the frequencies are quite different: the RSAE frequency is much larger than that of the ITG in the outer region(positive shear),as shown in figure 2(a).The ITG in the inner region(negative shear)has the smallest frequency,which is much smaller than the growth rate.Compared to then= 4 RSAE, the weakern= 10 RSAE has a stronger ballooning structure.The ITG modes are also strong ballooning.The phase shift betweenδφand‖δAis close to /π2 for both RSAE and ITG eigenmodes.These linear RSAE and ITG eigenmodes overlap weakly in the radial domain.In the future study, we will study the nonlinear interactions of these RSAE and ITG eigenmodes.The spatial overlap of these modes could be even stronger due to turbulence spreading in radial domain [43].

Figure 3.Poloidal mode structures of(a)perturbed electrostatic potentialδφ and(b)parallel vector potential ‖δA of RSAE with n = 4,and(c)perturbed electrostatic potential and (d) parallel vector potential of ITG with n = 10.Red and yellow represent positive values, while blue and cyan represent negative values.
4.Conclusions
In summary,global GTC linear simulations using realistic DIIID tokamak geometry and plasma profiles with kinetic electrons,thermal ions, and fast ions find co-existence of unstable RSAE with low toroidal mode numbernand ITG instabilities with higher toroidal mode numbern.For intermediate toroidal modesn= [10, 12], RSAE and ITG eigenmodes overlap in the radial domain with similar growth rate but different real frequencies.The RSAE polarization is very close to ideal Alfvénic state,while the ITG polarization is closer to electrostatic but with significant magnetic perturbations.
Our simulations represent the first gyrokinetic simulation for the effects of compressible magnetic perturbations∣∣δBon the RSAE.In the current GTC simulations using realistic DIII-D magnetic geometry and plasma profiles, both RSAE and ITG growth rates decrease less than 5% when∣∣δBis neglected in the simulations.The effects of trapped electrons on the RSAE are negligible.Furthermore, ITG growth rates increase less than 7% when fast ions are not included in the simulations.Finally,GTC simulations find that the ITG in this DIII-D discharge become stable if electrons are adiabatic,i.e.by neglecting kinetic effects of trapped electrons.
The survey and understanding of the linear properties of these electromagnetic instabilities described in this paper provide a foundation for the next step of fully self-consistent gyrokinetic turbulence simulations treating both fast ions and thermal particles on the same footing to address the kinetic effects of thermal particles and the cross-scale coupling between microturbulence and mesoscale EP turbulence.
Acknowledgments
The authors would like to thank S Taimourzadeh and W W Heidbrink for providing the DIII-D equilibrium data (as published in [16]).We acknowledge technical support by the GTC team.This work was supported by the China National Magnetic Confinement Fusion Science Program (Grant No.2018YFE0304100), the US Department of Energy, Office of Science,Office of Advanced Scientific Computing Research and Office of Fusion Energy Sciences, and the Scientific Discovery through Advanced Computing(SciDAC)program under Award No.DE-SC0018270 (SciDAC ISEP Center), and the China Scholarship Council (Grant No.201806010067).This work used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory (DOE Contract No.DEAC05-00OR22725)and the National Energy Research Scientific Computing Center(DOE Contract No.DE-AC02-05CH11231).
 Plasma Science and Technology2021年1期
Plasma Science and Technology2021年1期
- Plasma Science and Technology的其它文章
- Effects of packing particles on the partial discharge behavior and the electrical characterization of oxygen PBRs
- Energy dissipation and power deposition of electromagnetic waves in the plasma sheath
- Modification of exposure conditions by the magnetic field configuration in helicon antenna-excited helium plasma
- Theoretical model and experimental investigation optically triggered hollowcathode discharge formation
- Electron population properties with different energies in a helicon plasma source
- Design and performance study of a gas-Cherenkov detector with an off-axis parabolic reflector for inertial confinement fusion experiments
