Finite type conditions on real hypersurfaces with one degenerate eigenvalue

Kohn’s finite type conditions in Care directly generalized by Bloom to higher dimensional spaces. Letting M be a real hypersurface of C, p is a point in M. For any integer s ∈[1,n],Bloom defined the regular s contact type a(M,p), the s commutator type t(M,p) and the s Levi-form type c(M,p). Bloom-Graham [3] and Bloom [4] proved a(M,p) =t(M,p) = c(M,p). In [5], Bloom conjectured that when M is pseudoconvex, then a(M,p)=t(M,p)=c(M,p).
Bloom also showed that a(M,p) = c(M,p) when M ?C. Recently, Huang-Yin [15]proved the Bloom conjecture for the case s = n-2; this leads to a complete solution of the conjecture for n = 3. One of the main results of the present paper is to solve this conjecture for hypersurfaces with at most one degenerate eigenvalue.
Theorem 1.1 Let M be a smooth pseudoconvex hypersurface in C, and let p be a point of M whose Levi form has at least n-1 positive eigenvalues. Then for each integer s ∈[1,n], we have a(M,p)=t(M,p)=c(M,p).
We would like to mention that Abdallah [1] has already proved a(M,p)=c(M,p) for the hypersurface in Theorem 1.1. However, pseudoconvexity is necessary in Theorem 1.1, as shown by Example 1.3, below.
Let L be a fixed tangent vector field of type (1,0) near the point p; here ρ is the defining function of M near p. D’Angelo[10] introduced the commutator type t(L,p)and the Levi form type c(L,p). Here t(L,p)is the least integer m,such that there exist L,··· ,L=L or L with〈[L,[L,··· ,[L,L]···],?ρ〉(p) /= 0. c(L,p) is the least integer m, such that there exist L,··· ,L=L or L with L···L〈[L,L],?ρ〉(p)/=0.
In [10], D’Angelo conjectured that when M is pseudoconvex, then for any tangent vector field L of type (1,0), we have t(L,p)=c(L,p).
D’Angelo proved the conjecture for when one of the two types is 4. Recently, Chen-Yin-Yuan [7] confirmed the conjecture for real hypersurfaces in C. The other main result of the paper is to prove this conjecture for hypersurfaces with at most one degenerate eigenvalue.
Theorem 1.2 Let M be a smooth pseudoconvex hypersurface in C, and let p be a point of M whose Levi form has at least n-1 positive eigenvalues. Then,for any(1,0)tangent vector field L, we have t(L,p)=c(L,p).
This theorem is stated without proof in[12]. It is worth pointing out that the pseudoconvex assumption is necessary in both Theorem 1.1 and Theorem 1.2, as shown by the following example:
Example 1.3 Let M be a real hypersurface in Cwith defining function
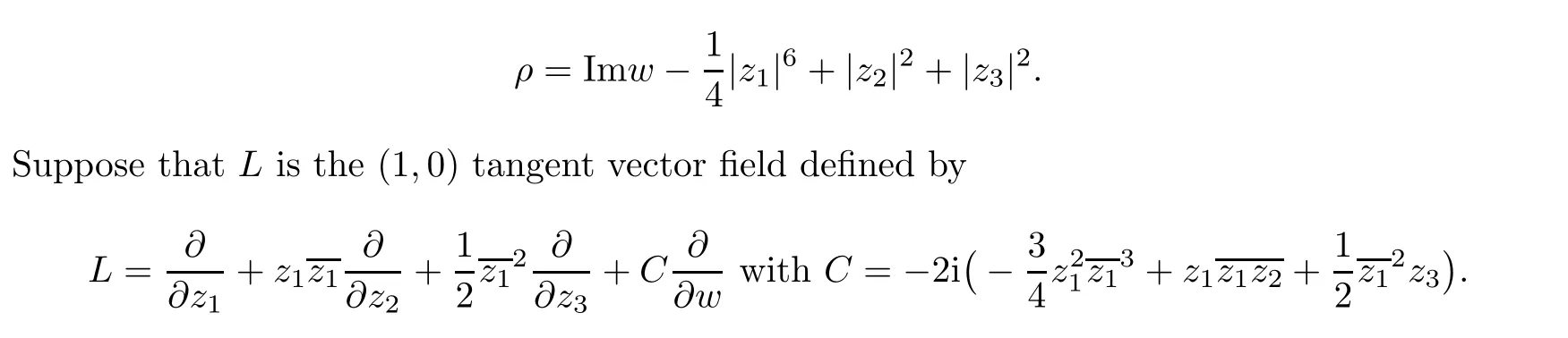
Then t(L,0)=∞, c(L,0)=6 and a(M,0)=6 <∞=c(M,0)=t(M,0).
2 A Weighted Homogeneous Version of the D’Angelo Conjecture
This section is devoted to proving a weighted homogeneous version of the D’Angelo Conjecture, which plays an important role in the proof of our main theorems.
Denote by (z,··· ,z,w) the coordinates in C. Let m be an integer and let m ≥2. In this section, we set the following weight system for z,··· ,z,w and their conjugates:
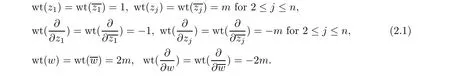
Let M be a weighted homogeneous hypersurface in C, whose defining function takes the following form near 0:

Here, for each α ∈[2,n], A(z,z) is a weighted homogeneous polynomial of weighted degree m-1, and A(z,z) is a weighted homogeneous polynomial of weighted degree 2m-1. Now we are in a position to state our homogeneous version of the D’Angelo conjecture.
Theorem 2.1 Let M and L be defined by (2.2) and (2.3), respectively. If M is pseudoconvex, then t(L,0)=c(L,0)=2m.
Proof From the Nagano theorem (see [2]), there exists an integral manifold N of the module generated by the real tangent vectors ReL, ImL and their commutators of all orders.Furthermore, by Freeman [14], N is weighted homogeneous with respect to the weight system given above.





Next we turn to the proof of c(L,0) = 2m. By a similar degree argument as to that in the proof of t(L,0) = 2m, we know that c(L,0) ≥2m. Suppose that c(L,0) >2m, and we will look for a contradiction. Again, let N be the integral manifold of the module generated by the real tangent vectors ReL, ImL and their commutators of all orders. Notice that for any L,··· ,L= L or L, L···L??ρ(L,L) is a weighted polynomial of degree 2m-k.Thus, if k /= 2m, it must be 0 when restricted to the origin. On the other hand, c(L,0)>2m implies that it is also 0 when k = 2m. Hence ??ρ(L,L)|= 0. This implies for any q ∈N,that Re(L),Im(L)∈TN. Here
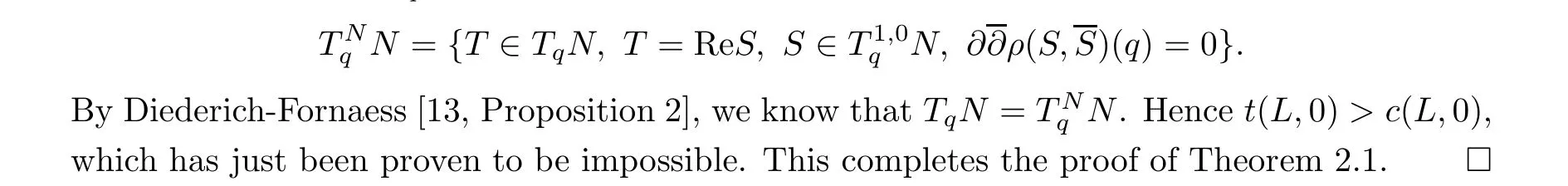
3 Proofs of the Main Theorems


By (3.6) with lreplaced by m, (3.8) implies that t(L,0)=c(L,0)=2m.
Hence we complete the proof of Theorem 1.2 in both cases.□
Proof of Theorem 1.1 Since the Levi form has at least n-2 positive eigenvalues, for any s ∈[2,n], we have that a(M,0)=t(M,0)=c(M,0)=2. Hence it suffices for us to consider the case s=1.
Suppose that a(M,0)=2m <∞. Then Theorem 1.2 shows that for any nondegenerate complex tangent vector field of type (1,0), t(L,0)≤2m and c(L,0)≤2m. Hence t(M,0)≤2m and c(M,0) ≤2m. On the other hand, by [5], we always have t(M,0) ≥a(M,0)and c(M,0)≥a(M,0). Thus t(M,0)=c(M,0)=a(M,0)=2m.□

Acknowledgements The authors would like to thank Professor Xiaojun Huang for helpful discussions.
 Acta Mathematica Scientia(English Series)2021年6期
Acta Mathematica Scientia(English Series)2021年6期
- Acta Mathematica Scientia(English Series)的其它文章
- REVISITING A NON-DEGENERACY PROPERTY FOR EXTREMAL MAPPINGS*
- THE BEREZIN TRANSFORM AND ITS APPLICATIONS*
- QUANTIZATION COMMUTES WITH REDUCTION,A SURVEY*
- Conformal restriction measures on loops surrounding an interior point
- Normal criteria for a family of holomorphic curves
- Multifractal analysis of the convergence exponent in continued fractions
