We use σ(f) to denote the order of f(z), λ(f) to denote the convergence exponent of zeros of f(z), and λ(f) to denote the convergence exponent of distinct zeros of f(z).

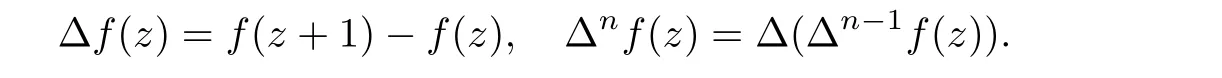
For n ∈N, we define Over the course of the last 15 years, many authors have paid great attention to complex difference equations and to the difference analogues of Nevanlinna’s theory, and have obtained many interesting results, including [2-6, 8, 10, 11, 15, 18, 19, 21, 23].

Ishizaki and Yanagihara [19] considered the growth of transcendental entire solutions of difference equations

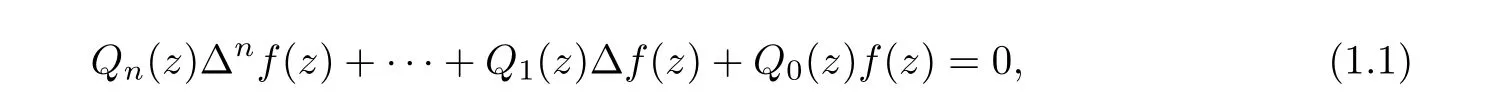
where Q,··· ,Qare polynomials, and obtained the following theorem:

Theorem A Let f(z) be a transcendental entire solution of (1.1), and let its order χ ＜1/2. Then

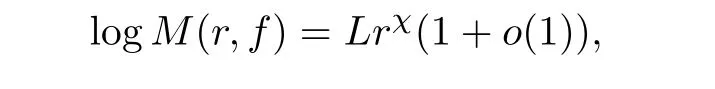
where a rational number χ is the slope of a Newton polygon for the equation (1.1), and L ＞0 is a constant. In particular, we have that χ ＞0.

Note that the equation (1.1) can be rewritten as

Example 1.1 (see [19]) Suppose that f(z) is a transcendental entire solution of the difference equation

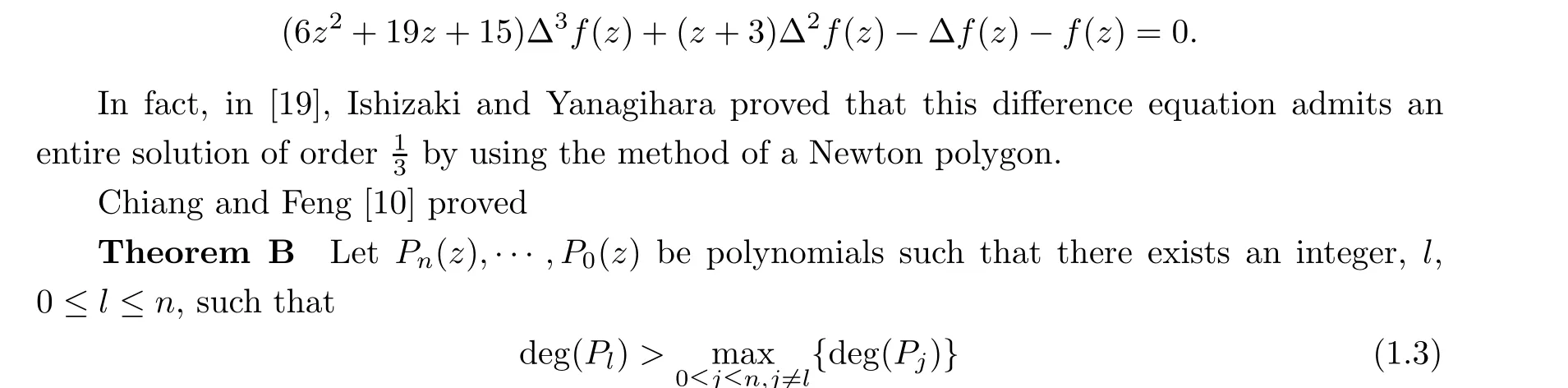
holds. Supposing that f(z) is a meromorphic solution of (1.2), we then have that σ(f)≥1.Chen weakened the condition (1.3) of Theorem B and obtained

Theorem C (see [4,5]) Let F(z),P(z),··· ,P(z)be polynomials such that FPP/≡0 and

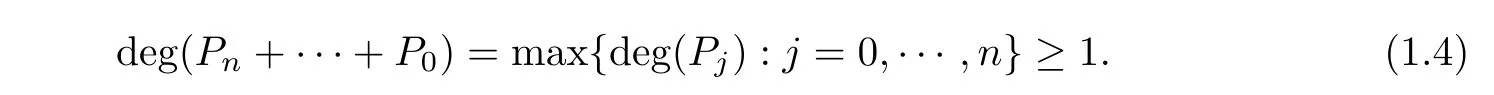
Then every finite order transcendental meromorphic solution f(z) of

satisfies σ(f)≥1 and λ(f)=σ(f).

Theorem D (see [4, 5]) Let P(z),··· ,P(z) be polynomials such that PP/≡0 and(1.4) is satisfied. Then every finite order transcendental meromorphic solution f(z)(/≡0) of equation (1.2) satisfies σ(f)≥1, and f(z) assumes every non-zero value a ∈C infinitely often and λ(f -a)=σ(f).

Chen considered difference equations with constant coefficients,and obtained the following two theorems:

Theorem E (see [4]) Let C,··· , Cbe constants such that CC/= 0 and such that they satisfy

Then every finite order transcendental meromorphic solution f(z)(/≡0) of the equation

satisfies σ(f)≥1,f(z)assumes every nonzero value a ∈C infinitely often,and λ(f-a)=σ(f).

Theorem F Let C,··· , Cbe constants and let F(z) be a polynomial such that FCC/≡0 and (1.6) is satisfied. Then every finite order transcendental meromorphic solution f(z) of the equation

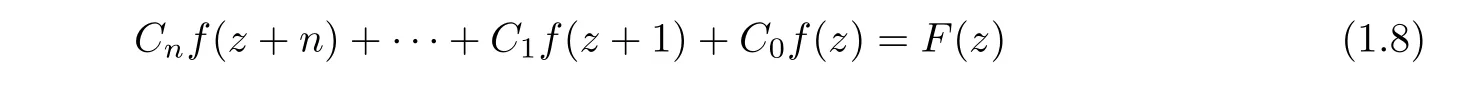
satisfies that λ(f)=σ(f)≥1.

Question 1.1 Can the condition (1.6) be deleted from Theorems E and F?

In this paper, we answer this question in the affirmative and delete condition (1.6) from Theorems E and F, and obtain the following theorems:

Theorem 1.1 Let C,··· , Cbe constants such that CC/=0. Then every finite order transcendental meromorphic solution f(z)(/≡0) of the equation (1.7) satisfies that σ(f)≥1.

Theorem 1.2 Let C,··· , Cbe constants, and let F(z) be a polynomial such that FCC/≡0. Then every finite order transcendental meromorphic solution f(z)of the equation(1.8) satisfies that λ(f)=σ(f)≥1.

Remark 1.1 In Theorems 1.1 and 1.2, we have deleted condition (1.6) of Theorems E and F.

In Theorem 1.1, we cannot give the result that every finite order transcendental meromorphic solution f(z) of (1.7) assumes every nonzero value a ∈C infinitely often and that λ(f -a)=σ(f).

In Theorem 1.2, we obtain the same results as for Theorem F.

Remark 1.2 By Theorems 1.1 and 1.2, we see that in Theorems C and D, the condition(1.4) can be weakened as

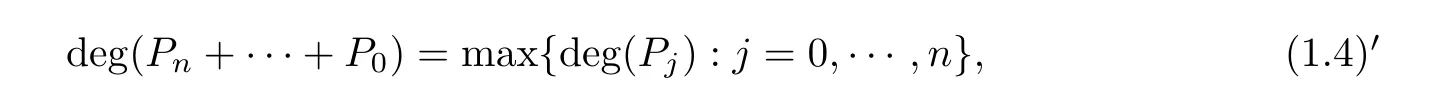
where “≥1” of (1.4) is deleted. Thus, we can obtain the following corollaries:

Corollary 1.1 Let F(z),P(z),··· ,P(z)be polynomials such that FPP/≡0 and such that they satisfy (1.4). Then every finite order transcendental meromorphic solution f(z) of(1.5) satisfies that σ(f)≥1 and λ(f)=σ(f).

Corollary 1.2 Let P(z),··· ,P(z) be polynomials such that PP/≡0 and such that they satisfy (1.4). Then every finite order transcendental meromorphic solution f(z)(/≡0) of(1.2) satisfies that σ(f)≥1.

Since 1982,many authors have studied the growth of solutions of linear differential equations and obtained many good results, see [7, 9, 12, 14].

Now, we consider the growth of solutions of homogeneous and non-homogeneous linear differential equations with constant coefficients, and obtain the following results:

Theorem 1.3 Let C,··· , Cbe constants such that CC/=0. Then every meromorphic solution f(z)(/≡0) of the homogeneous differential equation

Remark 1.3 From Theorems 1.1 and 1.3, we see that for homogeneous equations (1.7)or (1.10), we can only obtain that σ(f)≥1 or σ(f)=1.

From Theorems 1.2 and 1.4,we see that for non-homogeneous equations(1.8)or(1.11),we can obtain that λ(f)=σ(f)≥1 or λ(f)=σ(f)=1.

Remark 1.4 From Theorem 1.3,we see that homogeneous equation(1.10)does not have a polynomial solution. From Theorem 1.4, we see that non-homogeneous equation (1.11) may have a polynomial solution.

Example 1.4 The differential equation

has solutions f(z)=cos z and σ(f)=1.

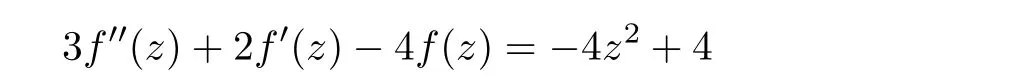
Example 1.5 The differential equation has a polynomial solution f(z)=z+z+1.

2 The Asymptotic Method

Theorem G (see [17(p.30), 20]; the Wiman-Valiron Theory) Suppose that f is a transcendental entire function, and that for any given 0 ＜δ ＜1/8, there exists a set H of finite logarithmic measure such that

and the corresponding homogeneous linear differential equation

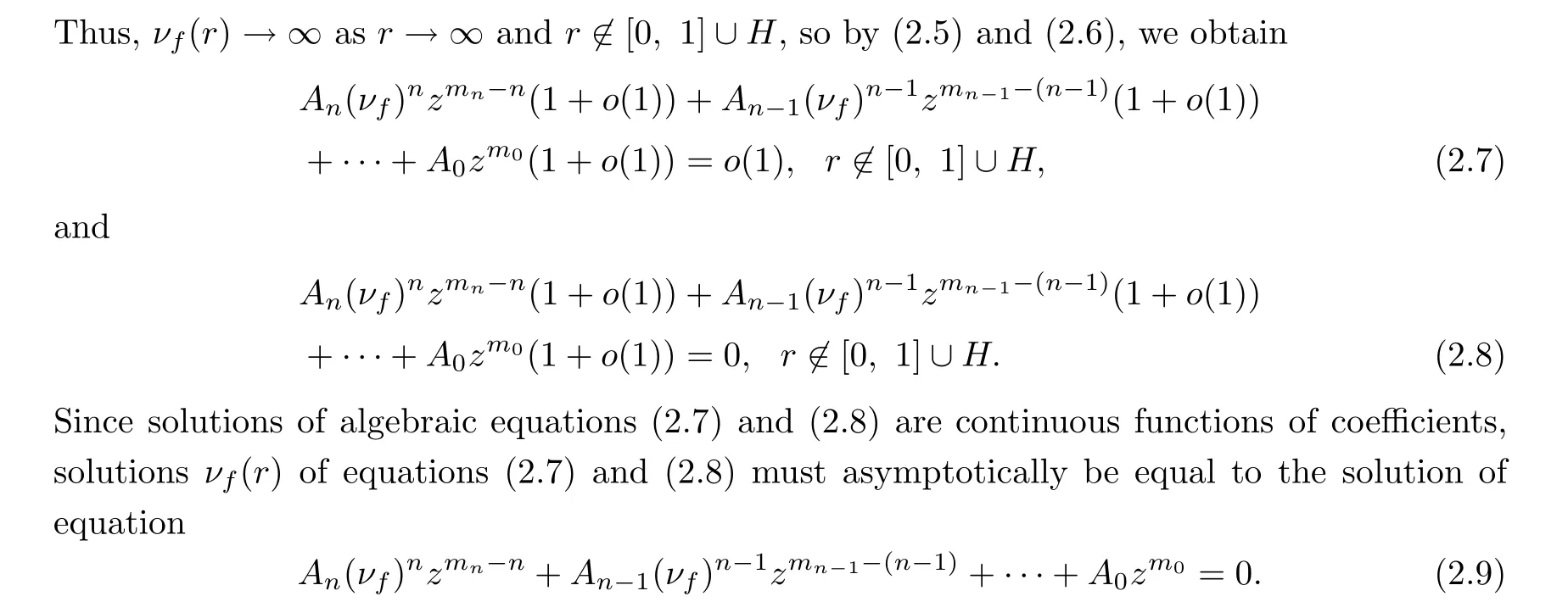
Since the solution νof (2.9) is an algebraic function of z, setting the principal part of νas a(ρ)z(a, ρ are nonzero real numbers) in the neighborhood of z =∞, we get that,

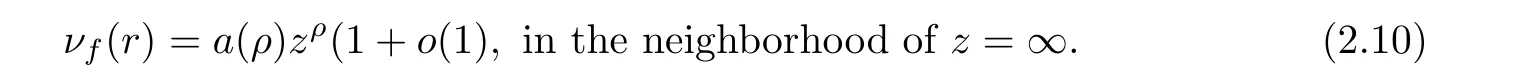
By (2.9) and (2.10), it is easy to see that the degrees of all of the terms of the left of (2.9) are

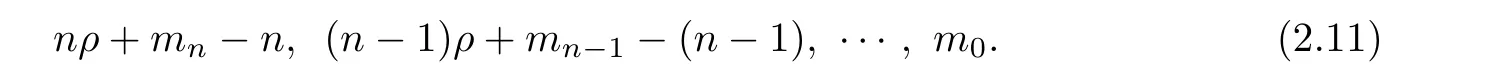
Since ν(r) is the solution of (2.9), we see that in (2.11), at least, there are two terms that are both the largest numbers and equal, and that the sum of coefficients of their corresponding terms in (2.9) is zero. Hence, ρ satisfies that we have i and j such that

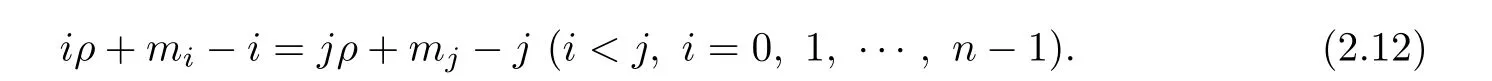
Thus, we see that ρ is a rational number, and we have at most n such rational numbers that are not less than 1/n.

3 Proofs of Theorems 1.1 and 1.2

We need the following lemmas to prove Theorems 1.1 and 1.2:

Lemma 3.1 (see [2, 4]) Let n ∈N, and let f be a transcendental meromorphic function of an order less than 1. Then there exists an ε-set Esuch that

Since Eare ε-set, we see that a set His of finite logarithmic measure. By (3.1)and (3.2), we obtain that By (3.7) and (3.8), we see that (3.6) is a contradiction.

Hence, every finite order transcendental meromorphic solution f(z)(/≡0) of the equation(1.7) satisfies that σ(f)≥1.□

Proof of Theorem 1.2 Using the same method as in the proof of Theorem 1.1,we can prove that every finite order transcendental meromorphic solution f(z) of the equation (1.8)satisfies σ(f)≥1.

Now, we prove that every finite order transcendental meromorphic solution f(z) of the equation (1.8) satisfies λ(f)=σ(f).

By (1.8), we set

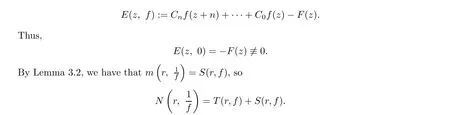
Hence, λ(f)=σ(f).□

4 Proofs of Theorems 1.3 and 1.4

Proof of Theorem 1.3 It is well known that all meromorphic solutions of equations(1.10) are entire functions.

Suppose that f(z) is a solution of (1.10).

First, we prove that f(z) cannot be a polynomial. If f(z) is a nonzero constant, then f(z) = ··· = f(z) = 0, and this is not possible. If f(z) is a polynomial with deg f(z) ≥1,then deg f(z)＜deg f(z) (j =1,··· ,n) which is also not possible.

Now, we suppose that f(z) is a transcendental entire function with σ(f)=σ.

By the Wiman-Valiron theory,we see that there exists a set Hof finite logarithmic measure such that (3.4) holds, where |f(z)| = M(r,f),|z| = r /∈[0,1]∪H∪H, ν(r,f) is the central index of f(z). By (3.4) and (1.10), we obtain

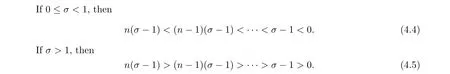
Thus, by (4.4) and (4.5), we see that (4.1) is a contradiction.

Hence, by (4.4) and (4.5), we see that σ = 1, that is, every solution f(z)(/≡0) of the equation (1.10) satisfies σ(f)=1.

Theorem 1.3 is thus proved.□

Proof of Theorem 1.4

We need the following lemma:

Lemma 4.1 (see [13, pp. 168]) Suppose that a, a, ··· , a, F /≡0 are entire functions, that f satisfies the differential equation

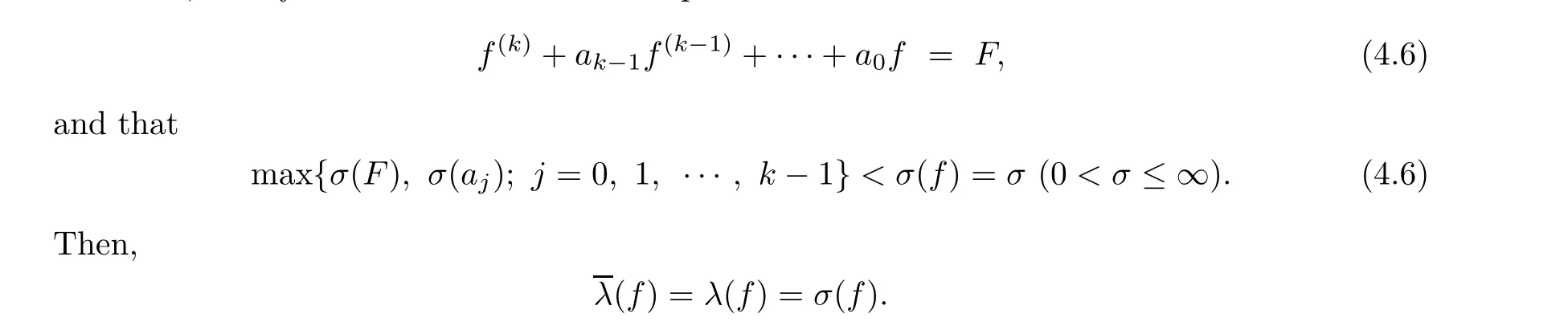
Proof of Theorem 1.4 Using the same method as in the proof of Theorem 1.3, we see that all meromorphic solutions of equations (1.11) are entire functions, and if f(z) is a transcendental entire solution of (1.11), then σ(f)=1.

Since C(j =0,··· ,n)are constants,F(z)/≡0 is a polynomial,and thus C,F(z)and f(z)satisfy condition (4.6) of Lemma 4.1. By Lemma 4.1, we obtain that λ(f)=λ(f)=σ(f)=1.

Theorem 1.4 is thus proved.□