Probing time delay of strong-field resonant above-threshold ionization*
Shengliang Xu(徐勝亮), Qingbin Zhang(張慶斌),?, Cheng Ran(冉成),Xiang Huang(黃湘), Wei Cao(曹偉), and Peixiang Lu(陸培祥),2
1School of Physics and Wuhan National Laboratory for Optoelectronics,Huazhong University of Science and Technology,Wuhan 430074,China
2Hubei Key Laboratory of Optical Information and Pattern Recognition,Wuhan Institute of Technology,Wuhan 430205,China
Keywords: above threshold ionization,resonant ionization delay,transition selection rule
1. Introduction
Ionization stands out as one of the most fundamental processes in light-matter interaction,[1,2]since it triggers the subsequent electron dynamic in the continuum, and therefore affects many important processes such as photoelectron holography,[3,4]high-harmonic generation,[5,6]and nonsequential double ionization.[7–10]For this reason, resolving the ionization process in its inherent ultrafast time scale becomes key for understanding and steering free-electron dynamics as well as reactions.The advanced attosecond metrologies, for example, reconstruction of attosecond beating by interference of two-photon transitions (RABBITT) and attosecond streaking (AS), have made it possible to measure the ionization process in attosecond resolution. With these technologies, a noticeable delay in photoemission from the ground state to continuum for atoms, molecules, and solids was observed.[11–15]
As compared to releasing the photoelectron directly into the continuum, the electron may also be first promoted to laser dressed intermediate state via resonant excitation, and then released into the continuous state in the laser field.[16]The involution of intermediate states introduces an additional phase during the transition, which is believed to relate to the predicted extra delay.[9,17,18]In fact, the experimentally measured ionization delay contains contributions from both the intrinsic ionization delay and the extracted time delay induced by the coupling of the long-range Coulomb and the laser field.[20,21]The former one is also known as quantum-mechanical Eisenbud–Wigner–Smith (EWS) delay,which provides unique insight into the structural and transport dynamics in systems.[22–24]The latter one is assumed physically unimportant but cannot be excluded in the present of a strong laser field. To disentangle the two contributions and resolve the intrinsic ionization dynamics, experimentally, the noble gas atoms have been adopted as a benchmark to calibrate the measured delays in more complicated systems.[25]Alternatively, a self-referenced measurement is implemented for different resonant channels, and thereby highlighting the relative ionization time delay between different pathways. A recent experiment observed the Freeman resonance delay between ionization through 4f and 5p Rydberg states of argon is 140±40 as.[19]
So far, most studies related to the measurement of Freeman resonant ionization dynamics rely on attosecond pumpprobe method with linearly polarized light.[19,26]While the angular streaking method is a relatively simple method,which provides the attosecond time resolution without the explicit need of attosecond pulses.[27,28]This approach defines a good mapping relationship between instant of ionization and final angle of the momentum vector in a near circularly polarized laser field,offering a time resolution of a few attoseconds.[29]Using this method, considerable research efforts have been devoted to time measurement of the release of electron directly from the ground state to the continuous state or verify the nonadiabaticity in a strong field,with Keldysh parameters spans from 0.1 up to 4.[30]In this paper,by employing a near circularly polarized laser field,angular resolved photoelectron momentum distribution (PMD) is measured, allowing us to look into the ultrafast ionization dynamics. More importantly,the use of the near circularly polarized laser field provides us a unique opportunity to select the specific intermediate states,for example, 4f and 5f Rydberg states in our work. Thus it will facilitate refining experimental observations and deepen the understanding of the role of resonant transition during ATI.
2. Experimental setup
The laser pulses used for the implementation of the experiment are generated from a Ti:sapphire laser system,and then they are frequency doubled to 410 nm(=3.03 eV)with a 300 μm-thick β-barium-borate crystal. The linearly polarized laser pulse is converted into right elliptically polarized(REP)light by passing through a λ/4 waveplate,with the ellipticity ε =0.7. The laser pulse used in our experiment is characterized by the home-made cross-correlation frequency-resolved optical gating (XFROG) technique and the pulse duration is 115 fs. The laser is focused onto the supersonic Xe gas beam by a plano-convex lens(f =30 cm)to measure the projected PMD with velocity map imaging(VMI)as shown in Fig.1(b).To obtain the three-dimensional PMD by applying the tomographic reconstruction,the acquisition of the projected PMDs under a number of angles is required.[31–33]This multiangle measurement is achieved by rotating the polarization of laser with a λ/2 waveplate mounted on a motorized rotation stage at a step size of 0.1?.

Fig.1. (a)The interpretation of nonadiabatic tunneling as absorption of photons followed by tunneling with 4f and 5f intermediate states. (b)Schematic view of the experimental setup.
3. Results and discussion
The Keldysh parameter γ (nonadiabatic factor) is calculated to be 2.78 with our laser parameters. Here, we generalize the static picture of tunneling into the nonadiabatic regime.To make the ionization process clearer and more intuitive,the interpretation of nonadiabatic tunneling as absorption of photons followed by tunneling with 4f and 5f intermediate states is shown in Fig. 1(a). We first discuss the selection of the specific intermediate states using REP laser field. As we all know,when electron’s spin is parallel to its orbital angular momentum,removing a valence electron from Xe could yield the ground state of the ion(ionization potential Ip=12.13 eV with total angular momentum J =3/2), while the emission of an electron with opposite spin(j=1/2)leads to the first excited state of the ion(total angular momentum J=1/2).[34]The two combs of ATI peaks belonging to two ionic states(J=3/2 and J=1/2)with an energy difference of 1.31 eV do not overlap in our photoelectron energy spectrum.[35]Since the measured energy difference of two ATI peaks via 4f and 5f intermediate states belonging to ionic ground state is only 0.37 eV, which is much less than 1.31 eV, we therefore only concentrate on the PMD belonging to the ionic ground state. Corresponding to the ionic ground state, there exists three degenerate p orbitals of valance electron for Xe, the p+orbital (m=+1),p- orbital (m=-1), and p0orbital (m=0). The magnetic quantum number m=-1(m=+1)refers to the projection of the angular momentum in the quantization axis (z axis, light propagation direction)is-1(+1),which means that the electron ring currents in polarization plane (xy plane) is counterrotating (co-rotating) in the sense as the REP field. In practice, the ionization of p0orbital is strongly suppressed and therefore neglected.[36]To resonantly ionize Xe,four 410-nm photons are required to first promote valance electron from the ground state to intermediate state,and then the electron is liberated into continuum nonadiabatically in laser field. For linearly polarized light,this four-photon excitation is allowed between states that are the same in the parity,therefore,|p,±1〉,|f,±1〉, |h,±1〉, |f,±3〉, |h,±3〉 and |h,±5〉 states can be populated during the process of ionization. While the selection rule is more strict for circularly polarized light, that is,the absorption of one photon of circularly polarized light will change the magnetic quantum number either by +1 or -1 monotonously. For the REP field used in our experiment,the absorption of one photon for resonant ionization is assumed to increase the magnetic quantum number by Δm=+1. Therefore, the number of intermediate states plays in the role that can be cut down and the analysis would be simple.In this case,the accessible intermediate states become sensitive to the helicity of initial p orbital. The possible excitation pathways are|p,-1〉→|f,+3〉, |p,-1〉→|h,+3〉 and |p,+1〉→|h,+5〉.Because of the dynamic Stark effect in the presence of strong laser field, the bound intermediate states |h,+3〉, |h,+5〉 and|f,+3〉of Xe all shift upward along with the ionization potential by approximately Up=e2I/(2cmε0ω2) with the electric permittivity of free space ε0, the speed of light c, the charge e,mass m of the electron,the laser intensity I and angular frequency ω. Compared to the h series states,the f series states with originally lower energy need to be lifted more to match the energy of the four photons. Therefore,the resonant ionization of f series states requires higher laser intensity,resulting in a much higher ionization rate at resonance due to the highly nonlinear ionization rate as a function of intensity. Among all the f series Rydberg states, achieving resonance with the lowest-lying 4f and 5f states requires the highest laser intensity which leads to highest yield.Meanwhile the energy difference of these two states is largest.Thus the resonant ionization pathways via 5f(channel 1)and 4f(channel 2)states shown in Fig.1(a)are easiest to identify in the measured PMD.
Figure 2(a)shows the measured PMD in REP laser field at 5.5×1013W/cm2.We can clearly see that the PMD exhibits an obvious double-ring structure,and energy separation of the double rings is approximately 0.32 eV, which matches well with the energy separation of 4f and 5f energy levels available in the National Institute of Standards and Technology(NIST).[37]The double-ring ATI structure in PMD originated from resonant excitation via the intermediate 4f and 5f states is also supported by the fact that these two ATI ring energies are independent of intensity,[38]as shown in Figs.2(b)and 3.In earlier studies,two scenarios were suggested for explaining the intensity-independent rings in resonant ATI.First,one[39]assumes that electron ionizes from an excited state to a continuous state before the intensity has considerably changed. The resonance condition can be fulfilled somewhere in the laser focus when the peak intensity is higher than the resonant value.The second scenario[40]suggests that a high-lying Rydberg state can be shifted upwards almost as much as the continuum level and give rise to intensity-independent peak positions. To quantify the observed two resonant ATI rings, we further depict the angle-and energy-resolved photoelectron spectrum in Fig.2(c). We can clearly find considerable angular offset difference for two rings with close energies. This offset angle is expected to reflect the ionization time difference between the two ionization channels, according to the mapping relationship Δθ =ωΔt in angular streaking. In angular streaking,the electron is born necessarily at the peak of electric field,in order to assign unambiguously the most probable photoemission offset angle to the moment when the laser field reaches its peak. To verify this,we experimentally compared the PMD of a circularly polarized laser field with that of a near-circularly polarized laser field. For every cyclic structure,there are two peaks which are almost centrosymmetric with respect to the zero momentum in the PMD in near-circularly polarized laser field (Fig. 2(a)), while the PMD is isotropous in circularly polarized laser field (not shown). This result evidently suggests that the two-peak angular distribution is a consequence of the major axis of the polarization ellipse. It must also be mentioned that the momentum of the most probable electrons,which is determined by the vector potential of the light field along major axis of the polarization ellipse,deviates from the minor axis of the polarization ellipse. This deviation is believed to be due to the Coulomb interaction and the nonadiabatic effect during the ionization process.[30]In the application of timing absolute ionization time delay,therefore it is necessary to precisely calibrate the deviation angle with respect to the minor axis of the polarization ellipse, in order to determine time zero.[41]However,the calibration is nontrivial. Until recently, several schemes rely on two-color circularly polarized laser field,which was proposed for achieving an easier and better calibration.[42,43]Here,we extract considerable offset angle difference between two resonant ionization channels with very close energy. Since we measure the difference, we do not need to calibrate the deflection angle for each ionization channel. They are automatically eliminated in the process of subtracting for obtaining relative ionization time, as long as the Coulomb attractions are similar for the two ionization pathways,which has been proved in the following paragraphs.When involving the excited intermediate states, the electron motions under the barrier can be much more complex. The 45.6 as time difference,reading out from the 12?offset angle difference,is strong experimental evidence of how intermediate states affect the ATI process.

Fig.2. (a)Measured PMD of the ATI belonging to the 2P3/2 ionic state in polarization plane (x–y plane) with |Pz|<0.92 a.u. The offset angle difference Δθ of two ionization channels (4f and 5f) is 12?. The blue curve represents the elliptically polarized light field. (b)The measured photoelectron energy distributions with the laser intensities from 4.5×1013 W/cm2 to 5.5×1013 W/cm2. The two resonant ATI peaks are labeled by two grey dotted lines.(c)Measured photoelectron energy distribution with the emission angle from 5?to 355?.The laser intensity is 5.5×1013 W/cm2 for both(a)and(c).
Next,we prove that the Coulomb interactions for two ionization channels are similar. As we know that the Coulomb interaction between the parent ion and electron is very sensitive to the electron’s kinetic energy. Usually, the slower (faster)electrons will be more strongly (more weakly) deflected. In the earlier studies, it has been demonstrated that intensity is a useful knob to shift the position of ATI peak in the energy domain due to the pondermotive energy shift.[44,45]Therefore,the Coulomb effect can be compared between ATI peaks with very close energies by changing laser intensity slightly. We first show how the ATI peaks are shifted in the energy domain by varying the laser intensity from 2.6×1013W/cm2to 8.4×1013W/cm2in Fig.3. The results are obtained by solving the time-dependent Schr¨odinger equation for Xe atom as given by


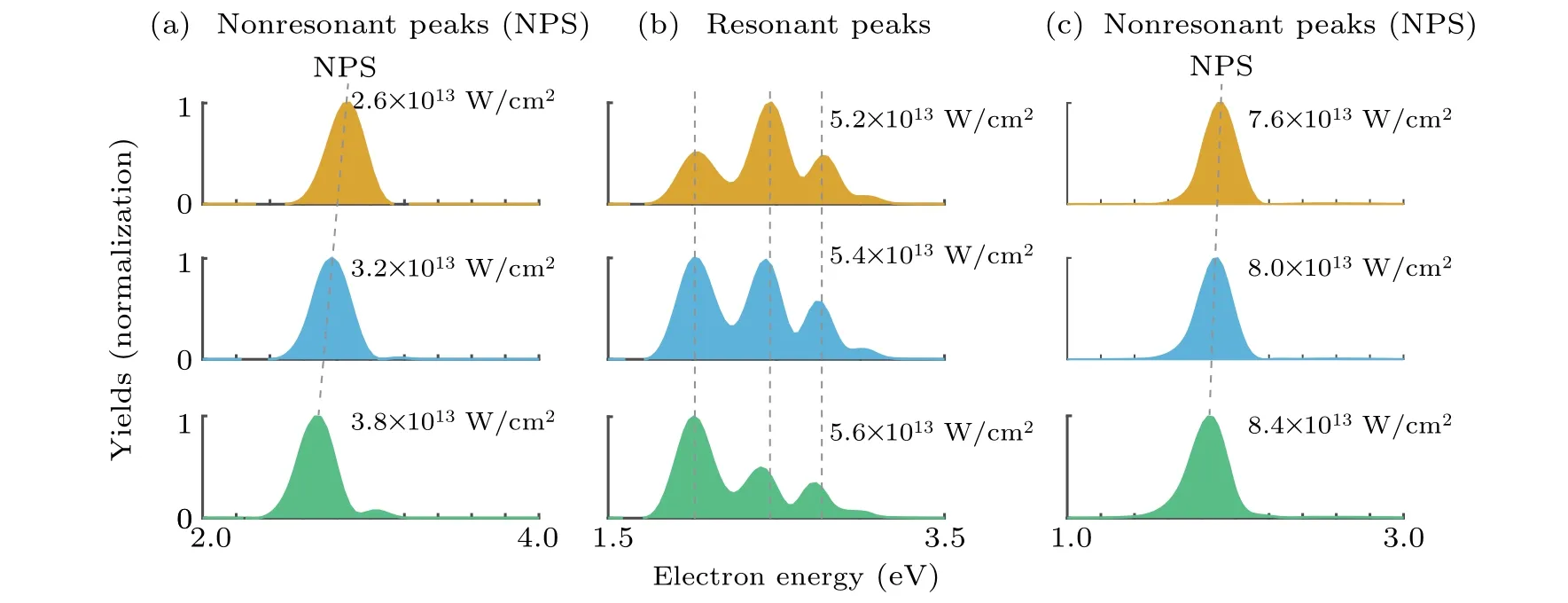
Fig.3. (a)–(c)The simulated photoelectron energy distributions with the laser intensities from 2.6×1013 W/cm2 to 8.4×1013 W/cm2. The yield is normalized for each laser intensity.

Table 1. Energies(eV)of the first 6 lowest-lying eigenstates for m=0,±1,±2,±3,±4.
We then compare the influence of the Coulomb deflection for the resonant ionization with different laser intensities. When laser intensity changes from 4.5×1013W/cm2to 5.5×1013W/cm2, the experimentally measured offset angle for resonant ionization via 4f (5f) intermediate state is fixed at 38?(50?) as shown in Fig. 4(a). Here, the offset angle θ is calculated by θ =θstreak-90?. This finding suggests that for each resonant ionization channel, Coulomb effects at different laser intensities are similar, where photoelectrons have the same final energy. The numerical calculation also supports the result that the offset angle of most probable emission photoelectron wave packet of resonant ionization via two intermediate states(m=3)is independent of laser intensity.The simulated photoelectron angular distributions with the laser intensities from 4.8×1013W/cm2to 5.4×1013W/cm2are shown in Fig.4(b). The offset angles of most probable emission photoelectron wave packets via two intermediate states are 64?and 78?with a fixed angle difference of 14?, which is slightly larger than the experimental result. The small deviation from the experiment may be caused by the reduced dimensional model which overestimates the Coulomb effect slightly and ignored intensity averaging in focusing volume.
We finally turn to estimate how much offset angle difference will be introduced by the Coulomb deflection for the two resonant ionization channels mentioned above. For these two resonant ionization channels, the offset angle difference is contributed by both resonant ionization delay and different Coulomb deflections. If the difference on Coulomb deflection is small enough, then the difference on the offset angle can be attributed to the ionization time delay for the two resonant channels. To extract the Coulomb deflection difference, we compare the offset angle between two nonresonant ATI peaks,the energy of which is lower and higher than the resonant ATI peaks. In principle, the Coulomb deflection induced difference on the offset angle should be larger for these two selected nonresonant ATI peaks because they have larger energy difference compared to the two resonant ATI peaks. In Fig. 5, we show the energy and angle of the ATI peak for various laser intensities. With the increase of laser intensity, the ATI peak shifts towards lower energy and the corresponding offset angle becomes larger. The two nonresonant ATI peaks whose offset angle will be compared are chosen at the two boundaries of the resonant region, which are determined from Fig. 3. The energy difference between the two nonresonant ATI peaks is 0.75 eV and the time delay (offset angle difference) between them is 11.4 as(3?)as indicated by the black dashed lines in Fig. 5. Thus the offset angle difference induced by Coulomb deflection for the two resonant ATI peaks with a smaller energy difference will not exceed this value. Recalling the fact that the offset angle difference between the resonant 4f and 5f ATI peaks is greater than 10?both in experiment and numerical simulation, we can conclude that this offset angle difference is mainly contributed by the ionization delay between the two resonant ionization channels.

Fig. 4. (a) The measured photoelectron angular distributions with the laser intensities of 4.5×1013 W/cm2, 5.0×1013 W/cm2 and 5.5×1013 W/cm2.The offset angle difference Δθ of two ionization channels is 12?for three laser intensities.The photoelectron angular distributions via 4f and 5f intermediate states are labeled by the green dashed line and red dot-dashed line. (b) The simulated photoelectron angular distributions with the laser intensities of 4.8×1013 W/cm2, 5.0×1013 W/cm2, 5.2×1013 W/cm2 and 5.4×1013 W/cm2. The offset angle difference Δθ of the two ionization channels is 14?for four laser intensities.

Fig.5. The simulated final energy and offset angle of the ATI peak for initial|p,m=-1〉state electrons are shown in this part.The laser intensities are from 2.8×1013 W/cm2 to 8.4×1013 W/cm2. The predicted position of resonant region is labeled by a green rectangle. The minimum value of the longitudinal axis for the offset angle is set to 0. The offset angle difference for the two boundaries of the resonant region is labeled by black dashed lines.
4. Conclusion
In summary, we have experimentally observed a 45.6 as difference of strong-field ionization time via the field-dressed 4f and 5f states of Xe atoms. The REP field allows us to unambiguously select specific resonant intermediate states in the self-reference measurement. The selected states differ only in principal quantum number while have the same magnetic quantum number, which is in favor of highlighting the role of the radial part of electron orbital during resonant excitation. Our findings advance the understanding of sub-cycle photoionization dynamics,and shed light on the manipulation of ultrafast electron dynamics in laser-matter interactions.
- Chinese Physics B的其它文章
- Two-dimensional finite element mesh generation algorithm for electromagnetic field calculation*
- Stable water droplets on composite structures formed by embedded water into fully hydroxylated β-cristobalite silica*
- Surface active agents stabilize nanodroplets and enhance haze formation*
- Synchronization mechanism of clapping rhythms in mutual interacting individuals*
- Theoretical study of the hyperfine interaction constants,Land′e g-factors,and electric quadrupole moments for the low-lying states of the 61Niq+(q=11,12,14,and 15)ions*
- Ultrafast photoionization of ions and molecules by orthogonally polarized intense laser pulses: Effects of the time delay*