安徽省滁州中學(239000) 劉穩(wěn)俠

題目(2020年蘇錫常鎮(zhèn)四市高三調(diào)研試題)如圖, 在ΔABC中,AB= 4,D是AB的中點,E在邊AC上,AE= 2EC,CD與BE交于點O, 若OB=則ΔABC面積的最大值為?

以下我們分兩步給出多種解法,供大家學習與借鑒.

解題思路第一步:確定點O位置;第二步:計算面積最大值.首先我們給出第一步的6 種解法.

解法1(向量法:三點共線)設=又E,O,B三點共線,所以所以解得故即點O是CD的中點,由題所以OB=即

解法2(向量法:定比分點)

引理在ΔABC中,與BE交于點O, 連接AO, 則

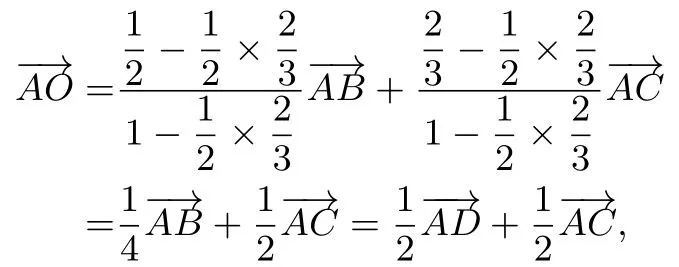
故點O是CD的中點, 由題OB=所以OB=即

解法3(幾何法:構造平行線)過點D作DF平行于BE交于點F,如圖1.因為D是AB的中點,則點F是AE的中點,又因為DF平行于OE,所以點O是CD的中點,由題OB=所以OB=即

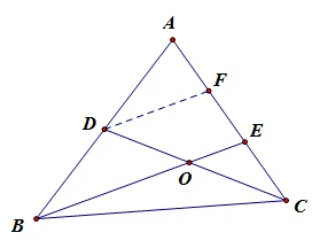
圖1

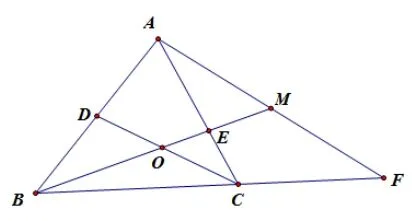
圖2

解法4(幾何法:構造三角形重心)如圖2, 延長BC,使CF=BC, 連接AF, 延長BE交AF與點M, 則點E是ΔABF的重心,因為CD平行于AF,且AM=MF,所以OC=OD,由題OB=所以OB=即

解法5(杠桿原理, 即塞瓦圖形標數(shù)法)記A,B,C,D處質(zhì)量分別為mA,mB,mC,mD, 設在A點處放置一個質(zhì)量為1 的質(zhì)點, 把AC看成杠桿,E點為支點, 由杠桿平衡條件, 則同理可得mB=mA= 1, 又mD=mA+mB= 2, 所以= 1, 即OC=OD, 由題OB=所以OB=,即

解法6(代數(shù)法)以D為坐標原點, 建立如圖3 所示平面直角坐標系.則A(2,0),B(-2,0), 設C(x0,y0), 則

直線CD方程為

直線BE方程為

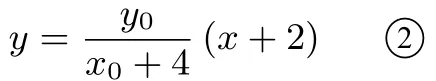
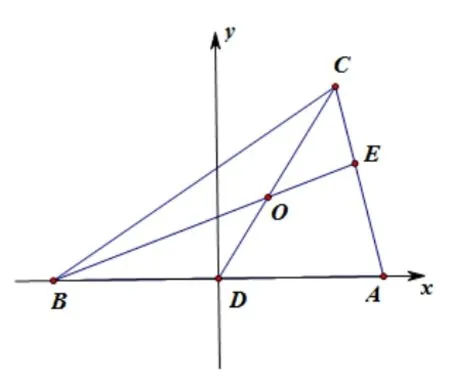
圖3

以下給出第二步的5 種解法.

解法1(建系,構造阿氏圓方程)以D為坐標原點,BA為x軸,建立如圖3 所示平面直角坐標系,則A(2,0),B(-2,0),設O(x,y), 由OB=可得(x+2)2+y2=2(x2+y2), 化簡得(x-2)2+y2= 8(y ?=0), 即O點在以(2,0)為圓心,為半徑的圓周上(去掉與x軸相交的兩點),所以SΔABC= 2SΔAOB≤即ΔABC面積的最大值為

解法2(用阿氏圓性質(zhì)求最值)阿氏圓的性質(zhì):設A,B是平面內(nèi)的兩個定點,平面內(nèi)動點C到點A的距離和點B的距離的比值λ(λ ＞0 且λ ?= 1),則點C的軌跡是圓,且圓心在AB上,半徑

解法3(代數(shù)法:設C點坐標)以D為坐標原點,BA為x軸,建立如圖3 所示平面直角坐標系,則A(2,0),B(-2,0),設C(x,y),則由OB=可得化簡得(x-4)2+y2=32(y ?=0),當x= 4 時,|y|max=所以ΔABC面積的最大值為SΔABC==×4×

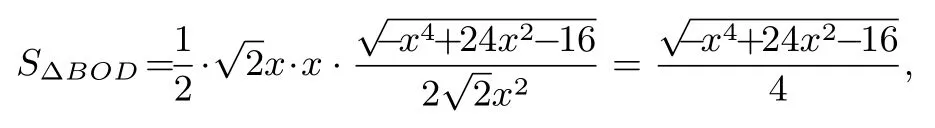
解法4( 函數(shù)最值)設|OC|=|OD|=x, 則|OB|=記∠BOD=θ, 由余弦定理得,所以, sin2θ= 1-sinθ=其中-x4+ 24x2-16 =-(x2-12)2+ 128 ≤ 128,所以(SΔBOD)max=(SΔABC)max=4(SΔBOD)max=即ΔABC面積的最大值為

解法5(巧用向量)

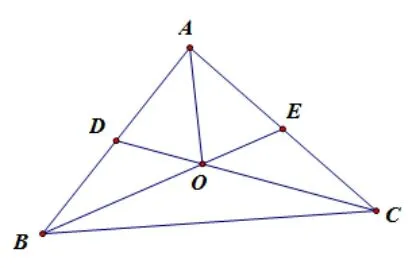
圖4

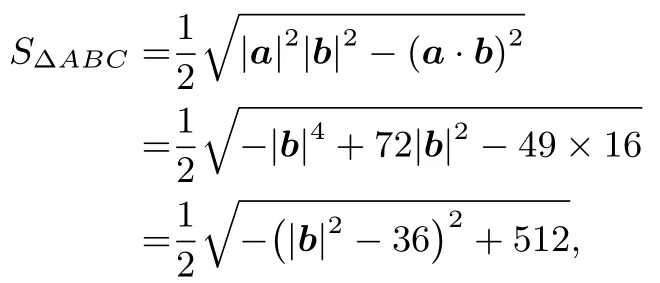
所以當|b|=6 時,ΔABC面積取最大值為