ASYMPTOTIC STABILITY OF A VISCOUS CONTACT WAVE FOR THE NE-DIMSIAL CPBL VK QU G X*
Lishuang PENG (彭利雙)
College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China
E-mail : penglishuang1@163.com

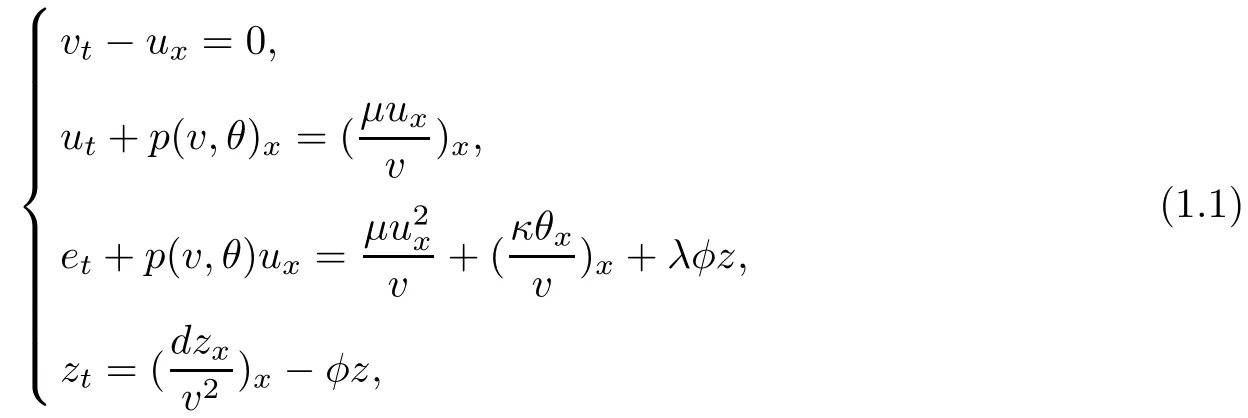
where x ∈ R is the Lagrangian space variable and t ∈ R+is the time variable. Here, the primary dependent variables v = v(t,x) > 0, u = u(t,x) and θ = θ(t,x) > 0 denote the specific volume, fluid velocity and absolute temperature, respectively. z = z(t,x) is the mass fraction of the reactant,while the positive constants d and λ are the specific diffusion coefficients and the difference in heat between the reactant and the product, respectively. The reaction rate function φ = φ(θ) is defined, from the Arrhenius law [2], by
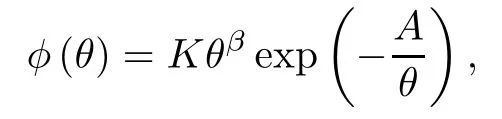
where positive constants K and A are the coefficients of the rate of the reactant and the activation energy, respectively. β is a non-negative number.
The positive constants μ and κ denote the viscosity coefficient and the heat conduction coefficient,respectively. The pressure p and the internal energy e are given by the state equation
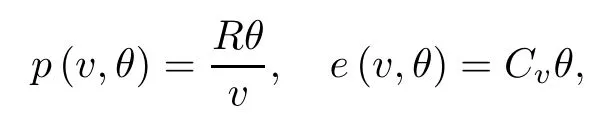
where R and Cvare the positive constants. We impose the following initial and far field conditions as:
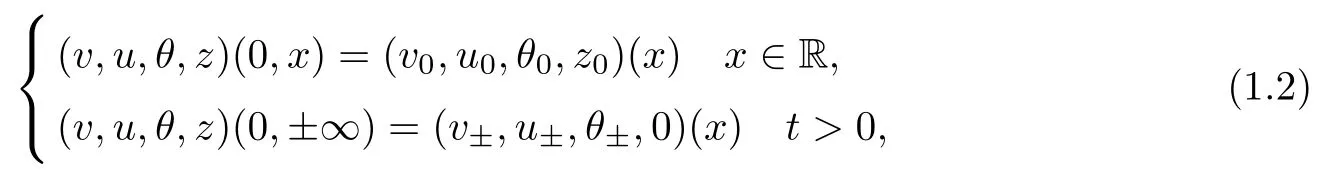
where v±>0,u±and θ±>0 are given constants,and where we assume infRv0>0,infRθ0>0 and (v0,u0,θ0,z0)(±∞)=(v±,u±,θ±,0) as compatibility conditions.
It is known that the large-time behavior of solutions of the Cauchy problem (1.1)–(1.2) is closely related to the Riemann problem of the compressible Euler system:

with the Riemann initial data
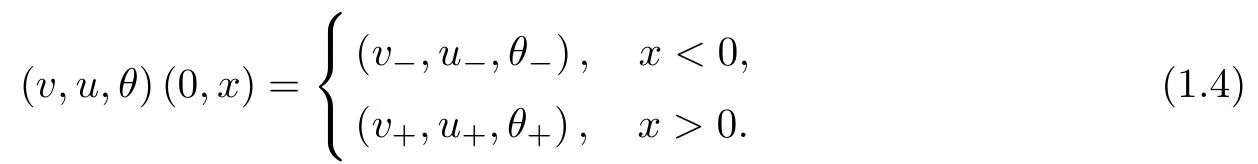
It is well-known that the above system has the three eigenvalues:
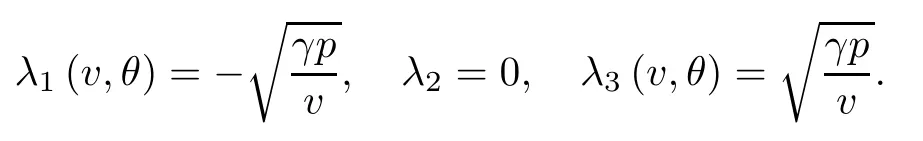
This implies that the first and third characteristic fields are genuinely nonlinear and that the second field is linearly degenerate. Then the basic Riemann solutions of the problem(1.3)–(1.4)are dilation invariant solutions: shock waves,rarefaction waves,contact discontinuities,and the linear combinations of these basic waves. In particular, the contact discontinuity solution of the Riemann problems (1.3) and (1.4) takes the following form [3]:
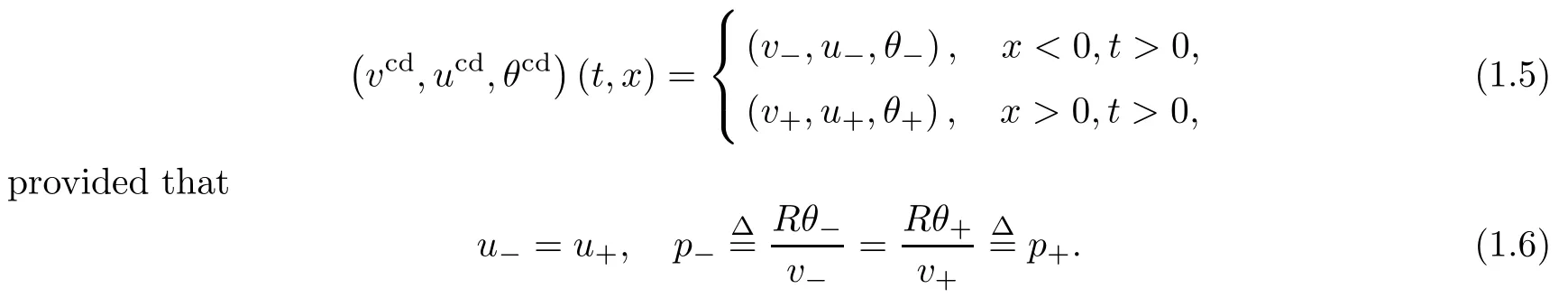
The viscous contact wave (V,U,Θ,Z)(t,x) with Z(t,x) = 0 corresponding to the contact discontinuity vcd,ucd,θcd,0 (t,x) becomes smooth and behaves as a diffusion wave, due to the effect of heat conductivity in the system (1.1).
As in[4],we can define the viscous contact wave(V,U,Θ)(t,x)as follows: since the pressure of the profile (V,U,Θ)(t,x) is expected to be almost constant, we set

Then the leading part of energy equation (1.1)3is
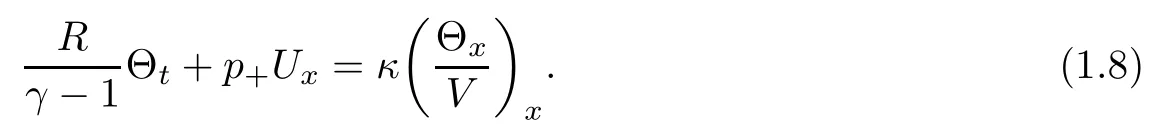
Using the equations (1.7), Vt=Uxand (1.8), we get a nonlinear diffusion equation
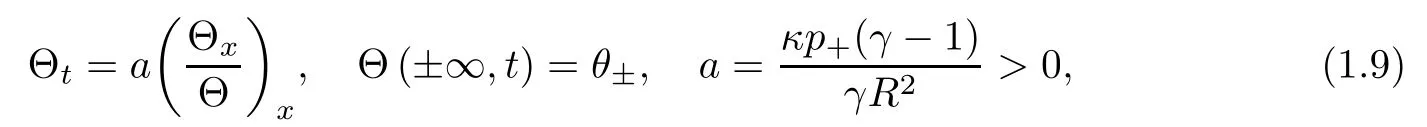
which has a unique self-similar solution Θ (t,x) = Θ (ξ),ξ =because of [5, 6]. Furthermore, Θ(ξ) is a monotone function, increasing if θ+> θ?and decreasing if θ+< θ?. On the other hand, there exists some positive constantsuch that, for δ =|θ+? θ?|≤Θ satisfies
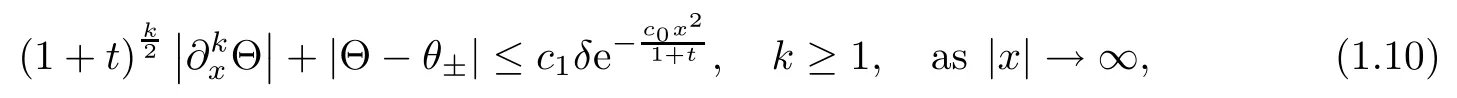
where c0and c1are two positive constants depending only on θ?andOnce Θ is determined,the viscous contact wave profile (V,U,Θ)(t,x) is defined as follows:

It is straightforward to check that (V,U,Θ) satisfies
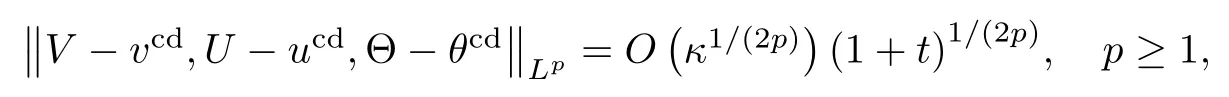
which means the nonlinear diffusion wave(V,U,Θ)(t,x)approximates the contact discontinuityto the Euler system (1.3) in the Lpnorm, and p ≥ 1 on any finite time interval as the heat conductivity coefficient κ tends to zero. It is easy to check that the viscous contact wave (V,U,Θ) satisfies the system
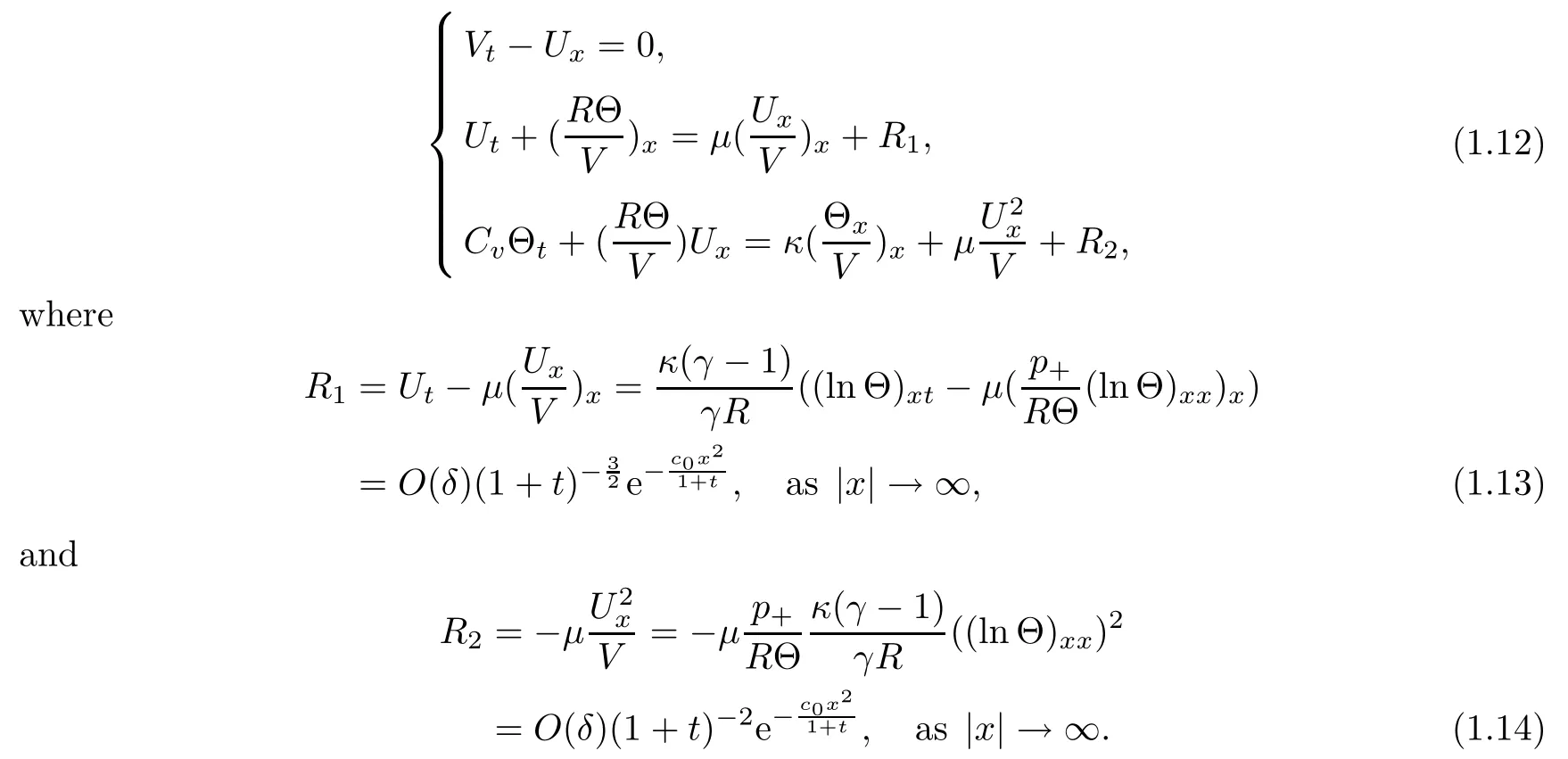
Throughout this article, we suppose that the pressure p′and the constant Cvare given by
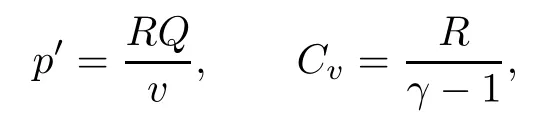
where γ >1 is the adiabatic exponent and
We are now in a position to state our main result. Let
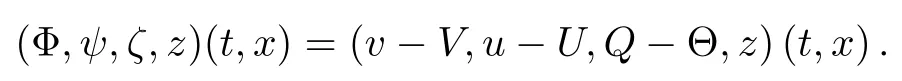
For interval I ? [0,∞), we define a function space
The main result of this article can be stated as the following theorem:
Theorem 1.1For any given (v?,u?,θ?), suppose that (v+,u+,θ+) satisfies (1.6). Let(V,U,Θ)(t,x) be the viscous contact wave defined in (1.11) with strength δ = |θ+? θ?| ≤Then there exist positive constants δ0and ε0such that if δ < δ0and the initial data(v0,u0,θ0,z0) satisfies
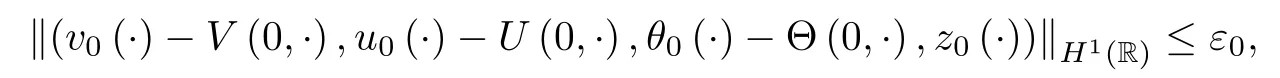
then the Cauchy problem(1.1)–(1.2)admits a unique global solution(v,u,θ,z)(t,x) satisfying(v ? V,u ? U,Q ? Θ,z)(t,x) ∈ X([0,∞)) and
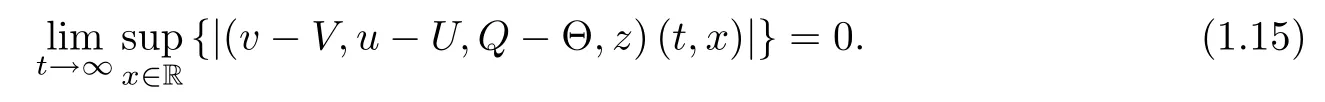
Now, we briefly recall some work related to this problem, and make some comments on the analysis that will be carried out in this article. The nonlinear stability of viscous contact waves has been studied by many authors. The stability of contact waves for solutions of systems of viscous conservation laws was first studied by Xin [7], who obtained the metastability of a weak contact discontinuity for the compressible Euler system with uniform viscosity. Later,Liu and Xin [8]showed the metastability of contact discontinuities for a class of general systems of nonlinear conservation laws with uniform viscosity, and this result was improved by Xin and Zeng in [9]. For the compressible Navier-Stokes system, the asymptotic stability of a viscous contact wave with a free boundary was first obtained by Huang,Matsumura,and Shi[10]using an elementary energy method in which the initial perturbation and the strength of the contact discontinuity are suitably small. The asymptotic stability of the linear combination wave of a viscous contact wave and the rarefaction waves for the Cauchy problem of the one-dimensional compressible Navier-Stokes system was obtained by Huang, Li and Matsumura in [1], provided the strength of the combination wave is suitably small. There are many interesting results in this aspect were obtained from [11–19]. For the corresponding results performing large initial perturbation, see [20–22]and the references cited therein.
The mathematical study of viscous compressible radiative and reactive gas has attracted a lot of interest in recent years. For the radiative(a′>0) case, the well-posedness of global classical solutions was established by [23–25]for the Dirichlet-Neumann boundary conditions and by[23, 26–29]for the free and pure Neumann boundary conditions in one-dimensional bounded domains. The exponential stabilization of solutions was studied by Ducomet and Zlotnik[2,30]by constructing new global Lyapunov functionals. The global existence and large-time behavior of solutions to the Cauchy problem of one-dimensional viscous radiative and reactive gas with large initial data were obtained by Liao and Zhao [31]. For more than one dimension,Donatelli and Trivisa [32]showed the global existence of variational solutions. For a bounded annular domain, Zhang [33]obtained that spherically and cylindrically symmetric solutions exist globally-in-time for the initial-boundary value problem. Other results were demonstrated in [34, 35]with large initial data. The global well-posedness of spherically symmetric large solutions to viscous radiative and reactive gas in an exterior domain was studied by Liao,Wang and Zhao [36].
For the non-radiative(a′=0)case,the model of a compressible Navier-Stokes system for a reacting mixture was first proposed by Williams in [37]. The existence and asymptotic behavior of global solutions to the compressible Navier-Stokes equations for a reacting mixture with discontinuous reacting rate functions were studied by Chen [38]. The existence and dynamic behavior including stability, regularity, and large-time behavior of discontinuous solutions to the Navier-Stokes equations for one-dimensional reacting compressible fluids with discontinuous initial data of large oscillation were established by Chen, Hoff and Trivisa [39, 40]. For one-dimensional unbounded domains, the global existence and large-time behaviour of global solutions to the compressible Navier-Stokes equations for a reacting mixture were proved by Li [41]. Recently, Xu and Feng proved the nonlinear stability of rarefaction waves for onedimensional compressible Navier-Stokes equations for a reacting mixture in [42].
In this article, we shall show the asymptotic stability of a viscous contact wave for the Cauchy problem of the one-dimensional compressible Navier-Stokes equations for a reacting mixture,provided the strength of the contact discontinuity is suitably small. The main difficulty we encounter here is due to the appearance of the term λφz,which will make Lemma 3.1 invalid.In order to overcome this difficulty, we can eliminate this term by multiplying (1.1)4by λ and adding it to (1.1)3. After stating some notations, we will reformulate the original problem and give some preliminary lemmas and a priori estimates of solutions to the Cauchy problem (2.2)in Section 2. Finally, Section 3 completes the proof of Theorem 1.1.
NotationThroughout this article, several positive generic constants are denoted by C, c without confusion. For functional spaces, Hl(R) denotes the l-th order Sobolev space with its norm
2 Reformation
To make it more convenient to prove Theorem 1.1, in this section, we will reformulate problem(1.1). Multiplying(1.1)4by λ and adding it to(1.1)3,the system(1.1)can be rewritten as

so we have, from (1.12) and (2.1), that
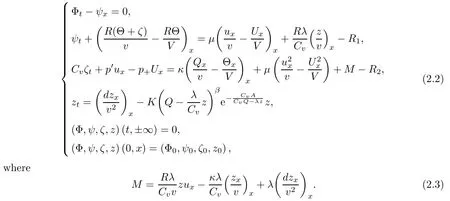
We derive an elementary inequality concerning the heat kernel which will play an essential role later. For α>0, we define
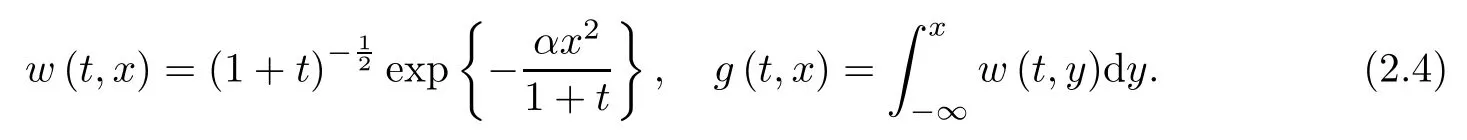
It is easy to check that
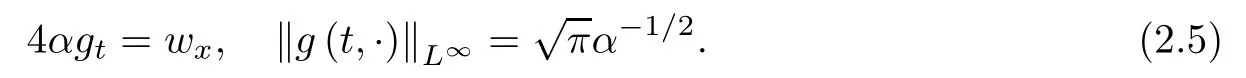
Then we have
Lemma 2.1(see [1]) For 0 Then the following estimate holds: For the proof Lemma 2.1, one refers to [1]. Next, we summarize some basic properties of the viscous contact wave (V,U,Θ). Lemma 2.2(see [11]) Assume that δ = |θ+? θ?| ≤for some positive constantThen there exist two positive constants,c0and C, such that the viscous contact wave(V,U,Θ)satisfies the following estimates: Lemma 2.2 can be proved directly from Equations(1.10)and(1.11);the details are omitted here. Now, we give a Sobolev inequality without proof. Lemma 2.3(see [11]) For any f(x)∈H1(R), we have Finally, we give the range of z(t,x). Here we use the same method as in [38]to prove Lemma 2.4. Lemma 2.4For any (t,x)∈ [0,T]× R, we have 0 ≤ z(t,x)≤ 1. ProofSet Y =ze?αt, and that α >0 is constant. Then Y (t,x) satisfies We claim that Y (t,x)≥0. On the contrary, there exists (t0,x0)∈ [0,T]×R such that We have However, This is a contradiction. Thus, it follows that On the other hand, we obtain from Proposition 2.1 below that This completes the proof of Lemma 2.4. We first state a result for the existence of the local in time solutions to Cauchy problem(2.2), the proof of which is similar to that of theorem 2 in [38], and thus omitted here for brevity. Proposition 2.1(Local existence) Under the assumptions of Theorem 1.1, there exist positive constants ε1(≤ ε0) and C1(C1ε1≤ ε0), iffor any constant 0 < M0<ε1, and there exists a positive constant t1= t1(M0) > 0 such that ifthen the Cauchy problem (2.2), via replacing t=0 by t= τ, admits a unique solution (Φ,ψ,ζ,z) ∈ X([τ,τ +t1]) satisfying In order to prove the global existence of the Cauchy problem(2.2),we only have to establish the following a priori estimates: Proposition 2.2(A priori estimate) There exist positive constants ε0and C, such that, for T >0 and (Φ,ψ,ζ,z)∈ X([0,T]) satisfying we have the estimate Once Proposition 2.2 is proved, we can extend the unique local solution (v,u,θ,z), which we have obtained in Proposition 2.1, to T =∞. Estimating (2.12), together with the equation(2.2), implies that which, along with (2.12) and the Sobolev inequality, easily leads to the asymptotic behavior of the solutions, that is, (1.15). From now until the end of this paper, we always assume that ε0+ δ0≤ 1. Proposition 2.2 is an easy consequence of the lemmas to follow. In this section we will provide some a priori energy estimates for the solutions to system(2.2). We first give the following key estimate: Lemma 3.1For T > 0 and (Φ,ψ,ζ,z)∈ X([0,T]) satisfying (2.11) with suitably small ε0+ δ0, we have, for t ∈ [0,T], that ProofMultiplying (2.2)1by ?RΘ(v?1? V?1), (2.2)2by ψ, (2.2)3by ζQ?1, and (2.2)4by z, then adding the resulting equations together, we have Noticing that Φ (1)= Φ′(1)=0 and Φ′′(s)>0, there exist positive constants C2and C3such that Now, using Lemma 2.3, assumption (2.11), Hlder inequality and Young’s inequality, we have Thus, we get, from (3.7)–(3.9), that After integrating (3.4) on (0,t)×R, we get where in the last inequality, we have used due to the fact that which comes from(1.10). Lemma 3.1 thus follows directly from(3.11)and the following Lemma 3.2 by choosing α =c2/4 in (3.14) and δ suitably small. Lemma 3.2For α ∈ (0,c2/4]and w defined in (2.4), there exists some positive constant C depending on α such that the following estimate holds: ProofThe proof of (3.17) is divided into the following two parts: and, for any η >0, In fact, adding (3.16) to (3.15) and taking first η and then δ suitably small thus implies (3.14)easily. We first prove (3.15). Denotingwe then have Rewriting equation (2.2)2as and multiplying equation (3.18) by (Rζ ? p+Φ)vf and integrating the resulting equation over R leads to Now, we estimate the term Ji,i = 1,2,··· ,7 term by term. First, we have, from equations(2.2)1and (2.2)3, that Thus, it follows from equations (3.20) and (2.2)1that Because of the proof of Lemma 5 in [1], the following estimates hold: We deduce from equations (2.8), (3.12), (3.13), (3.17) and the Sobolev inequality (2.9) that Finally, J7can be controlled by Combining all the estimates (3.19) and (3.21)–(3.26), and integrating the resulting equation with respect to t over (0,t), one can obtain equation (3.15). After getting (3.15), we are supposed to use Lemma 2.1 to obtain (3.16) and finish the proof of Lemma 3.2. We take h=Rζ+(γ ?1)p+Φ in Lemma 2.1 and use (3.20) to derive Now, we estimate Ji,i =8,9,··· ,14 as follows: we have from equations (2.5), (2.8), (2.9) and(3.13) and the Cauchy inequality that For the estimate of J8, noticing that Rζ ? p+Φ =h ? γp+Φ, we deduce from equations (2.2)1,(2.5) and (3.20) that Finally, in a fashion similar to the estimate of equation (3.32)–(3.33), we have Combining equations (3.29)–(3.40), we obtain from equation (3.28) that Equation (3.16) thus follows from Lemma 2.1 and (3.41). This completes the proof of Lemma 3.2. Lemma 3.3Suppose that (Φ,ψ,ζ,z) ∈ X([0,T]) satisfies (2.11) with suitably small ε0+δ0. Then it holds, for t ∈ [0,T], that ProofWe rewrite equation (2.2)2as where we have used the following simple fact: due to vt=ux. Multiplying (3.43) byusing Φt= ψx, and noticing that we have Using (2.8) and (2.9), we obtain by direct calculation that The Cauchy inequality leads to The estimate (1.10) yields that Lemma 3.3 thus follows directly from Lemma 3.1 and (3.14), (3.44)–(3.49), by first choosing η suitably small and then δ suitably small. Lemma 3.4Suppose that (Φ,ψ,ζ,z) ∈ X([0,T]) satisfies (2.11) with suitably small ε0+δ0. Then it holds, for t ∈ [0,T], that ProofMultiplying (2.2)2by ?ψxx, we have Using (2.9) and (3.13), we obtain, by direct calculation, that The estimate (3.42) yields that which, as well as (1.10), leads to where we have used due to (1.10). Integrating(3.51)over R×(0,t),using(3.52)and(3.53),and first choosing η suitably small and then δ suitably small, we can obtain equation (3.50). This completes the proof of Lemma 3.4. Lemma 3.5Suppose that (Φ,ψ,ζ,z) ∈ X([0,T]) satisfies (2.11) with suitably small ε0+δ0. Then it holds, for t ∈ [0,T], that ProofMultiplying equation (2.2)3by ?ζxx, we obtain Using Lemma 2.3, (2.11), the Hlder inequality and the Young’s inequality, we have Thus, we get, from (3.57)–(3.59), that Then,using the same argument as the one previous,and integrating(3.55)over R×(0,t),using(3.60), and first choosing η suitably small and then δ suitably small, one can obtain equation(3.54). This completes the proof of Lemma 3.5. The next Lemma is devoted to controlling the term Lemma 3.6Suppose that (Φ,ψ,ζ,z) ∈ X([0,T]) satisfies (2.11) with suitably small ε0+δ0. Then it holds, for t ∈ [0,T], that ProofMultiplying (2.2)4by ?zxx, we have We have by Lemma 2.3, (2.11), the Hlder inequality and Young’s inequality that Integrating(3.62)over R×(0,t),using(3.63)and(3.64),and first choosing η suitably small and then δ suitably small, one can obtain equation(3.61). This completes the proof of Lemma 3.6. Thus, we finish the proof of Proposition 2.2,and so the proof of Theorem 1.1 is completed. AcknowledgementsThe author is grateful to Associate Professor Wenjun Wang for his valuable suggestions, and for many fruitful discussions on the topic of this article.
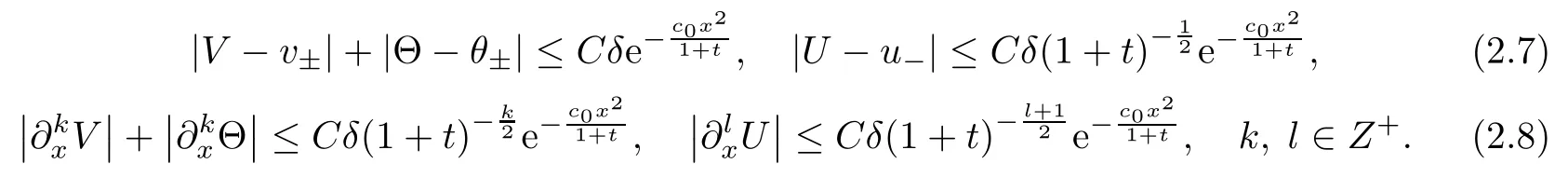

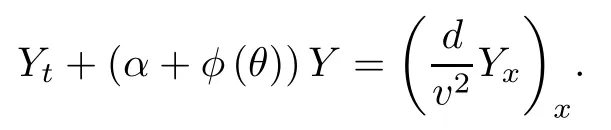
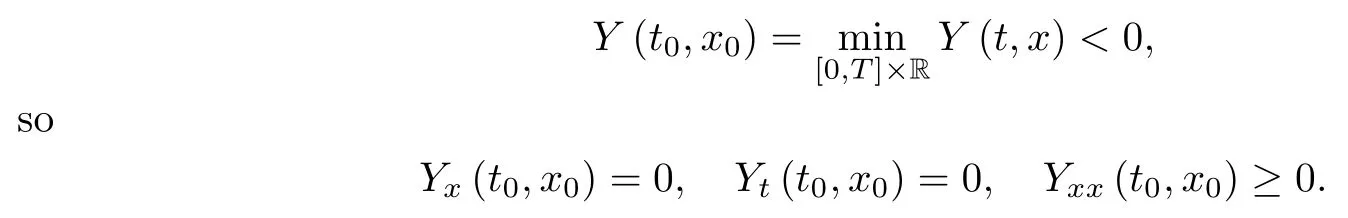
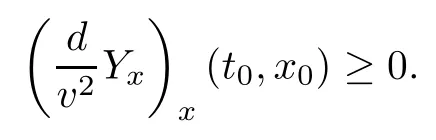
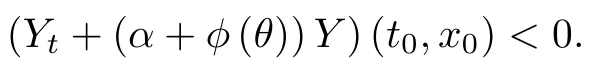
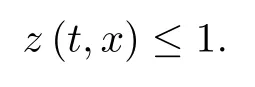
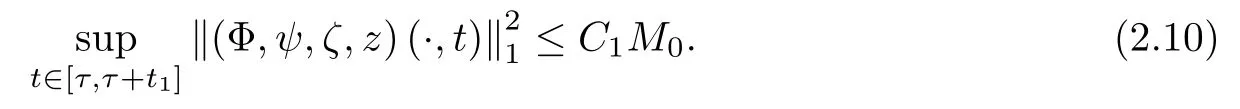
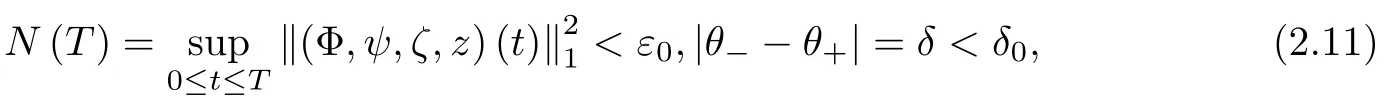
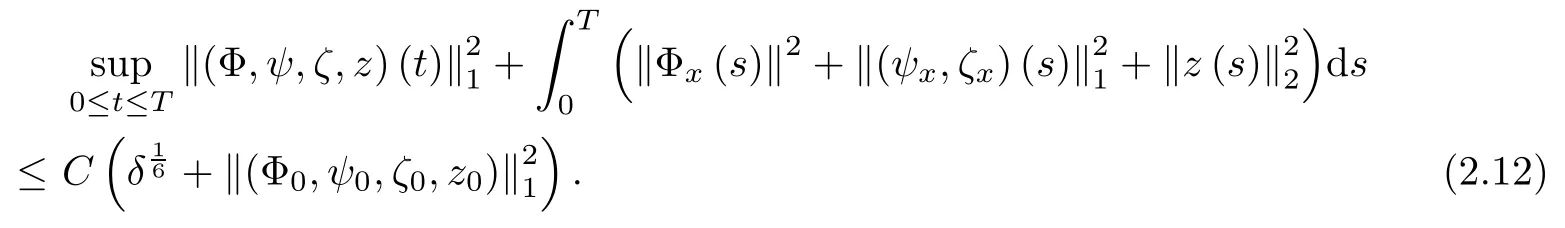
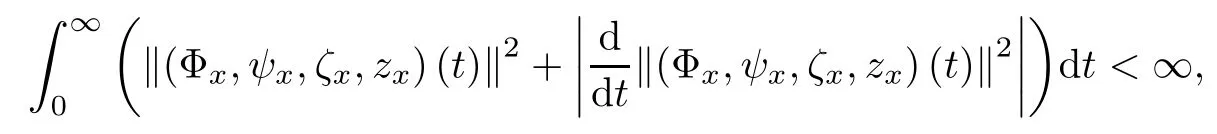
3 Energy Estimates
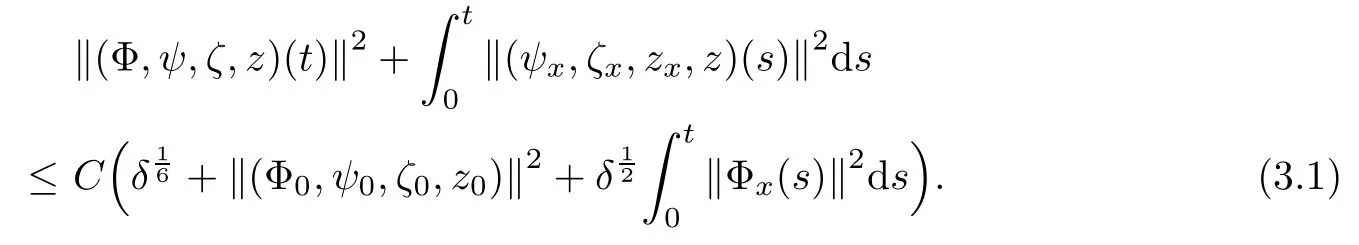

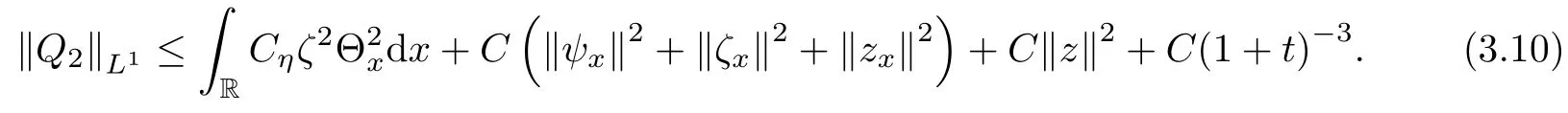
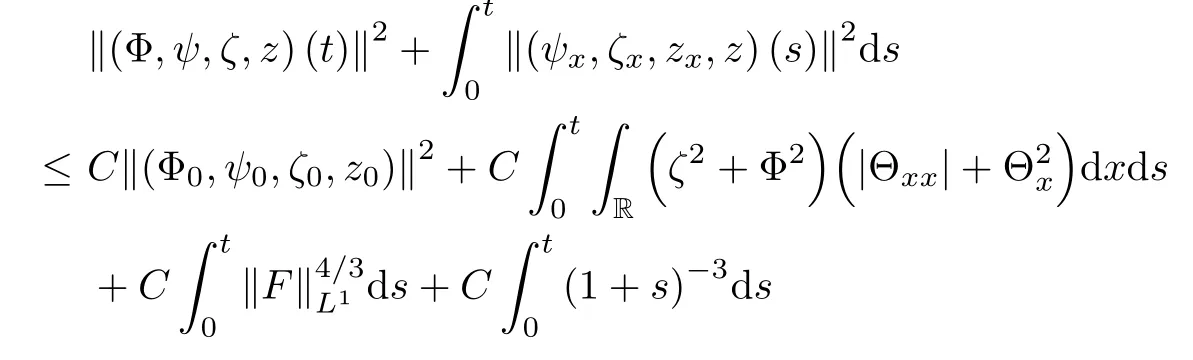
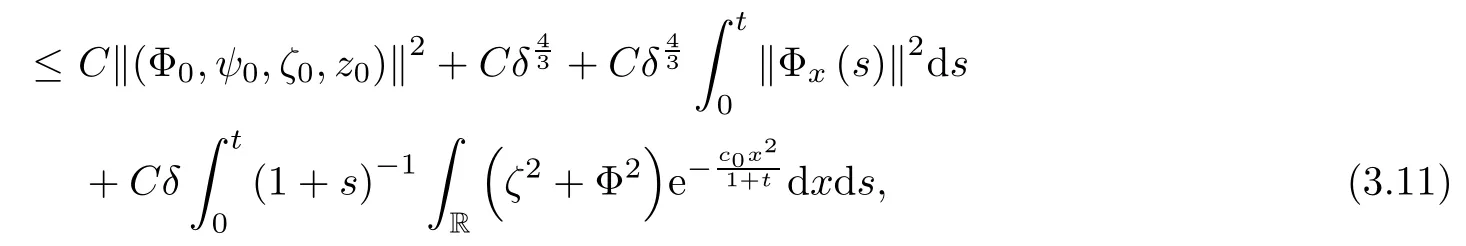
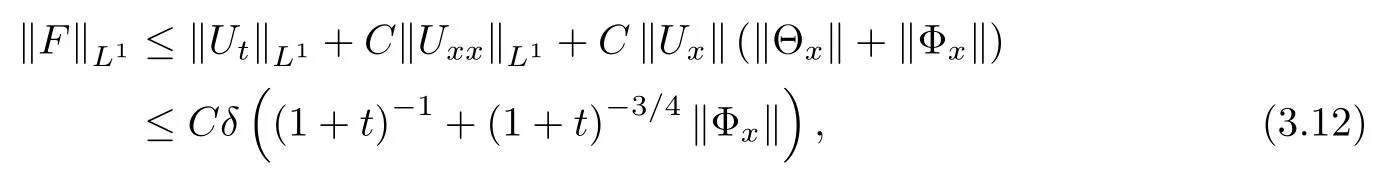
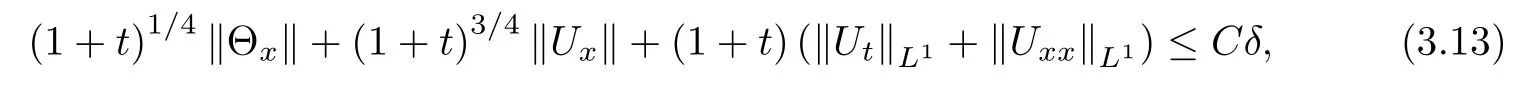
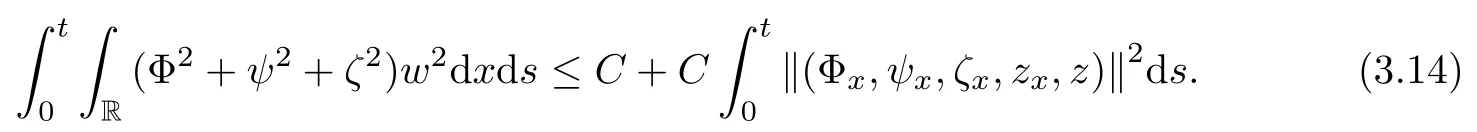
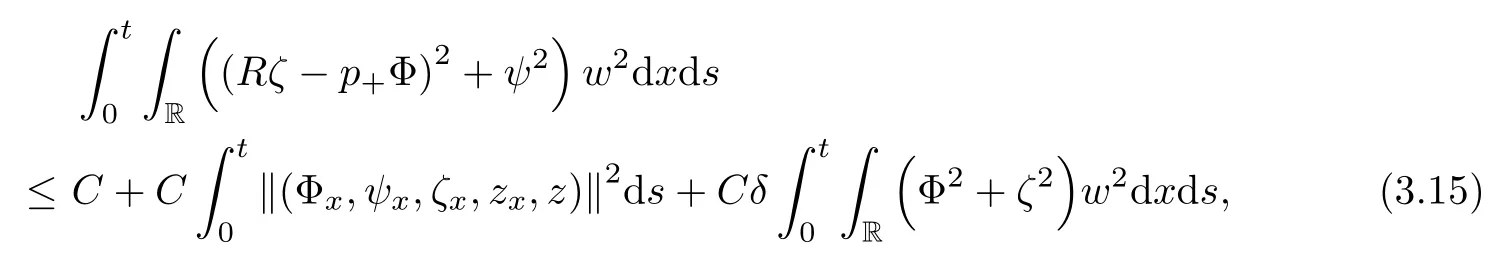
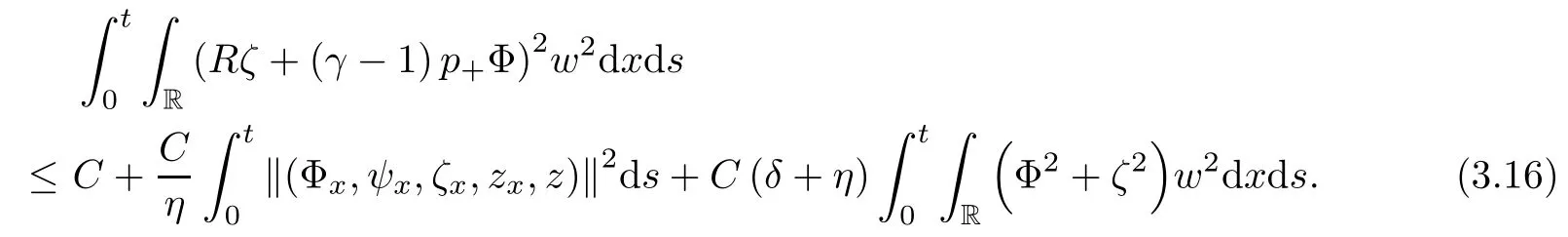
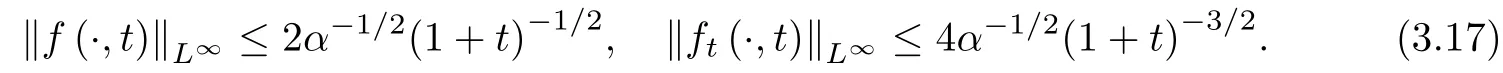
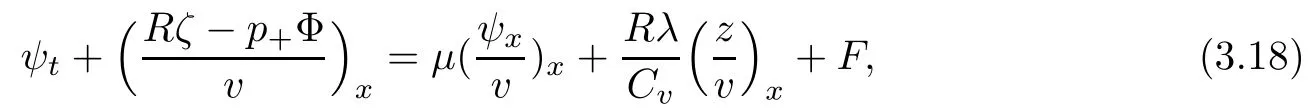
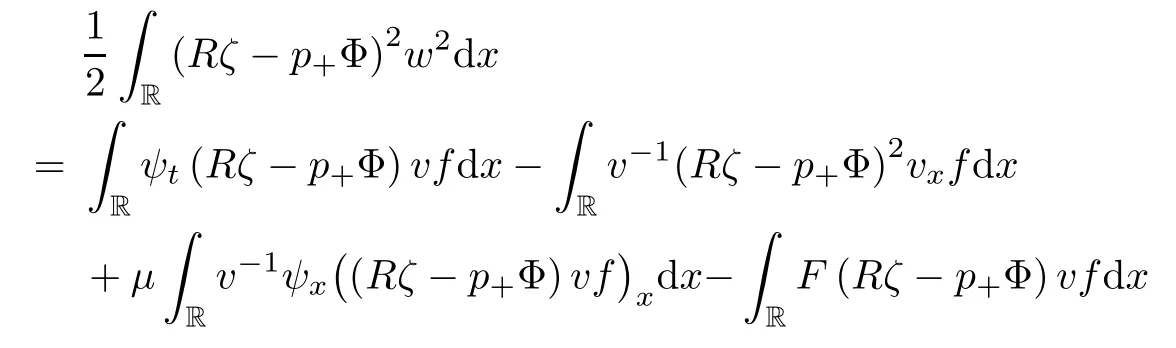
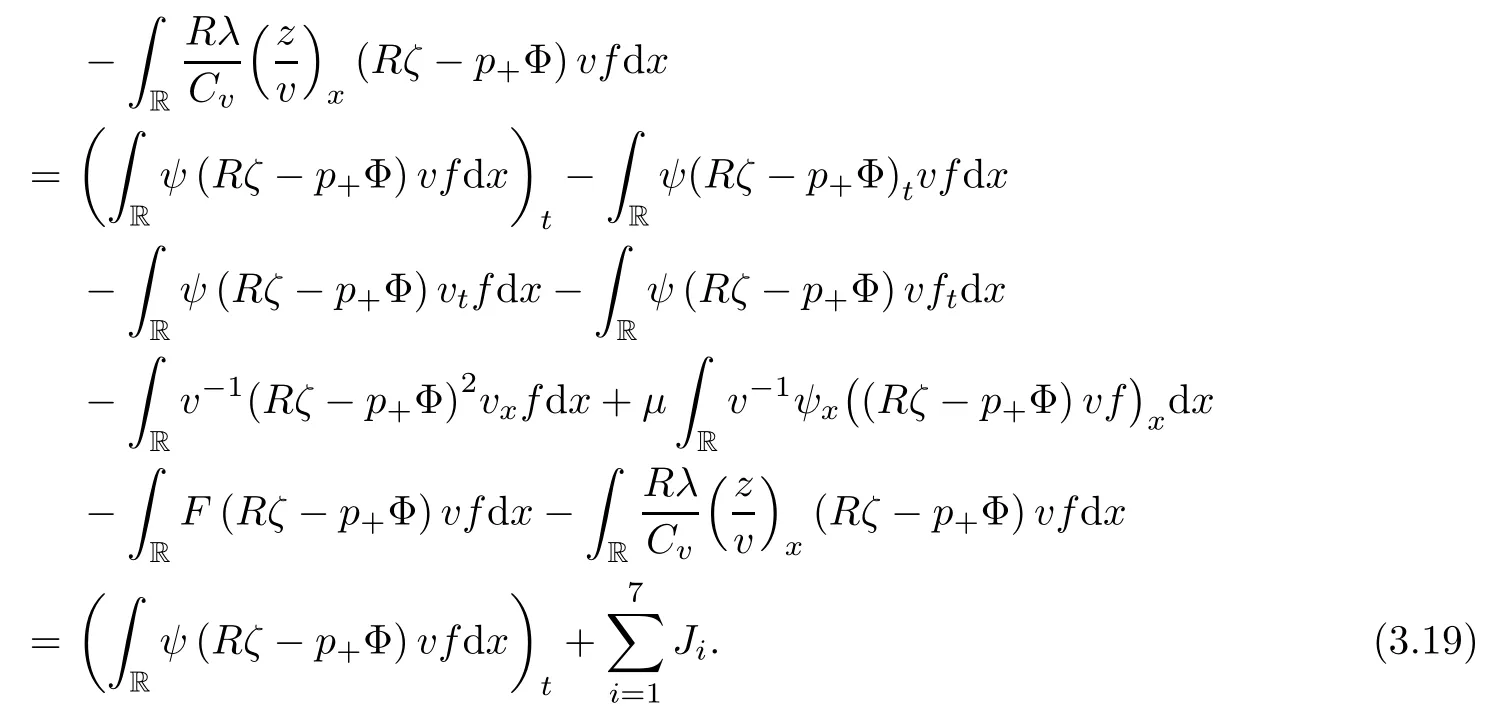
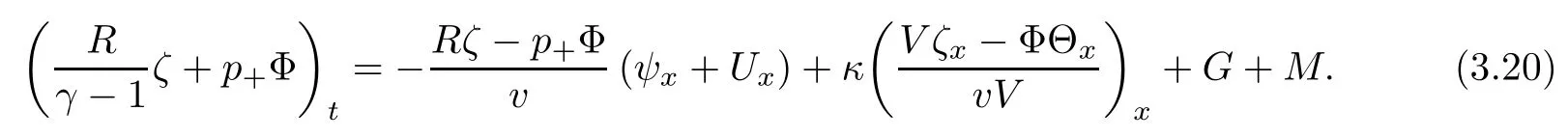
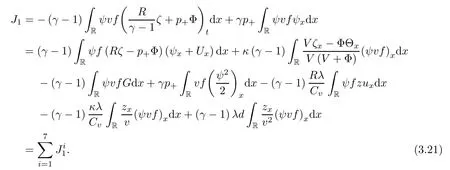
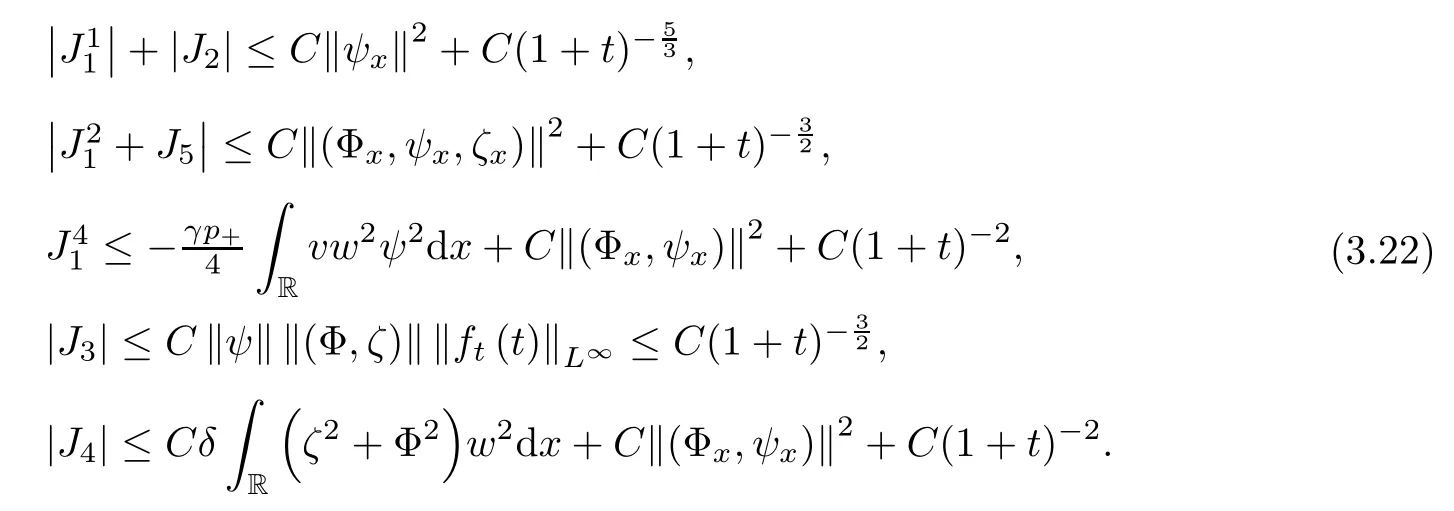
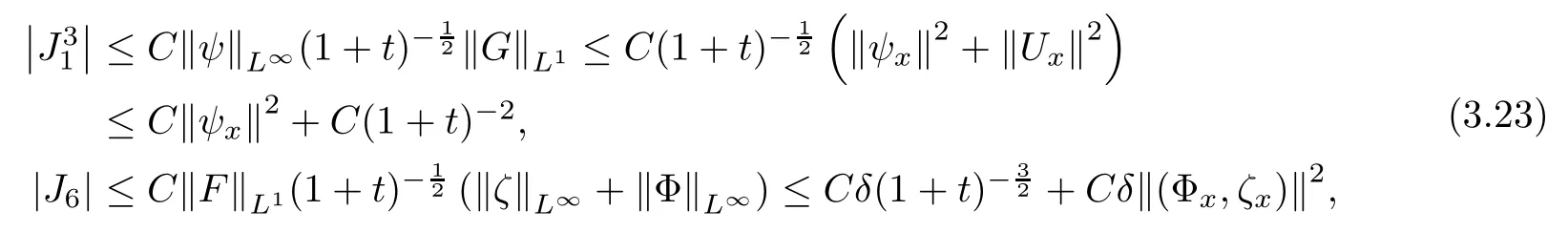
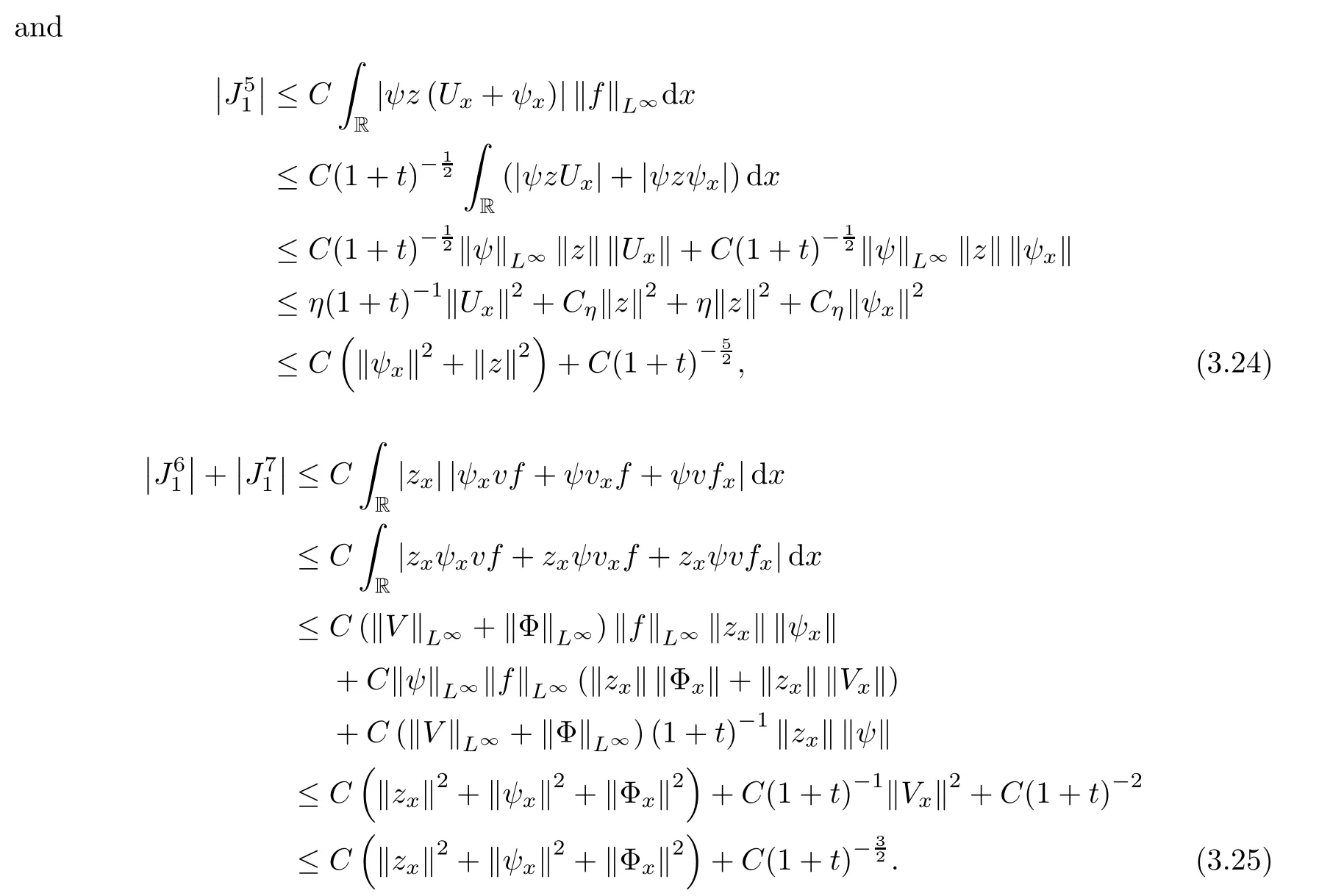
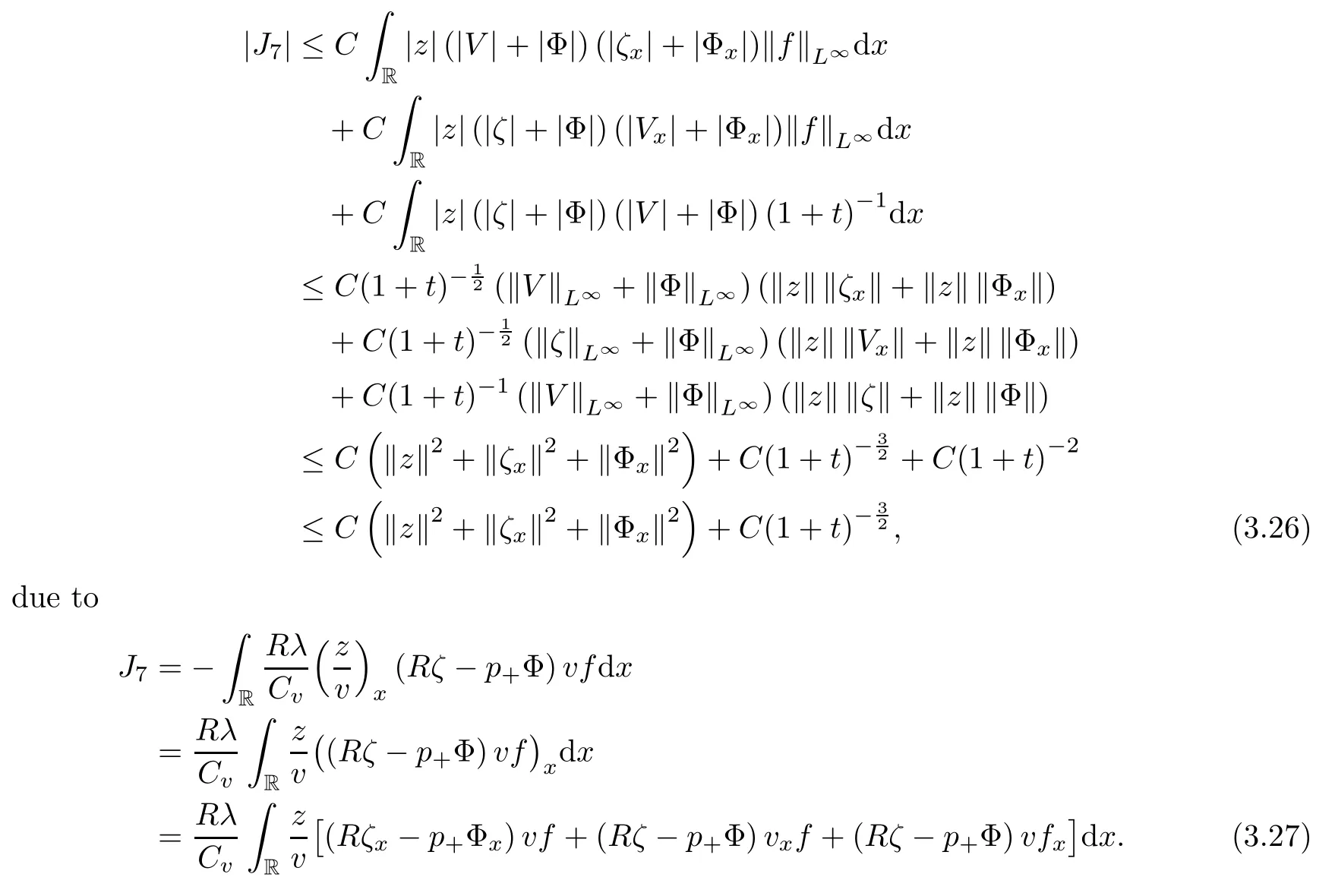
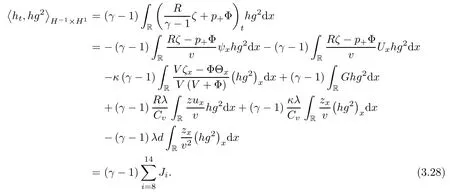
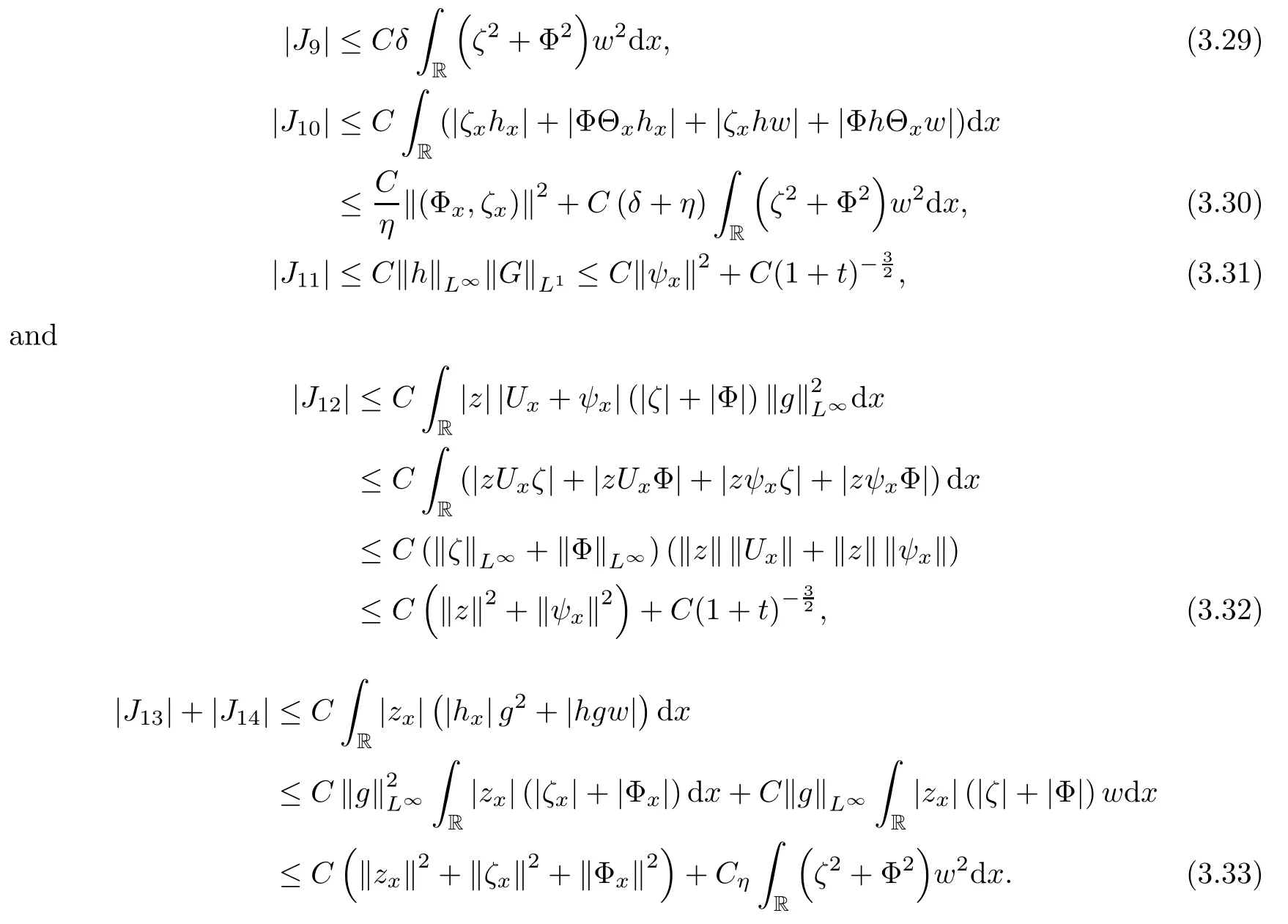
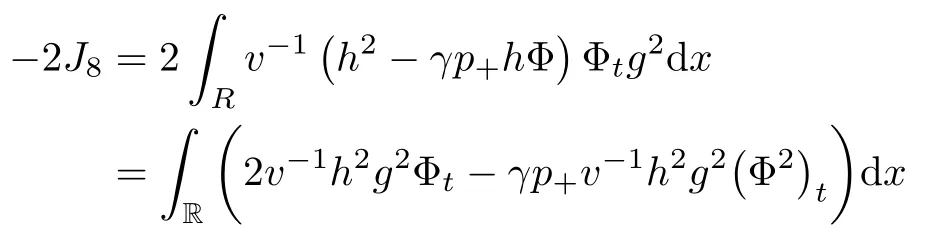
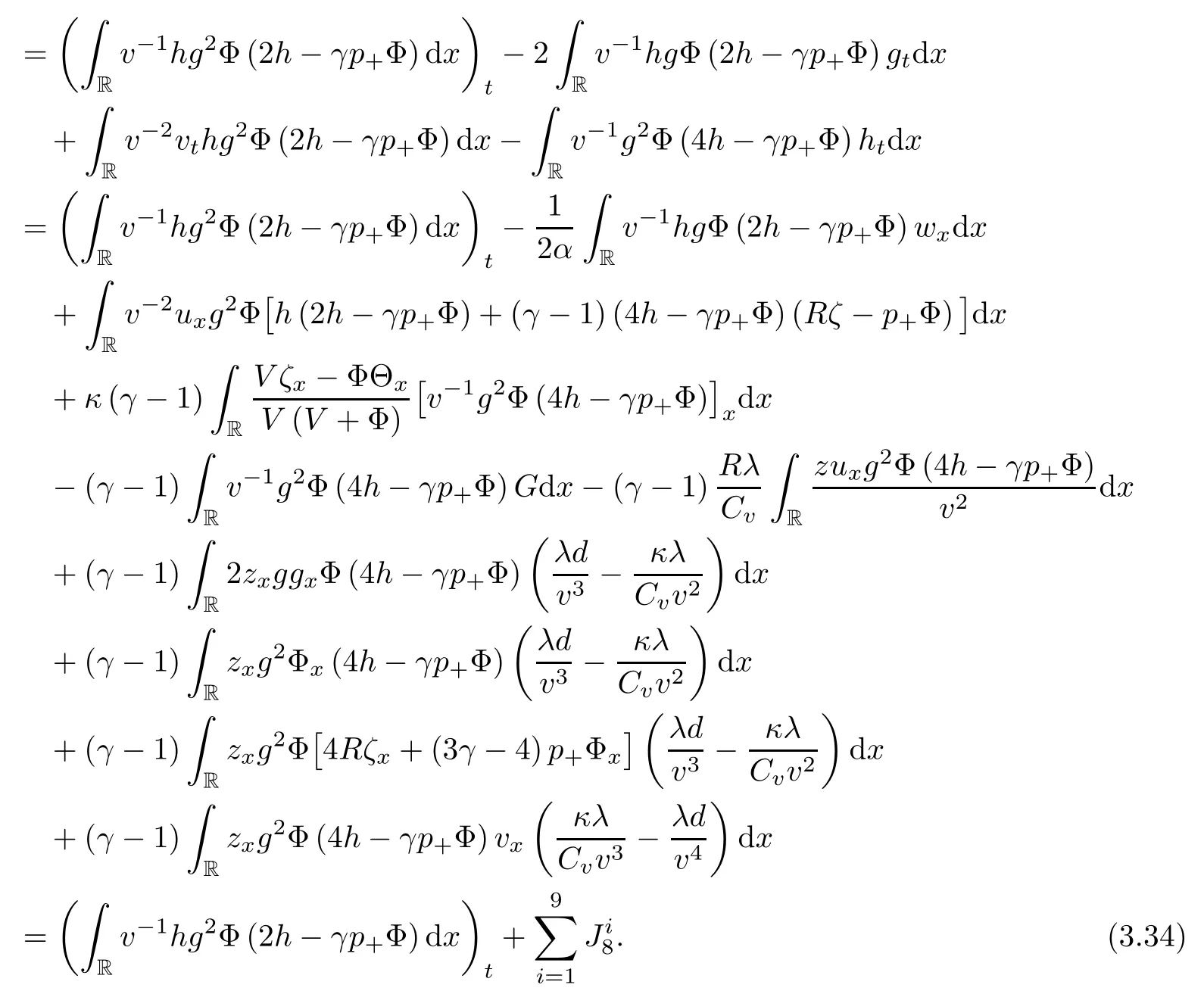
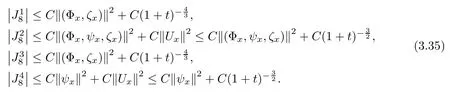
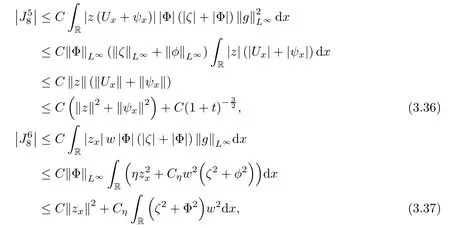
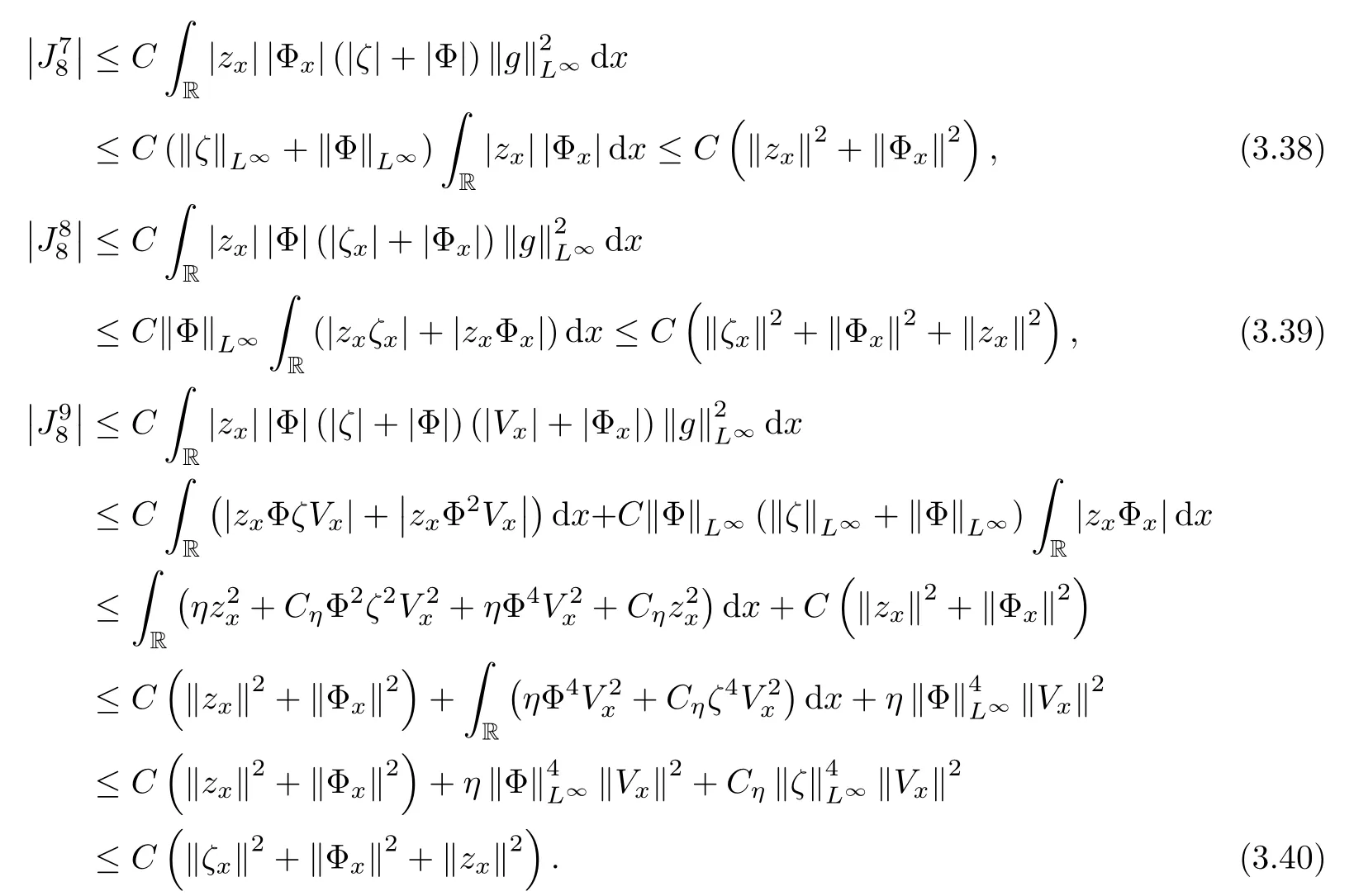
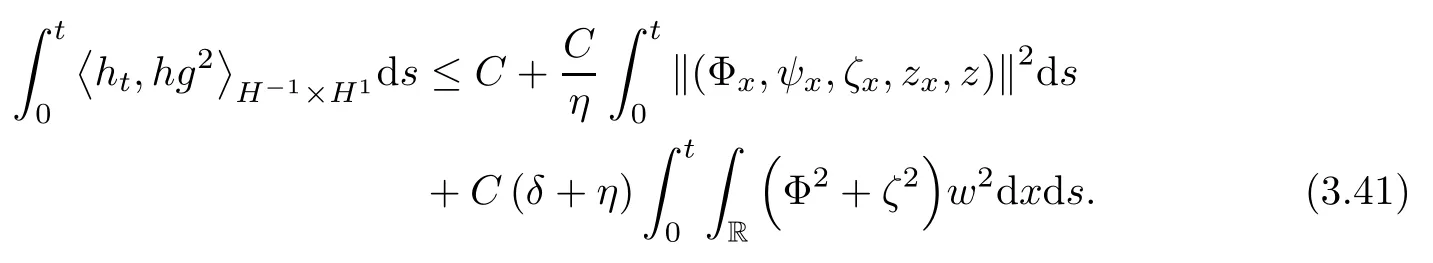
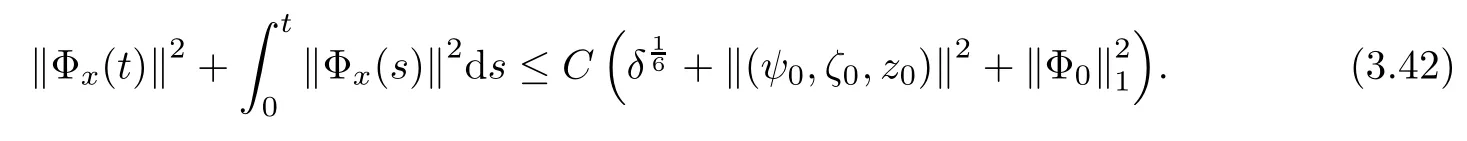
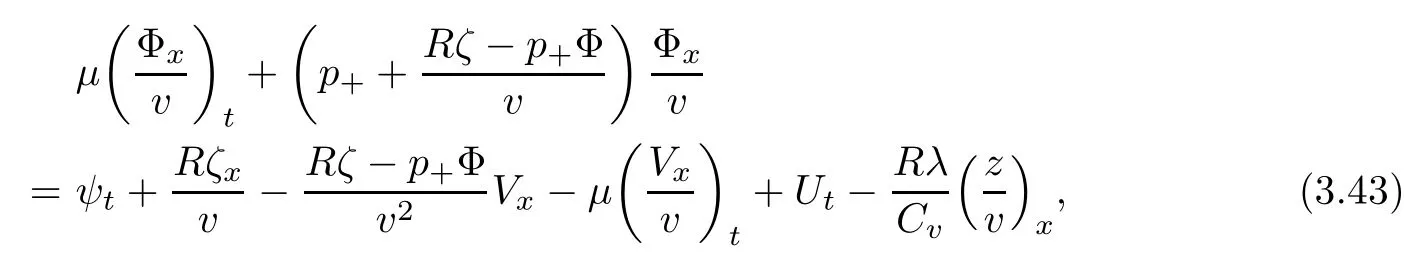
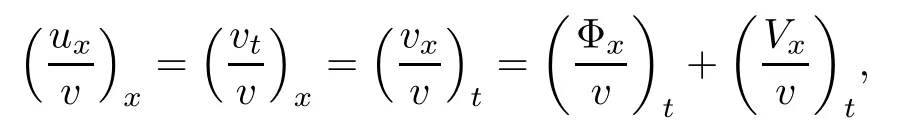
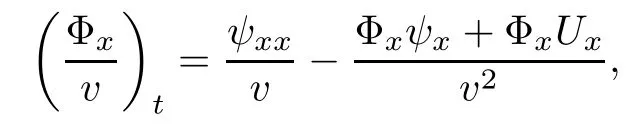
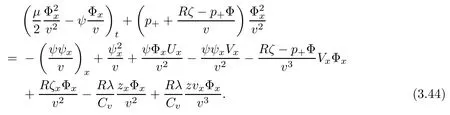
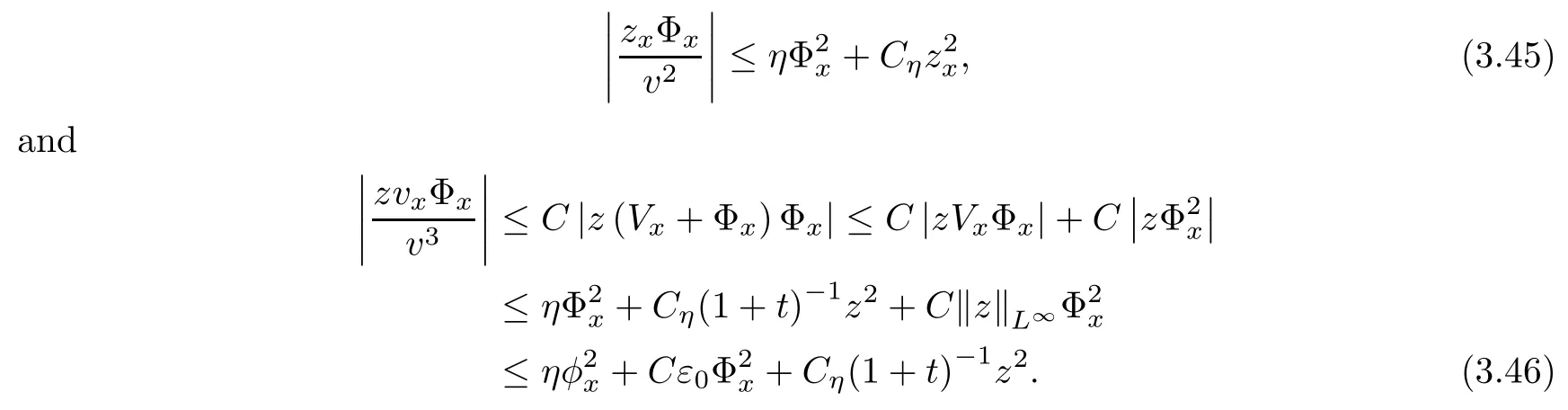
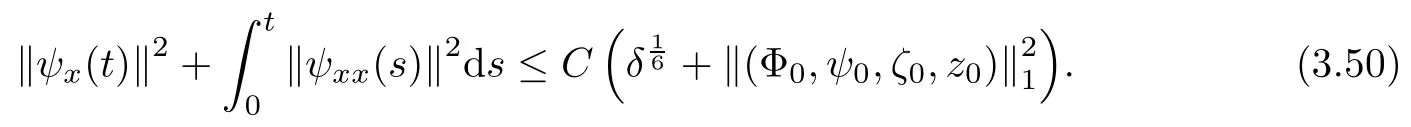
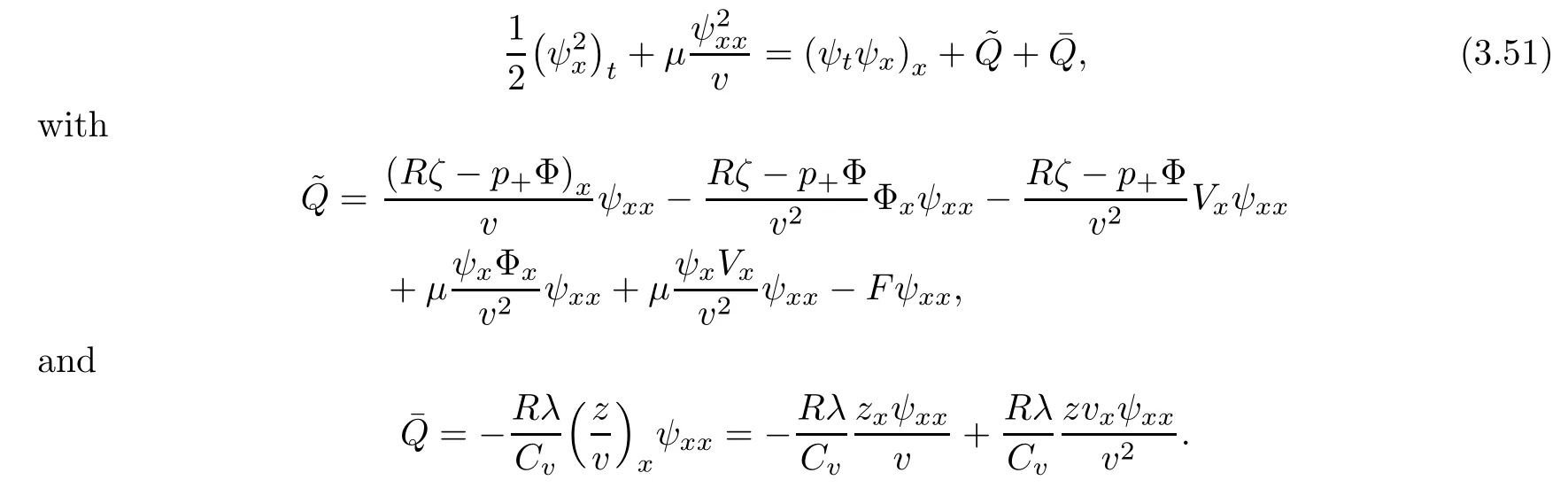
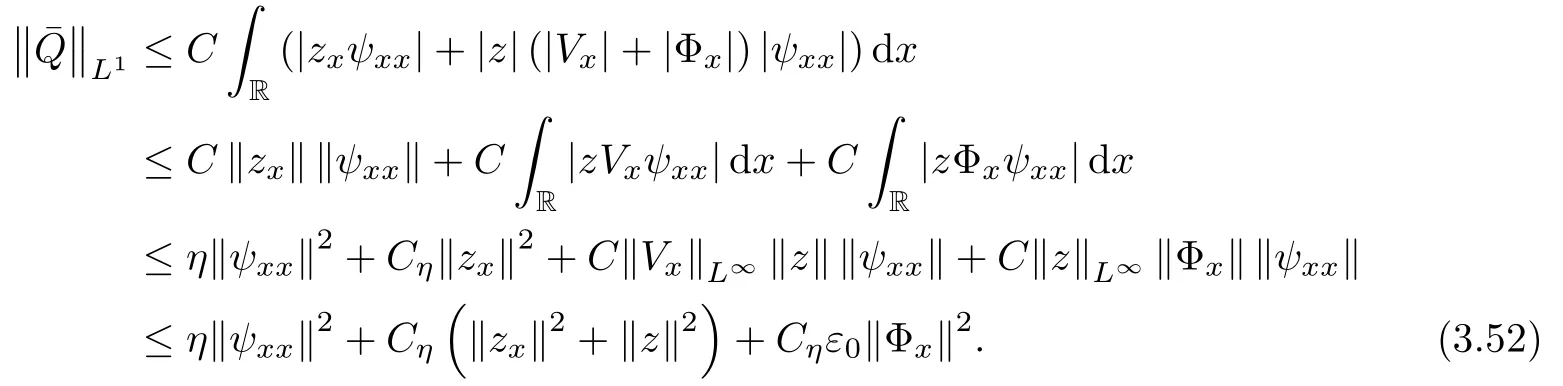
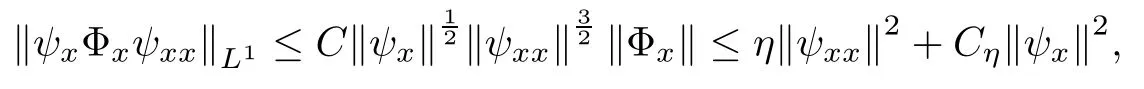
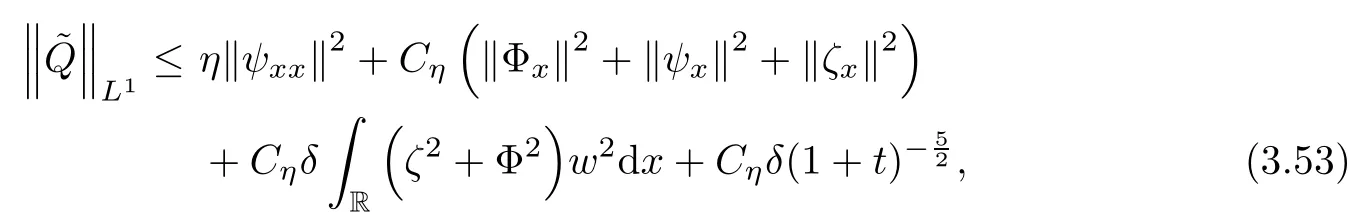
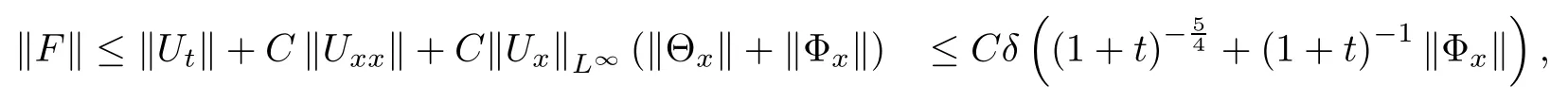
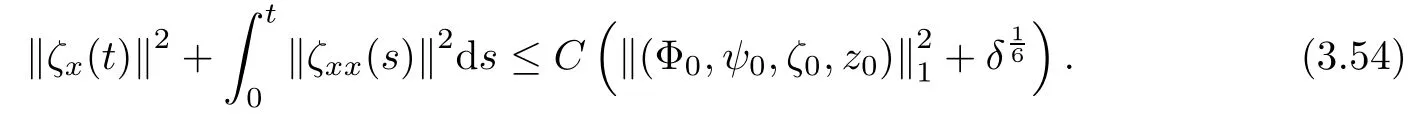

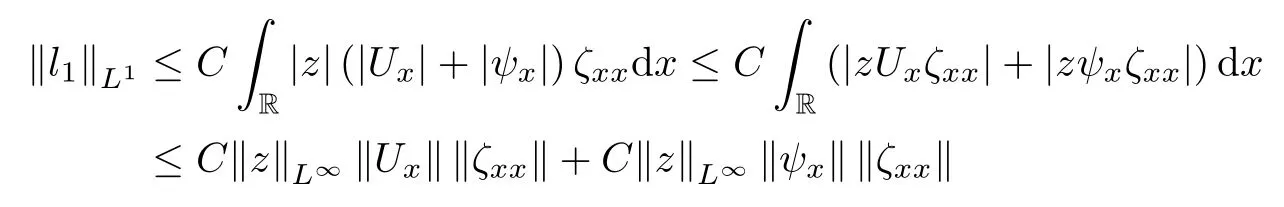
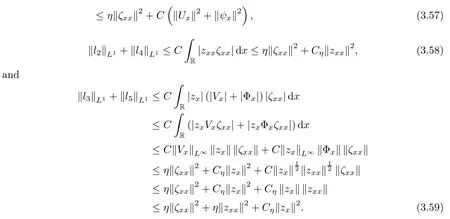
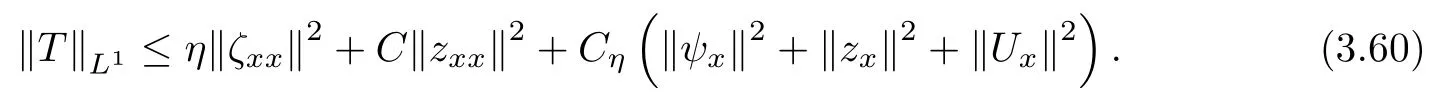
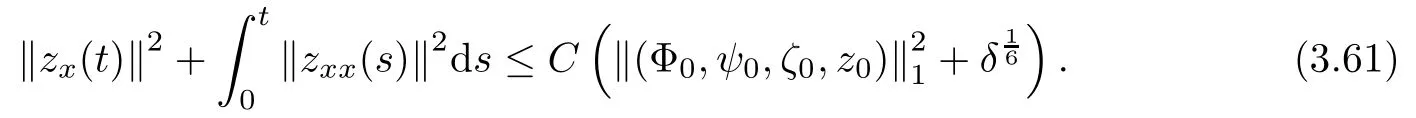
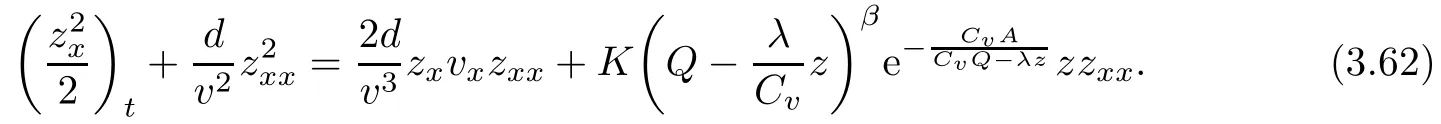
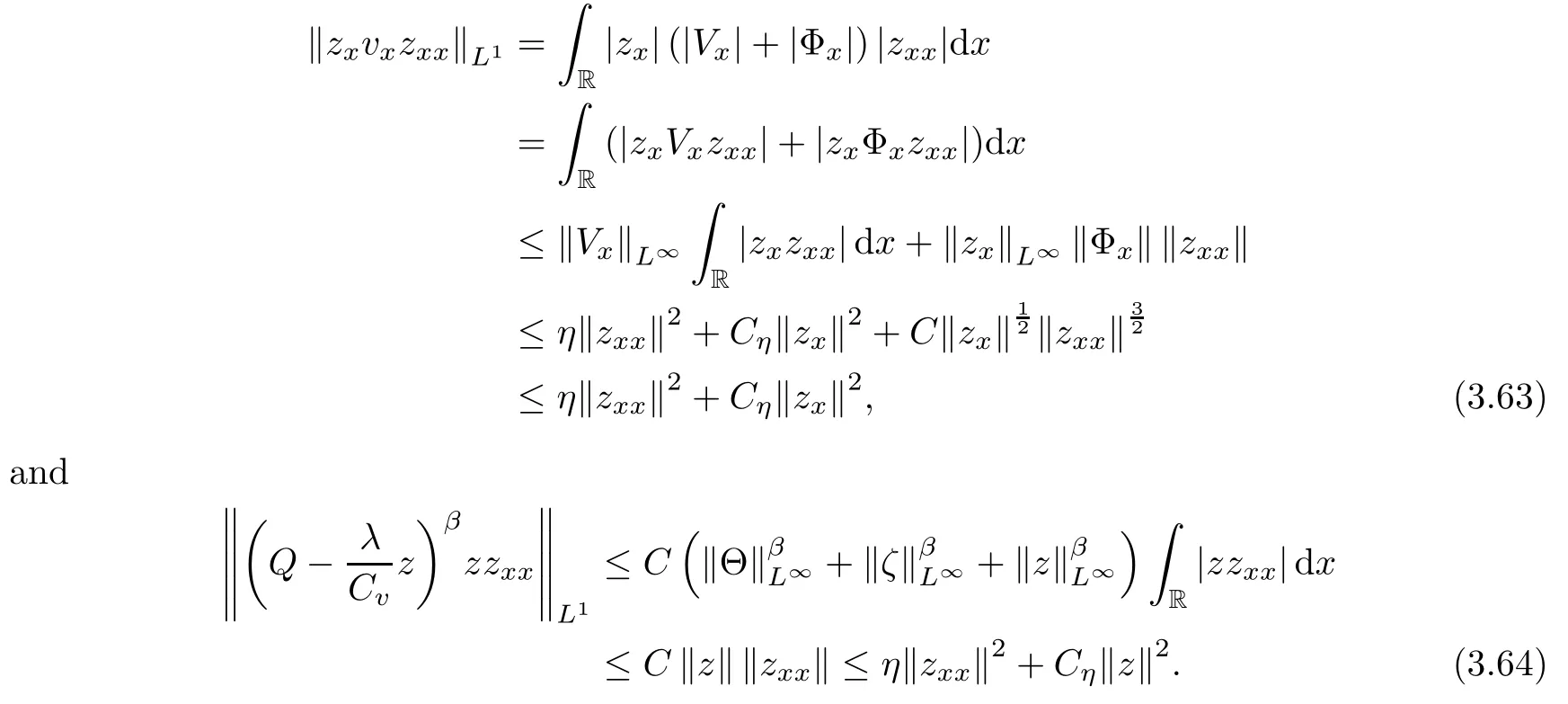
 Acta Mathematica Scientia(English Series)2020年5期
Acta Mathematica Scientia(English Series)2020年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RETRACTION NOTE: “MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD”Acta Mathematica Scientia, 2020,40B(4):614–624
- DYNAMIC ANALYSIS AND OPTIMAL CONTROL OF A FRACTIONAL ORDER SINGULAR LESLIE-GOWER PREY-PREDATOR MODEL?
- POSITIVE SOLUTIONS AND INFINITELY MANY SOLUTIONS FOR A WEAKLY COUPLED SYSTEM?
- PARAMETERS IDENTIFICATION IN A SALTWATER INTRUSION PROBLEM?
- A LEAST SQUARE BASED WEAK GALERKIN FINITE ELEMENT METHOD FOR SECOND ORDER ELLIPTIC EQUATIONS IN NON-DIVERGENCE FORM?
- EXISTENCE AND CONCENTRATION BEHAVIOR OF GROUND STATE SOLUTIONS FOR A CLASS OF GENERALIZED QUASILINEAR SCHRDINGER EQUATIONS IN RN?
