Department of Thermophysics,Moscow State Technical University N E Bauman,Moscow 105005,Russia

Abstract

Keywords:RF-ICP torch,dynamic heating,thermal destruction,hydrogen volume fraction,optimal injection conditions

1.Introduction

At present,high purity quartz(HPQ)concentrate has become one of the key strategic minerals with applications in hightech industries that include semiconductors,high temperature lamp tubing,telecommunications and optics,microelectronics,and solar silicon applications[1-3].One of the most promising technologies for producing HPQ concentrate at the finishing stage is the plasma method[4].The pre-enriched quartz particles(with standard particle size distribution 0.1-0.4 mm and total mineral impurities 100-120 ppm[4])are subjected into a plasma(～5-10 kK)stream and dynamic heated(resident time 10?3-10?2s)to temperature below their melting point.As a result of a series of physical-chemical mechanisms(plasma chemical desorption,thermal destruction and evaporation of low-melting impurities from the particle surfaces),the mineral impurities and gas-liquid inclusions[5]could be effectively removed from the solid quartz concentrate.After the following chemical etching,ultrasonic washing,dewatering and drying,a HPQ concentrate satisfied the IOTA-STD standard[2](industry standard for grading high quality fused quartz products)could be obtained.

The experimental results[4,6]showed that the total mineral impurities in quartz concentrate could be reduced by almost 5-10 times from 100-120 ppm to 10-20 ppm by using the electric arc torch as a plasma generator within power up to 20 kW.However,the arc materials are always found in the HPQ concentrate and limit its final purity level.For the purpose of minimizing the total element impurities in HPQ concentrate,it is necessary to use the electrodeless radio frequency inductively coupled plasma(RF-ICP)torch,which has been actively applied for thermal processing(heating,melting and evaporation)of ultra-pure materials[7-10].Until now the information about the enrichment efficiency(efficiency of removing mineral impurities and gas-liquid inclusion)of quartz concentrate in plasma jet generated by RF-ICP torch is almost absent.

Practically,it is difficult to theoretically evaluate the enrichment efficiency of quartz concentrate,which depends on a variety of physical-chemical interaction mechanisms.The results in[6]showed that the high enrichment efficiency of quartz concentrate is always accompanied by a high thermal destruction degree-the presence of cracks in particles and the split of large particles into smaller one.As a result,the excess of the thermal stress in particles(due to non-uniform particle temperature field)above the ultimate destruction strength could be considered as a comprehensive criterion for evaluating the thermal destruction degree and enrichment efficiency of quartz concentrate.

In order to determine the influence of the operating conditions of RF-ICP torch system on the thermal destruction degree and enrichment efficiency of quartz concentrate,a wide range of numerical studies about the spatial-temporal distributions of temperature and the resulting thermal stress in quartz particles should be made.In many previous works[11-14],the analysis of the spatial-temporal distributions of temperature in particle was carried out only under constant plasma temperature.Furthermore,spatial-temporal distributions of thermal stress in particles and their thermal destruction conditions have not been studied in those works.In[15],the temperature and thermal stress fields in quartz particles have been determined under a given time-dependent temperature on their surface.The influence of working parameters of RF-ICP torch and polydisperse particle flow on the dynamic heating process and thermal destruction conditions of quartz particles has not been considered.

In the present work,the main aims are to determine the operating conditions of RF-ICP torch system to guarantee the thermal destruction of all quartz particles(dp=0.1-0.4 mm)without overheating above their melting point.The numerical simulation of the turbulent mixing process of cool polydisperse particle flow with Ar and Ar-H2plasma generated by RF-ICP torch has been made.An approximate two-stage approach is proposed to calculate the spatial-temporal distributions of temperature and resulting thermal stress in quartz particles under dynamic heating in plasma flow.The influence of hydrogen volume fraction,particle feed rate,particle diameter distributions and injection conditions during thermal destruction conditions of quartz concentrate in RF-ICP torch system has been determined.

2.Physical and mathematical model

The accurate calculation of the spatial-temporal distributions of temperature and resulting thermal stress in quartz particles under dynamic heating in plasma flow is extremely difficult.In the present work under relative small Biot numbers(Bi≤0.05-0.5),an approximate two-stage approach is proposed.At the first stage,the calculation of the turbulent mixing process of polydisperse particle flow with plasma is carried out under the assumption of uniform temperature distribution in particle[16].At the second stage,the results about the time-dependent particle average temperature are applied to particle surface as a boundary condition for the calculation of spatial-temporal distributions of temperature and thermal stress.The accuracy of the two-stage approach would be evaluated in part 3.2.1.

2.1.Geometric and operating conditions of RF-ICP torch system

The RF-ICP torch system includes a PL-50 plasma torch and mixing chamber(figure 1).The axis of RF-ICP torch system orientates vertically.The basic dimension parameters of RFICP torch system have been given in table 1.The RF-ICP torch with three coils(figure 1,Position 6)works at a coupled power P=6.8 kW and generator frequency f=3 MHz.The plasma Q2=8 slpm and sheath Q3=90 slpm gases are axially supplied into the RF-ICP torch(figure 1,Position 2 and Position 3).The carrier gas with flow rate Q1=100-360 slpm is supplied through an annular channel into the mixing chamber(figure 1,Position 1).The plasma gas is Ar,while the carrier and sheath gases are Ar-H2mixtures within a variation of hydrogen volume fraction φ from 0 to 5%.

The quartz particles with diameter dp=0.1-0.4 mm and mass flow rateare introduced into the mixing chamber by the carrier gas.During the turbulent mixing process of cold polydisperse particle flow with plasma jet from RF-ICP torch,the particles are dynamic heated to temperature below their melting point.After that,they would be transported to a collector(figure 1,position 5)located at z=1400 mm from the exit of RF-ICP torch.

Table 1.Dimension parameters of RF-ICP torch system.

2.2.Magneto-hydrodynamic model

At the first stage,the processes of gas discharge in RF-ICP torch,turbulent mixing of plasma with polydisperse particle flow and particle dynamic heating under uniform internal temperature field are studied.The system of equations at this stage included Maxwell’s equations; gas dynamic equations and equations of particle motion and heating.

In the study of gas discharge and turbulent mixing processes in RF-ICP torch system under atmosphere pressure,the plasma is in local thermodynamic equilibrium(LTE)[17].

The thermal plasma is considered as optical thin.The detailed discussions about the validity of the assumption of optically thin plasma have been systematically discussed in[18].It is found that under atmospheric pressure,the effect of reabsorption of radiation in the plasma on the energy balance could be neglected when the plasma temperature T＜15 kK.In this situation the plasma could be considered as optically thin,the energy balance in the plasma would be determined by ohmic heating,heat conduction and optically thin radiation.

The spiral inductor coil is assumed as three parallel axisymmetric turns[19]and the velocity of working gases at inlets is azimuthally symmetric,the Maxwell’s and gas dynamic equations are two-dimensional in cylindrical coordinates.

For the particles,their melting and evaporation processes are not considered.The interactions between particles are neglected underwhen the particle-laden flow could be considered as dilute flow[20].The gas-particle interaction is considered and determined by the particle-source-in-cell(PSI-cell)method[21].

The Maxwell’s equations are written as in[22]under the assumption of quasi-stationary approximation.Taking into account of the electromagnetic forces,Joule heat,radiation loss and gas-particle interaction,the magneto-hydrodynamic equations for the subsonic multicomponent polydisperse flow could be written as follows[23]:

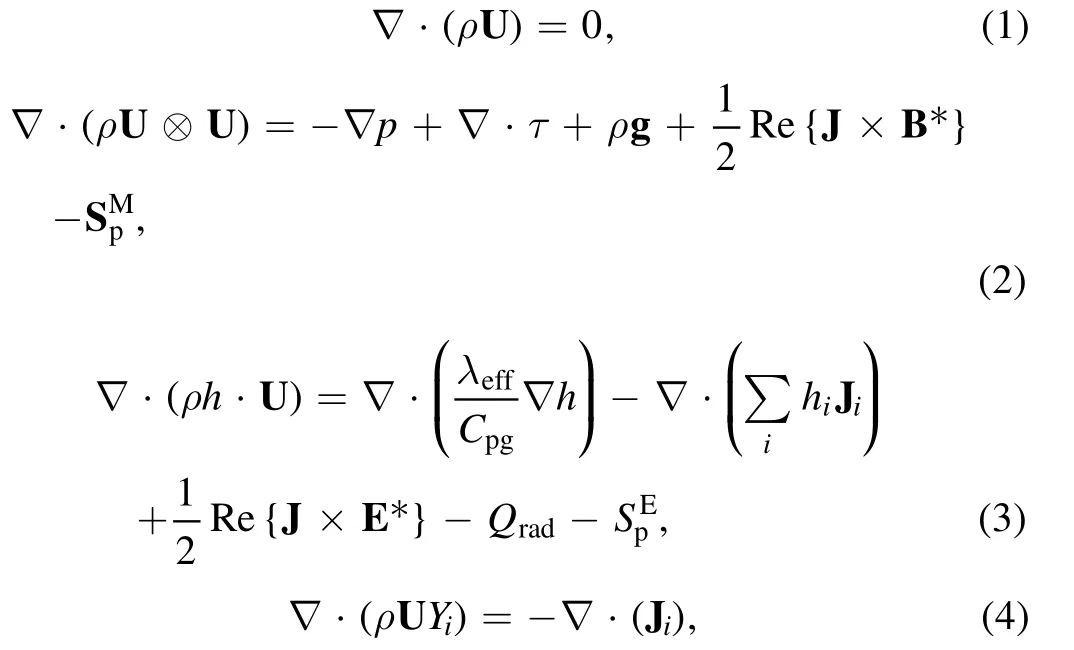
For optically thin plasma,the volumetric radiation lossQradin equation(3)could be calculated as:

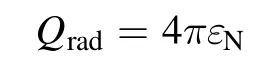
where the net emission coefficientεNis a function of temperature,pressure and gas compositions[25].

hi,Yiand[24]are the specific enthalpy,mass fraction and diffusion current of i-th gas(Ar or H2gas).andare the combined ordinary and turbulent diffusion coefficients for the i-th gas.

For a binary mixture composed by the gases i and j,the combined ordinary diffusion coefficientcould be calculated as[26-28]:,wherenandρare the gas number density and mass density,andare the average masses of the heavy species of the respective i and j gases,is the combined diffusion coefficient due to mole fraction gradients.The dependences ofon the gas temperature and compositions for Ar-H2binary mixtures could be found in[29].It should be noted that in the present work the diffusion due to temperature gradients has been reasonably neglected[30].

The contributions of particle momentumand enthalpysources to the gas phase(plasma-particle interactions)in equations(2)and(3)are determined by the PSI-cell method[21].In a given cell(i,j)the values of and could be calculated as follows[23]:

The turbulent effects in the mixing chamber have been considered in the flow calculations using a standard k-ε model[31]:

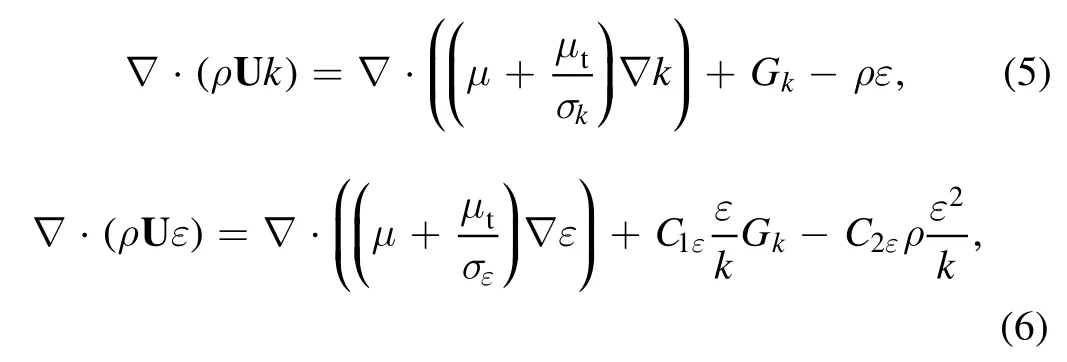
During the dynamic heating of quartz particle in plasma flow,their melting and evaporation processes are neglected.The quartz particle is considered as spherical and the temperature in it is uniform.Under those assumptions the motion and heating process of a single quartz particle in the plasma could be described as follows[23]:

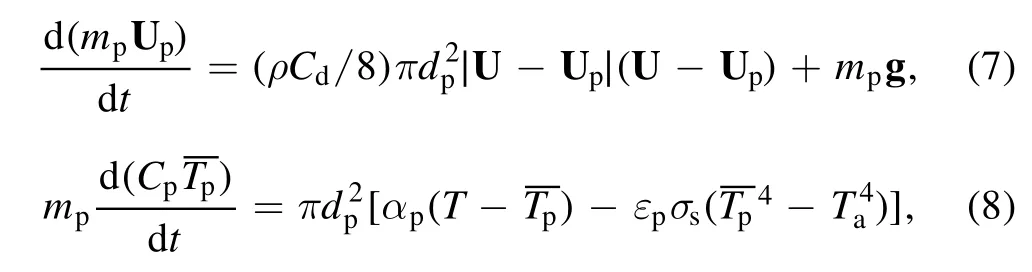
whereCpandεpare the specific heat capacity and surface emissivity of quartz particle.andRep=ρdp∣U?Up∣μare the Stoke coefficient and Reynolds number for the sphere[33].Upis the vector of particle velocity.The heat transfer coefficient between gas and particleαpcould be determined by the Ranz-Marshall correlation:σsis the Stefan-Boltzmann constant.Tais the room temperature(300 K).

The boundary conditions for equations(1)-(6)are given as follows:the gases velocities at all the walls are zero.The temperature on the external surface of plasma confinement tube and inner surface of mixing chamber is equal to 300 K.At the inlets(z=0)of RF-ICP torch and outlet of annular channel(z=Z2),the velocities of plasma U2=sheathand carrier gases U1=Q1/(2πR2δ3sinθ).The working gas temperature at the inlets of RF-ICP torch and outlet of annular channel is constant T=300 K.At the exit of the mixing chamber(z=Z3)the pressurep=patm=105Pa.

The quartz particles dp=0.1-0.4 mm are uniformly introduced into mixing chamber through an annular channel by the carrier gas.The particle injection angle(inclination angle of annular channel with respect to r-coordinate)varies in the range of θ=20°-80°.The injection velocity of quartz particle at the exit of annular channel Up=U1·Kp,where the correction coefficient Kp[34]is set at 0.8,0.6,0.5 and 0.4 for quartz particles of diameter dp=0.1,0.2,0.3 and 0.4 mm,respectively[35].

Three different particle diameter(dp=0.1-0.4 mm)distributions are considered:1-uniform in diameter by mass;2-uniform in diameter by number; 3-Rosin-Rammler distribution within parameters de=0.2 mm and γ=3[36].In the following studies the particle diameter distribution is described by the first function except in section 3.3.1.

At constant pressure the density,specific heat capacity,viscosity,thermal and electric conductivities of the mixtures are all temperature and composition dependent quantities,those thermophysical properties could be obtained from[37].

System of equations(1)-(8)is solved based on the finite volume method.The numerical simulations are made in ANSYS CFX.17.2.The meshes in the calculating zones are built in ANSYS MESH with 156250 hexahedral cells in the plasma region and walls,and a total of 7489 non-structural tetrahedral cells in the coils and the free space regions.

2.3.Model of strain-stress in particle under dynamic heating

At the second stage,the analysis of the spatial-temporal distributions of temperature and strain-stress in a spherical particle under dynamic heating is made by solving the Fourier-Kirchhoff equation and the equilibrium equation written by the vector of relative displacementu=u(r,t)[38]:

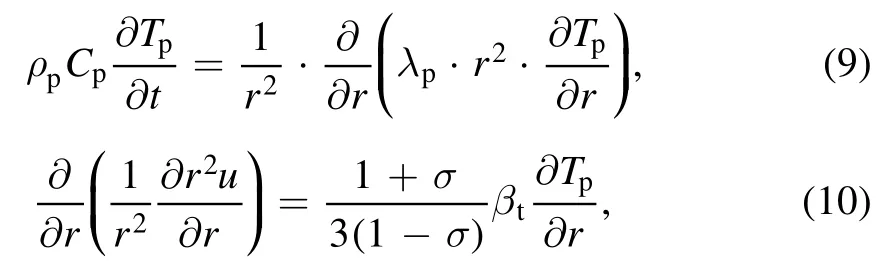
whereρp,λp,βtandσare the density,thermal conductivity,coefficient of volume expansion and Poisson’s ratio of quartz material.Tp=Tp(r,t)is the spatial-temporal distribution of temperature in the particle.Under the assumption of spherical symmetry,the strain uikand stress σiktensors have only diagonal components and could be calculated as follows[38]:

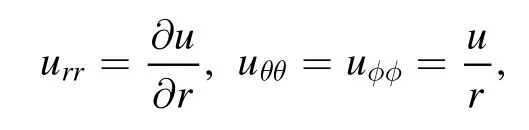
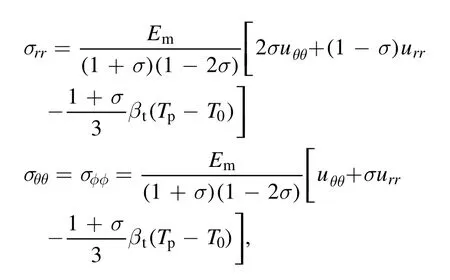
where T0=300 K is the initial particle temperature.Emis the modulus of elasticity.

The mechanical properties of quartz material are given in[39]:σ=0,12,Em=90.5 GPa,σt=50 MPa,σc=1.1 GPa.Since the tensile strength σtof quartz material is much smaller than its compressive stress σc,the criterion for destructing particle is considered as the excess of equivalent thermal stress σequabove the tensile strengthσequ≥σt.The value of σequis determined by the Mohr-Coulomb theory[40]:σequ=σ1?ψσ3.Here ψ=σt/σc,σ1=max(σrr,σθθ)andσ3=min(σrr,σθθ).The thermophysical parameters of quartz material are obtained from[41,42].Their dependences on the temperature show a non-linear characteristic at the phase transition point(from α to β phase)Tp=Tαβ≈847 K[42].

Under the assumption of spherical symmetry the calculation region is 1/8 spherical particle[15].A symmetry boundary condition is set on the three axial cross sections.The dependences of particle average temperature on timeTp(t)obtained at the first stage are applied on the particle surface:Ts(t)=Tp(r=dp2,t)=Tp(t).The value of displacement on the particle surface(r=dp/2)is zero.

The numerical solutions of equations(9)and(10)are carried out in ANSYS Mechanical APDL by the finite element method.The element type in the calculation region is quadratic 20-node,the solid90 and solid186 are applied for calculating the temperature and thermal stress distributions,respectively.The total number of elements in the small particles dp=0.1 mm is N=13500,while in the large particles dp=0.4 mm,N=23328.

3.Results and discussion

3.1.Temperature and velocity fields in RF-ICP torch system

3.1.1.Comparison of plasma temperature distributions with experimental results.We first validate the present CFD simulation with the geometries and parameters covered in[31].The numerical solution of system of equations(1)-(4)is carried out without a supply of annular polydisperse particle flow.

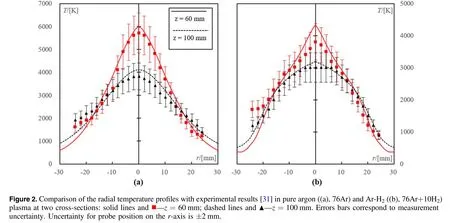
The PL-35 torch with a coupled power P=9 kW and generator frequency ω=13.56 MHz operates at 60 kPa.The inner diameters of the plasma confinment tube and mixing chamber are 35 mm and 325 mm,respectively.The flow rates are 4 slpm of Ar for the carrier gas through the central injection probe,12 slpm of Ar for the plasma gas and a mixture made of 60 slpm of Ar and a variable amount of H2(0 or 10 slpm)for the sheath gas.The radial profiles of plasma temperature in the mixing chamber at two different crosssections z=60 mm and z=100 mm from the exit of PL-35 torch have been calculated and compared with experiments.

As can be seen from figure 2 that with the addition of hydrogen(10 slpm H2)into the RF-ICP torch system of argon plasma,the plasma temperature around axis at the same crosssections significantly decreases(in 1000-2000 K)as a result of the higher specific enthalpy of hydrogen[43].In the argon plasma the numerical results about the radial temperature profiles at those two different cross-sections are well in agreement with the experiments.The maximum relative difference of plasma temperature ΔTmaxis small of about 5%(figure 2(a)).In the Ar-H2plasma(with 10 slpm of H2)at the cross-section z=100 mm ΔTmaxis also relative small,while at z=60 mm it is relative high of about 20%(figure 2(b)).As a whole,the 2D standard k-ε model could satisfactorily predict the temperature field in the expanded mixing chamber,where the turbulent effect substantially increases and should be considered.

The relative large difference between experiments and 2D numerical results at z=60 mm for Ar-H2plasma may be due to the measurement bar errors and 3D effect of RF-ICP torch.First,in the experiments the radial temperature profiles are obtained by a commercial enthalpy probe(Tekna model EN476).The higher the plasma temperature,the higher the measurement uncertainty would be along the vertical T-axis.Second,for measuring the radial temperture profiles the mounted enthalpy bulkhead with probe moves on a rail,allowing a displacement along the r-axis within an uncertainty of±2 mm[28].Third,the induced unbalanced Lorentz forces in the discharge may result in non-axisymmetric thermo-fluid-dynamic fields.Therefore,the assumption of 2D model may lead to some deviation of the temperature field from experiment.Besides that,the non-axisymmetric outlet at the bottom of the mixing chamber has also not been considered in the 2D model.The recirculation flow arose due to the non-axisymmetric outlet could also lead to a deviation of the experimental results from the 2D model.

It should be noted that due to the different geometric structure and dimensions(tube inner diameter,turn numbers of inductor coil and etc),the PL-35[31]and PL-50(in present work)torches usually work under different coupled powers,generator frequencies and gas flow rates.However,the free plasma jets from the exit of PL-35 and PL-50 torches are considered to have a similar flow regime and gas dynamic and thermal fields[44].Since the plasma gas flows in the channel of both RF-ICP torches have a close value of average and maximum Reynold numbers[45],as well as a close value of maximum axial gas velocity and temperature.Consequently,the coincidence of radial temperature profile obtained by numerical calculation and experiments in the mixing chamber of PL-35 torch indicates that,the standard k-ε model could also been used for predicting the gas dynamic and thermal fields for PL-50 torch system.

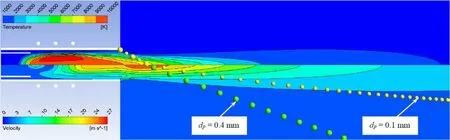
Figure 3.Temperature and velocity fields and particles trajectories in the RF-ICP torch system of Ar plasma under Q1=180 slpm,θ=60°andGSiO2=1×10?4 kg s?1.

3.1.2.Turbulent mix process of polydisperse particle flow with plasma jet.As the thermal plasma jet exits the RF-ICP torch,it encounters a cross polydisperse particle flow at its outer edge.The large velocity difference causes rolling up of the shear layer flow into a ring vortex.This formed vortex rings at the outer edge of the plasma jet would coalesce,entangle with adjacent rings and break down into large-scale eddies of cold gas[46].After that,the large-scale eddies of cold gas would diffuse axially toward the plasma centre and encounter with the eddies of high temperature gas.Due to the relative high difference of density(or inertia)and velocity,the eddies of cold gas and high temperature gas would collide with each other and break down into smaller and smaller eddies.Eventually,the diffusion and turbulent mixing processes reach the centreline of the plasma jet.After the fully turbulent mixing the temperature of plasma jet substantially decreases.The cooling effect not only depends on the momentum flux ratio of the cross flow to the plasma jet[47,48],but also the feed rate of quartz particles[23].In the present work under Q1=180 slpm,θ=60°,Q2+Q3=98 slpm andGSiO2=1×10?4kg s?1,the temperature of plasma jet could decrease to 400 K at Z3≥1600 mm.

During the turbulent mixing process of polydisperse particle flow with plasma jet,the quartz particles are injected into the central region(figure 3).At the moment tp≈5×10?3-2×10?2s when the quartz particles pass through axis,they are heated to the maximum.The quartz particle trajectories could be substantially different.The large particles dp=0.2-0.4 mm almost fly by straight lines due to the high inertia.While small particles,dp=0.1-0.15 mm,are more sensitive to the central plasma jet,their trajectories could bend toward the axis and involved into the high temperature zone.Therefore,the small particles would be exposed to higher gas temperature and may be overheated above their melting point.Note that compared with traditional axial injection of particles,the radial injection of particles through the annular channel after the discharge zone could better quench the thermal plasma jet,as well as rapidly transport the quartz particles throughout the central high temperature zone without melting.

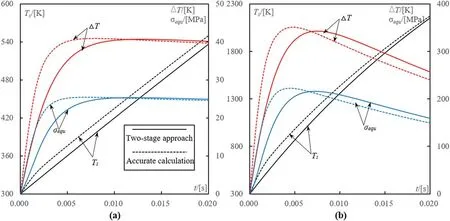
Figure 4.Changes of particle(dp=0.4 mm)surface temperature Ts,temperature difference ΔT between its surface and center and equivalent thermal stress in its center σequ with time under different Biot numbers(Bi=0.04,(a))and(Bi=0.4,(b)).

3.2.Thermal stress in particles under dynamic heating

3.2.1.Evaluation of accuracy of two-stage approach.In order to evaluate the accuracy of using an approximate two-stage approach,the spatial-temporal distributions of temperature and equivalent thermal stress in large particle(dp=0.4 mm)have been calculated and compared with accurate numerical solution under a simplified test condition.

In the tests,the particle is heated in stationary plasma(Nu=2)under a given gas temperatureTg=4500 K and coefficient of heat transferαp.The gas temperatureTg=4500 K is taken in according to the average gas temperature in mixing region under dense loading conditions.The values ofαpand Biot numberBi≈Nuλgλpare set in according to the working gas compositions:in Ar gas-Bi≈0.04 and in Ar-H2(φ=5%)mixtures-Bi≈0.4[11].Furthermore,the thermophysical(λpandCp)and mechanical properties(βt)of quartz material are also considered constant in the test.

By using the two-stage approach,the temperature fieldTp1(r,t)in particle is calculated as follows:at the first stage the particle average temperatureis determined under the assumption of uniform temperature distribution[49].At the second stage the value ofwould be applied on the particle surface as a boundary condition for solving equation(9)and establishing the spatial-temporal distributions of temperatureTp1(r,t)in the particle.In the direct numerical solution the spatial-temporal distributions of temperature in the particleTp2(r,t)are obtained by solving equation(9)under convection boundary condition.

The results about the temperature fieldTpk(r,t)calculated by the two-stage approach and direct numerical solution under two different Biot numbers are represented by the particle surface temperatureTsk(t)=Tpk(r=dp2,t)and the temperature difference between their surface and centerΔTk(t)=Tpk(r=dp2,t)?Tpk(r=0,t)(k=1,2)(figure 4).As can be seen that by using two-stage approach,the particle surface temperature could be 3%-5%and 13%-17% underestimated than that by direct numerical solution under Bi=0.04 and 0.4,respectively.The maximum changes inΔTk(t)are found at the initial interval of time 0＜t＜0.005 s,they are about 10%-15% underBi=0.04 and 25%-30% under Bi=0.4.Therefore,under relative high Biot number(in Ar-H2mixtures with φ=5%),the differences inTsk(t)andΔTk(t)obtained by those twoσequ(t)has been calculated under two spatial-temporal different methods could be 2-4 times higher than that under small Biot number(in Ar gas).

For the purpose of evaluating the influence of different temperature fields on the thermal destruction conditions of quartz particle,the equivalent thermal stress in particle center distributions of temperatureTp1(r,t)andThe changes ofσequ,k(t)(corresponding toTpk(r,t),k=1,2)with time under Bi=0.04 and Bi=0.4 have also been shown in figure 4.As can be seen that the difference ofσequ,k(t)at the initial interval 0＜t＜0.005 s could be as high as that ofΔT(t).

kHowever,the maximum equivalent thermal stress in the particle centeris found almost coincidence with each otherin both cases(Bi=0.04 and 0.4).In the present work the value ofis considered as a critical parameter for estimating the thermal destruction conditions of quartz material.Consequently,the application of the two-stage approach for determining the thermal destruction conditions of particles in plasma flow is approximately valid under φ≤5%.

3.2.2.Particle dynamic heating in Ar plasma.During the dynamic heating process of quartz particles in polydisperse plasma flow,the maximum temperature and equivalent thermal stress are found on the particle surface and in their center,respectively.Therefore,in the following parts the discussions about the thermal destruction conditions of quartz particles would be performed based on the changes of particle surface temperatureTs(r=dp2,t)and central equivalent thermal stressσequ(r=0,t)on the time.

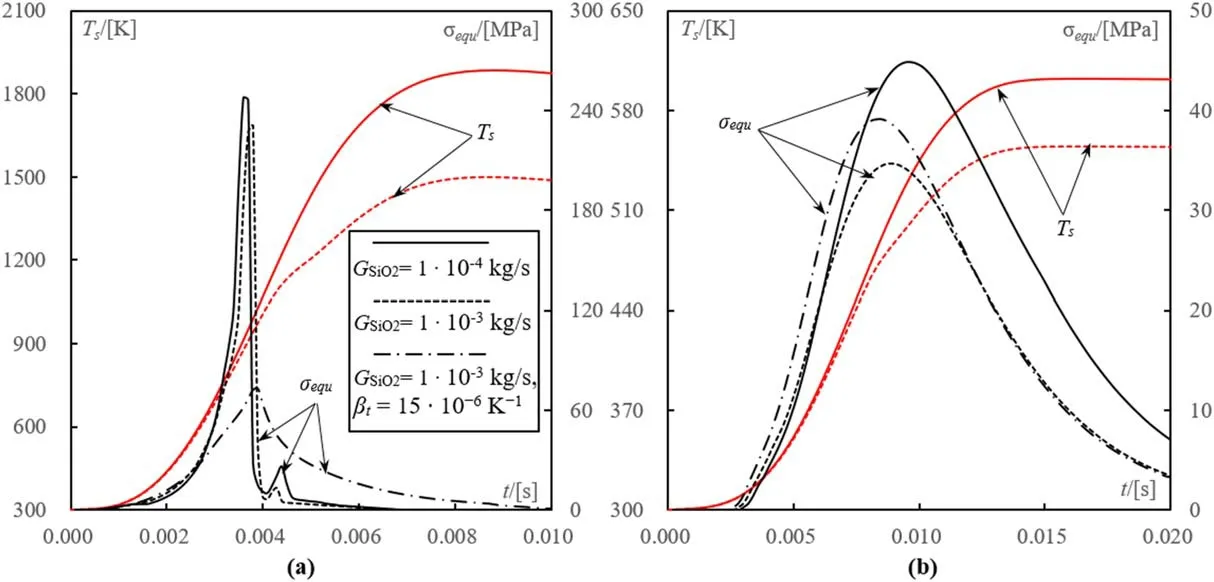
Figure 5.Changes of small(dp=0.1 mm,(a))and large(dp=0.4 mm,(b))particle surface temperature Ts and equivalent thermal stress σequ in their center with time in pure argon plasma under Q1=180 slpm and θ=60°.

The numerical simulations are carried out under a given flow rate of carrier gas Q1=180 slpm and injection angle θ=60°.It is found that under relative low feed rate1×10?4kg s?1,the small quartz particles dp=0.1 mm would be overheated above their melting point(Tm≈1850-1900 K).The equivalent thermal stressσequin small particles reaches to its maximumaround the phase transition point Tp=Tαβ≈847 K.The value ofin small particles is almost five times higher than the tensile strength(σt=50 MPa)(figure 5(a)).With increasing the feed rate to,their maximum surface temperature decreases to 1570 K due to the loading effect.

However,even under relative small feed rate1×10?4kg s?1,the maximum temperature on large particle(dp=0.4 mm)surface could only reach to 600 K.The maximum equivalent thermal stress in large particles is smaller than the tensile strength(figure 5(b)).As a result,it is difficult to guarantee the thermal destruction of all quartz particles(dp=0.1-0.4 mm)without overheating the smallest one in the RF-ICP torch system of Ar plasma.

3.2.3.Particle dynamic heating in Ar-H2plasma.In order to intensify heat exchange from plasma to particles and arose sufficient thermal stressin particles,the Ar-H2mixtures are applied as the working gases due to their higher thermal conductivity.The hydrogen volume fraction φ in Ar-H2mixtures varies from 0 to 5%.The flow rate of carrier gas and particle injection angle are set at Q1=180 slpm and θ=60°,respectively.

As can be seen in Ar-H2plasma under a given feed ratethe maximum particle temperature and its increasing ratio rise up in 1.5-2 times with an increase of φ from 0 to 5%(figure 6).The maximum equivalent thermal stressin large(dp=0.4 mm)particles rises up from 34 to 96 MPa and exceeds the tensile strength(figure 6(b)).However,the maximum temperature on small particle(dp=0.1 mm)surface would exceed the melting pointwith the addition of hydrogen into argon plasma(φ=5%).

Since the dependences of small(dp=0.1 mm)and large(dp=0.4 mm)particle surface temperature on the feed rate(loading effect)are substantially different,the aim of destructing all quartz particles without overheating could be realized by varyingBy increasing the value offrom 1×10?3to 8×10?3kg s?1,the maximum temperatureon small particle surface significantly decreases from 2400 K to 1400 K(below the melting point).While the changes ofon large particle surface are relative small and the value ofin their centre is still higher than the tensile strength.

As a result,there should be a minimum feed rate,under which all the quartz particles could be destructed without overheating the smallest oneA further increase of particle feed rate fromto a(maximum feed rate)would result in a decrease of the maximum equivalent thermal stressin large particles to tensile strength

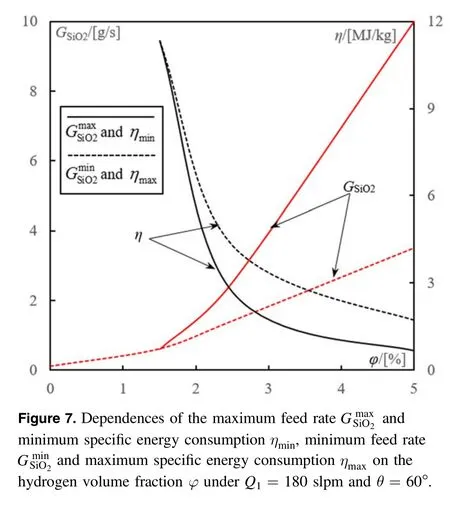
The specific energy consumption for particle heating is defined as the amount of thermal energy per unit mass of quartz particle:Corresponding to the minimum and maximum feed rates,the dependences of the maximumηmaxand minimumηminspecific energy consumptions on hydrogen volume fraction have also been shown in figure 7.Under a given coupled power P=6.8 kW,the increase of hydrogen volume fraction from φ=φcr=1.5%- 2% to 5%leads to a significant decrease ofηminandηmaxfrom 10 MJ kg?1to 0.68 MJ kg?1and 1.71 MJ kg?1,respectively.

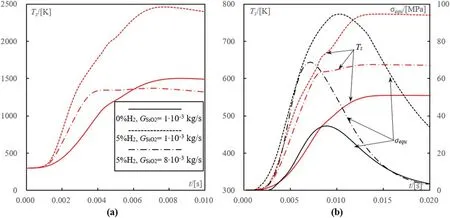
Figure 6.Changes of small(dp=0.1 mm,(a))and large(dp=0.4 mm,(b))particle surface temperature Ts and equivalent thermal stress σequ in large particle center(b)with time under Q1=180 slpm and θ=60°.

3.3.Effects of particle diameter distributions and injection conditions

The effects of particle diameter distributions,injection angle and flow rate of carrier gas on their thermal destruction conditions are determined in Ar-H2plasma under a constant hydrogen volume fraction φ=5%.

3.3.1.Effect of particle diameter distributions.In practice,the particle diameter distributions could be substantially different,depending on their deposits and processing technologies[50].Therefore,it is essential to investigate the effect of particle diameter distribution on their thermal destruction conditions.In this section,three different particle diameter distributions have been studied:uniform in diameter by mass,uniform in diameter by number and Rosin-Rammler distribution with mean diameter de=0.2 mm and spread parameter γ=3[36].The flow rate of carrier gas and injection angle from the annulus channel are constant at Q1=180 slpm and θ=60°.

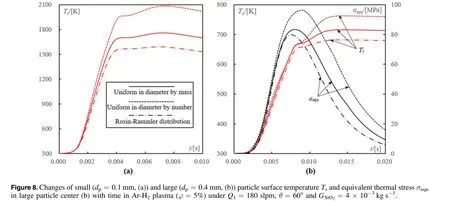
Under the uniform distribution in particle diameter by number,the mass fraction of particles with diameter dp≥0.3 mm would be around 80% of all particles.The loading effect of polydiperse particle flow would be relative small in the mixing chamber.This leads to an increase of the maximum temperature and equivalent thermal stress in particles.As a result,the value ofrises up and the processing ability of RF-ICP torch system becomes greater(figure 8(b)).Note that in this case,more particle feed rate is also needed to prevent the overheating of small particles(figure 8(a)).Under a given hydrogen volume fraction φ=5%,the minimum and maximum quartz feed rates rise up from 3.5×10?3to 5.5×10?3kg s?1and from 1×10?2to 1.2×10?2kg s?1,respectively.

In contrast,when the particle diameter distribution changes from uniform distribution by mass to Rosin-Rammler distribution(de=0.2 mm and γ=3),the mass fraction of large particles with diameter dp≥0.2 mm would decrease from 50% to 30%.The loading effect of polydisperse particle flow becomes more pronounced,the minimum and maximum quartz feed rates are found to decrease from 3.5×10?3to 2.5×10?3kg s?1and from 1×10?2to 8×10?3kg s?1,respectively.

As a result,the less proportions of large particles,the higher the loading effect of polydisperse particle flow and the lower the processing ability of RF-ICP torch system.Among those three different particle diameter distributions,the value ofreaches to its maximum under uniform distribution by number and minimum under the Rosin-Rammler distribution.It should be noted that the discussions about the influence of particle diameter distributions on the process ability of RF-ICP torch system provide useful information for choosing the raw quartz material.3.3.2.Effects of injection angle and flow rate of carrier gas.In this part the effects of particle injection angle θ(inclination angle of annular channel)and flow rate of carrier gas Q1on the thermal destruction conditions of quartz particles in Ar-H2plasma(φ=5%)have been studied.The values of θ and Q1vary in the range from 20°to 80°and from 100 to 360 slpm,respectively.The particle feed rate is fixed at=4×10?3kg s?1.

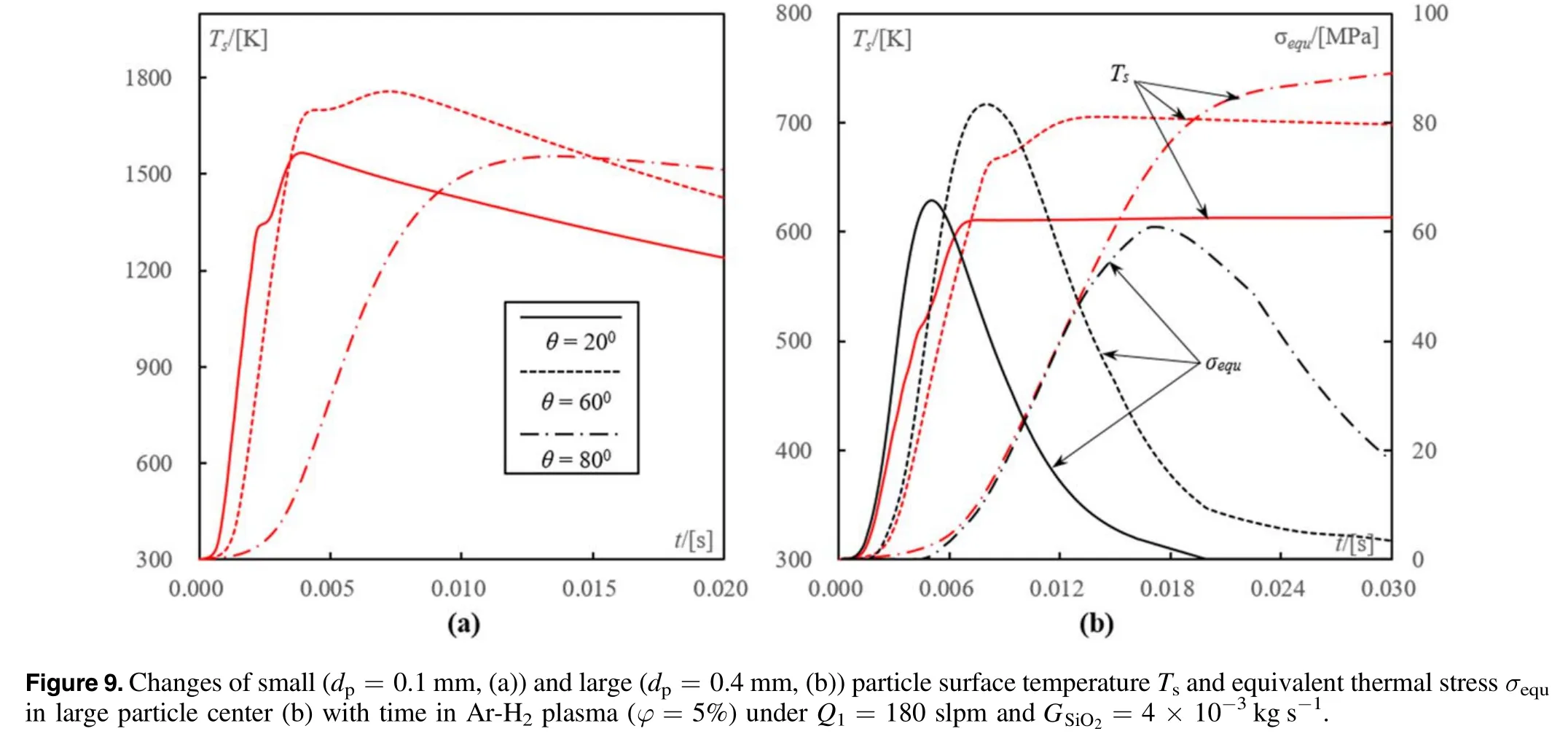
Figure 9 shows the changes of particle temperature and equivalent thermal stress with time under Q1=180 slpm and different injection angles θ.The effect of injection angle θ on the maximum equivalent thermal stress in particlesshows a non-monotonic characteristic.With the decrease of θ from 80° to 60°,the heat exchange between plasma and particles becomes greater and the particle temperature could reach to its maximum under a relative small interval of time(figure 9(b)).A higher temperature gradient could form in particles and the value ofin them monotonically rises up.

However,in the range of relative small injection angle(θ=20°-60°)the maximum equivalent thermal stressin large particle reduces with the decrease of θ.As the injection direction of annular channel becomes more perpendicular to axis,the particle resident time in high temperature region significantly reduces and the particle maximum temperature becomes smaller.The value ofin large particles(dp=0.4 mm)decreases to the tensile strength under

It is found that there is an optimal injection angleθopt≈50°-60°,under which the value ofin particles is highest.This could be explained as that,under relative high injection angles the particle internal temperature gradient would decrease,while under relative small injection angles the particle resident time in high temperature region as well as the particle maximum temperature would reduce

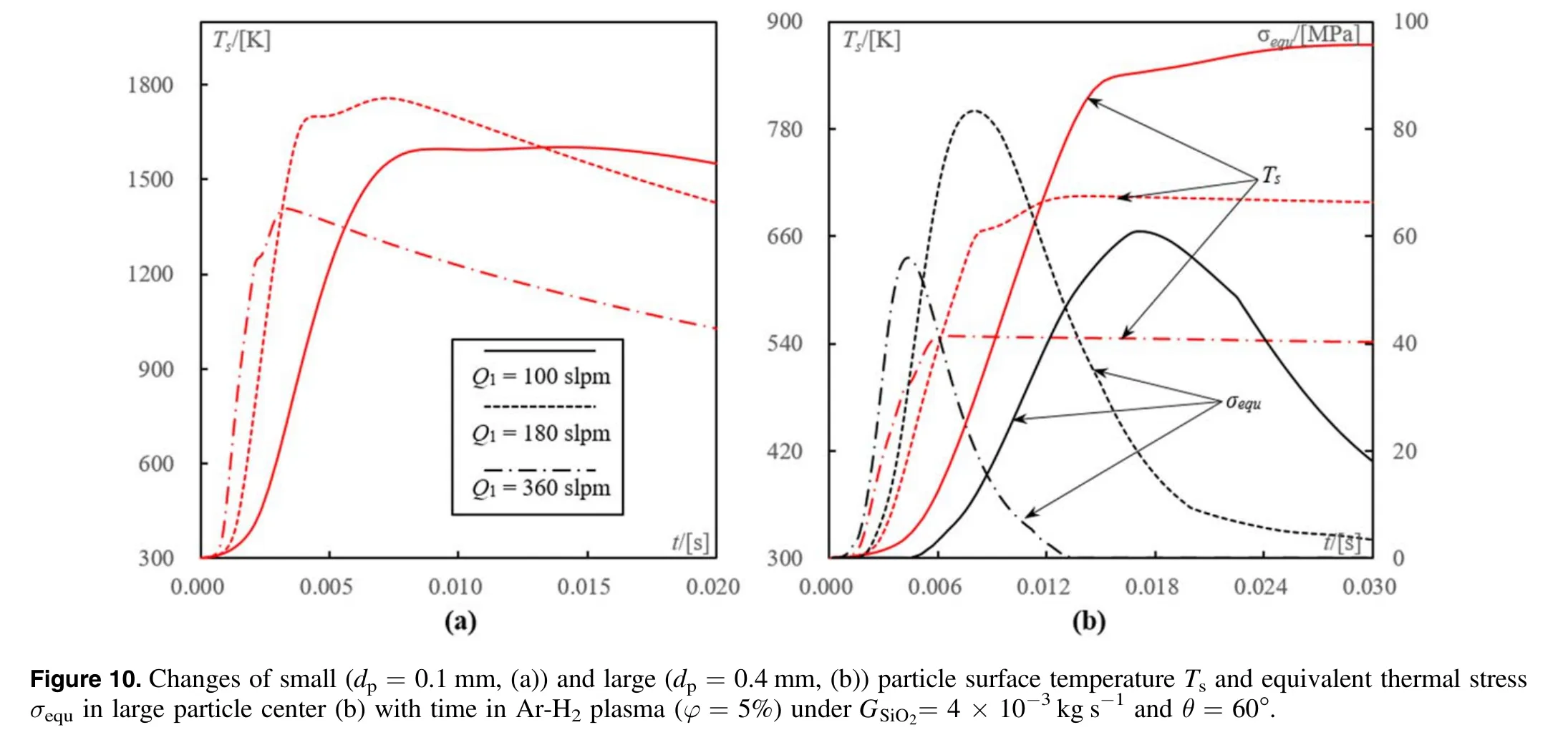
The effect of the flow rate of carrier gas Q1on the value ofalso shows a non-monotonic characteristic.When Q1decreases from 180 to 100 slpm,the value ofin the large particles(dp=0.4 mm)substantial reduces to 60 MPa(figure 10).The particle flight time from the exit of annular channel to axis becomes longer,the large particle temperature reaches to its maximum only at t≈0.02 s when Q1=100 slpm.This makes it difficult to establish sufficient temperature gradient and arouse high thermal stress in particles to ensure their thermal destruction.

In contrast,under very high flow rate of carrier gas Q1=360 slpm,the high temperature gas flow in the central region would be effectively quenched.The maximum temperature and equivalent thermal stress in large particles reduce to 550 K and 52 MPa,respectively.The numerical calculations show that the optimal flow rate of carrier gas Q1,optis around 160-220 slpm when θ=60°.

It is interesting to find that,under the deviation of the injection conditions from the optimal points(θoptand Q1,opt),the maximum surface temperature of small(dp=0.1 mm)particles monotonically decreases(figures 9(a),10(a)).This indicates that both the values ofandwould reduce under the deviation of the injection conditions from the optimal points.

4.Conclusion

The numerical simulations of turbulent mixing process of polydisperse quartz particle flow with Ar and Ar-H2plasma jet generated by RF-ICP torch are made.The spatial-temporal distributions of temperature and thermal stress in the particles under dynamic heating in plasma are calculated by using an approximate two-stage approach.The thermal destruction conditions of quartz particles with diameter distribution in the range of dp=0.1-0.4 mm have been established.

The numerical results show that the application of RFICP torch system of Ar plasma is difficult for the thermal destruction of all the quartz particles.When the maximum equivalent thermal stress in large particles(dp=0.3-0.4 mm)becomes close to the tensile strength,the small particles dp=0.1-0.15 mm would be overheated above their melting point.

The addition of hydrogen into argon plasma intensifies the heat exchange from plasma to particle,making it possible to effectively improve the thermal destruction conditions of quartz concentrate.The maximum equivalent thermal stress in the large particles may be 1.5-2 times higher than the quartz tensile strength.The possible overheating(melting)process of small particle dp=0.1-0.15 mm in Ar-H2plasma could be avoided by modifying the gas compositions and particle feed rate.

It is found that the thermal destruction of all quartz particles in Ar-H2plasma could be realized,only when the hydrogen volume fraction φ in the mixtures is above a critical value(φ≥φcr≈1.5%-2%)and the particle feed rate in a certain rangeThe dependences of the maximumand minimumparticle feed rates,as well as their corresponding specific energy consumptions,on the hydrogen volume fraction in the range of φcr≤φ≤5%are established.With an increase of hydrogen volume fraction in gas mixtures,the maximum and minimum feed rates monotonically rise up.When φ=5% the ranges of particle feed rate and specific energy consumption are found at 3.5×10?3-1×10?2kg s?1and 0.68-1.71 MJ kg?1,respectively.

The effects of different particle diameter distributions,injection angle θ and flow rate of carrier gas Q1on the thermal destruction conditions of quartz concentrate have been determined.It is found that the higher the mass fraction of large particles,the lower the loading effect and the higher the values ofand.

The effect of particle injection angle and flow rate of carrier gas on the thermal destruction conditions shows a nonmonotonic characteristic.The optimal values of injection angle and flow rate are found aroundθopt=50°-60° and Q1,opt=160-220 slpm,under which there is a maximum value ofin the particles.