Laddawan AIEMSOMBOON Wutiphol SINTUNAVARAT

Department of Mathematics and Statistics, Faculty of Science and Technology,Thammasat University Rangsit Center, Pathumthani 12121, Thailand

E-mail: Laddawan Aiemsomboon@hotmail.com; wutiphol@mathstat.sci.tu.ac.th

Abstract In this work, we apply the Brzd?ek and Ciepli′nski’s fixed point theorem to investigate new stability results for the generalized Cauchy functional equation of the form where a,b ∈N and f is a mapping from a commutative group (G,+) to a 2-Banach space(Y, ). Our results are generalizations of main results of Brzd?ek and Ciepli′nski [J Brzd?ek,K Ciepli′nski. On a fixed point theorem in 2-normed spaces and some of its applications.Acta Mathematica Scientia, 2018, 38B(2): 377–390].

Key words Fixed point theorem; generalized Cauchy functional equation; 2-normed space;stability

1 Introduction and Preliminaries

Throughout this article, the pairs (G,+) and (Y,) denote a commutative group and a 2-normed space, respectively. Also, N stands for the set of all positive integers, N0:=N ∪{0},R+:=[0,∞), and BAdenotes the family of all functions from a set A into a set B.

In the mid 1960s,the concept of a 2-normed space and the theory of 2-normed spaces were first introduced by G¨ahler[10]. Next,G¨ahler[11]and White[20]studied the theory of 2-Banach space.

Definition 1.1Let X be a real vector space with dim X ≥2. A function:X×X →R+is called a 2-norm on X if it satisfies the following conditions for all x,y,z ∈X and α ∈R:

Example 1.2Let X =R2and:X ×X →R+be defined by

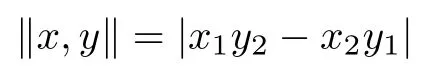
for all x=(x1,x2),y =(y1,y2)∈R2. Then,is a 2-norm on R2.

Example 1.3Let X =R3and:X ×X →R+be defined by

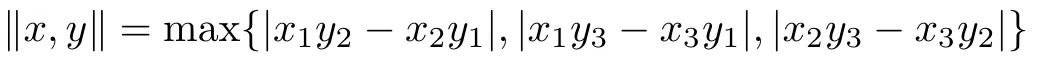
for all x=(x1,x2,x3),y =(y1,y2,y3)∈R3. Then,is a 2-norm on R3.

Definition 1.4A sequence {xn} in a 2-normed space (X,) is called a Cauchy sequence if there are linearly dependent y,z ∈X such that

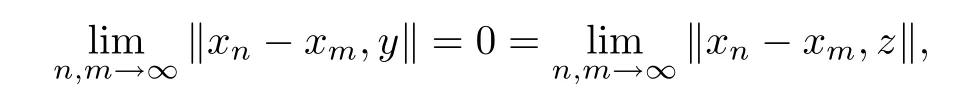
whereas {xn} is said to be convergent if there exists a point x ∈X (called a limit of this sequence and denoted bywithfor all y ∈X.

Definition 1.5A 2-normed space in which every Cauchy sequence is convergent is called a 2-Banach space.

The following lemma is derived from the fact that every convergent sequence has exactly one limit and properties of the limit.

Lemma 1.6([8]) Suppose that X is a 2-normed space. If x,y1,y2∈X,y1,y2are linearly independent and

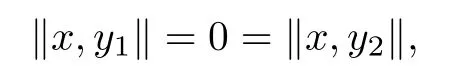
then x=0.

Lemma 1.7([8]) Suppose that X is a 2-normed space. If {xn} is a convergent sequence in X, then

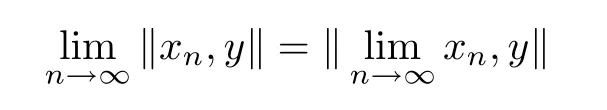
for all y ∈X.

On the other hand, the stability theory for functional equations was initiated by a question of Ulam [19] in 1940 as follows:

QuestionLet (G1,?) be a groups and (G2,?,d) be a metric group with a metric d :G2×G2→[0,∞). Given ? > 0, does there exist a δ > 0 such that if a function h : G1→G2satisfies the inequality

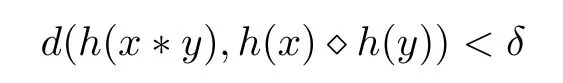
for all x,y ∈G1, then there is a homomorphism H :G1→G2with

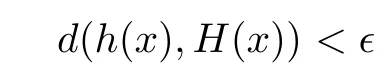
for all x ∈G1?

Afterward,Hyers[13]gave a partial answer to Ulam’s question and established the stability result as follows:

Theorem 1.8([13]) Let E1and E2be two Banach spaces and f :E1→E2be a function such that

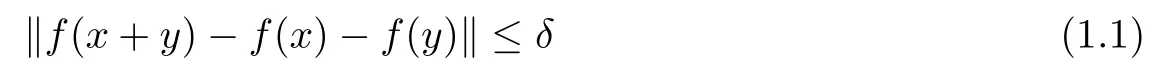
for some δ >0 and for all x,y ∈E1. Then, the limit

exists for each x ∈E1, and a mapping A : E1→E2defined by (1.2) is the unique additive function such that

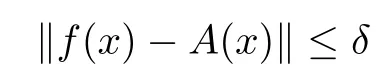
for all x ∈E1. Moreover, if f(tx) is continuous in t for each fixed x ∈E1, then the function A is linear.

In view of this result, the additive Cauchy equation f(x+y)=f(x)+f(y) is said to have the Ulam-Hyers stability on (E1,E2) if for each function f :E1→E2satisfying the inequality(1.1) for some δ > 0 and for all x,y ∈E1, there exists an additive function A : E1→E2such that f ?A is bounded on E1. Next, Aoki [4] and also independently Rassias [17] obtained the following theorem.

Theorem 1.9([17]) Let E1and E2be two Banach spaces and f :E1→E2be a function.If there is a real number p such that 0 ≤p<1 and f satisfies the following inequality

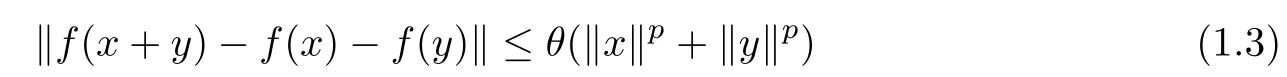
for some θ ≥0 and for all x,y ∈E1, then there exists a unique additive mapping A:E1→E2such that

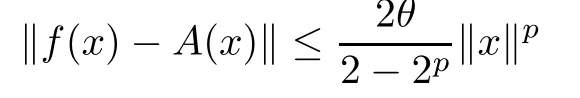
for each x ∈E1. Moreover, if f(tx) is continuous in t for each fixed x ∈E1, then the function A is linear.

However, Aoki did not prove the last part of Theorem 1.9, that is, if f(tx) is continuous in t for each fixed x ∈E1, then the function A is linear. Later, Rassias [18] noted that the proof of Theorem 1.9 can be applied to the case p<0. Afterwards,Gajda[9]complemented Rassias’result (Theorem 1.9) in the case of p>1 and gave an example to show that Theorem 1.9 fails when p=1.

Theorem 1.10([9]) Let E1be a normed space,E2be a Banach space, and f :E1→E2be a function. If there is a real number p such thatand f satisfies the functional inequality

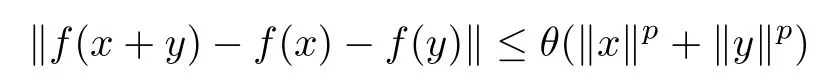
for some θ ≥0 and for all x,y ∈E1?{0}, then there exists a unique additive mapping A:E1→E2such that

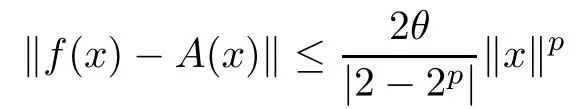
for each x ∈E1?{0}. Moreover, if f(tx) is continuous in t for each fixed x ∈E1?{0}, then the function A is linear.

In 1994, Theorem 1.10 was generalized by Gˇavrut?a [12] by replacing the right hand side of(1.3) in Theorem 1.10 by a general control function as follows:

Theorem 1.11([12]) Let G be an commutative group, E be a Banach space, and φ :G →E be a function satisfying

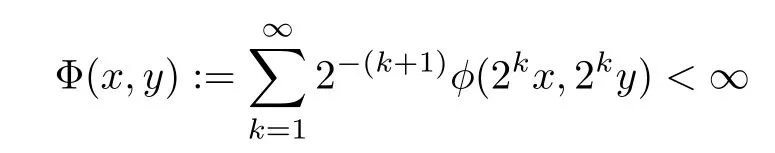
for all x,y ∈G. If f :G →E satisfies the functional inequality

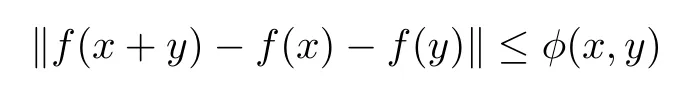
for all x,y ∈G, then there exists a unique additive mapping A:G →E such that

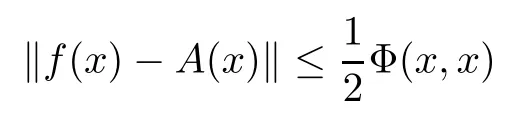
for all x ∈G.

In 2013, Brzd?ek and Ciepli′nski gave stability and hyperstability results for the Cauchy functional equation up to the case of p ∈R as follows.

Theorem 1.12([7]) Let E1and E2be normed spaces and f : E1→E2be a function.Assume that there is a real number p such that p≠1 and f satisfies the following inequality

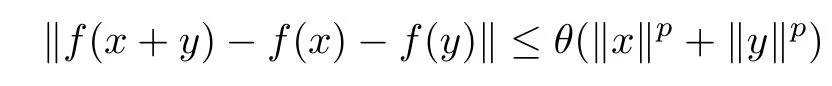
for some θ ≥0 and for all x,y ∈E1?{0}.

? If p ≥0 and E2is complete, then there exists a unique additive mapping A : E1→E2such that

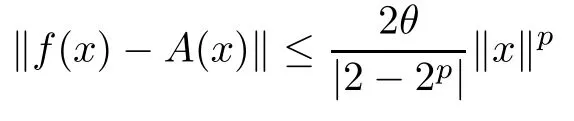
for each x ∈E1?{0}.

? If p<0, then f satisfies

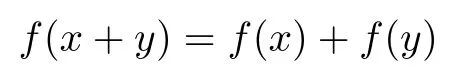
for each x,y ∈E1.

This theorem shows that we obtain the stability results of the Cauchy functional equation in the case p ≥0 while we receive the hyperstability results of the Cauchy functional equation in the case p<0.

Recently, Brzd?ek and Ciepli′nski [8] prove the fixed point theorem in 2-Banach spaces and gave its applications to the stability of the Cauchy functional equation in 2-Banach spaces.Here, we give the main stability result of Brzd?ek and Ciepli′nski [8] as follows.

For a group (G,?), AutG denote the family of all its automorphisms by

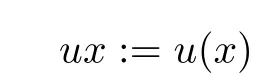
for all x ∈G, u ∈GGand

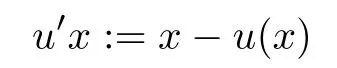
for all x ∈G and for all u ∈GG, where a,b ∈N.

Theorem 1.13([8]) Let (G,+) be a commutative group,(Y,)be a 2-Banach space,and Y0be a subset of Y containing two linearly independent vectors, and h:G0×G0×Y0→R+be a function such that

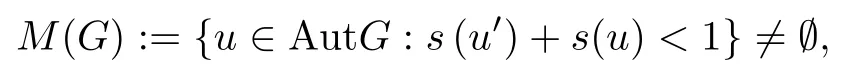
where s(u):=inf{t ∈R+: h(nx,ny,z)≤th(x,y,z) for all x,y ∈G0,z ∈Y0} for u ∈AutG. If f :G →Y satisfies the following inequality

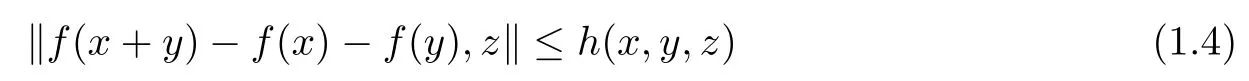
for all x,y ∈G0,z ∈Y0, then, for any nonempty and commutative U ?M(G), there exists a unique generalized Cauchy function T :G →Y such that

for all x ∈G0and z ∈Y0, where

Nowadays,several extensions of the stability and hyperstability results of the Cauchy functional equation have been investigated by many mathematicians. One of such extensions can be considered as the generalized form of the Cauchy functional equation(see[1,3,5,7,14–16]).

Inspired by the above facts, we are interested in studying the stability of the generalized Cauchy functional equation of the form

where a,b ∈N and f is a mapping from a commutative semigroup (G,+) to a 2-normed space(Y,). Our results are extensions of main results of Brzd?ek and Ciepli′nski [8].

2 Auxiliary Tools

In a few decades, many mathematicians investigated several stability results of various functional equations by using the fixed point method in many spaces. For instance, Brzdek [6]proved the Ulam’s type stability of the additivity Cauchy functional equation of the form

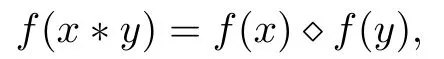
where f is a mapping from a commutative semigroup (G1,?) to a commutative group (G2,?),by using the following fixed point theorem in metric spaces.

Theorem 2.1([6]) Let X be a nonempty set, (Y,d) be a complete metric space, and f1,f2: X →X be given mappings. Assume that T : YX→YXis an operator satisfying the inequality

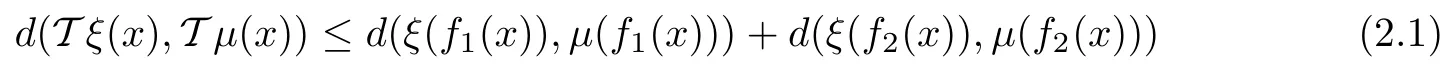
for all ξ,μ ∈YXand x ∈X. Suppose that there exist functions ε : X →R+and ? : X →Y such that for each x ∈X, we have

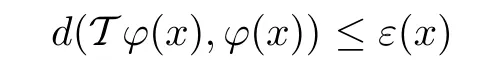
and

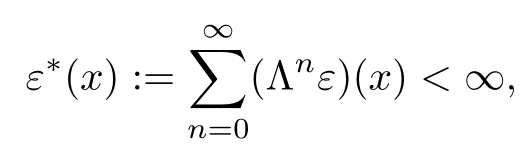
for all x ∈X.

Afterwards,Aiemsomboon and Sintunavarat[2]used the same fixed point theorem with[6]for proving the stability result of the generalized Cauchy functional equation of the form

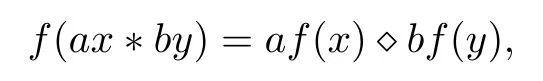
where a,b ∈N and f is a mapping from a commutative semigroup (G1,?) to a commutative group (G2,?), which is the generalized Brzdek’s result in [6].

In 2018, Brzd?ek and Ciepli′nski [8] proved the stability of the Cauchy functional equation in 2-Banach spaces by using the following fixed point result.

Theorem 2.2([8]) Let U be a nonempty set, (Y,) be a 2-Banach space, and Y0be a subset of Y containing two linearly independent vectors, k ∈N, fi: U →U, gi: Y0→Y0,and Li: U ×Y0→R+are given mappings for i = 1,2,··· ,k. Suppose that T : YU→YUis an operator satisfying the inequality

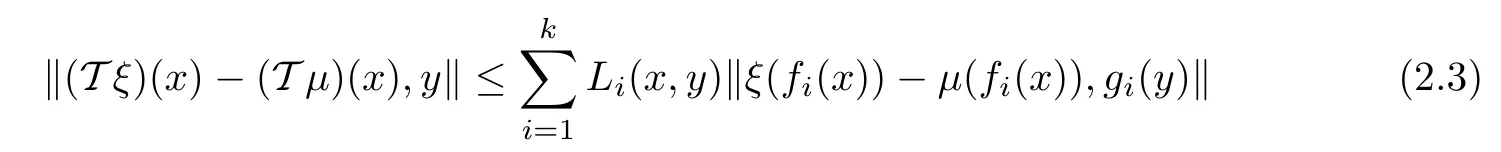
for all ξ,μ ∈YU, x ∈U, and y ∈Y0. Assume that there are functions ε : U ×Y0→R+and ?:U →Y fulfil the following conditions for each x ∈U and y ∈Y0:

and

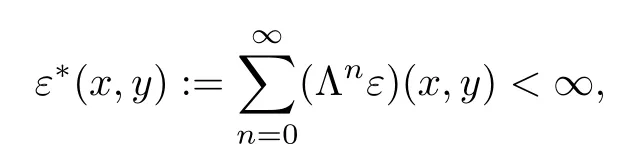
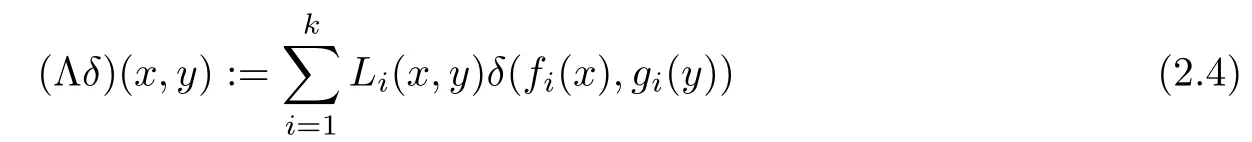
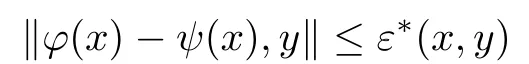
for all x ∈U and y ∈Y0.

3 Approximation of the Generalized Cauchy Functional Equation(1.6)

For a group (G,?), AutG denote the family of all its automorphisms by

for all x ∈X, u ∈GGand

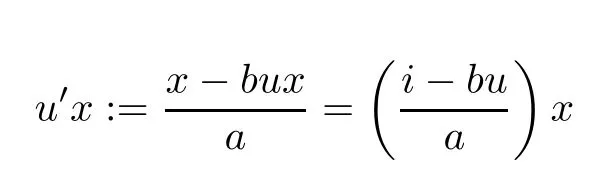
for all x ∈G and for all u ∈GG, where a,b ∈N and i is an identity function from G into its self.

Theorem 3.1Let a,b be two fixed natural numbers, (G,+) be a commutative group such thatand aG0,bG0?G0, (Y,) be a 2-Banach space, and Y0be a subset of Y containing two linearly independent vectors, and h : G0×G0×Y0→R+be a function such that

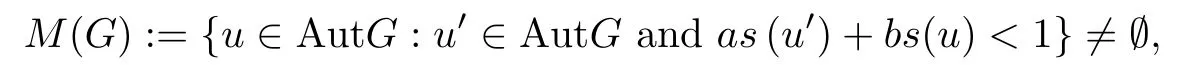
where s(u) := inf{t ∈R+: h(ux,uy,z) ≤th(x,y,z) for all x,y ∈G0,z ∈Y0} for u ∈AutG.

Suppose that f :G →Y satisfies the following inequality

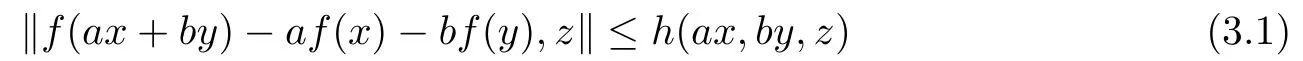
for all x,y ∈G0and z ∈Y0. Then, for any nonempty and commutative U ?M(G), there exists a unique generalized Cauchy function T :G →Y such that

for all x ∈G0and for all z ∈Y0, where

ProofFix a nonempty and commutative U ?M(G). First of all, we will show the first important fact for going to the next step. Note that if u ∈U ?M(G), then we have u,u′∈AutG. This implies that ux,u′x ∈G0for all x ∈G0. It follows from aG0,bG0?G0that

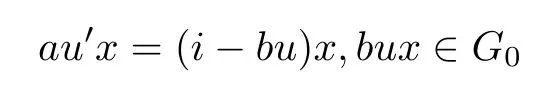
for all x ∈G0.

On the basis of the above fact, for each u ∈U, x ∈G0, and z ∈Y0, replacing x by u′x and y by ux in (3.1), we obtain

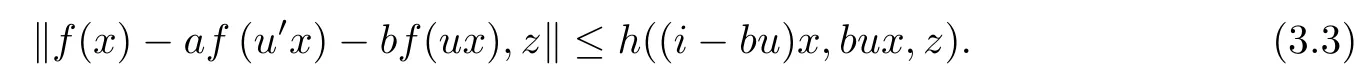
For each u ∈U, we define operators Tu:YG0→YG0andby

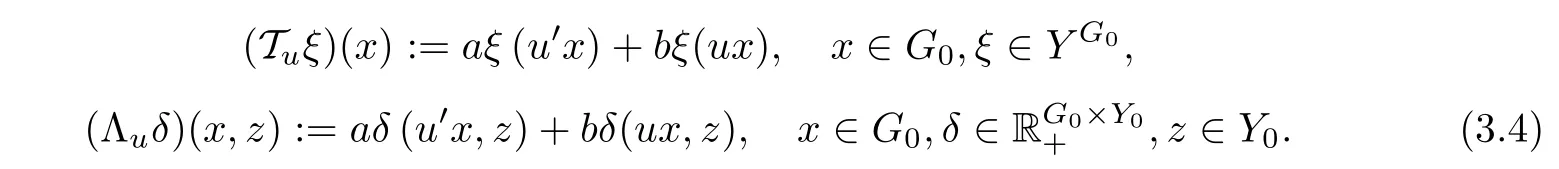
Then, it is easily seen that, for each u ∈U, Λ := Λuhas the form described in (2.4) with U := G0, k = 2, L1(x,z) = a,L2(x,z) = b,g1(z) = z = g2(z), f1(x) = u′x, and f2(x) = ux.

Then, inequality (3.3) follows that

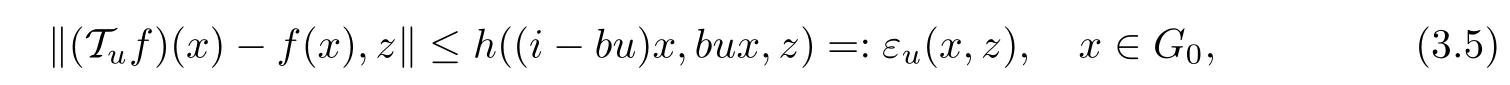
and

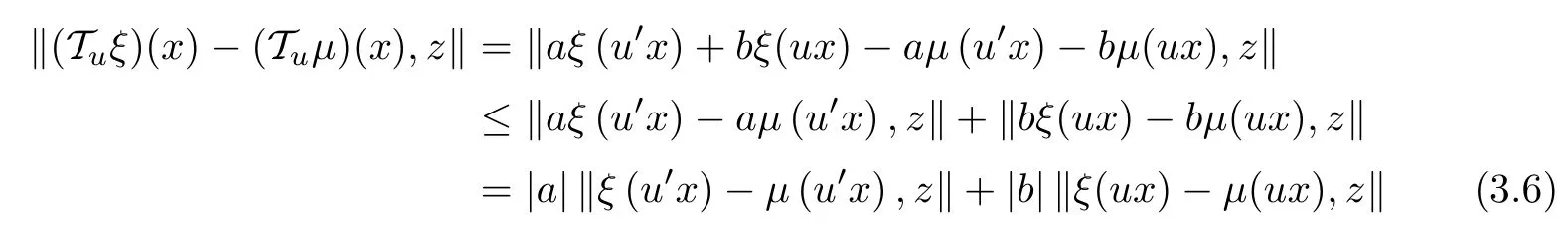
for all u ∈U,ξ,μ∈YG0, x ∈G0, z ∈Y0. Consequently, for each u ∈U, condition (2.3) is valid with T :=Tu.

By the definition of s(u), we have

for all u ∈U, x,y ∈G0, and z ∈Y0. Next, we will show that

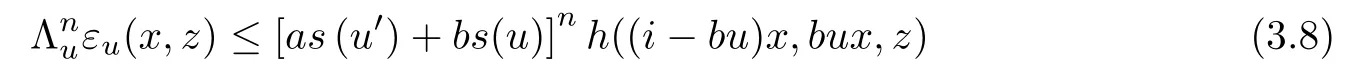
for all n ∈N0, u ∈U, x ∈G0, and z ∈Y0. It is easy to see that condition (3.8)holds for n=0.

From (3.4), we have

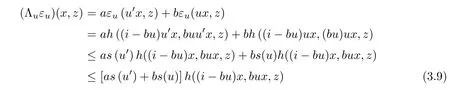
for all u ∈U, x ∈G0, and z ∈Y0. From the above relation, we obtain

for all u ∈U, x ∈G0, and z ∈Y0. In the same way, we get

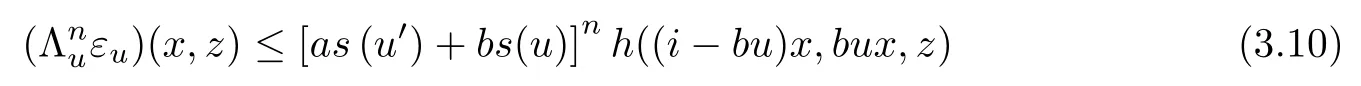
for all n ∈N0, u ∈U, x ∈G0, and z ∈Y0. For u ∈U, x ∈G0, and z ∈Y0, we get

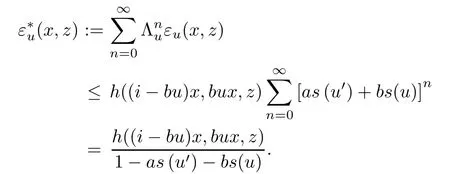
Now, we apply Theorem 2.2 with ε=εuand ?=f. According to it, the limit

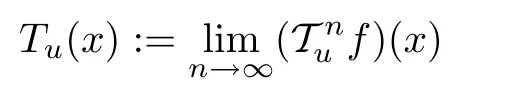
exists for each u ∈U and x ∈G0, and

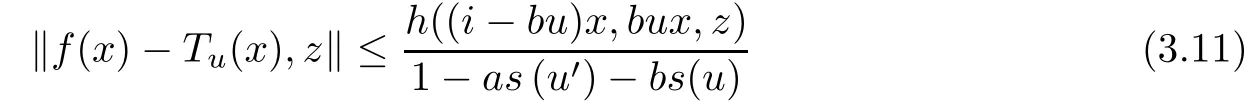
for all u ∈U, x ∈G0, and z ∈Y0.

Next, we will show that

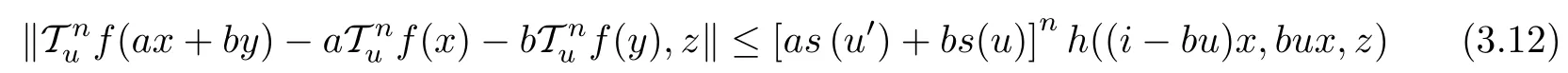
for all n ∈N0, u ∈U, x,y ∈G0, and z ∈Y0. As the case n = 0 is just (3.1), take k ∈N0and assume that (3.12) holds for n=k and every x,y ∈G0with ax+by ∈G0, n ∈N0and u ∈U.

Then

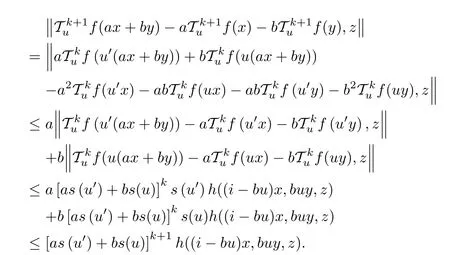
By mathematical induction,we have shown that(3.12)holds for every x,y ∈G0with ax+by ∈G0, n ∈N0, and u ∈U. Letting n →∞in (3.12)and using Lemmas 1.6 and 1.7,we obtain the equality

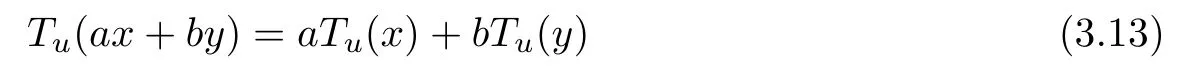
for all x,y ∈G0, u ∈U and the function Tu: G →Y, defined in this way, is a solution of the equation

Next, we will prove that each generalized Cauchy function T :G →Y, satisfying the inequality

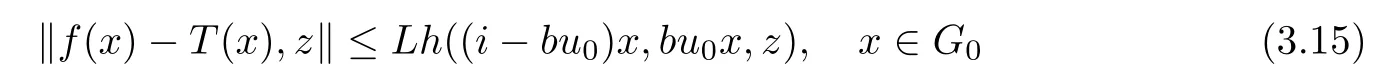
with some L> 0, is equal to Tu0for each u0∈U. To this end, fix u0∈U and the generalized Cauchy function T :G →Y satisfying (3.15). Then, we observe that

where L0= L(1 ?as()?bs(u0))+1 (the case h(x) ≡0 is trivial, so we exclude it here).Observe yet that T and Tu0are solutions to equation (3.14) for all u0∈U. We will show that for each j ∈N0, we have

The case j = 0 is exactly (3.16). So, fix l ∈N0and assume that (3.17) hold for j =l. In view of (3.16), for each u0∈U, we obtain

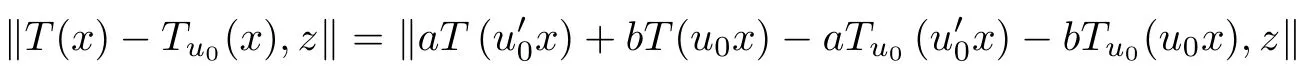
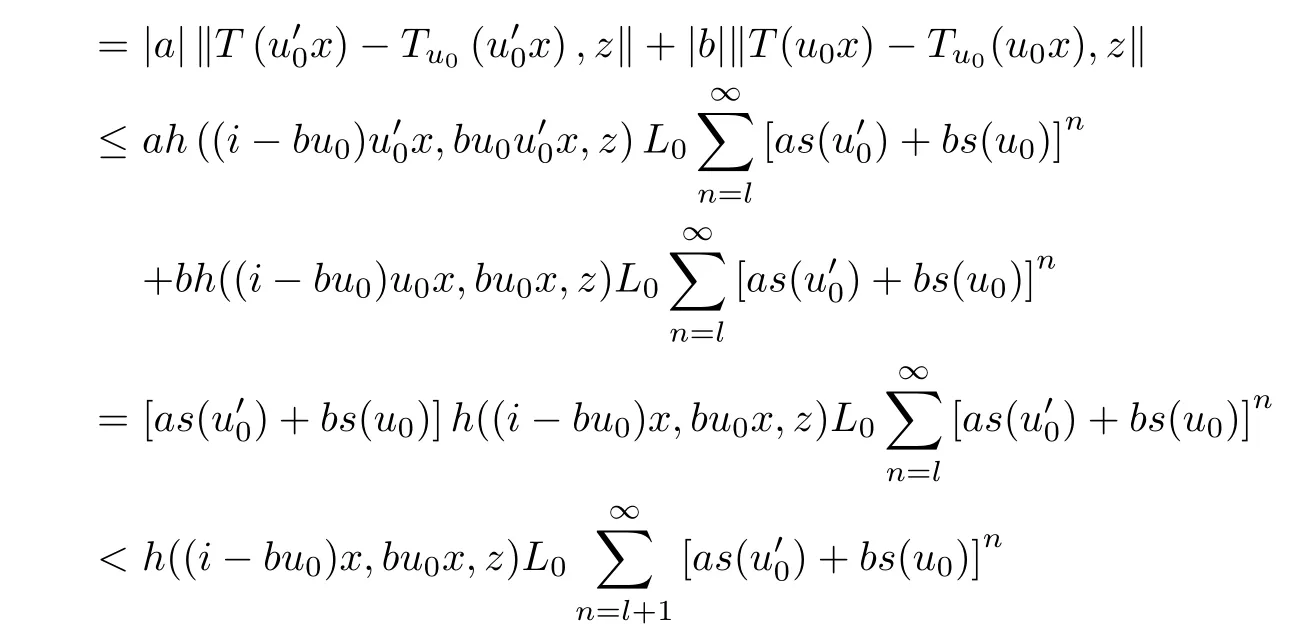
for all x ∈G0and z ∈Y0. Thus, we have shown (3.17). Now, letting j →∞in (3.17) and using Lemmas 1.6, we get

Thus, we have also proved that Tu=Tu0for each u ∈U, which (in view of (3.11)) yields

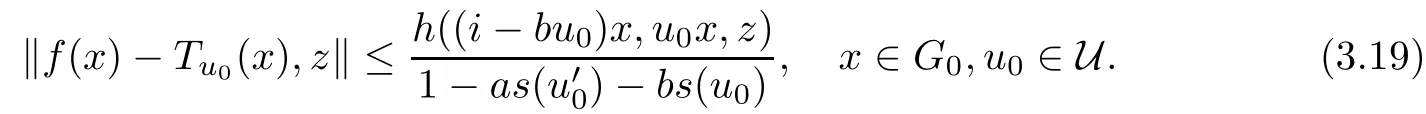
This implies (3.2) with T := Tu; clearly, equality (3.18) means the uniqueness of T as well.

This completes the proof.

Remark 3.2Note that for fixed two natural numbers a,b, there are many illustrative examples of a commutative group G such that

We give some examples of such groups as follows:

? a commutative group(R,+), where+is a usual addition,with any two natural numbers a,b;

? a commutative group (Z2,+2), where +2is a addition modulo 2, with any two positive odd numbers a,b;

? a commutative group (G,·), where

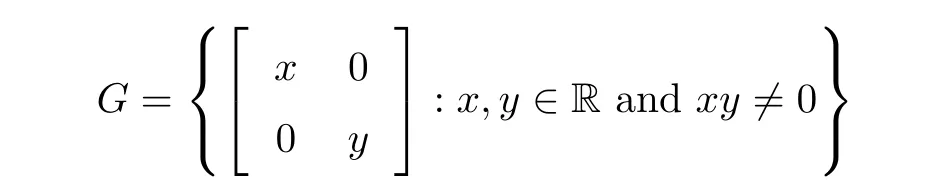
and · is a matrix multiplication, with any two positive odd numbers a,b:

? a commutative group (G,·), where

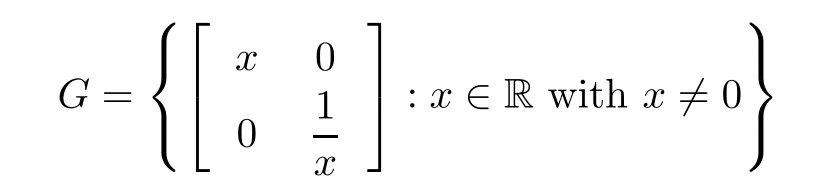
and · is a matrix multiplication, with any two natural numbers a,b.

It is easily seen that Theorem 3.1 yields the subsequent corollary in 2-Banach spaces.

Corollary 3.3([8]) Let (G,+) be a commutative group such that(Y,) be a 2-Banach space, and Y0be a subset of Y containing two linearly independent vectors, and h:G0×G0×Y0→R+be a function such that

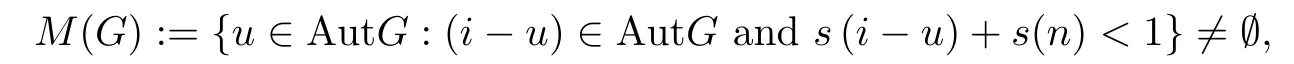
where s(u) := inf{t ∈R+: h(ux,uy,z) ≤th(x,y,z) for all x,y ∈G0,z ∈Y0} for u ∈AutG.Suppose that f :G →Y satisfies the following inequality

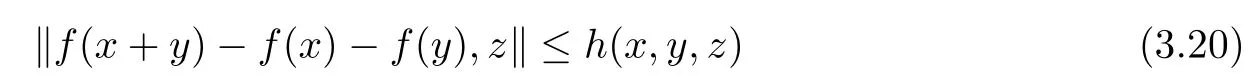
for all x,y ∈G0and z ∈Y0. Then, for any nonempty and commutative U ?M(G), there exists a unique generalized Cauchy function T :G →Y, such that

for all x ∈G0and z ∈Y0, where

ProofThis result can be obtained from Theorem 3.1 by taking a=b=1.

Remark 3.4By using the same technique in Corollary 6.2 of Brzd?ek and Ciepli′nski[8],we get the generalized results on the inhomogeneous generalized Cauchy equation. Furthermore,we can apply Theorem 3.1 with the same technique in the proofs of Corollaries 6.4–6.7 for obtaining the several generalized results corresponding to the hyperstability outcomes from[8].