李遵先,茍長義

(天津理工大學(xué)理學(xué)院,天津 300384)

0 引言

傳染病對人類社會的發(fā)展具有重要影響.傳染病所引起的人類死亡數(shù)遠超過去所有戰(zhàn)爭所導(dǎo)致的人口死亡數(shù)[1].用數(shù)學(xué)建模方法來研究傳染病的傳染規(guī)律是研究傳染病并對其進行控制的有效方法之一.自1927年文獻[2-3]提出SIR倉室模型以來,大量的描述傳染病的數(shù)學(xué)模型被建立,可見文獻[1,4].文獻[5]給出了一個經(jīng)典的SIR傳染病模型：

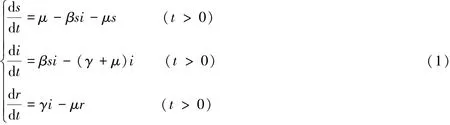
模型(1)將人口分為易感者、感染者以及恢復(fù)者三類.其中：s=s(t),i=i(t)和r=r(t)分別代表t時刻三類人口所占總?cè)丝诘谋壤?正參數(shù)μ,β,γ分別代表出生(死亡)率、感染率和恢復(fù)率.方程(1)等價于：

考慮模型(2)的初值問題,文獻[5]有如下結(jié)論.

命題1設(shè) (s(t),i(t))為方程組(2)在 T={(s,i)s≥0,i≥0,s+i≤1}中的解.記若σ≤1或i(0)=0,則所有從T中出發(fā)的軌道趨于平衡點(1,0).若σ＞1,則存在正平衡點(se,ie)=,使得當(dāng)i(0)＞0時,所有從T中出發(fā)的軌道均趨于此正平衡點.

基于模型(2)的眾多傳染病模型被建立,近期工作如文獻[6-11].由命題1知,模型(2)具有閾值稱為基本再生數(shù).其生物意義為單位時間內(nèi)每個感染者傳染易感者個數(shù).以下考慮具擴散的模型(2)是否仍有此閾值性質(zhì)?一般地,無擴散時平衡態(tài)的穩(wěn)定性與具擴散時不同,即Turing不穩(wěn)定性[12].如文獻[13]考慮一類具擴散的傳染病模型,得到當(dāng)基本再生數(shù)大于1時,無論是否存在擴散項,無疾平衡點(態(tài))均不穩(wěn)定.但文獻[14]在研究一類具年齡結(jié)構(gòu)的捕食-被捕食模型時,得到其無擴散時的平衡點在考慮擴散效應(yīng)后從不穩(wěn)定變成了局部漸近穩(wěn)定,即產(chǎn)生了Turing不穩(wěn)定性.為此,考慮以下系統(tǒng)：

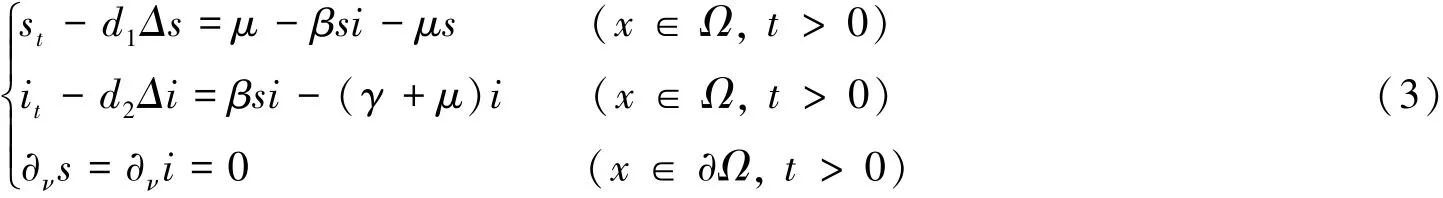
其中：Δ為Laplace算子,Ω?Rn是一個具光滑邊界?Ω的有界區(qū)域.齊次Neumann邊界條件表明模型(3)是封閉的,即在邊界上沒有人口的流入和流出.模型(3)對應(yīng)的平衡態(tài)方程如下：

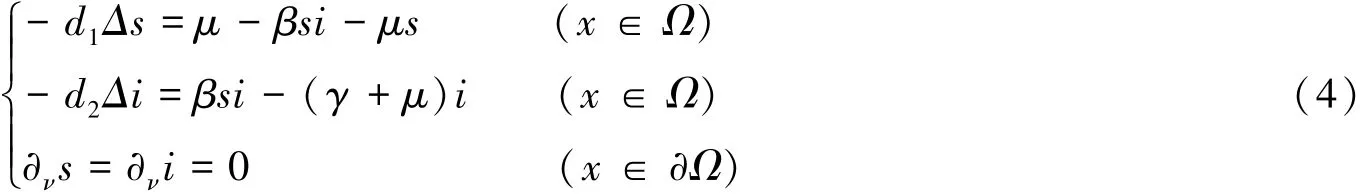
易見,當(dāng)σ≤1時,系統(tǒng)(4)有一個非負常數(shù)平衡態(tài)(1,0)；當(dāng)σ＞1時,系統(tǒng)(4)有兩個非負常數(shù)平衡態(tài)(1,0)和(se,ie)=.以下分析此模型(3)的非負常數(shù)平衡態(tài)的(局部)穩(wěn)定性.

1 平衡態(tài)的穩(wěn)定性分析

參照文獻[15],令0=λ0＜λ1＜λ2＜λ3＜…是 -Δ在區(qū)域Ω上具Neumann邊界條件的特征值,并令X={(s,i)∈[C1(Ω)]2：?νs=?νi=0,x∈?Ω},E(λ)={φ： - Δφ =λφ,x∈Ω, ?νφ =0,x∈?Ω}(λ∈R).設(shè)是 E(λi)的一組標(biāo)準正交基,以及 Xij={cφij：c∈ R2},那么.其中：

當(dāng)σ＜1時,對非負平衡態(tài)(1,0),有如下結(jié)論.

定理1若σ＜1,模型(3)的平衡態(tài)(1,0)是局部漸近穩(wěn)定的.

證明 將模型(3)的平衡態(tài)(1,0)平移到(0,0)得：

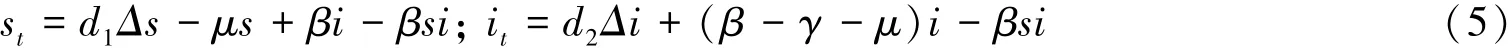
方程(5)的線性化方程為：

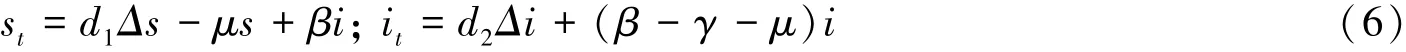
相應(yīng)地,當(dāng)σ＞1時,對非負平衡態(tài)(1,0)和(se,ie),有如下兩個結(jié)論.

定理2若σ＞1,模型(3)的平衡態(tài)(1,0)是不穩(wěn)定的.

證明 與定理1證明類似,因考慮平衡態(tài)(1,0)的穩(wěn)定性問題需考慮算子L1的特征值分布情況.由于此時σ ＞1,即β-γ-μ＞0.從而無法得到對任意j={0,1,…},都有det A1j＞0及Tr A1j＜0成立.事實上,取j=0,可知：

由此可知A10存在具正實部的特征值,故(1,0)不穩(wěn)定.

定理3若σ＞1,模型(3)的平衡態(tài)(se,ie)是局部漸近穩(wěn)定的.

證明 與定理1證明類似,將模型(3)的平衡態(tài)(se,ie)平移到(0,0)得：

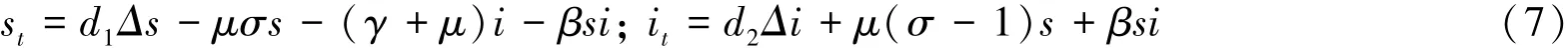
方程(7)的線性化方程為：

2 數(shù)值模擬

如下對模型(3)進行數(shù)值模擬.參考文獻[5,13],分別取以下兩組方程參數(shù)：

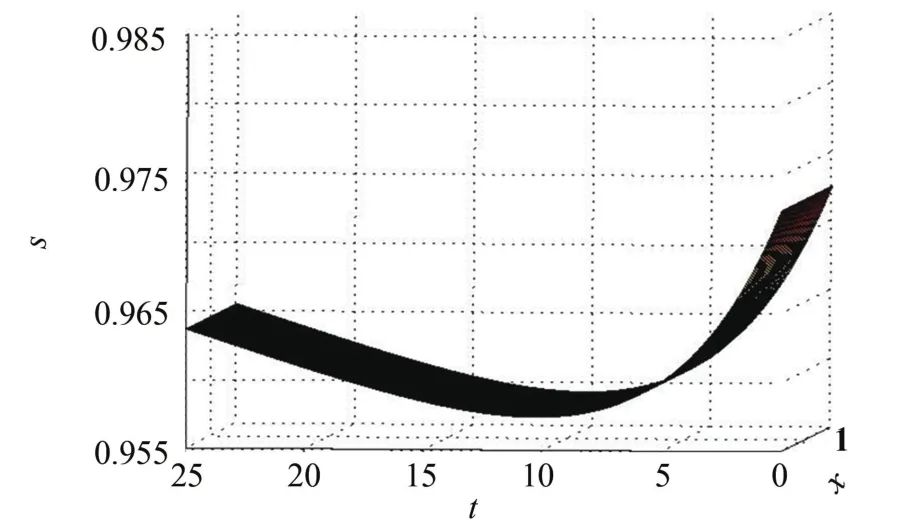
圖1 s(x,t)趨于1Fig.1 s(x,t)tends to 1

由圖1～2可見,平衡態(tài)(1,0)局部漸近穩(wěn)定.當(dāng)σ=3時,模型(3)數(shù)值模擬如圖3～4所示：

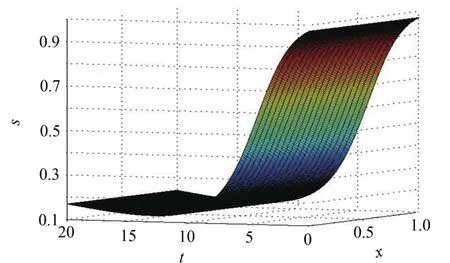
圖3 s(x,t)趨于0.333 3Fig.3 s(x,t)tends to 0.333 3

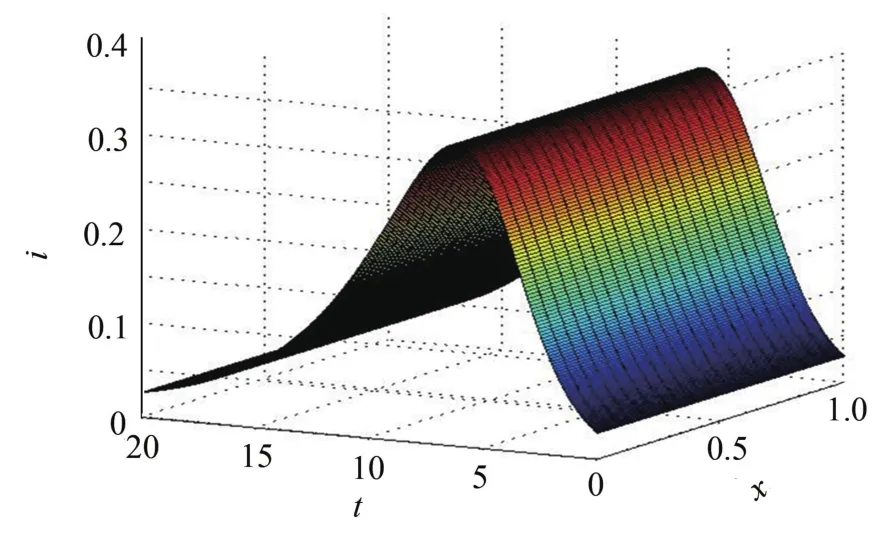
圖4 i(x,t)趨于0.031 7Fig.4 i(x,t)tends to 0.031 7

由圖3～4可知,此時平衡態(tài)(1,0)不穩(wěn)定且(se,ie)局部漸近穩(wěn)定.

3 結(jié)果與討論

1)由定理1～3知,具擴散的SIR傳染病模型具有與命題1類似的閾值性質(zhì),即對于模型(3),決定平衡態(tài)穩(wěn)定性的仍然是基本再生數(shù),而與擴散無關(guān).

2)命題1考慮了σ=1的情況,但定理2～3沒有考慮此情形.作為此臨界問題,需要進一步討論方程高階項的情況,這將在后續(xù)工作中考慮.

3)由圖4可知,當(dāng)σ＞1時,傳染病在傳染初期出現(xiàn)局部的峰值即小的爆發(fā),這一結(jié)論對模型(3)也存在[5].

4 附錄

附錄 1aj? det A1j=d1d2+{μd2-(β -γ -μ)d1}λj-μ(β -γ -μ) ＞ 0,bj?Tr A1j=-(d1+d2)λj+(β-γ-μ)-μ ＜0.設(shè)為A1j的兩個特征值,故=aj＞0,+=bj＜0.對任意j={0,1,…},考慮兩種情況：

附錄2已知aj?det A2j=d1d2+ μσd2λj+ μ(σ -1)(γ + μ) ＞ 0,bj?TrA2j=-(d1+d2)λjμσ ＜0.設(shè)為A2j的兩個特征值,故-=aj＞0,+=bj＜0.?j={0,1,…},考慮兩種情況：