Ravi V. Gandhi,, and Dipak M. Adhyaru

Abstract—This paper introduces a Takagi-Sugeno (T-S) fuzzy regulator design using the negative absolute eigenvalue (NAE)approach for a class of nonlinear and unstable systems. The open-loop system is initially embodied by the traditional T-S fuzzy model and then, all closed-loop subsystems are combined using the proposed Max-Min operator in place of traditional weighted average operator from the controller side to lessen the coupling virtually and simplify the proposed regulator design.For each virtually decoupled closed-loop subsystem, the composite regulators (i.e., primary and secondary regulators) are designed by the NAE approach based on the enhanced eigenvalue analysis.The Lyapunov function is utilized to guarantee the asymptotic stability of the overall T-S fuzzy control system. The most popular and widely used nonlinear and unstable systems like the electromagnetic levitation system (EMLS) and the inverted cart pendulum (ICP) are simulated for the wide range of the initial conditions and the enormous variation in the disturbance.The transient and steady-state performance of the considered systems using the proposed design are analyzed in terms of the decay rate, settling time and integral errors as IAE, ISE, ITAE,and ITSE to validate the effectiveness of the proposed approach compared to the most popular and traditional parallel distributed compensation (PDC) approach.

I. INTRODUCTION

MOST of the real-time physical systems and processes are nonlinear by nature. Also, a massive range of nonlinear applications belong to the class of unstable dynamical systems such as an inverted pendulum, magnetic levitation system, ball, and beam system. This class of benchmark systems demands efficient mathematical modeling to present the nonlinear behavior as well as an effective regulator design to provide the stabilization against the unstable behavior.Investigation reveals that among the existing fuzzy models,Takagi-Sugeno (T-S) fuzzy models have been widely used as a universal approximator to model and to control their natural unstable and nonlinear behaviors via model-based fuzzy control systems [1]. The Sugeno type fuzzy model was first introduced using the well-known “IF-THEN” rules for the linguistic variables in the premise part for a given set of system data while linear combinations of input and output in the consequent part [2]. As a foundation of the T-S fuzzy model, Sugeno model was modified and upgraded to develop a more versatile and efficient fuzzy model to present the local dynamics of the linear and time-invariant (LTI) subsystems in the consequent part [3].

Development of the T-S fuzzy model for the given nonlinear system is described in [3]. Because of the LTI dynamics in the consequent part, the T-S fuzzy model has been widely used with the conventional state feedback control approach for regulating each local subsystem. One of the most popular and widely applied control approaches is the parallel distributed compensation [4]. The central idea of the parallel distributed compensation (PDC) approach is to control the dynamics of each local subsystem using the eigenvalue analysis [4], [5].

Most of the researches related to the stability analysis of the PDC based T-S fuzzy regulators have been carried out extensively using the sets of linear matrix inequalities (LMIs)in the 1990s [3]?[8]. To reduce the stability conditions and number of LMIs, relaxed LMI conditions based regulator and observer design have been proposed [9], [10]. Different methodologies have been presented in the various literature to overcome the stability issues of finding the common positive definite matrixPfor a set of LMIs. A few of earlier approaches are: searching of the common matrix under pairwise commutative assumption [11], variable structure based local regulator design [12], compensation and division for fuzzy models [13], decentralized PDC controller design using the interaction of the subsystems [14]. Numerous methods using the Lyapunov synthesis as dual controller design [15], the Lyapunov’s direct method based nonlinear controller design[16],maximum overlapped rule group based on standard fuzzy partitioning [17], [18] have been applied to the nonlinear applications.

Various techniques like matrix search using alternate interval approach for the nominal as well as an uncertain T-S fuzzy system[19]?[22],eigenvalue constraints-based approach[23],have been discussed. Some other recent approaches like BMI linearization based multiple model approach[24],single dominant regulator design for all the subsystem [25], a multivariable T-S fuzzy system with parametric optimization [26],performance-oriented PDC based on required cost [27] were also utilized for several applications.Investigation reveals that the stability analysis for the traditional T-S fuzzy regulator based on the PDC approach has been carried out extensively using most common quadratic Lyapunov function. To consider the effect of the various T-S fuzzy model parameters,researchers have proposed various non-quadratic Lyapunov function based approaches like non-quadratic stabilization of uncertain system [28], exponential stability with guaranteed cost control [29], [30], piecewise continuous and smooth function [31], piecewise continuous exact T-S models [32],non-quadratic membership dependent higher order [33], sum of square (SOS) based polynomial membership function [34],[43], superstability conditions [35], fuzzy c-regression state model to implement the data-driven T-S fuzzy model [38],integral structure based Lyapunov function [44], subspacebased improved sector nonlinearity approach [45], fractional intelligent approach [49], new interpolation function based approach [50], membership function dependent Lyapunov-Krasovskii function[46],[51],robust pole-placement approach[47].Event-triggered control for nonlinear systems[52],adaptive neural networks-based tracking control and fault-tolerant control [53], [54] have been introduced to present the effectiveness of intelligent control.

An in-depth survey of the stability analysis and regulator for the T-S fuzzy control system has been presented in [36].Controllability conditions and simplified regulator have been introduced to overcome the complexity and difficulties of the traditional approach for the T-S fuzzy system [37]. Based on the presented literature survey, the traditional approach using PDC for the stabilizing control and LMIs for the stability analysis may introduce the computational burden, complexity and the coupling of subsystems [13], [35].

The proposed approach is motivated by the approaches as,1) the methodology used in [12], [36], to virtually reduce the coupling as well as to simplify the design of the T-S fuzzy regulator, and 2) usage of the eigenvalue analysis in[23], and forming the superstability conditions in place of the formulation of the LMI to obtain the regulator gains in each different cases for the considered nonlinear systems presented by the T-S fuzzy model in [35].

In approach 1), the maximum firing strength (h) based dominant state feedback gain (Kk) is considered for all the subsystems, i.e.,Kk= argmaxi{hi},i= 1,2,...,r. But, the usage of the single dominant feedback gain (Kk) for all the local subsystem may disturb the stability of the overall closedloop system [12]. In approach 2), the eigenvalue analysis or superstability conditions may be applicable to the specific class of systems. To enhance the performance of the Max operator based dominant feedback gain (Kk), the additional Min operator is introduce as discussed in depth in the following section. Also, to confirm the stability for the wide range of the nonlinear and unstable systems, the negative absolute eigenvalue (NAE) approach is proposed.

The key contribution of the proposed research work for the class of nonlinear and unstable systems is as follows:

1) In this paper, the T-S fuzzy regulator design is discussed in a modest way to lessen the structural complexity among the closed-loop subsystems from the controller side.A unique

Max-Min operator is introduced for selecting the dominant values of friing strengthand the regulator gains (KPandKs) respectively. In case of the traditional PDC approach,the weighted average operator is used, which introduces the coupling and complexity among the closed-loop subsystems.However,the structural simplification may degrade the regulator effectiveness which is well remunerated by introducing the secondary T-S fuzzy compensating regulator (us). A similar kind of compensation with different design has been proposed in many researches [13]?[16].

2)A simplified T-S fuzzy regulator design using the concept of eigenvalue analysis instead of the LMI approach is prescribed. The detailed analysis to guarantee the asymptotical stability in large with the sufficient condition is carried out using the widely used quadratic Lyapunov function. Step by step procedure to calculate the tuning parameters involved in the proposed T-S fuzzy regulator design is described in the Section III.

3) The efficacy of the proposed design based on the NAE approach is validated using the simulation of nonlinear and unstable electromagnetic levitation system and inverted pendulum on a cart for the nominal as well as under, a) the broad range of initial conditions, b) the variable step change of disturbances. Transient and steady-state characteristics like decay rate, settling time and various standard integral errors(i.e., integral square error (ISE), integral time square error(ITSE),integral time absolute error(ITAE),and integral absolute error(IAE))based on the proposed approach are analyzed and compared with the traditional PDC approach with and without the variation of disturbances.

This paper is structured as follows:Section II introduces the preliminaries of the T-S fuzzy model, PDC based regulator design and LMIs for stability analysis using the quadratic Lyapunov function.Also,the problem statement is formulated based on the literature survey presented to overcome the design complexity of the traditional PDC approach for stabilizing the nonlinear systems. In Section III, the Max-Min operator is introduced to reduce the coupling among the subsystems.Next, the negative absolute eigenvalue (NAE) approach is proposed to obtain the primary and secondary T-S fuzzy regulator gains for each decoupled subsystem to guarantee the stability of the given nonlinear system in large. Section IV presents the simulation results to validate the efficacy of the proposed approach compared to the traditional PDC plus LMI approach for the given nonlinear control applications like electromagnetic levitation system[39]?[42],and inverted pendulum on cart [3]?[5] followed by concluding remarks.

II. PROBLEM FORMULATION AND PRELIMINARIES

A. Takagi-Sugeno (T-S) Fuzzy Model

Takagi-Sugeno proposed an efficient way to describe any given nonlinear system as a group of linear subsystems [3].This can be done either using the concept of sector nonlinearity or using the concept of local approximation [5]. A T-S fuzzy model based on sector nonlinearity forith plant rule can be represented as [5]

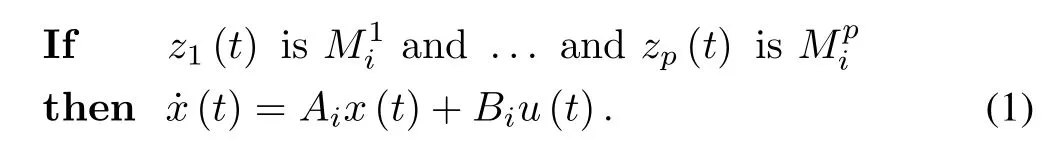
The overall T-S fuzzy model with the number of plant rules and control rules beingrcan be expressed by [5],

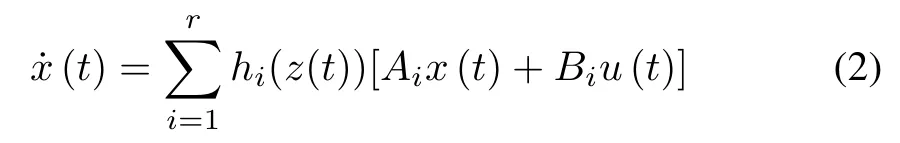
wherehi(z(t)) is the normalized membership grade

and

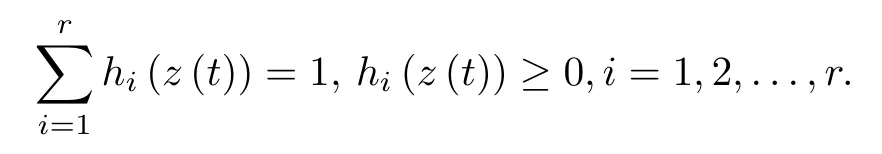
B. Parallel Distributed Compensation (PDC)

To stabilize the nonlinear system represented by a T-S fuzzy model (2), the concept of PDC [4] is one of the widely used control approaches. Regulator based on the PDC utilizes the sets of fuzzy rules as (1). Theith control rule based on the PDC with local state feedback gain (Ki) can be represented as

Overall nonlinear regulator based on weighted averageoperator based defuzzification can be expressed by [5]

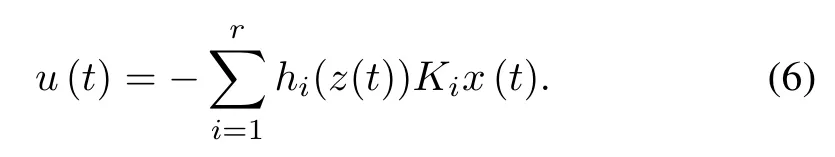
Substituting(6)into(1)results in the following closed-loop dynamics:

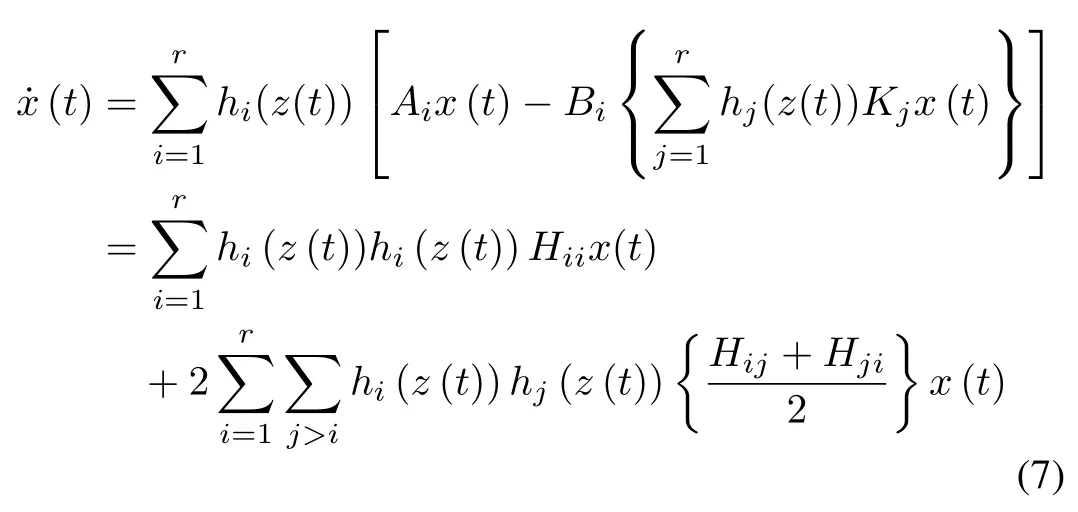
where

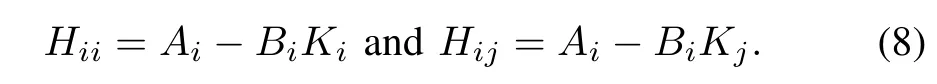
C. Stability Analysis and LMI Approach

Sufficient conditions for the stability of the given nonlinear system in the large operating region are derived using the Lyapunov’s direct method [5], [6]. The equilibrium point of the closed-loop T-S fuzzy system(7)is globally asymptotically stable if there exists a common positive definite matrix P such that the following conditions are satisfied [5]:

Fori= 1,2,...,randj > iwith all the pairs of(i,j) expecting the pair as?hi(z(t))hj(z(t)) = 0,?t >0.Reconstructing the inequalities by pre and post-multiplying by theP?1, following LMIs can be obtained as [7], [8].

where

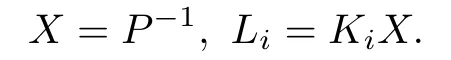
Hence,a solution of LMIs presented by(11)and(12)would provide the required regulator gains (Ki) and stability matrix(P).

D. Formulation of Problem Statement

As discussed in [13], the traditional PDC approach for designing the global state feedback regulator (6) uses the weighted average operator such that everyith local state feedback regulator gain (Ki) affects its own subsystem (Hii)as well as all other subsystems (Hij) which may introduce the virtual coupling and structural complexity among the closed-loop subsystems [13]. To guarantee the stability of the overall virtually coupled closed-loop system (7) using the PDC approach, sufficient conditions mentioned by (9) and(10) must be satisfied. One of the popular and widely used methodologies to solve this feasibility problem is to form the groups of LMIs as(11)and(12).One may observe that a larger number of nonlinearities or premise variables(p)would results in a greater no. of rules (r=2p) as well as larger number of LMIs (l= Σr=r(r+1)/2) presented by (7) for the given nonlinear system. For example, if the nonlinear plant having no.of premise variables asp=4 which demandsr=16 andl= 120 as shown in Fig.1 to obtainKiandPfor the effective stabilizing control in the case of the traditional PDC + LMI approach.

Also, variation in the disturbance or initial conditions demands additional computation for the PDC based regulator gains under the LMI framework [3]?[5]. Solving a huge number of LMIs may cause the computational burden and structural complexity with a large number of stability conditions. For several nonlinear control applications, there may not be a feasible solution via the LMI approach based on given stability conditions (9) and (10) [35].

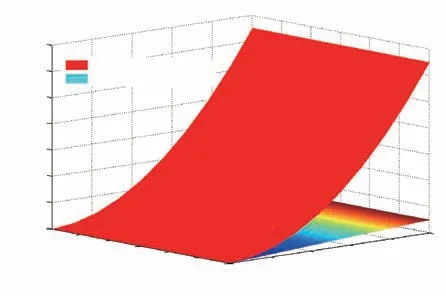
Fig.1. Comparison of No. of rules and No. of LMIs with respect to No. of premise variables.

Consider the following subsystems as described in (8):

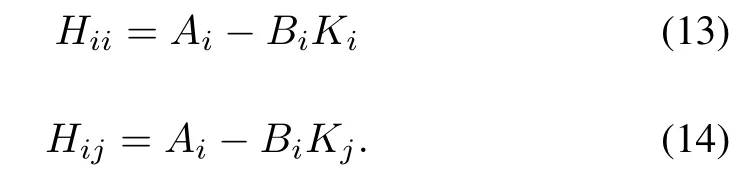
The set of subsystems expressed by (13) and (14) are considered as decoupled subsystem and coupled subsystem respectively in this paper. For example, if the given nonlinear system is modeled with T-S fuzzy rules described by (1)withr= 3 then no. of subsystems (ns) can be computed byns= Σr ?ns=6 as described by

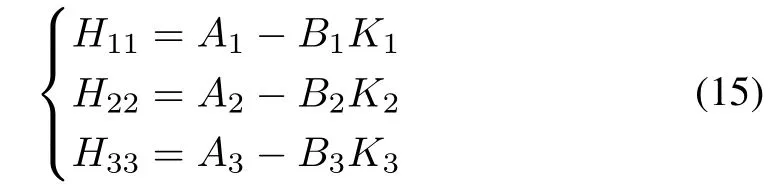
and

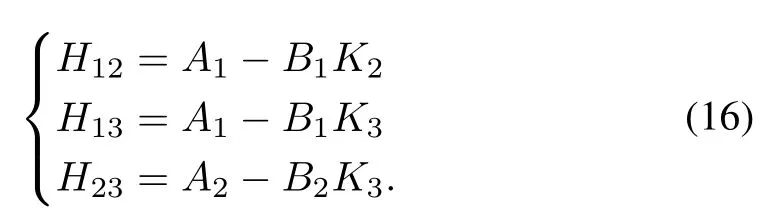
It can be observed from (13) and (14) that the decoupled subsystems rely only on their own regulator gains (Ki) while coupled subsystems also rely on the regulator gains (Kj) of other subsystems. Coupled subsystems are mostly influenced by the regulator gains of other subsystems which causes the structural complexity, no. of rules, large no. of stability conditions and ultimately the computational burden for the design of T-S fuzzy regulators using the PDC plus LMI approach.

III. NEGATIVE ABSOLUTE EIGENVALUE(NAE)APPROACH

The negative absolute eigenvalue (NAE) approach is primarily used for the unstable systems having one or more positive (unstable) eigenvalues. This research utilizes the unstable dynamics of the considered system in designing the T-S fuzzy regulator gains. It can be proved that the negative of the absolute real eigenvalue for any given system would be absolute negative.On this fundamental,the proposed approach is developed to solve the stabilizing control problem using the T-S fuzzy regulator design.

Assumption 1 [12]:It is assumed that each of the local subsystem used to develop the T-S fuzzy closed-loop global model is locally controllable with each (Ai,Bi) pair and observable with each (Ai,Ci) pair fori=1,2,...,r.

Under this assumption the local state feedback regulator(ui)fori=1,2,...,rcan be designed using the conventional eigenvalue approach such that eigenvalues of each closed-loop subsystem stay in the sufficient left side to the imaginary axis.To reduce the influence presented in the coupled subsystems due to one local regulator gain on second regulator gain as discussed earlier, the Max-Min operator is introduced in this study. Max operator is accountable for selecting the dominant value of the local firing strength (hi(z(t))) and Min operator for choosing the optimal value of local state feedback regulator gain (Ki) which is composed of primary (KP) and secondary(Ks) gains as follows:

Using the above Max-Min operator in place of the weighted average operator in (5) and (6) would result in the following overall nonlinear control law (u(t)):

whereuP(t) is the primary state feedback regulator law anduS(t) is the secondary high gain compensating regulator law.Both the regulators (KPandKs) are designed based on the proposed approach to support the T-S fuzzy closed-loop control system against the reduction of subsystems as well as confirm the eigenvalues of each closed-loop subsystems in the sufficient left side from the imaginary axis for allt>0.

Substituting (20) into (2) yields the proposed simplified stabilizing regulator based overall closed-loop T-S fuzzy global model

Remark 1:It is observed that using the traditional PDC approach described by (6), there exists coupling due to the multiplication of two terms: 1)and 2)For the proposed approach, coupling due to the multiplication of two terms has been reduced and replaced by a single decoupled term:described in (17)?(19).

Remark 2:Total number of subsystems required to form(22) isrfor the proposed approach which is around/2 in case of the traditional PDC approach.

Remarks 1 and 2 imply that the proposed control approach simplifies the structure of the overall closed-loop system by reducing the total no. of subsystems. When coupling among the subsystems is virtually minimized using the proposed approach,the total number of LMIs used to obtain the solution gets drastically reduced from l toras shown in Fig.1.

Expanding (21) would result in the following:

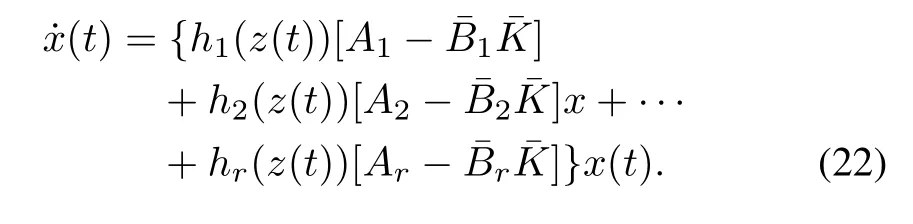
Remark 3:It can be observed from the expanded dynamics of (22) that the Max-Min approach based T-S fuzzy closedloop system is a combination of the weighted average of decoupled closed-loop subsystems.

It is noted that due to the reduction of subsystems, the overall performance of the T-S fuzzy system may degrade.The secondary high gain regulator(Ks)is utilized to compensate the performance degradation of the closed-loop system.Max-Min operator based decoupled system can be effectively stabilized by proper selection of the primary and secondary regulator gains as proposed by Theorem 1. Finally, the stabilizing regulator for the given T-S fuzzy regulatory system has been designed based on following theorem to confirm the stability.

Notations:symbolizing an eigenvalue of the matrixMbyλ(M),and highest and lowest eigenvalues ofMbyλmax(M),andλmin(M), then the following result explain the stability conditions for the overall closed-loop control system described by (21).

Theorem 1:Suppose the T-S fuzzy system described by (2)is locally controllable. Then the T-S fuzzy closed-loop system described by (21) is asymptotically stable if the proposed T-S fuzzy regulator is designed using the desired location of the closed-loop poles based on the negative absolute eigenvalue(NAE) approach as follows:

Proof:Here,andare the desired location of the closed-loop poles for the primary and secondary regulator gainsthe negative absolute eigenvalue of aopen-loop subsystem;is the vector of the negative biased eigenvalue to avoid any zero or positive values for the desired location of the closedloop poles,is the elementwise (*)multiplying factor for the high gain secondary regulator(us)to provide compensation against the decoupling of the subsystem;is a vector of maximum eigenvalue out of available local models;is therth component ofβ >0 is the common scaling factor for the selection ofαbased on the following pseudo-code:

Considering the widely used quadratic Lyapunov function(QLF) candidateV(x) =x(t)T Px(t) the time derivative ofV(x)along the solution of (2) is

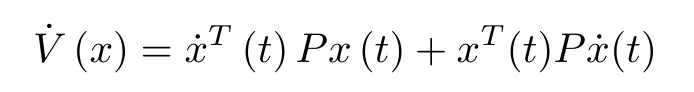
Substituting the dynamics of ˙x(t)from(22)would result in

where

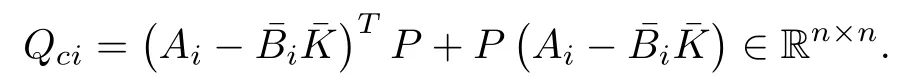
Using equality mentioned in [12], one has

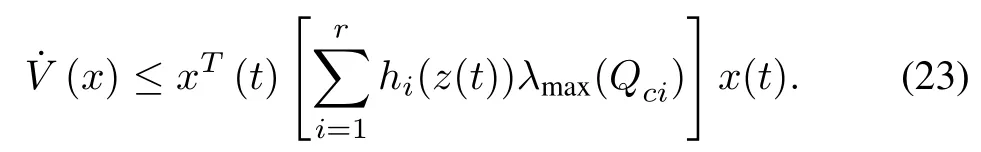
It can be further reduced to (23) using Lemma 2,

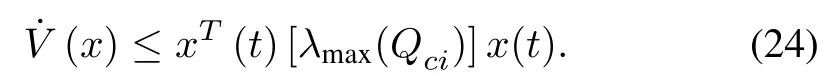
Once,λmax(Qci)<0 is guaranteed then based on Lemma 1,the closed-loop stability of the T-S fuzzy system is also confirmed.

Where

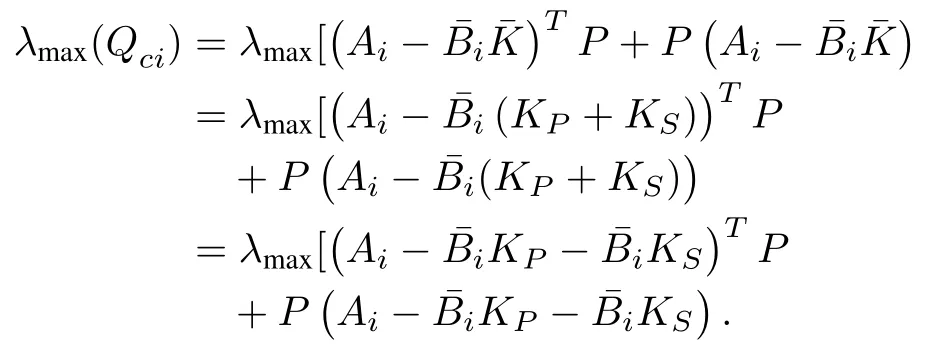
Based on Weyl’s inequality [24] and simplification in the above dynamics, the upper bound of the maximum negative eigenvalue can be expressed by

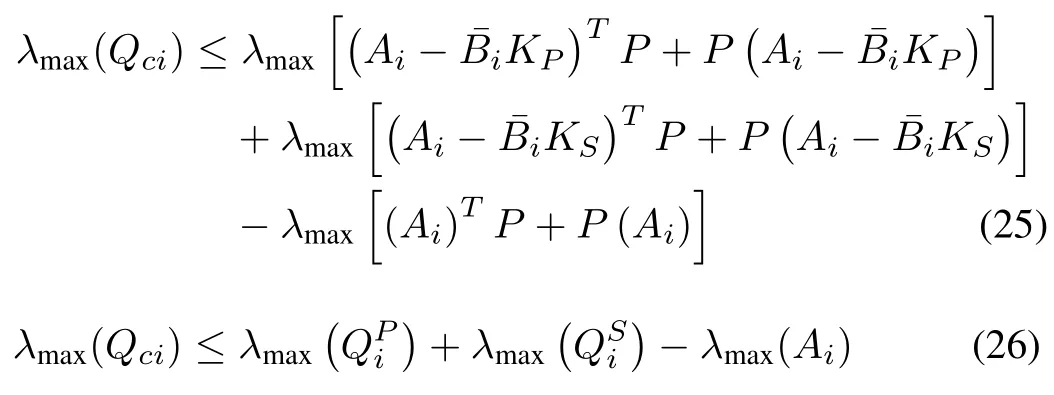
where

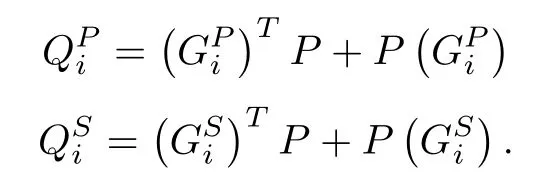
Using the NAE approach, the closed-loop eigenvalues of all the decoupled subsystems remain in the sufficient left half plane of the origin. This would result in the following conditions:

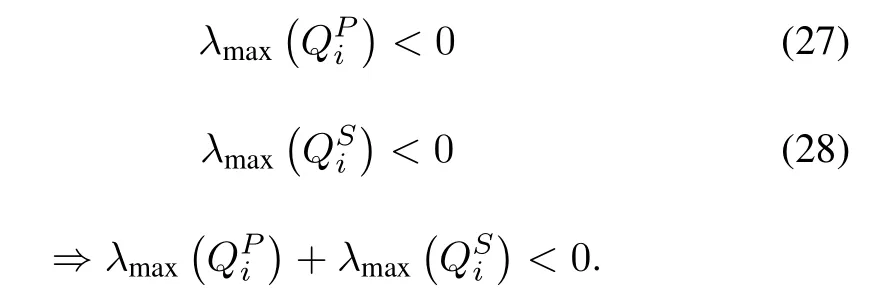
It can be confirmed based on the proposed approach by selecting the proper value ofβ >0 for the open loop unstable subsystems withλmax(Ai)≥0 such that the following condition holds.

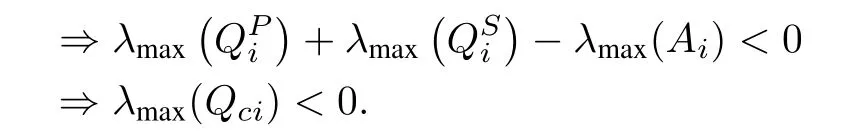
Hence, the stability of the T-S fuzzy regulator based closed-loop system using the NAE approach is guaranteed.

Theorem 1 involves many design parameters and subconditions which need to clarify for the successful application of the proposed approach.

The steps to design the NAE based T-S fuzzy regulator gains for a class of nonlinear and unstable systems are as follows:

1) Design an open-loop traditional T-S fuzzy model for the given system represented by (1)?(3).

2) From the open-loop T-S fuzzy model, obtain the eigenvalues of local subsystems asλ(Ai),i=1,2,...,r.

3) Select negative values for the biasing vectorδbto avoid any closed-loop poles on origin.

4) Calculate the location of closed-loop poles to obtain the primary regulator gainsusing the pole-placement as follow:

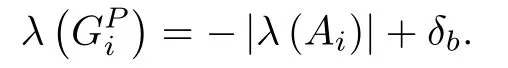
5) Find the multiplying factor (αk) based on the described pseudo algorithm withβranging from 1.2 to 3.5.

6) Calculate the location of closed-loop poles to obtain the secondary regulator gainsusing the pole-placement as follow:

7) Finally, the dominant values of the regulator gainand the membership gradecan be obtained using the Max-Min operator as described by (17)?(19).

8) Use the obtained values of the design parameters if the following condition is satisfied.

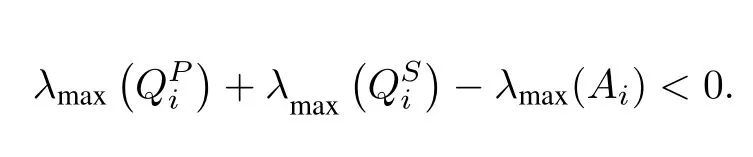
9) If the above condition is not satisfied, then go to Step 3 and re-calculate the design parameters.

Remark 4:It can be observed that the proposed T-S fuzzy regulator gainshave been designed using the pole-placement approach which can be determined using the eigenvalues of considered open-loop subsystems. Also, the eigenvalues of all the closed-loop subsystems will always be in the left half of thes-plane due to negative absolute eigenvaluesirrespective of the unstable nature of the open-loop eigenvalues.

IV. SIMULATION RESULTS

This section presents the simulation of two different nonlinear and unstable systems under the framework of the proposed T-S fuzzy regulator. The prime objective of the simulation is to validate the effectiveness of the designed regulator for the wide range of the initial conditions and the enormous variation in the bounded disturbance.

A. Electromagnetic Levitation System (EMLS)

The nonlinear and unstable current controlled EMLS in Fig.2 is considered for the stabilizing control of steel ball position (y) around the operating position (y0). The nonlinear dynamics of EMLS can be expressed by

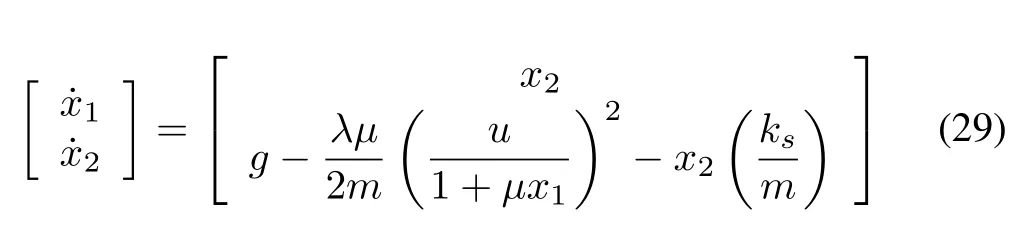
wherex1denotes the vertical position of the steel ball,x2is a vertical velocity,uis the coil current as a control action.g=9.81 m/s2is the gravitational constant;m=0.05 kg is the mass of steel ball;λ=0.460 H, μ=2 m?1andks=0.001 Ns/m are the positive constants described in[39].

As the equilibrium points for the EMLS are nonzero and unstable [42], [47], the coordinate transformation has been performed to develop the sector nonlinearity based T-S model with the following transformed dynamics:

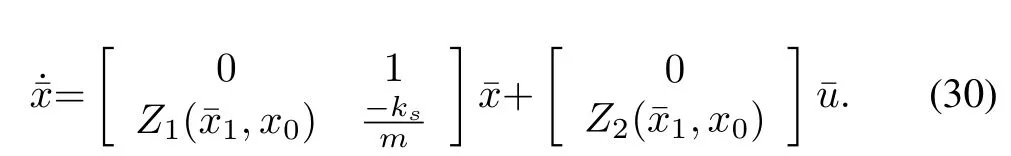
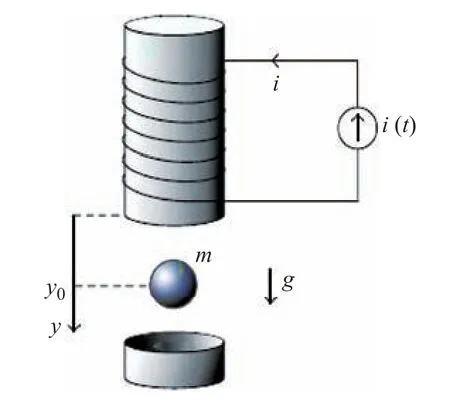
Fig.2. Structure of the electromagnetic levitation system [39].

The T-S model consists of two bounded premise variables with mentioned subsystems and membership functions as shown in Fig. 3 [39]:

The eigenvalues of each open-loop subsystem (Ai) have been computed and obtained negative.This shows the unstable behaviour of all the subsystems as shown in Table I.In case of plane inverted cart pendulum (ICP), subsystems fromA1–A3have one pole in the right half of the imaginary axis.

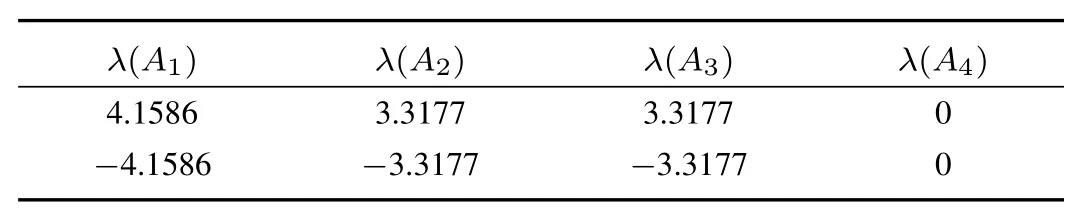
TABLE I EIGENVALUES OF THE OPEN-LOOP EMLS SUBSYSTEMS

To stabilize the EMLS based on the NAE approach and pseudo-algorithm,α= [β β β β]Tandδb= [?1?2]Thave been chosen to avoid marginal stability of subsystemA4observed from Table I and to ensure the close-loop stability of all the local subsystems. Selecting the different values ofβ >0 in the range of 1 to 4 would result in the stabilization of the EMLS with different speed dynamics during the transient as shown in Fig. 4. It has been observed that the steel ball accomplished the stabilization for all the chosen value ofβ. However, for the values ofβas 3 and 4, there is a heavy demand of the coil current which may cause the actuator saturation or heating of the electromagnet.For a small value ofβ(<1) there is a problem of sluggish speed of the stabilization due to less amount of the regulator action.During the simulation, the proposed regulator gave the most satisfactory stabilizing control for 1.5< β <2.25.For the moderate speed of response and saturation free control action,β= 2 is considered as the optimal value throughout the simulation which would result inα=[2 2 2 1]T.

Figs.4 and 5 reveal that the proposed regulator stabilizes EMLS faster, smoother and undershoot free compared to the traditional PDC approach with the settling time (Ts) nearly 0.5 s (nearly 0.75 s for the PDC approach), undershoot of nearly 0%(nearly 8%for the PDC approach),and steady-state error near zero.

Simulation has been performed for a wide range of the initial steel ball positions forβ=2 as shown in Fig. 6. For all the allowable initial ball positions in the range of 3?18 mm,the NAE approach based T-S fuzzy regulator has given the satisfactory results. Various integral errors like ISE, ITSE,ITAE, and IAE have been computed during the 3 s simulation of the EMLS as shown in Table II.

It is observed that the regulator designed using the proposed approach has reduced all of the above mentioned integral errors compared to the PDC approach.The proposed regulator stabilizes all the local subsystems such thatλmax(Qci) ={?15.12?17.16} <0 which guarantees the stability of the given nonlinear system based on the proposed Theorem 1.

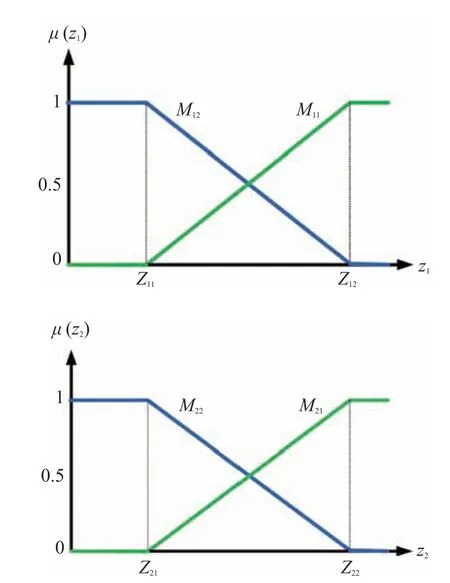
Fig.3. Membership functions for Z1 ∈ [Z11,Z12], and Z2 ∈ [Z21,Z22].

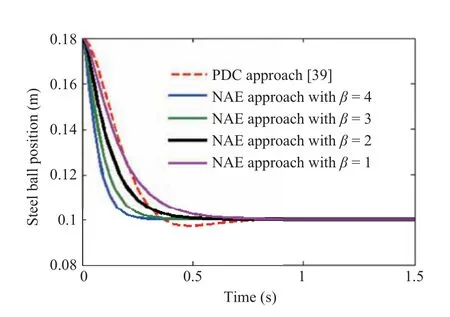
Fig.4. Response of the steel ball position for the different values of β with initial conditions (x(t0)): [0.180]T around x0 =0.1 m.

Fig.5. Response of the proposed regulator for the different values of β with initial conditions (x(t0)): [0.180]T around x0 = 0.1 m.

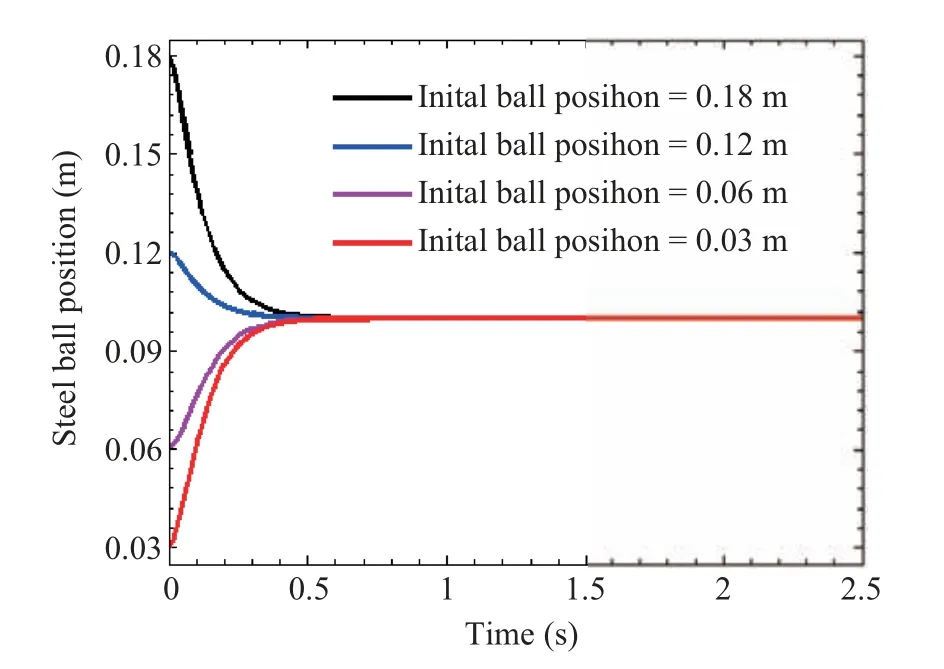
Fig.6. Response of the steel ball position with β = 2 for a wide range of initial positions of the steel ball.

TABLE II COMPARISON OF VARIOUS INTEGRAL ERRORS WITHOUT DISTURBANCE FOR EMLS(SIMULATION TIME=3 S)

Performance of the nonlinear and unstable EMLS is mostly affected by various vertical disturbances.The payload is one of the most common vertical disturbance[41],[42].In this study,to check the performance robustness of the proposed design,the payload in the range of 0?40% of the system weight with variable step change nature is applied after 2 s of the stabilization of the steel ball around 0.1 m as shown in Fig.7.It is clearly remarked that the steel ball maintained the position throughout the simulation of 10 s with only 1 mm deviation under the maximum payload of 40% during the simulation time of the 4 s to 8 s. In the case of the PDC approach, the steel ball lost the stabilization under the payload just beyond 10%.

The coil current required for the stabilization of the steel ball in the presence of the payload for the proposed approach is even less than for the PDC approach throughout as observed from Fig.8. Integral errors like ISE and ITAE have been computed in the presence of the payload for the 10 s simulation as shown in Table III.It is observed that the regulator designed using the proposed approach has greatly reduced all the above mentioned integral errors compared to the PDC approach in the presence of the vertical disturbance.

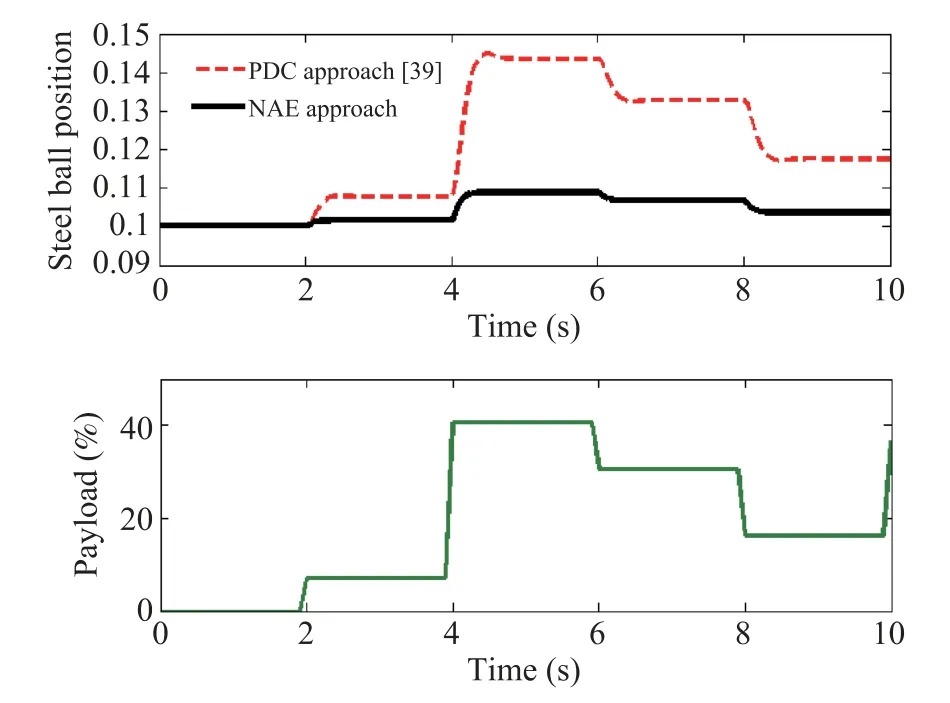
Fig.7. Response of the steel ball position with β = 2 for the enormous step variation of the bounded payload disturbance of 0?40%.

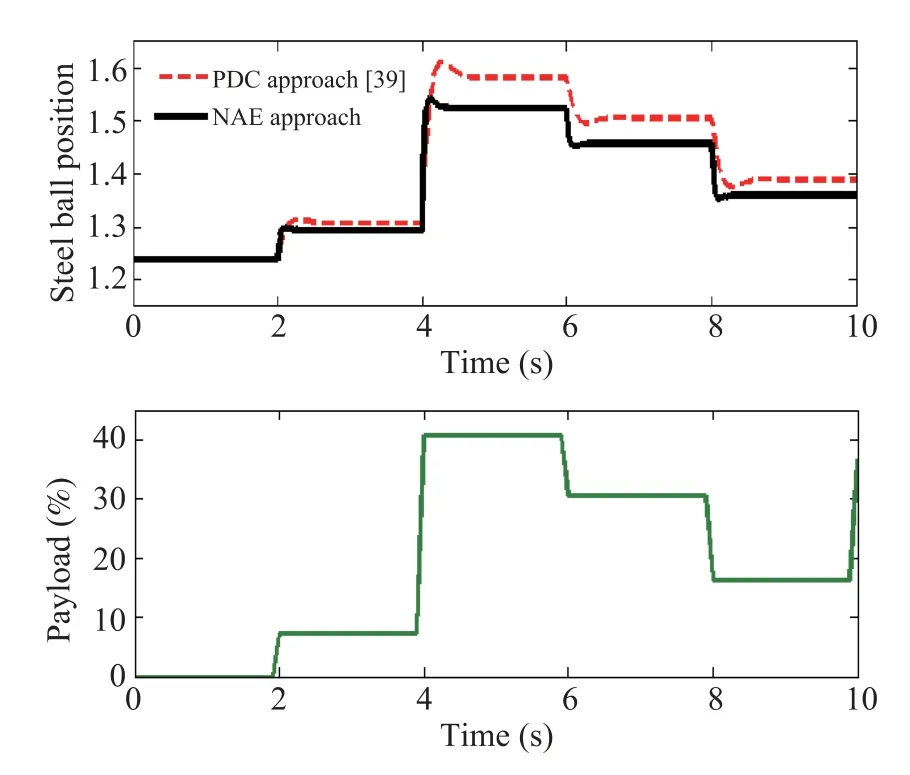
Fig.8. Response of the proposed regulator with β =2 for the enormous step variation of the disturbance of 0?40%.

TABLE III COMPARISON OF VARIOUS INTEGRAL ERRORS IN THE PRESENCE OF THE PAYLOAD FOR EMLS (SIMULATION TIME= 10 S)

The computed values for the NAE approach based local gains of the primary and secondary regulators are as follows:

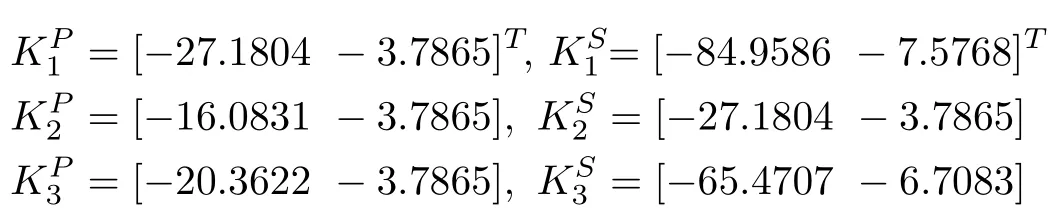
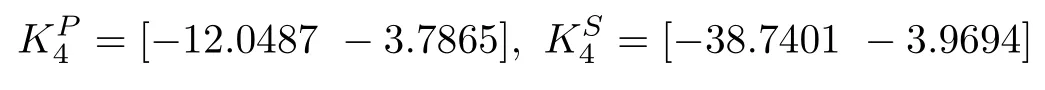
B. Inverted Pendulum on a Cart

The nonlinear inverted cart pendulum in Fig.9 is considered to improve the stabilizing control of pendulum position (θ).Nonlinear dynamics of the given system are follows [4]:

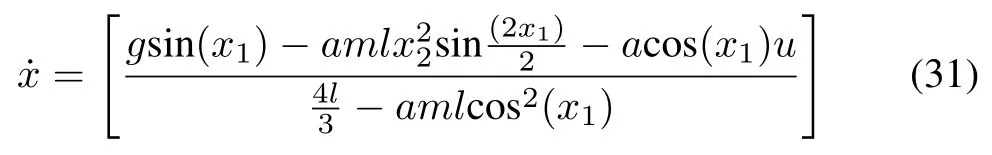
wherex1denotes the pendulum arm angular position with respect to the vertical axis andx2denotes arm angular velocity;g= 9.81 m/s2is the gravitational constant;L= 2l= 1 m is the length of the arm;M= 8 kg is the mass of the cart;m= 2 kg is the mass of the pendulum; anda= 1/m+Mis the force applied to the cart andγ= cos(88?); local approximation based T-S fuzzy models are used to stabilize the arm position of the inverted pendulum on a cart.The main control objective of the subsection is to stabilize the pendulum in the approximate range of?180?to+180?.Above T-S fuzzy model consists of the following 4-subsystems and membership functions as shown in Fig. 10 [39].

The eigenvalues of each open-loop subsystem (Ai) have been computed and found negative which shows the unstable behaviour of all subsystems as shown in Table IV. In the case of the ICP, all the subsystems have one of the poles in the right half plane of the imaginary axis.

TABLE IV EIGENVALUES OF ICP SUBSYSTEMS

To stabilize the ICP based on the NAE approach and pseudo-algorithm,α= [β β β β]Tandδb= [?1?2]Thave been chosen to ensure the closed-loop stability of all the local subsystems. Selecting the different values ofβ >0 in the range of 1 to 4 would result in the stabilization of the ICP with different speed dynamics during the transient as shown in Fig.11. It has been observed that the pendulum arm accomplished the stabilization for all the chosen values ofβ. However, for the values ofβas 3 and 4, there is a giant demand of the force which may cause the damage of the mechanism. For a smaller value ofβ(<1) there is a less amount of force generation.

During the simulation of the ICP, the proposed regulator gave the most satisfactory stabilizing control forβ=2 which would result inα= [2 2 2 2]Tthroughout the simulation of ICP. Figs.11 and 12 reveal that the proposed regulator stabilizes the given nonlinear system quicker, and smoother compared to the traditional PDC approach with the settling time (Ts) nearly 0.8 s (which is nearly 1.45 s for the PDC approach), undershoot of nearly 0 %, and steady-state error near zero. Simulation has been performed for a wide range of the initial arm positions forβ=2 as shown in Fig.13.

For the entire allowable initial ball positions in the range of 30?160 degree, the NAE approach based T-S fuzzy regulator has given the satisfactory results. Settling time for the entire range of the initial conditions is found to be less than 1 s using the proposed design.

Fig.9. Structure of the inverted pendulum on a cart.

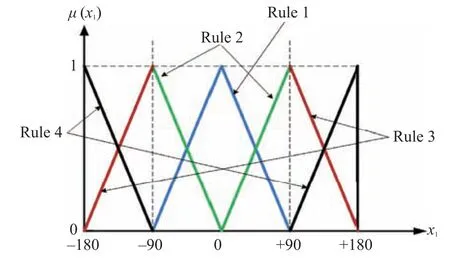
Fig.10. Membership functions for the local subsystems of the ICP.

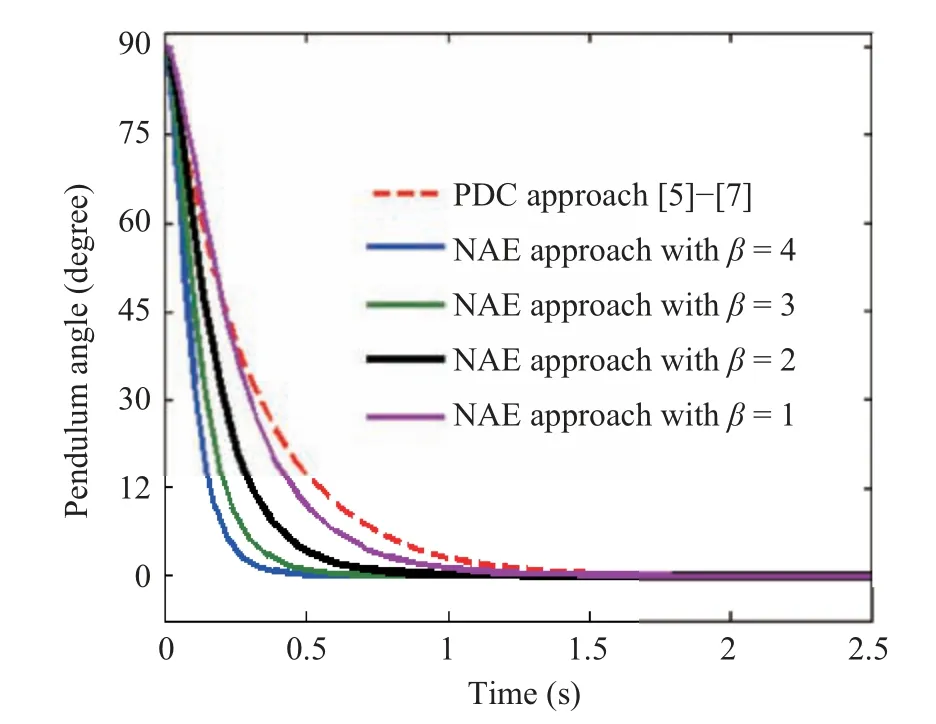
Fig.11. Response of pendulum arm angle for different values of β with initial conditions (x(t0)):[90 0]T.

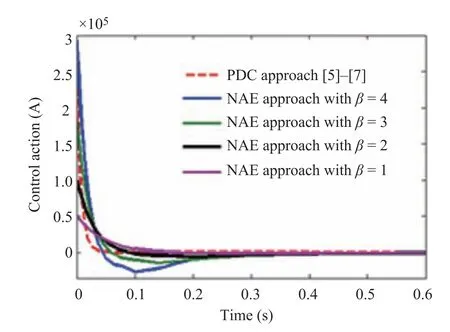
Fig.12. Response of the proposed regulator for the different values of β with initial conditions (x(t0)):[90 0]T.

Fig.13. Response of steel ball with β =2 for a wide range of initial position.

Various integral errors like ISE, ITSE, ITAE, and IAE have been computed during the 3 s simulation of the ICP as shown in Table V. It is observed that the regulator designed using the proposed approach has reduced all the above mentioned integral errors compared to the PDC approach. The proposed regulator stabilizes all the local subsystems such thatλmax(Qci)<0 similar to the EMLS which guarantees the stability of the given nonlinear system based on Theorem 1.

TABLE V EIGENVALUES OF ICP SUBSYSTEMS

Performance of the nonlinear and unstable ICP is mostly affected by the accelerative disturbances. In this study, to check the performance robustness of the proposed design,the accelerative disturbance in the range of?10 to 10 m/s2with variable step change nature is applied after 2 s of the stabilization of the pendulum arm around 45 degrees as shown in Fig.14. It is clearly remarked that the pendulum arm maintained the position throughout the simulation of 10 s with only±1.2 degrees deviation under the maximum disturbance during the simulation time of the 2 s to 6 s. In the case of the PDC approach,the pendulum arm oscillates with the deviation of±4.7 degrees (around 4 times higher than the former).

Fig.14. Response of steel ball with β = 2 for the enormous step variation of the bounded accelerative disturbance of ?10 to 10 m/s2.

The average force required for the stabilization of the pendulum arm in the presence of the accelerative disturbance throughout for the proposed approach is very small and smooth compared to the PDC approach as observed from Fig.15.Integral errors like ISE and ITAE have been computed in the presence of the payload for the 10 s simulation as shown in Table VI. It is observed that the regulator designed using the proposed approach has greatly reduced all the above mentioned integral errors compared to the PDC approach in the presence of the vertical disturbance.

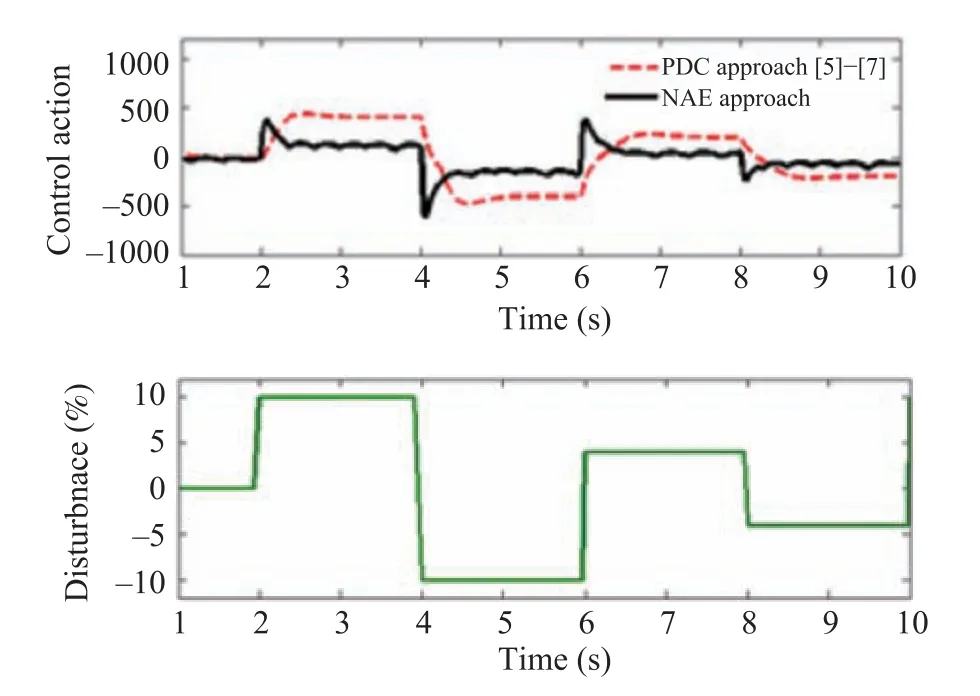
Fig.15. Response of the regulator with β =2 for the enormous step variation of the bounded accelerative disturbance of ?10 to 10 m/s2.

The computed values for the NAE approach based local gains of the primary and secondary regulators are as follows:

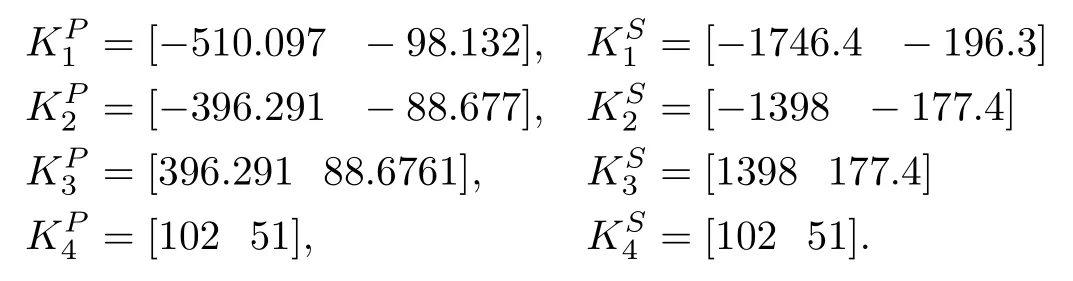
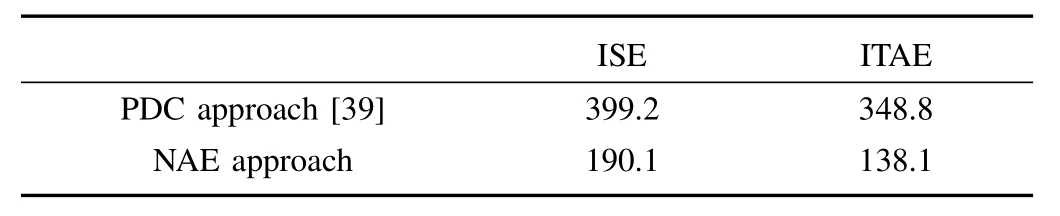
TABLE VI COMPARISON OF VARIOUS INTEGRAL ERRORS FOR ICP(SIMULATION TIME=10 S)

V. CONCLUDING REMARKS

The stabilizing regulator design for the given nonlinear and unstable systems presented by the T-S fuzzy system has been studied. Initially, the closed-loop subsystems have been virtually decoupled using the Max-Min operator from the controller side to simplify the structure and to reduce the number of closed-loop subsystems.The NAE based T-S fuzzy regulator has been designed based on the desired eigenvaluesanddescribed by Theorem 1 to stabilize all the closed-loop subsystems. Then, the sufficient conditions have been derived to guarantee the stability of the overall decoupled closed-loop systems based on the quadratic Lyapunov function using the proposed approach.

Step by step design procedure has been prescribed to calculate the design parameters. The simulation of two different nonlinear and unstable systems for the stabilizing control has been carried out using the PDC approach and the proposed approach for a wide range of the initial conditions. The simulation reveals that the proposed control has provided faster, saturation-free and overshoot-free transient response compared to the PDC based control. It has been revealed by the observation of various integral errors (i.e., IAE, ISE,ITAE, ITSE) that the proposed design has also gained the performance superiority in steady-state compared to the former design. The performance robustness of the proposed regulator design has been guaranteed in the presence of the variable step change of disturbance as well as an assorted range of the initial conditions for both the practical applications.

Finally,from the values obtained for the proposed regulator gainsduring the simulation, it has been revealed that the secondary regulator (us) acted as a high-gain compensating regulator. The values of the multiplying factorα,and parameterβcan be tuned to control the decay rate and the control actions respectively during the transient while the value of the biasδbcan be modifeid to regulate the steadystate.

VI. FUTURE SCOPE

The proposed regulator performs well for the class of nonlinear and unstable systems under, 1) the variable step kind of the disturbance, 2) the fixed values of the design parameters likeα,βandδb, and 3) the constant value of the set-point during the simulation. As an extension to this work, one may analyze the applicability of the NAE approach for the generalized nonlinear system with different kind of the disturbances. The design parameters likeα,βandδbmay be optimized to achieve the desired performance. Finally, the effectiveness of the proposed approach may be compared with the non-PDC approach.