帶Dini核的多線性Calderón-Zygmund算子的迭代交換子的有界性?
周疆,胡喜
(新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,新疆 烏魯木齊 830046)
0 引言
多線性Calderón-Zygmund 理論起源于Coifman 和Meyer 在文獻(xiàn)[1]和[2]中的工作.近幾十年來,帶經(jīng)典核的多線性Calderón-Zygmund 理論被許多學(xué)者進(jìn)一步研究(見文獻(xiàn)[3 ?6]).最近,帶粗糙核的多線性Calderón-Zygmund 理論逐漸形成(見文獻(xiàn)[7 ?13]).首先,我們介紹一類帶粗糙核的多線性Calderón-Zygmund 算子的定義.
設(shè)ω(t):[0,∞)→[0,∞)是一個(gè)非減函數(shù)且0<ω(1)<∞.對于a>0,如果有
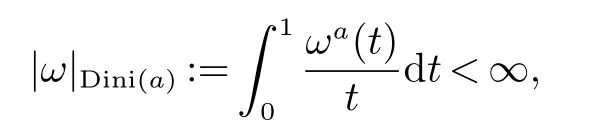
那么稱ω ∈Dini(a).顯然地,若0 其中X ≈Y 表示存在一個(gè)常數(shù)C>0,使得C?1Y ≤X ≤CY. 定義1[11]設(shè)K(x,y1,...,ym)是定義在(Rn)m+1除去對角線x=y1=···=ym上的局部可積函數(shù),如果K 滿足以下三個(gè)條件: (i)存在一個(gè)常數(shù)A>0,使得對任意x 與y1,...,ym不全等的(x,y1,···,ym)∈(Rn)m+1都有 則稱K 為Dini 型m-線性Calderón-Zygmund 核. 定義2[11]設(shè)T :S(Rn)×···×S(Rn)→S′(Rn),如果滿足以下兩個(gè)條件: (i)存在一個(gè)Dini 型m-線性Calderón-Zygmund 核K,使得 (ii)存在1 ≤q1,···,qm<∞ 且使得T 是從Lq1×···×Lqm到Lq上的有界算子,則稱T 為帶Dini 核的m-線性Calderón-Zygmund 算子,簡記T ∈ ω-CZO. 顯然地,對某個(gè) ε > 0,當(dāng) ω(t) = tε時(shí),ω-CZO 為Grafakos 和Torres 在文獻(xiàn)[4]中所研究的經(jīng)典多線性Calderón-Zygmund 算子. 2009 年,Maldonado 和Naibo 在文獻(xiàn)[10]中證明了T 為帶Dini 核的雙線性Calderón-Zygmund 算子,在 ω 是凹函數(shù)且ω ∈Dini(1/2)的條件下,算子T 在乘積Lebesgue 空間上是有界的.2014 年,Lu 和Zhang在文獻(xiàn)[11]中將Maldonado 和Naibo 的結(jié)果推廣到多線性情形,同時(shí)削弱了ω 的條件,只需要ω ∈Dini(1).值得注意的是,Lu和Zhang在文獻(xiàn)[11]中也做了BMO 線性交換子的結(jié)果,但由于交換子相對算子本身有更多的奇性,對于ω 需要如下的更強(qiáng)的條件: 最近,Zhang 和Sun 在文獻(xiàn)[13]中考慮了迭代交換子的情形.設(shè)且 ω 滿足 如果1 定義3[14]設(shè)0<β<1,給出Lipβ(Rn)的定義為 2009 年,王偉和徐景實(shí)在文獻(xiàn)[14]中研究了多線性Calderón-Zygmund 算子與Lipschitz 函數(shù)生成的交換子在乘積Lebesgue 空間上的有界性. 受上述工作啟發(fā),一個(gè)自然的問題是:帶Dini 核的多線性Calderón-Zygmund 算子與Lipschitz 函數(shù)生成的迭代交換子在乘積Lebesgue 空間上是否有界?注意到,由于Lipschitz 函數(shù)的特殊性,本文將文獻(xiàn)[13]中BMO交換子的結(jié)果做到Lipschitz 交換子時(shí),對ω 滿足的條件,可以削弱為ω ∈Dini(1). 定理1設(shè)1 便于行文,我們給出一些必要的記號(hào)和說明:aB,a>0,表示與球B 同中心,邊長伸縮a 倍的球體;C 表示與主要指標(biāo)無關(guān)的常數(shù),每次出現(xiàn)時(shí)其值可能并不相同; 對于Rn中的可測子集E,用χE表示E 的特征函數(shù),對1 ≤p ≤∞,p′為p 的共軛指標(biāo),即滿足 我們首先引入一些相關(guān)的定義和結(jié)果. 定義4[15]設(shè)Sharp 極大函數(shù)M?f 的定義為 其中Q 為Rn中包含x 的方體. 對于0 定義5[14]對非中心極大算子的定義為 引理1[17]若0<β<1,1 ≤p<∞,則有 引理2[17]設(shè)0<β<1,f ∈Lipβ,Q1,Q2為Rn中任意兩個(gè)方體.若Q1?Q2,則有 定理證明中,我們將多次使用如下的Kolmogorov 不等式. 設(shè)0 為了證明本文的主要定理,需要給出一個(gè)關(guān)鍵的Sharp 極大函數(shù)估計(jì),即引理3.這一方法可以在文獻(xiàn)[6]中找到.不失一般性,我們只證明m=2 的情形,即考慮 引理3設(shè)0<β1,β2<1,b1∈Lipβ1,b2∈Lipβ2,T ∈ ω-CZO,且 ω ∈Dini(1).如果且p1,p2>1,那么存在一個(gè)常數(shù)C>0,使得對有 其中 證明固定x ∈Rn,Q 為Rn中包含x 的方體.對于a,b ∈R,0 因此,為了證明(1)式,只需證明 對 ?λ1,λ2∈R,z ∈Rn,有 進(jìn)而可得 從而有 其中 II,III 和IV 類似. 下述證明過程中,取λi=(bi)Q,i=1,2. 首先估計(jì)I,由H?lder 不等式及引理2,可得 下面估計(jì)II,由H?lder 不等式及引理2,可得 類似于II 的估計(jì),可得 最后,估計(jì)IV. 其中 進(jìn)一步地有 首先估計(jì)IV1,由Kolmogorov 不等式,算子T 的有界性,引理2及對指標(biāo)p1,p2>1 分別運(yùn)用H?lder 不等式,可得 對于x,z ∈Q,y ∈RnQ?,易知|x?y|≈|z ?y|. 接下來估計(jì)IV2,由核K 滿足的條件,引理2,引理3 及對指標(biāo)p1,p2>1 分別運(yùn)用H?lder 不等式,可得 對于IV3這一部分,類似于IV2的估計(jì),可得 最后估計(jì)IV4,取對于0<δ<1,由H?lder 不等式知 注意到,對任意x,z ∈Q 和任意y1,y2∈?k,有 則由ω 是非減函數(shù),且由核K 滿足的條件,可得 進(jìn)而由引理3,ω ∈Dini(1)及對指標(biāo)p1,p2>1 分別運(yùn)用H?lder 不等式,可得 綜合以上估計(jì),即證明了(1)式.類似地,可以證明(2)和(3)式,這樣便完成了引理3 的證明. 定理1 的證明:對中稠密,因此只需證明對成立即可. 根據(jù)引理3 及Fefferman-Stein 不等式,可得 對于1 < q1,q2< ∞,可以選擇引理3 中的p1,p2,使得1 < p1< q1,且1 < p2< q2.令由則有 從而有 類似地,我們有 和 從而有 這樣便完成了定理1的證明. 注:在運(yùn)用Fefferman-Stein 不等式時(shí),需要在不等式左邊小于無窮的條件下,這一部分內(nèi)容可以參看文獻(xiàn)[6].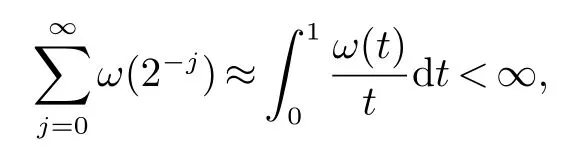

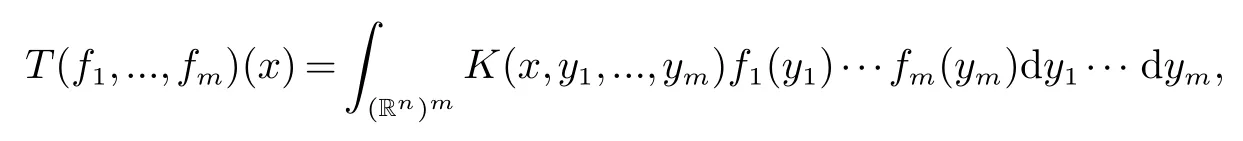
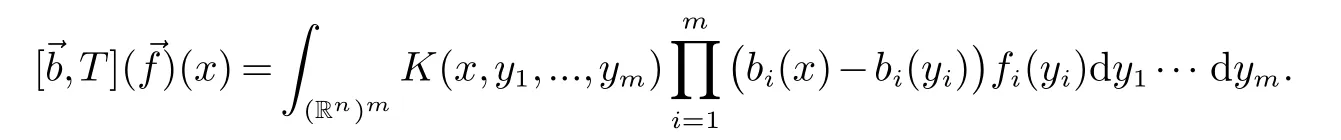

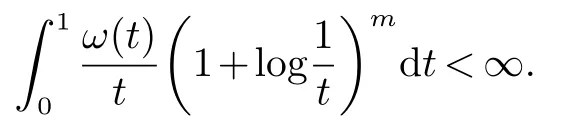
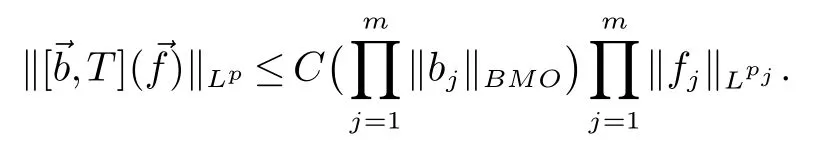
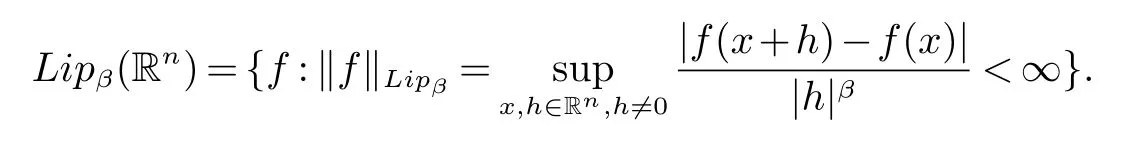
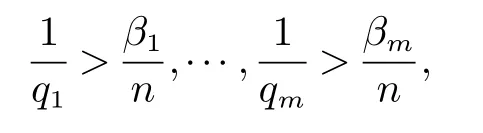
1 預(yù)備知識(shí)
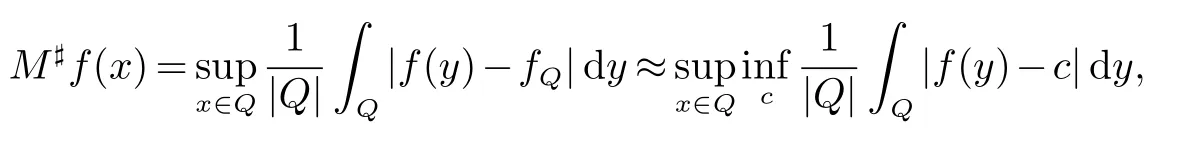
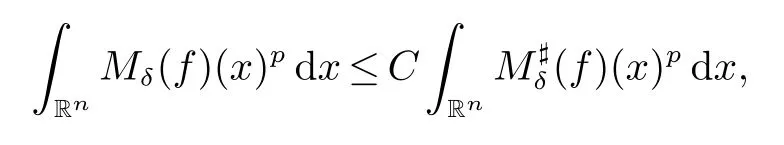
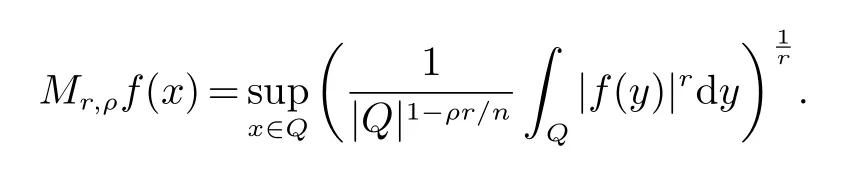
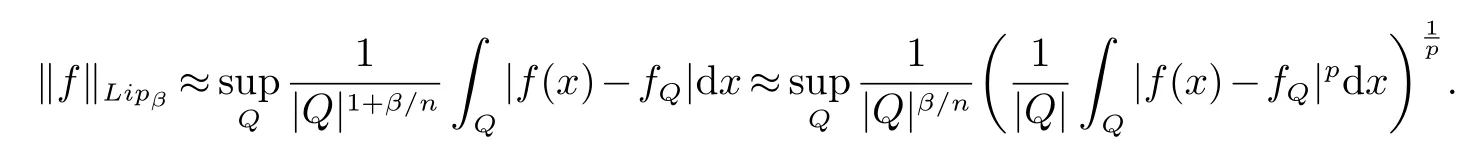


2 主要結(jié)果及其證明

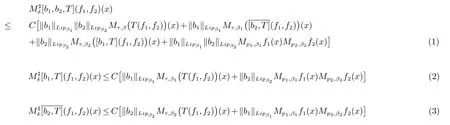
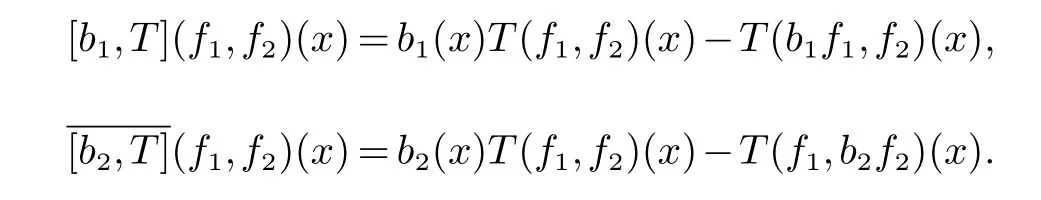

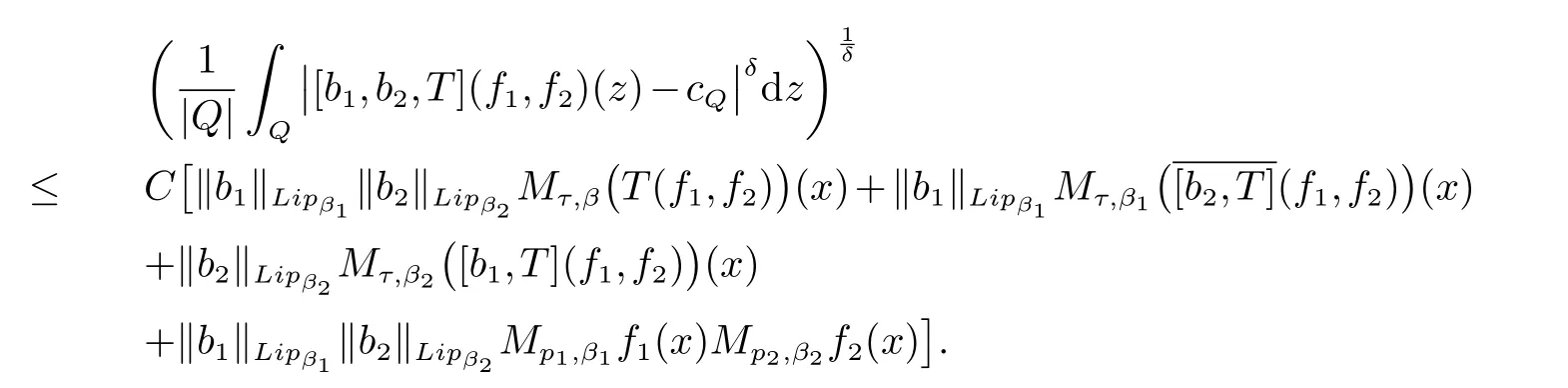
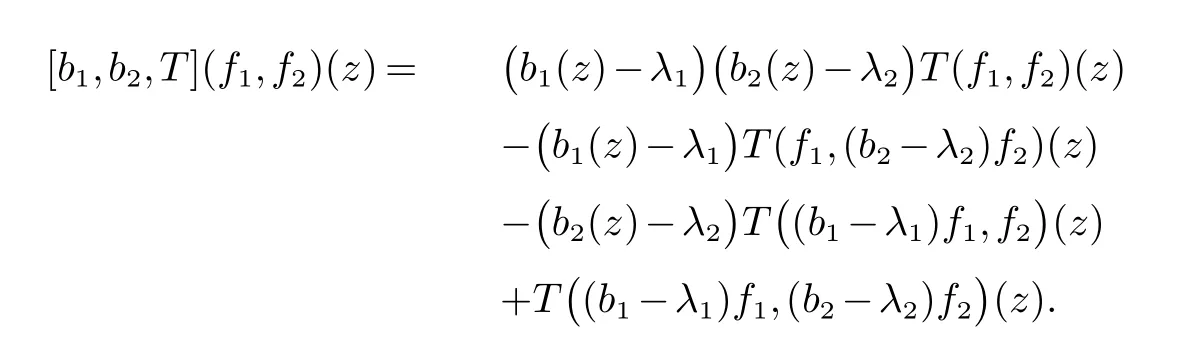
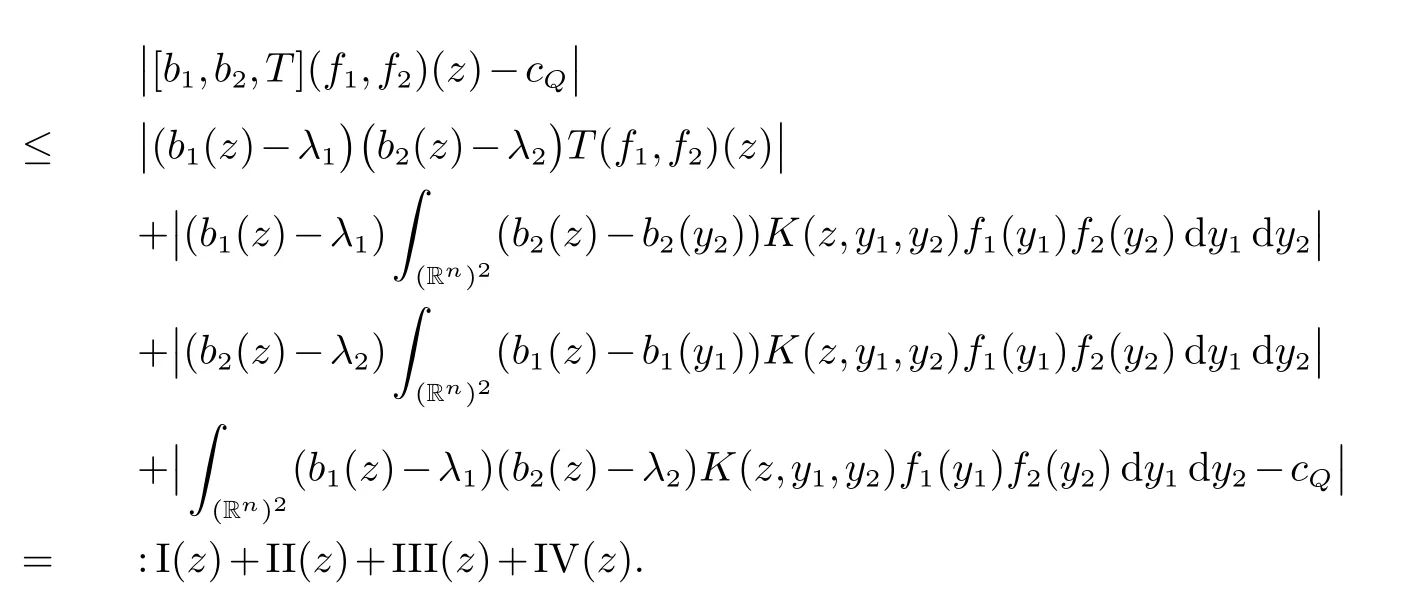
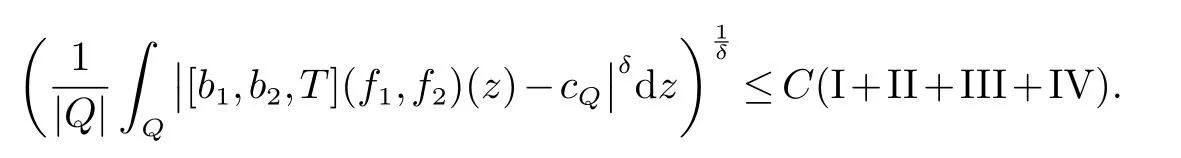
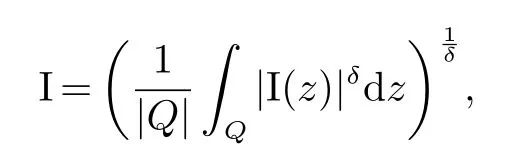
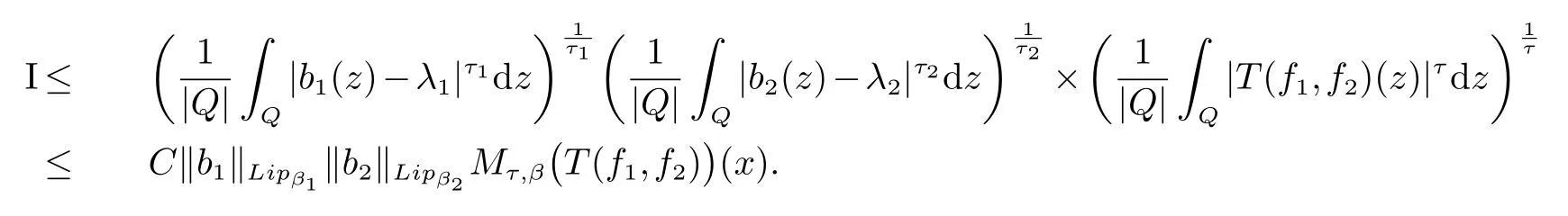
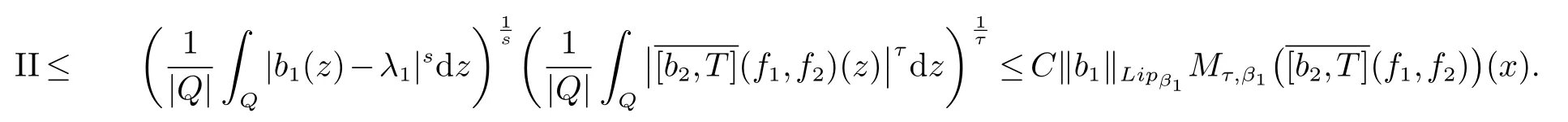

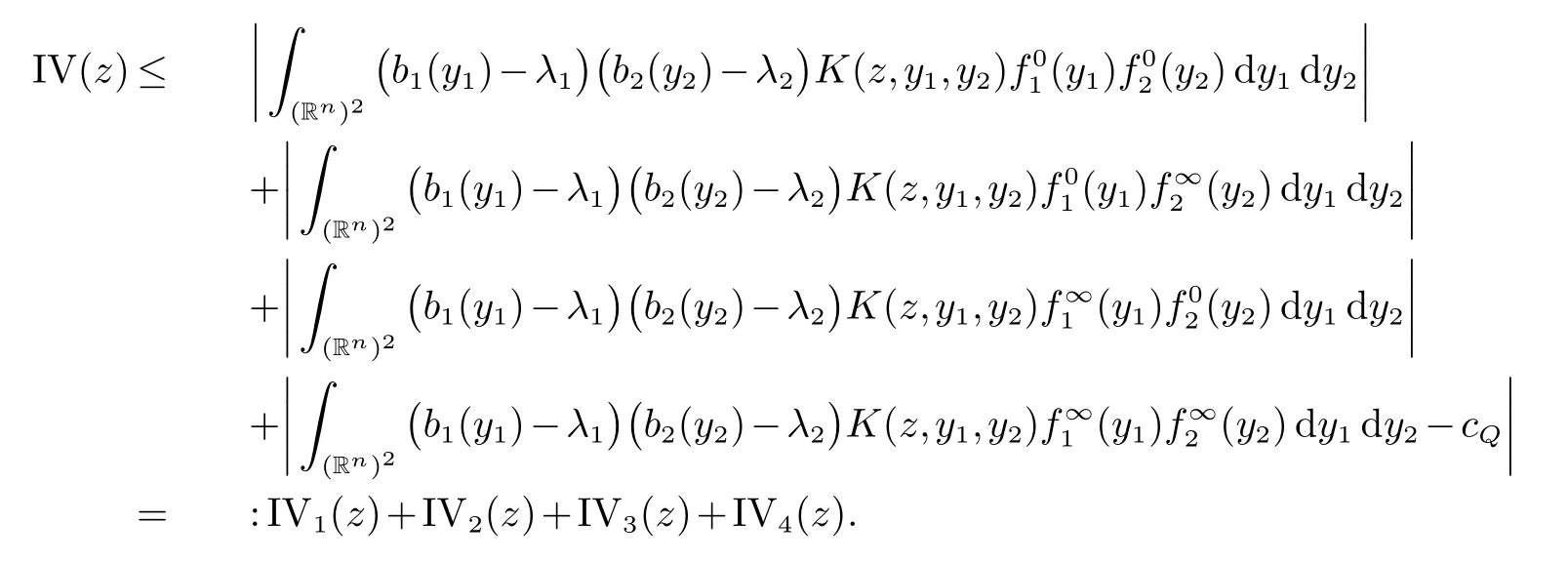
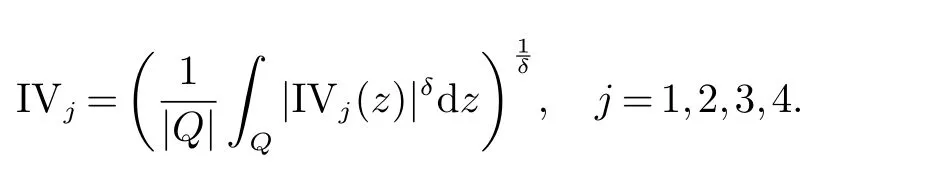
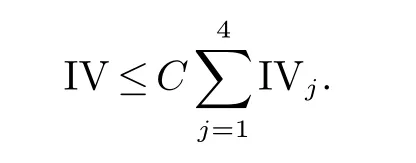

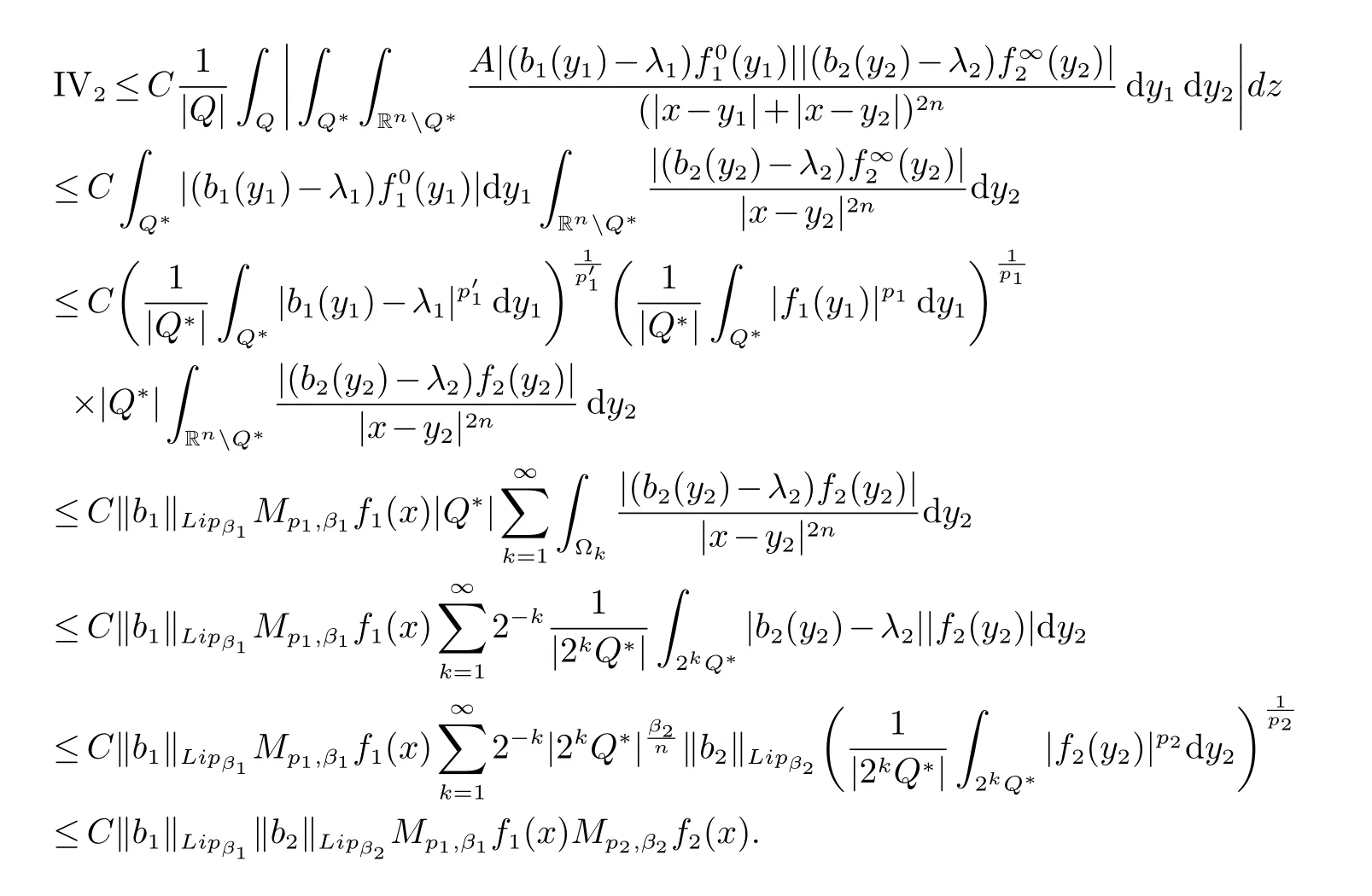
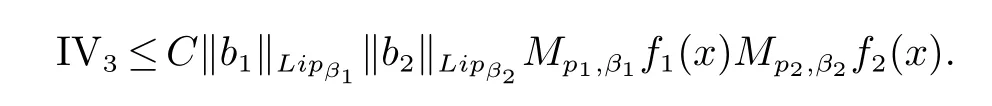
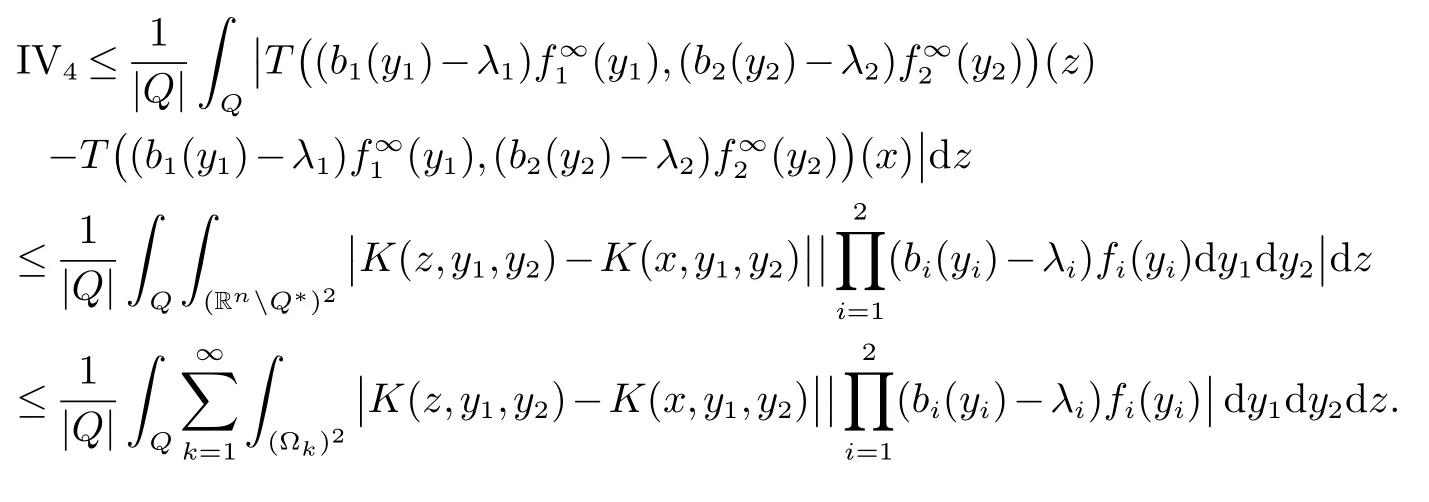
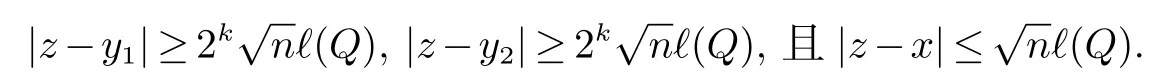
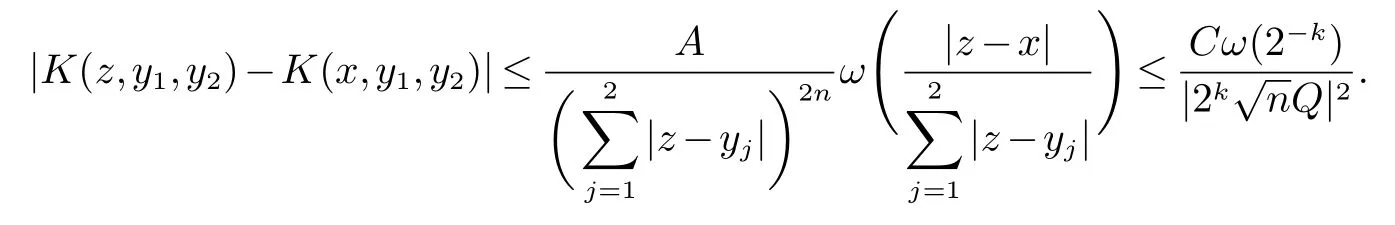
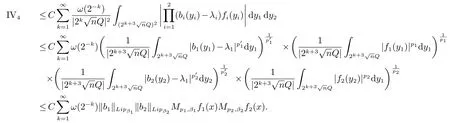
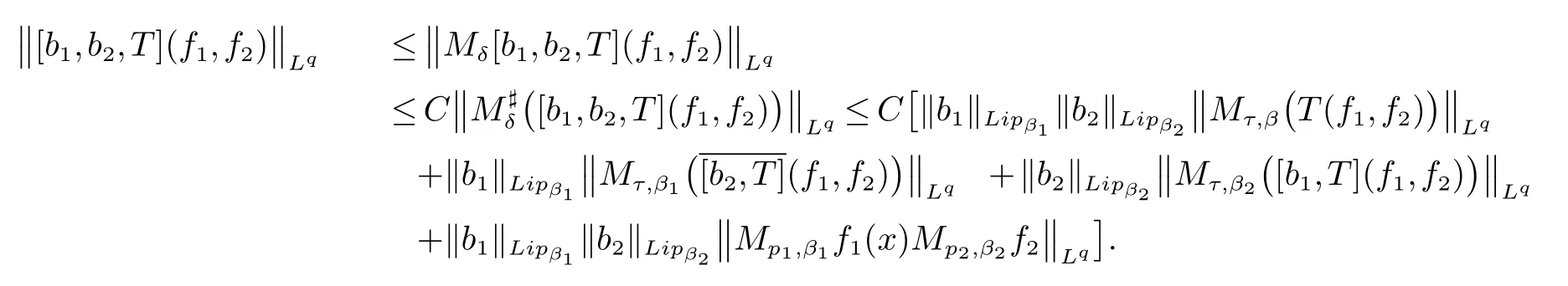
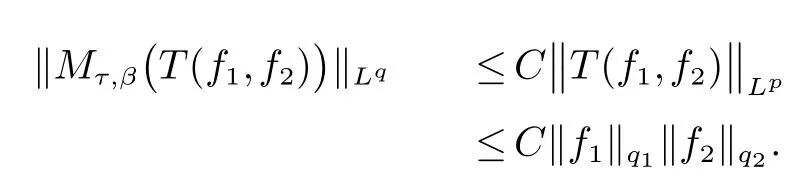
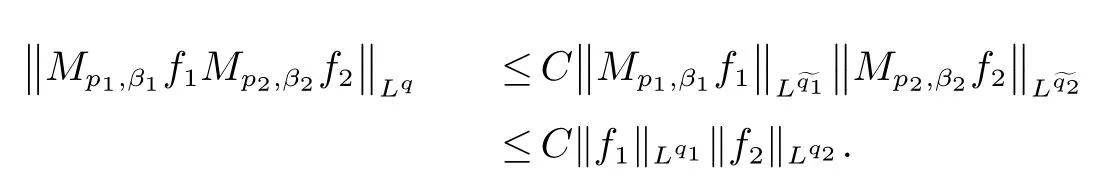
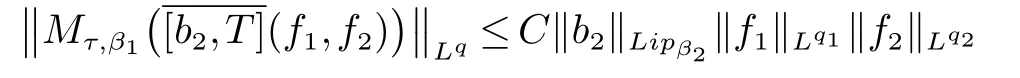
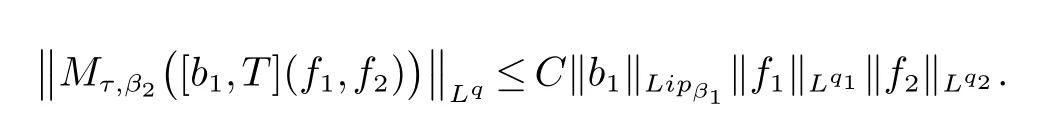

 新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)2019年4期
新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)2019年4期
