何桂添李科宇唐國吉

(廣西民族大學(xué) 理學(xué)院,廣西 南寧530006)

0 引言

連續(xù)性是函數(shù)的基本概念.二元函數(shù)是多元函數(shù)最簡單的情形,國內(nèi)現(xiàn)行的數(shù)學(xué)分析教材幾乎都包含二元函數(shù)連續(xù)性這部分內(nèi)容.[1-3]如參見方麗菁等[4]進一步研究了二元函數(shù)的連續(xù)與關(guān)于單變量連續(xù)之間的關(guān)系,獲得了一些新的結(jié)果.

受以上文獻的啟發(fā),我們繼續(xù)探討二元函數(shù)的連續(xù)性.引入二元函數(shù)的相對連續(xù)性概念.通過例子,我們知道二元函數(shù)的相對連續(xù)性嚴格弱于它的連續(xù)性,且包含二元函數(shù)的關(guān)于單變量連續(xù)作為特例.研究了相對連續(xù)的二元函數(shù)的局部性質(zhì)和整體性質(zhì).作為介值性的應(yīng)用,考察了二重積分的中值定理.推廣和改善了一些已知的結(jié)果.

1 定義

定義1 設(shè)c是包含于平面點D?R2的一條曲線段,設(shè)f定義在點集D上的二元函數(shù),點P0(x0,y0)∈c.

(i)稱f關(guān)于集合D在點P0連續(xù),如果對于任給的正數(shù)ε,總存在相應(yīng)的正數(shù)δ,只要P∈U(P0;δ)∩D,就有

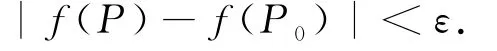
(ii)稱f關(guān)于集合D在點P0相對于曲線段c連續(xù),如果對于任給的正數(shù)ε,總存在相應(yīng)的正數(shù)δ,只要P∈c：l c(P,P0)＜δ,就有

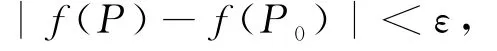
其中l(wèi) c(P,P0)表示沿曲線c點P到點P0的弧長.

(iii)稱f關(guān)于集合D在點P0對變量x連續(xù),如果對于任給的正數(shù)ε,總存在相應(yīng)的正數(shù)δ,只要P(x.y0)∈D：|x-x0|＜δ,就有

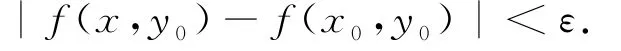
類似地,可定義f關(guān)于集合D在點P0對變量y連續(xù).

注1：定義1中,條目(i)和(iii)是熟知的,可參考文[1,2],條目(ii)由本文給出.按極限定義,f關(guān)于集合D在點P0連續(xù)等價于等價于f關(guān)于集合D在點P0對變量x連續(xù)等價于f(P0);f關(guān)于集合D在點P0相對于曲線段c連續(xù)

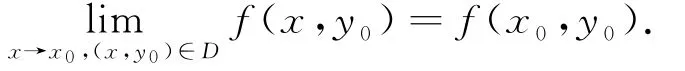
注2：當D=c時,定義1中的條目(i)和(ii)等價.一般地,定義1中的(i)蘊含(ii).方便起見,我們可以表述為：f在點P0連續(xù)蘊含相對連續(xù).反之不然,參看下面的例子.

例1 定義二元函數(shù)

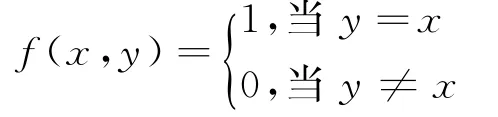
方便起見,記y=x為c.

注3：當c=D∩{(x,y0)|x∈R}時,f在點P0相對于曲線c段連續(xù)退化為對變量x連續(xù);當c=D∩{(x0,y)|y∈R}時,f在點P0相對于曲線段c連續(xù)退化為對變量y連續(xù).也就是說,f在點P0相對連續(xù)包含關(guān)于單變量連續(xù)作為特例.

注4：(i)一個二元函數(shù)關(guān)于某曲線段c的相對連續(xù)點必落在該曲線段c上.

(ii)存在二元函數(shù)f,使得它在除去某曲線段c以外的點都是間斷點,而曲線段c上的點不僅是f相對于c連續(xù)的點,而且還是f的連續(xù)點.

例2 定義二元函數(shù)

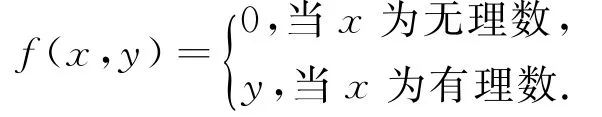
設(shè)(x0,y0)∈R2,則

(a)當x0是有理數(shù)時,

(b)當x0是無理數(shù)時,

2 相對連續(xù)函數(shù)的性質(zhì)

2.1 局部性質(zhì)

若二元函數(shù)在某一點相對于某曲線段連續(xù),則與連續(xù)的二元函數(shù)相類似,可以證明它在這一點沿曲線段的近旁具有一些局部性質(zhì).我們只以局部保號性為例證明,其余略.

定理1(局部保號性) 若二元函數(shù)f在點P0(x0,y0)相對于曲線段c連續(xù),且f(x0,y0)＞0(或f(x0,y0)＜0),則對任何正數(shù)r＜f(x0,y0)(或r＜-f(x0,y0)),存在正數(shù)δ,使得對一切點P(x,y)∈c：l c(P,P0)＜δ,有f(x,y)＞r(或f(x,y)＜-r).

證明：只證明f(x0,y0)＞0的情形,f(x0,y0)＜0的情形可類似證明.取ε=f(x0,y0)-r,由f在點P0(x0,y0)相對于曲線段c連續(xù),根據(jù)定義1(ii)知,存在δ＞0,只要P(x,y)∈c：l c(P,P0)＜δ,就有|f(x,y)-f(x0,y0)|＜ε=f(x0,y0)-r,整理后可得f(x,y)＞r.證完.

定理2(局部有界性) 若二元函數(shù)f在點P0(x0,y0)相對于曲線段c連續(xù),則存在正數(shù)δ,使得f在{P(x,y)∈c：l c(P,P0)＜δ}上有界.

定理3(四則運算法則) 若二元函數(shù)f,g在點P0(x0,y0)相對于曲線段c連續(xù),則它們的和,差,積,商函數(shù)

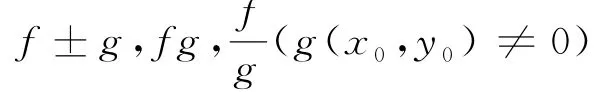
在點P0(x0,y0)也相對于曲線段c連續(xù).

2.2 整體性質(zhì)

定理4(有界性與最值性) 設(shè)c是區(qū)域D中的有限長閉曲線段(即包含端點),若f在c上相對于c連續(xù),則

(i)f在c上有界;

(ii)f在c上能取到最大值和最小值.

證明：(i)假設(shè)f在c上無界,則對每個正整數(shù)n,必存在P n∈c,使得

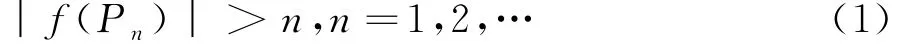
由c是有限長的可推知﹛P n﹜是一個有界無限點列,由聚點定理知,﹛P n﹜存在收斂子列﹛P n k﹜,設(shè).因為c是閉曲線段,所以P0∈c.由于f在c上相對于c連續(xù),當然在點P0也相對于c連續(xù),所以.這與不等式(1)矛盾.

注5：我們發(fā)現(xiàn),定理4的結(jié)論及證明過程與文[1]的定理16.8無原則性變化.注2已經(jīng)指出：當D=c時,定義1中的(i)和(ii)等價.因此定理4的條件完全可以理解為：f在有界閉集c上連續(xù).文[1]112頁指出：文[1]的定理16.8和定理16.9中的有界閉域可以改為有界閉集(證明過程無原則性變化).這樣,定理4的結(jié)論成立.完全類似地,有相應(yīng)的一致相對連續(xù)性定理.

定理5(一致相對連續(xù)性) 設(shè)c是區(qū)域D中的有限長閉曲線段,若f在c上相對于c連續(xù),則f在c上一致相對于c連續(xù).即對任意的正數(shù)ε,存在正數(shù)δ,使得任意的點P,Q∈c∶l c(P,Q)＜δ,有│f(P)-f(Q)│ ＜ε.

定理6(介值性) 設(shè)c是區(qū)域D中的有限長閉曲線段,若f在c上相對于c連續(xù),若P1,P2為c上任意兩點且f(P1)＜f(P2),則對任意μ∶f(P1)＜μ＜f(P2),必存在點P0∈c,使得f(P0)=μ.

證明：作輔助函數(shù)

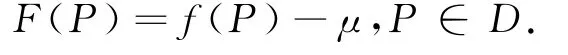
由定理3知,F在c上也相對于c連續(xù).易知F(P1)＜0,F(P2)＞0.設(shè)曲線段c(P1,P2)(即曲線段c中以P1,P2為端點的那一個子曲線段)的參數(shù)方程是

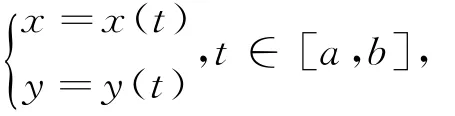
其中參數(shù)a對應(yīng)點P1,參數(shù)b對應(yīng)點P2.令

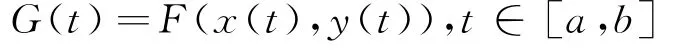
它是[a,b]上的一元連續(xù)函數(shù),且F(P1)=G(a)＜0＜G(b)=F(P2).由一元函數(shù)根的存在性定理知,在(a,b)內(nèi)存在一點t0,使得G(t0)=0.記x0=x(t0),y0=y(t0).則有P0(x0,y0)∈c使得F(P0)=G(t0)=0,即f(P0)=μ.證完.

注6：注2已經(jīng)指出,f在區(qū)域D上連續(xù)蘊含著f在c上相對于c連續(xù),反之不然.因此與文[1]定理16.10相比較,我們把定理的條件從連續(xù)性減弱為相對連續(xù)性.

3 應(yīng)用

定理7(二重積分中值定理) 如果二元函數(shù)f滿足以下條件：

(i)f在有界閉區(qū)域D上可積(二重積分);

(ii)f在P1,P2∈D分別取到最小值m和最大值M,且存在聯(lián)結(jié)P1和P2的有限長曲線段c?D,使得f在c上相對于c連續(xù),那么存在點(ξ,η)∈c,使得

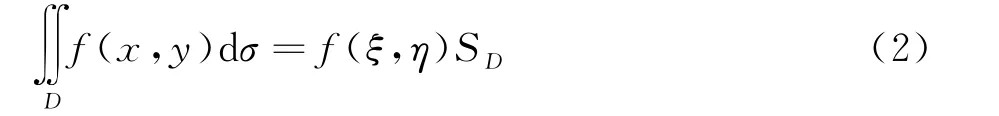
這里S D表示積分區(qū)域D的面積.

證明：由條件(ii)可知,

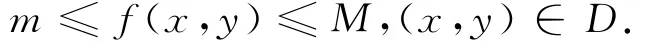
由條件(i)并利用積分不等式性質(zhì)得到

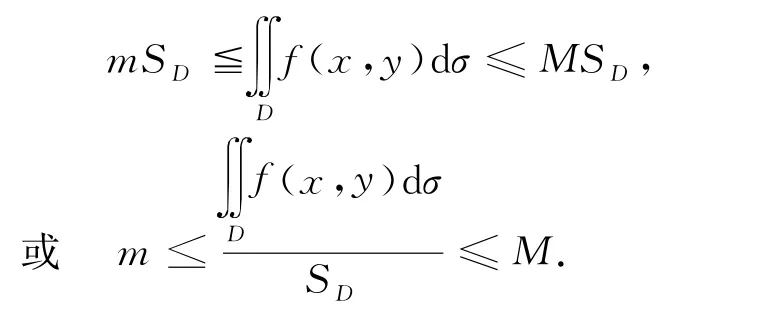
由定理6知,至少存在一點(ξ,η)∈c,使得這就證得(2)成立.證完.

注7：文[1]229頁二重積分中值定理要求二元函數(shù)f在有界閉區(qū)域D上連續(xù),我們的組合條件(i)和(ii)嚴格弱于連續(xù)性條件.參看下例.

例3 設(shè)D=[-1,1]×[-1,1].定義二元函數(shù)

易知f在D上不連續(xù),故文[1]229頁二重積分中值定理失效.而由二重積分的幾何意義,易知f在D上可積,有在點P1(0,-1)和P2(0,1)分別取到區(qū)域D上的最小值0和最大值2.記c=﹛(x,y)∈D∶x=0﹜,f在c上相對于c連續(xù).故定理7的兩個條件滿足,可推知存在一點(ξ,η)∈c使得.事 實 上,取.從而有