Hong-Chen Fu(付洪忱) and Zhi-Rui Gong(龔志瑞)

College of Physics and Optoelectronics,Shenzhen University,Shenzhen 518060,China

(Received June 4,2019;revised manuscript received June 9,2019)

AbstractNon-Markovian master equation of Harmonic oscillator and two-level systems are investigated using the hyper-operator approach.Exact solution of time evolution operator of Harmonic oscillator is obtained exactly.For two-level system the time evolution operator is exactly found and coefficients satisfy ordinary differential equation.

Key words:Non-Markovian approximation,master equation,hyper-operators

1 Introduction

Quantum systems in heat bath follow the master equations.[1?2]Usually only the weak system-environment coupling regime is considered.In this case the Markovian approximation is used and the system is described by the master equation,in which the decay coefficient does not depend on time.[3?4]For the simplest systems such as harmonic oscillator and two-level system,the master equations can be solved using different methods under the Markovian approximation.

Beyond the Markovian approximation,the non-Markovian dynamics of open systems are investigated in the past few years.[5?20]In this case,the decay coefficient is no longer time-independent,rather it is a function of time t.[21?23]Such master equation is well studied for different systems.It seems that there is not an exact solution yet for this kind system.

In this paper we shall investigate the exact solution of harmonic oscillator and two-level system for the non-Markovian process.The exact solutions are achieved by making use of the hyper-operator techniques[24]and Wei-Norman theorem[25]for the harmonic oscillator system and two-level system.Harmonic system is solved exactly for any time-dependent decay coefficient and two-level system is determined by the second-order differential equation.We hope that this approach can help us to understand the decay process of quantum systems beyond the Markovian approximation.

This paper is organized as follows.In Sec.2,we investigate the exact solution of the time evolution of the harmonic oscillator in a heat bath beyond the Markovian approximation.The time evolution operator of the two level system is exactly found in Sec.3.We conclude in Sec.4.

2 Harmonic oscillator in heat bath

Consider a Harmonic oscillator in heat bath

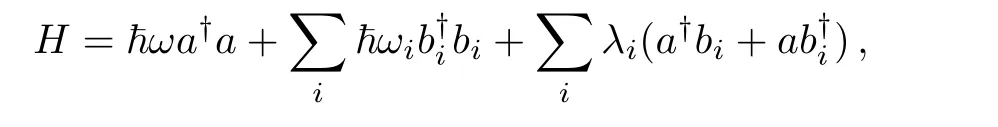
where a,a?are annihilation and creation operators of harmonic oscillator and bi,b?iare annihilation and creation operators of heat bath.

Then its master equation is known as[1]

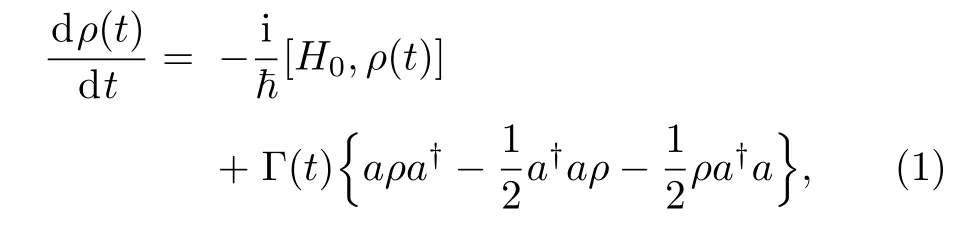
where Γ(t)is time-dependent in general.Under Markovian approximation,Γ(t)is time independent.Changing to interaction picture,we have

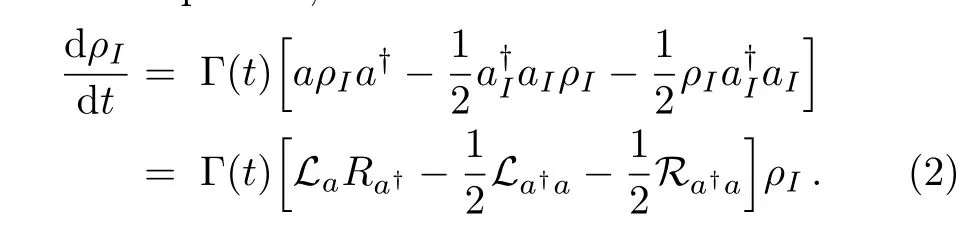
Let V be the Hilbert space of oscillator and End(V)be the linear space of all linear operators on V.Furthermore,all operators on End(V)constitute a linear space End(End(V))and those operators are called hyperoperator.The operators Laand Raetc.introduced in Eq.(2)are hyper-operators acting on ρI∈ EndV,by multiplying a on the left hand side and right hand side,respectively

which are called the left-multiplication and right multiplication hyper-operators,respectively.

In terms of the hyper-operators,the master equation(2)is rewritten as

where

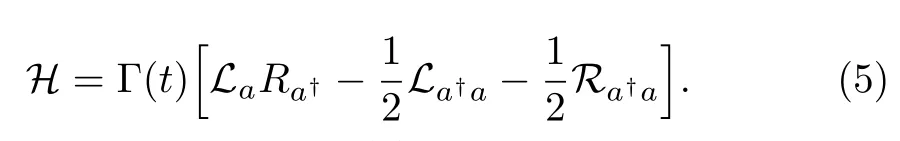
Note that,although Eq.(4)looks like the Schrdinger equation,it is not usual Schrdinger equation.In fact,H is a hyper-operator and ρ∈End(V).Therefore,Eq.(4)can be understood as the Schrdinger equation in EndV and H is the Hamiltonian acting on End(V)rather than V.

Consider the Lie algebra generated by hyper-operators

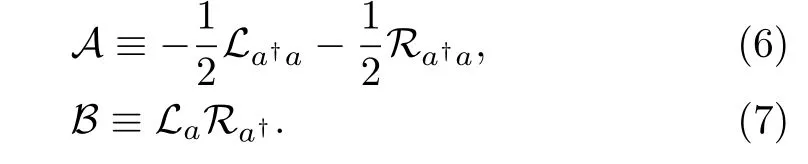
It is easy to see that

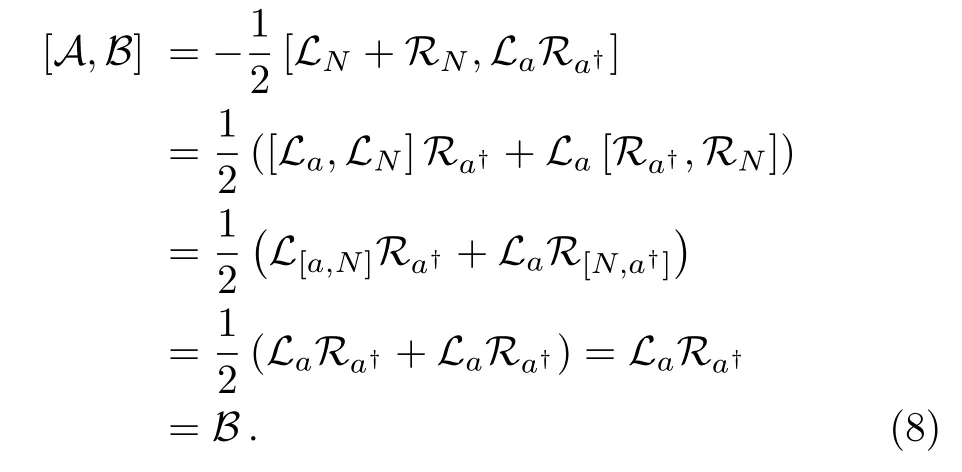
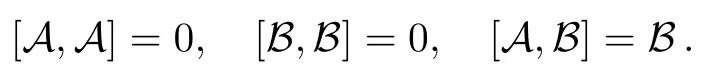
According to Wei-Norman theorem,the time evolution operator U(t)can be written in the form

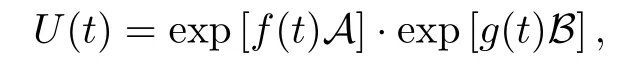
where f(t)and g(t)are time-dependent parameters to be determined.

It is easy to evaluate that

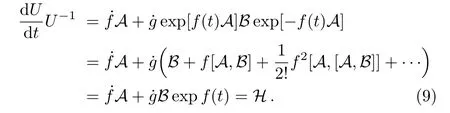
In comparison with Eq.(5),we find

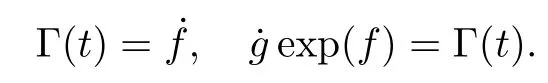
One can easily find the coefficient f(t)from the first equation.Combining the first and the second equations,we can obtainand the coefficient g(t)can be expressed by

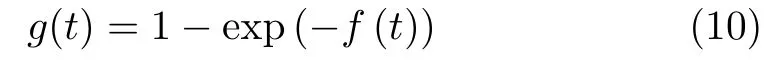
satisfying the initial conditions f(0)=g(t)=0.

For the Markovian approximation,where Γ(t)= Γ is a constant,from Eq.(5),we can directly find that

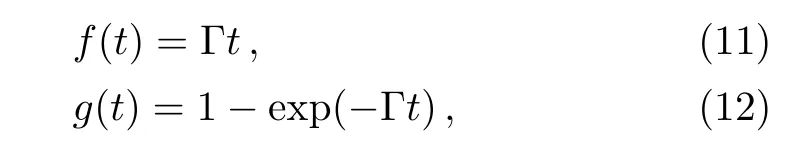
and the time evolution operator is

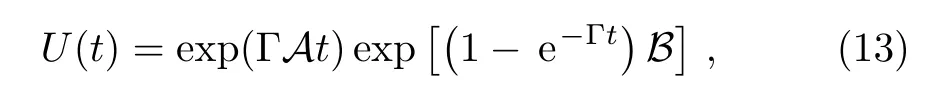
which is a hyper-operator and density matrix at time t is then obtained as

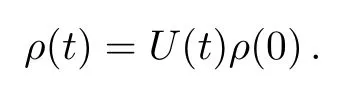
We then obtained the exact solution of harmonic oscillator in the heat bath.

3 Two-level Atom in Heat Bath

Consider a two-level atom in an environment consisting infinite number of harmonic oscillators.The atom can be described by a reduced density operator ρ satisfying the master equation

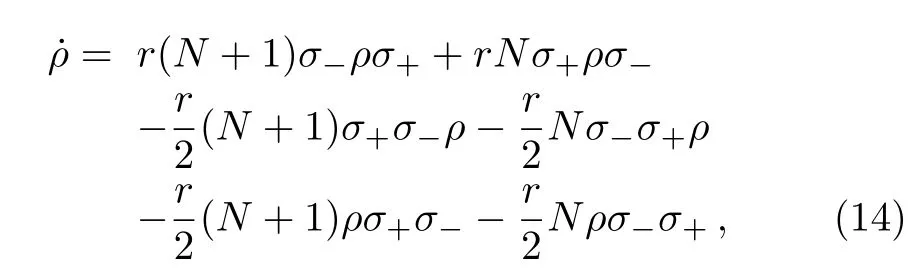
where σ+,σ?are Pauli matrices of two-level atom,r is the time-dependent decay rate and N is the mean number of the bath quanta at the temperature of the heat bath.

We can define the following hyper-operators

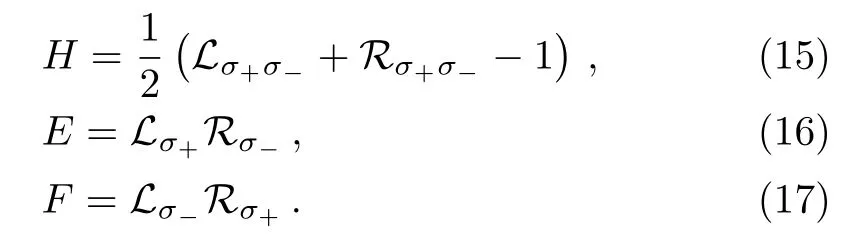
It is easy to prove that those operators satisfy the following communication relations

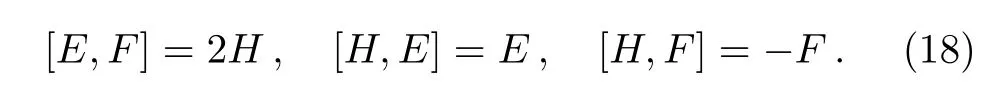
Therefore,Eq.(14)can be rewritten as

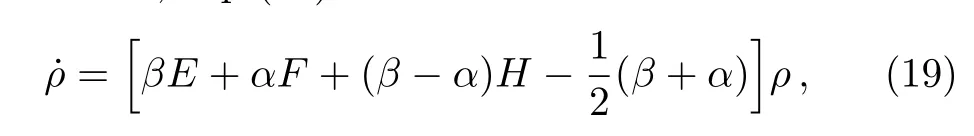
where α and β are

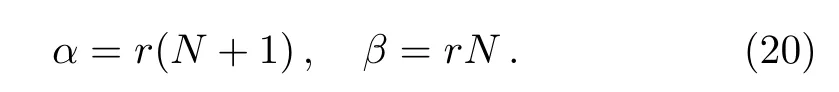
Time evolution operator satisfies the following equation

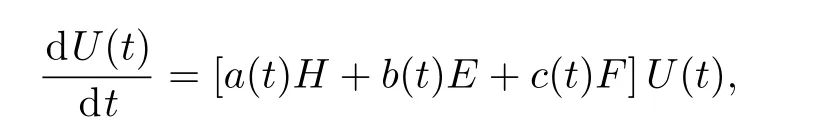
and the time evolution of the density matrix ρ(t)=U(t)ρ(0)with a(t)= β ? α,b(t)= β,and c(t)= α.Write U(t)in the following form

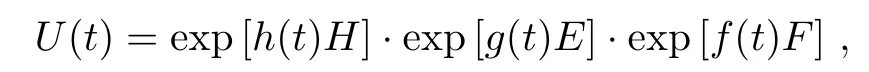
and our aim to find the coefficients a(t),b(t),and c(t).We have

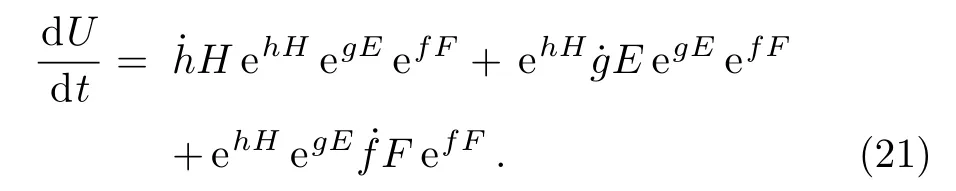
Multiplication of U?1(t)on right side of above equation gives

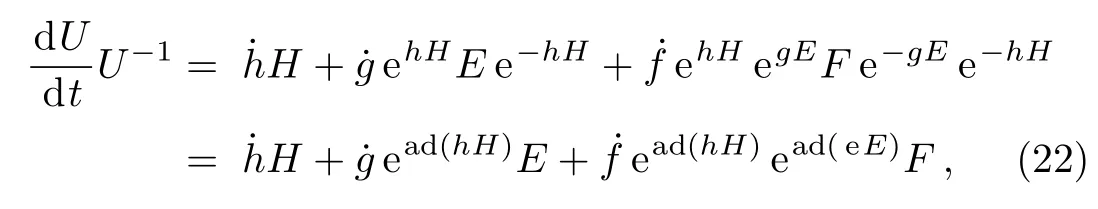
where ad(x)is the adjoint operator defined as

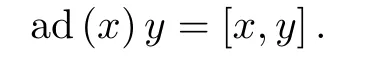
It is easy to find that

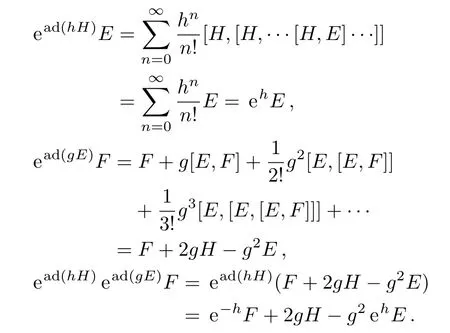
So

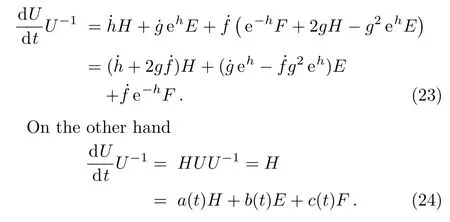
Comparing the coefficients,we find

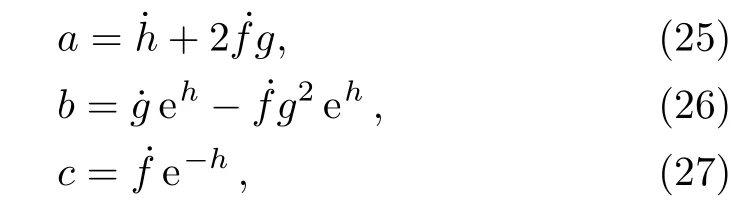
or in the following more elegant form

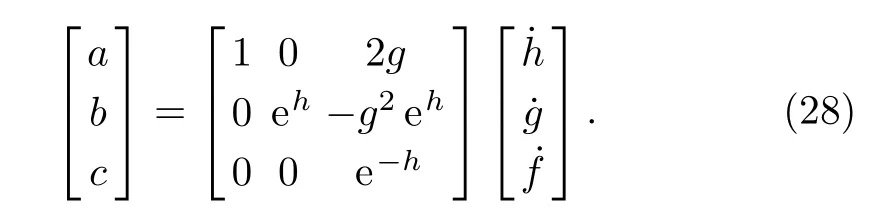
We finally find the relationship between the coefficients in H(t)and that in U(t)

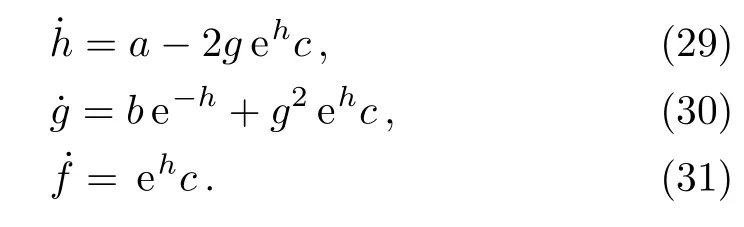
Equations(29)?(31)are nonlinear differential equations and in general they are difficult to be solved.Fortunately,we can change it to the Reccati equation for

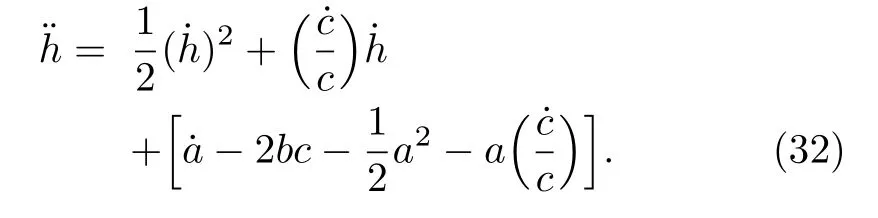
Letting

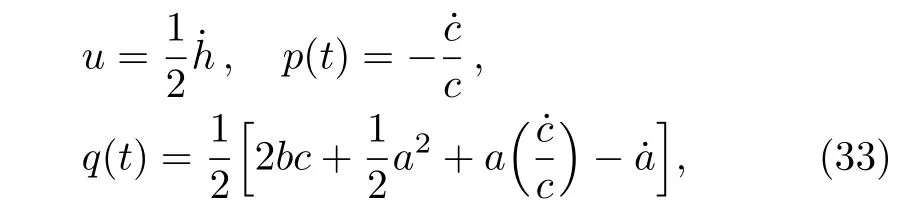
we obtain the Riccati equation satisfied by u=(1/2)˙h and˙u?u2+p(t)u+q(t)=0.Letting u=?v′/v,above equation is further changed to the second-order differential equation

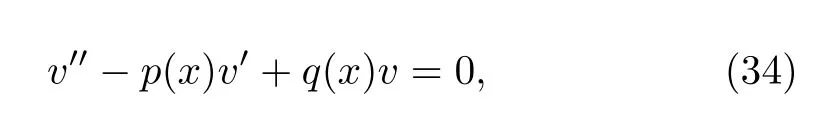
which have been well studied in mathematics.Therefore,solving the master equation of two-level atom reduces to find solutions to Eq.(34).

4 Conclusion

In this paper we investigated solutions to the non-Markovian master equation using Wei-Norman theorem and hyper-operator technique.For harmonic oscillator system,the time evolution operator is exactly derived,and for two-level system the time evolution operator is expressed as linear combination of hyper-operator and the coefficient in the evolution operator can be determined by solving a second-order differential equation.

Appendix A Hyper-operator

Let H be a Hilbert space with dimension N<∞.Then all linear operators on H span an N2-dimensional space End(H).Furthermore,we can consider all linear operators on End(H)which span an N2×N2linear space End(End(H)).We call End(End(H))the Hyper-space and any elements in End(End(H))a hyper-operator.

In the hyper space End(End(H)),one can define the left-multiplication hyper-operator and right multiplication hyper-operator

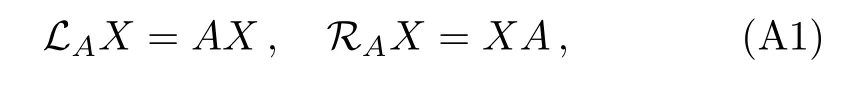
for any X∈End(H).Then one can easily prove that

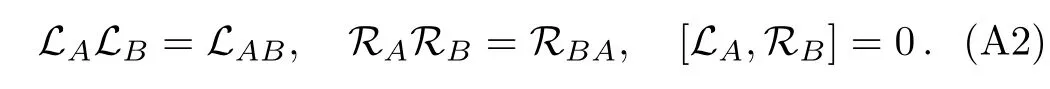
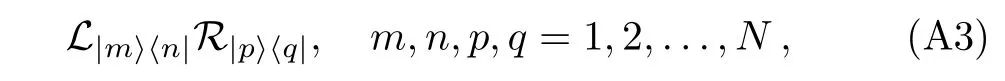
is a basis of End(End(H)).For mathematical details see Ref.[24].