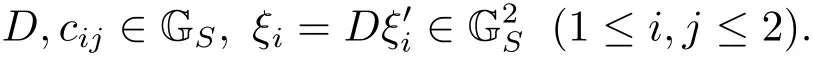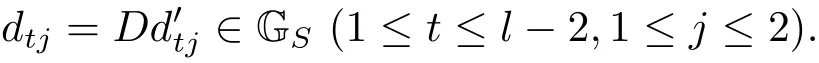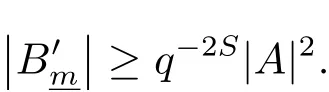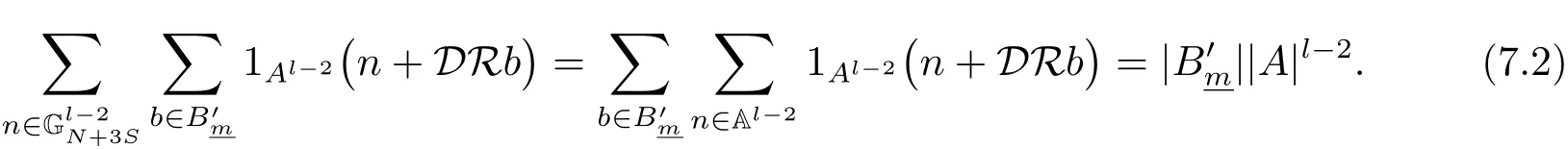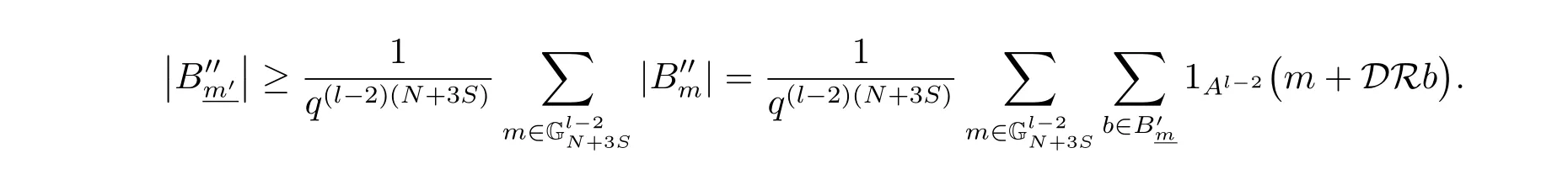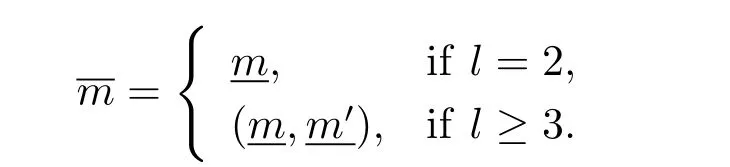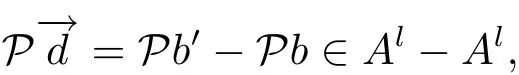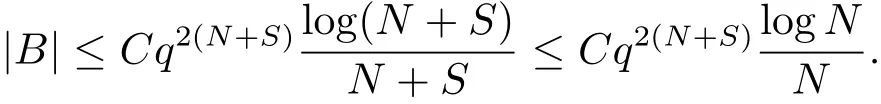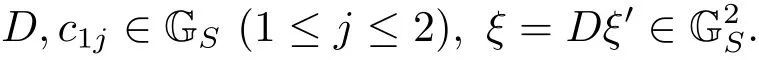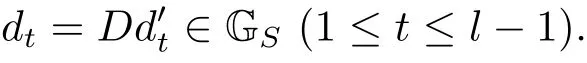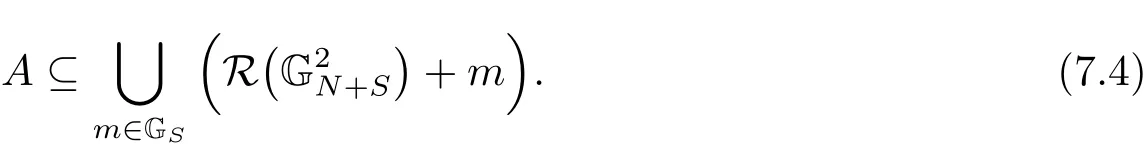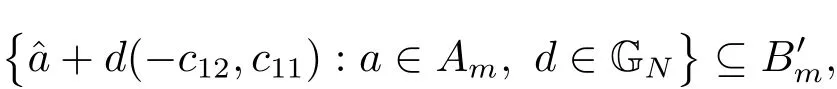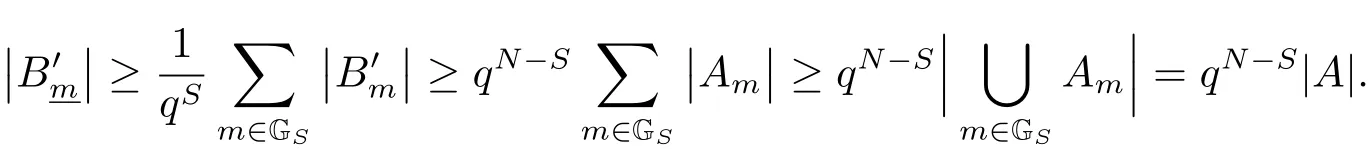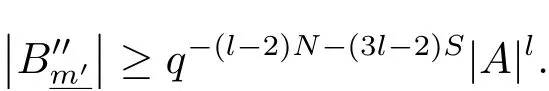A 2-DIMENSIONAL ANALOGUE OF S′ARK?ZY’S THEOREM IN FUNCTION FIELDS
LI Guo-quan, LIU Bao-qing, QIAN Kun, XU Gui-qiao
(School of Mathematics Science, Tianjin Normal University, Tianjin 300387, China)
Abstract: Let Fq[t] be the polynomial ring over the finite field Fq of q elements. For N ∈N,let GN be the set of all polynomials in Fq[t] of degree less than N. Suppose that the characteristic of Fq is greater than 2 and . If (d,∈A ?A= for any d ∈Fq[t]{0},we prove that |A| ≤ where the constant C depends only on q. By using this estimate,we extend S′ark?zy’s theorem in function fields to the case of a finite family of polynomials of degree less than 3.
Keywords: S′ark?zy’s theorem; function fields; Hardy-Littlewood circle method
1 Introduction
Let N={0,1,2,···} and write N+for N{0}. For a subset A of an additive group, we define the difference setIf A also is finite, we denote by |A| its cardinality.
In the late 1970s, Furstenberg [1] and S′ark?zy [2] independently proved the following conclusion. If A is a subset of positive upper density of Z, then there exist two distinct elements of A whose difference is a perfect square. The latter also provided an explicit estimate, but the former result is not quantitative. S′ark?zy’s theorem was later improved by Pintz, Steiger and Szemer′edi in [3], where they obtained the following theorem.
Theorem AThere exists a constant D >0 such that the following holds. Let N ∈N+and A ?N ∩[1,N]. If (A ?A)∩{n2:n ∈N+}=?, then we have

Remark 1Balog, Pelik′an, Pintz and Szemer′edi [4] showed that one may replacebyin the above bound. This estimate is the current best known bound.
In 1996, by extending the ideas of Furstenberg, Bergelson and Leibman [5] established a far reaching qualitative result, the so-called Polynomial Szemer′edi theorem. It is natural to ask for a quantitative version of the Polynomial Szemer′edi theorem. Recently, Lyall and Magyar[6]made some progress towards this problem. They first proved a higher dimensional analogue of S′ark?zy’s theorem.
Theorem BFor k ∈N with k ≥2, there exists a constantsuch that the following holds. LetZ{0}=?, then wehave
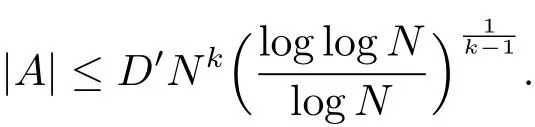
Then by applying Theorem B,they established a quantitative result on the existence of polynomial configurations of the type in the Polynomial Szemer′edi theorem in the difference set of sparse subsets of Z.
Theorem CLet l ∈N+and P1,··· ,Pl∈Z[x]with Pi(0)=0 for i=1,··· ,l.Suppose thatThen there exists a constantsuch that the following inequality holds: let N ∈N+andfor a ny n ∈Z{0}, then we have

Remark 2Theorems B and C were quoted from the revised version of [6], where the authors improved the main results in the original edition.
By taking l=1, P1=x2and k =2, S′ark?zy’s theorem follows from Theorem C. Thus,we may consider Theorem C to be S′ark?zy’s theorem for a family of polynomials.
Let Fqbe the finite field of q elements. Let p denote the characteristic of Fq.We denote by A=Fq[t] the polynomial ring over Fqand write A×=Fq[t]{0}. For N ∈N, let GNbe the set of all polynomials in A of degree less than N.
By adapting part of the Pintz-Steiger-Szemer′edi argument, L?e and Liu [7] obtained an analogue of Theorem A in function fields.
Theorem DIf p ≥3, then there exists a constant, depending only on q, such that the following holds: let N ∈N with N ≥2 and A ?GN.If(A?A)∩{d2:d ∈A×}=?,then we have
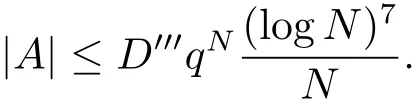
In this paper, for the case k = 2, we consider the analogues of Theorems B and C in function fields. First, by closely following the approach of Lyall and Magyar, which is explained in detail by Rice [8], we prove a 2-dimensional version of S′ark?zy’s theorem in function fields.
Theorem 1If p ≥3,then there exists a constant C >0,depending only on q,such that the following holds: let N ∈N with N ≥2 and. If (A ?A)∩{(d,d2):d ∈A×}=?,then we have
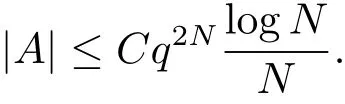
By adapting the lifting argument in [6], we deduce the following analogue of Theorem C from Theorem 1.
Theorem 2Let l ∈N+and P1,··· ,Pl∈A[x] with Pi(0)=0 for i=1,··· ,l. Suppose that≤2 and p ≥3. Then there exists a constantdepending only on q,P1,··· ,Pl, such that the following inequality holds: let N ∈N with N ≥2 and A
In particular,by taking l=1 and P1=x2in Theorem 2,we obtain a slight improvement of Theorem D.
In the general cases k ≥3, it is more difficult to establish a k-dimensional analogue of Theorem B in function fields. The main obstruction is that we are not able to obtain satisfactory exponential sum estimates on the minor arcs (for details of the circle method,see [9]), i.e., suitable generalizations of Proposition 10. We intend to return to this topic in the future.
2 Preliminaries
Let K = Fq(t) be the field of fractions of A. For a,b ∈A with b= 0, we defineThenis a valuation on K. The completion of K with respect to this valuation is K∞=the field of formal Laurent series in.
K∞is a locally compact field and T=is a compact subring of K∞. Let dω be the Haar measure on K∞such that T 1dω =1.
Let tr : Fq→Fpbe the familiar trace map. For c ∈Fq, writ eThe exponential function e : K∞→C×is defined by e(ω) = eq(res ω). Using this function, one can establish Fourier analysis in A. In particular, A,K,K∞,T play the roles of Z,Q,R,R/Z, respectively.
For ω ∈K∞andwrite ωγ = (ωγ1,ωγ2) andLet f,g :A2→C be functions with finite support sets. The Fourier transformC of f is defined byThe convolution f ?g :A2→C of f and g is defined by
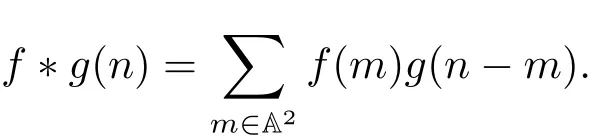
Then it follows that
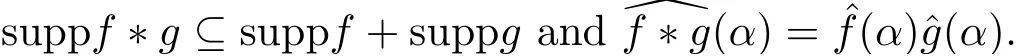
Let dα denote the product of Haar measures. For m ∈A2, we have the orthogonal relation

Lemma 1For M ∈N+and ω ∈K∞, we have

ProofThis is [10, Lemma 7].
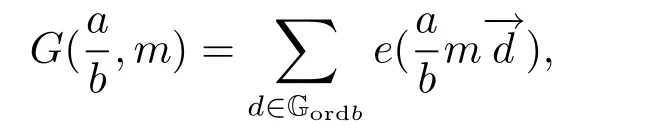
For N ∈N+, the exponential sum SN:T2→C is defined by
Lemma 2Let N ∈N+andgcd(b,m1,m2) = 1. Suppose that ordb
Then we have
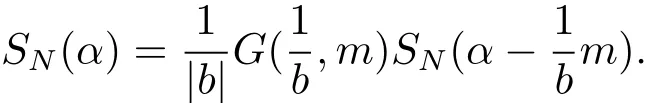
ProofWrite β =(β1,β2)=α ?. Then

Let s ∈GN?ordband t ∈Gordb. Note that

we have e(β1(sb+t))=e(β1sb). Similarly, since
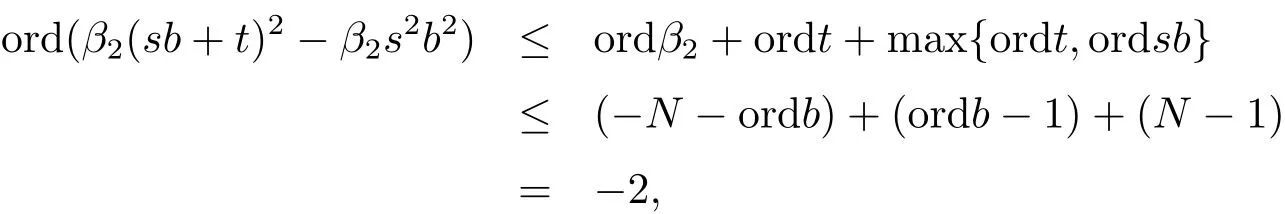
it follows that e(β2(sb+t)2)=e(β2s2b2). Thus, we obtain
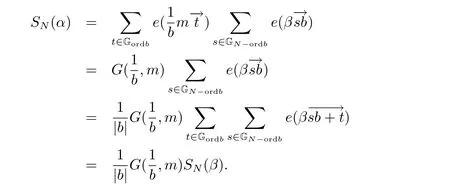
This completes the proof of the lemma.
Lemma 3Let r1,r2∈N.Then for any α=(α1,α2)∈T2,there exists(b,m1,m2)∈A3with the following properties
(i) b is monic and ordb ≤r1+r2;
(ii) gcd(b,m1,m2)=1;
(iii) ordmj ProofFor 1 ≤j ≤2, let Tj=ω ∈T:ordω ≤?rj?1. Then Tjis a subgroup of T.Also, Let c be the leading coefficient ofand letBy taking b =and mj=the lemma follows. In this section, we obtain an estimate forOur arguments run in parallel with the approach of Chen [11]. Lemma 4Let a1,a2,b1,b2∈A with b1,b20 and gcd(b1,a1) = gcd(b2,a2) = 1. Let m=(m1,m2)∈A2. Suppose that gcd(b1,m1,m2)=gcd(b2,m1,m2)=1. If gcd(b1,b2)=1,then ProofSince gcd(b1,b2)=1, b2+b1A is invertible in the ring H1=A/b1A. Thus, Similarly, we have Combining the above two equalities, it follows that Equality (3.1) follows since gcd(b1,b2)=1. Lemma 5Let a,b ∈A withand gcd(b,a)=1. Let m=(m1,m2)∈A2. Suppose that gcd(b,m1,m2)=1. If p ≥3 and b is irreducible, then we have ProofSince b is irreducible and gcd(b,a)=1,it follows that.We divide into two cases. Case 1Suppose that. Since gcd(b,m1,m2)=1,By Lemma 1, we have Case 2Suppose that. Since b is irreducible, H = A/bA is a field. Note thatwe can find an isomorphism T :F|b|→H of fields. Consider ψ :F|b|→C×defined by ψ(c)=e(). It follows from Lemma 1 that Thus, ψ is a non-trivial additive character of F|b|. Let P(t) =. Then P is a polynomial of degree 2 in F|b|[t]. Note that by Weil’s theorem in [12], we have Combining the above two cases, the lemma follows. Lemma 6Let a,b ∈A withand gcd(b,a)=1. Let m=(m1,m2)∈A2. Suppose that gcd(b,m1,m2)=1. If p ≥3 and b is irreducible, then for any r ∈N+, we have ProofWe will prove this lemma by induction on r. For r =1, the lemma follows from Lemma 5. Let r ∈N with r ≥2. Suppose that the lemma holds for allwith. We now prove that the statement is true for r. Note that for d ∈Gordbr, there exist d1∈Gordbr?1and d2∈Gordbsuch that d =This observation allows us to obtain There are two cases. Case 1Suppose that b|m2. Sinceby Lemma 1, we have By (3.2), we have Case 2Suppose thatThen there exists unique d0∈Gordbsuch that For any d1∈Gordbr?1, it follows from Lemma 1 that Write By (3.2), we have If r =2, then If r ≥3, then we deduce from (3.3) that By the induction hypothesis, it follows that By combining the above two cases, we complete the proof of the lemma. Proposition 7Let a,b ∈A withand gcd(b,a) = 1. Let m = (m1,m2) ∈A2.Suppose that gcd(b,m1,m2)=1. If p ≥3, then we have ProofWithout loss of generality, we assume thatand ordb ≥1.Also, b is monic.There exist ι,j1,··· ,jι∈N+and distinct monic irreducible polynomials σ1,··· ,σιin A such thatWe prove the lemma by induction on ι. For ι=1, the lemma follows from Lemma 6. Let ι ∈N with ι ≥2. Suppose that the lemma is true for ι ?1. We now prove that the claim holds for ι. Since gcd(b,a)=1, we can findsuch that By Lemmas 4 and 6, we have By the induction hypothesis, the proposition follows. For the present, we fix N ∈N+and A ?GN×G2Nwith |A|=δq3N. Throughout this section, we assume that the following hypothesis holds. Hypothesis A Take θ ∈N+with q?θ<δ ≤q1?θ. Then N ≥12θ. Write M =N ?6θ. The characteristic function 1A:A2→R of A is defined by Write ΓN= GN×G2N. We define the balanced function fA: A2→R of A to be fA=1A?δ1ΓN. Let b ∈A×with b monic. Write For (a1,a2)∈Ab, we define the Farey arc F(b,a1,a2) to be Also, we define We say F(b,a1,a2) is major if ordb ≤2θ+3 and minor if ordb>2θ+3. Let We define the major arcs M and the minor arcs m as follows: Lemma 8Let b,B. Suppose thatthen we have ProofTo prove the lemma, we suppose the contrary. Then there exists Let 1 ≤j ≤2. Since it follows that It is easy to see that b = lcm(B1,B2) =. It follows that aj=. This leads to a contradiction, and the lemma follows. Proposition 9If b ∈B, then for any α ∈Fb, we have ProofWrite (α1,α2)=α. Take a=(a1,a2)∈Absuch that α ∈F(b,a1,a2). Since by Lemma 2, we have It follows from Proposition 7 that Proposition 10For any α ∈m, we have ProofWrite α = (α1,α2). By using Lemma 3 for r1= 0 and r2= N, we can find a monic polynomial b in A×and a=(a1,a2)∈A2such that ordb ≤N, gcd(b,a1,a2)=1, ordaj In the following, we assume that ordb ≤2θ+3. Consider the following estimate For d ∈GN, since it follows that {β2d}=β2d. By Lemma 1, we have Combining Lemma 2 and Proposition 7 with the above inequality, it follows that Case 1Suppose that |β2|≥q?2M|b|?1. By (4.1), we have Case 2Suppose that If ordβ2≥1 ?N +ordβ1, then by (4.1), we have Thus, it remains to estimate |SN(α)| under the additional assumption ordβ2≤ordβ1?N. Write L1=?ordβ1, then 1 ≤L1≤M+ordb; write L2=?ordβ2, then L2≥1+2M+ordb; writesince L1≤M +2θ+3 For j ∈N, write Cj={d ∈A:ordd=j}, then Let d ∈GK. By the assumption ordβ2≤ordβ1?N, we have It follows that e(β2d2)=1. Note that ord{β1}=?L1≥?K, by Lemma 1, we have Thus Let K ≤I ≤N?1 and d ∈CI.Take c0,c1,··· ,cI∈Fqwithsuch that Then For 0 ≤i,j ≤I, if i+j ≥L2?1, by the assumption ordβ2≤ordβ1?N, we have Thus, there exists the polynomial QI(t1,··· ,tI?L1+1) of (I ?L1+1) variables over Fqsuch that Substituting this into the definition of the functionand noting thatwe have It follows from (4.2) that SN(β)=0. Finally, by Lemma 2, we have SN(α)=0. Combining the above two cases, we complete the proof of the proposition. In this section, we continue to fix N ∈N+and A ?ΓNwith |A| = δq3N. Also, we assume that Hypothesis A holds. Lemma 11 ProofWriteBy (2.1), we have If d ∈GN, then∈ΓN. Thus ΓN+=ΓN?=ΓN. It follows that (A ?A)∩{:d ∈A×}=?from Hypothesis A. Thus Finally, by (5.1) and (5.2), we obtain Lemma 12There exists a monic polynomial b0in G2θ+4such that where 0 ProofBy Proposition 10, we have Write Combining the above inequality with Lemma 11, it follows that For j ∈N, write Oj= {b ∈A×: b monic, ordb = j}. By Lemma 8 and Proposition 9, we have Take a monic polynomial b0in G2θ+4such that It follows from the above inequality that Since δ ≤q1?θ, we can find a constantdepending only on q, such that Lemma 13There exists n0∈ΓNsuch that ProofWrite P =b0ΓM. Let m=(m1,m2)∈ΓMand 1 ≤j ≤2. Since we have b0m ∈ΓN. Thus, P ?ΓN. Also, we have For n ∈ΓN, we have If there exists n0∈ΓNsuch that fA?1?P(n0)≥δ|P|, then Thus, in the following, we assume that fA?1?P(n) ≤δ|P| for all n ∈ΓN. It follows from(5.4) that Let α=(α1,α2)∈Fb0. Take a=(a1,a2)∈Ab0such that α ∈F(b0,a1,a2). Since we have e(b0mjαj)=e(mjaj)=1. Thus,=|P|. It follows from (5.5) that By Lemma 12, we have Take n0∈ΓNsuch that By (5.4), we have Proposition 14There existandwith |such that ProofWrite L = ordb0and T = |b0|. Then 0 ≤L ≤2θ+3. By takingproperty (iii) follows. Take d1,··· ,such that For d ∈GLand 1 ≤i,j ≤T, write where Let m = (m1,m2) ∈ΓM. Take d ∈GLandsuch thatBy(5.6), we can find 1 ≤i,j ≤T such thatThen we have Thus, we see that Take d0∈GLand 1 ≤i0,j0≤T such that By Lemma 13, we have which contradicts Hypothesis A. This completes the proof of the proposition. Proposition 15If p ≥3, then there exists a constant C1> 0, depending only on q,such that the following inequality holds. Let N ∈N with N ≥2 and A ?GN×G2N. If, then we have Remark 3Note that,the form of Proposition 15 is more natural than of Theorem 1. ProofWritethen by taking the proposition follows. Thus in the following, we assume that Now,we recursively define a sequence of triples(Ni,Ai,δi)with Ni∈N+, Ai?ΓNiandδiq3Nias follows. Take (N0,A0,δ0)=(N,A,δ). Let i ∈N. Suppose that (Ni,Ai,δi) is defined. Ifwe stop the definition. If δiby Proposition 14, we can findsuch that Claim 1For j ∈N, write ProofWe prove the claim by induction on j. For j = 0, we haveIt follows from (ii) that Thus if i ≥I0, then δi≥2δ. Suppose that the claim holds for j. We now prove that the statement is true for j+1. This completes the proof of the claim. Take j0∈N such that 2j0δ ≤1<2j0+1δ. Then we have It follows from (iii) that By (6.1), we have Thus, there exists a constant C1>1, depending only on q, such that Note that the function x log x on [1,+∞) is increasing, and the proposition follows since Proof of Theorem 1Write. If N ≤7, by takingthe theorem follows. In the following, we assume that N ≥8. Write For 1 ≤i ≤S and 1 ≤j ≤T, takesuch that Then, we have Write Take 1 ≤i0≤S and 1 ≤j0≤T such that For 1 ≤s ≤l,take cs1,cs2∈A such thatDenote by r the rank of the matrix P. Then 1 ≤r ≤2. Thus, we divide into two case. Case 1Suppose that r =2. Without loss of generality, we assume thatc11,c12andlinearly independent. Writesuch thatWhen l ≥3, takesuch that Take S ∈N with S ≥4 and D ∈A×such that If l ≥3, we also require Claim 2For m ∈writeThen there existssuch that ProofLet a = (a1,a2) ∈A2. For 1 ≤i ≤2, takethatWriteThen we have This completes the proof of the claim. Claim 3Suppose that l ≥3.For mThen there existssuch that ProofLet n ∈Al?2and b ∈If n+DRb ∈Al?2, then n ∈. Thus The claim follows from (7.2) and Claim 2. Write Suppose that there exists d ∈A suth thatfor some b,∈B. Since we have from which it follows that d=0. Thus, we obtain By Theorem 1, we have Case 2Suppose that r =1.Without loss of generality,we assume thatsuch that Take S ∈N with S ≥4 and D ∈A×such that If l ≥2, we also require Claim 4For m ∈GS, writeThen there existssuch that ProofLet a ∈A. Takeandsuch thatWriteThen we have For m ∈GS, writeFor each a ∈Am, we fix asuch that=a. Since This completes the proof of the claim. Claim 5Suppose that l ≥2.For mwrite ProofThe claim follows from the similar argument as in Claim 3. Write By using similar arguments as in Case 1, we obtainthe theorem follows from (7.5). Combining the above two cases, the proof of the theorem is completed.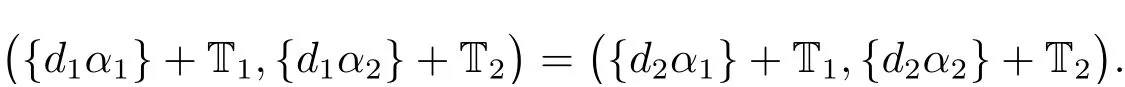

3 Estimate for G
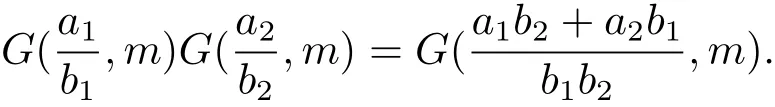
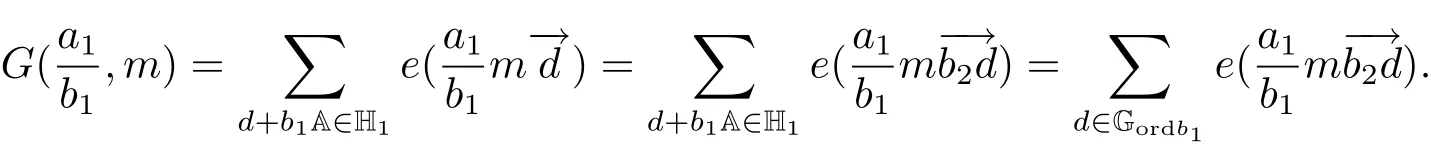
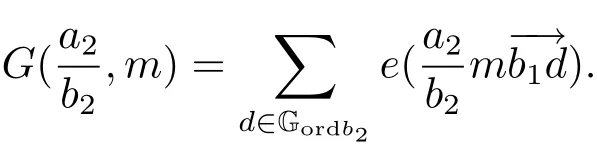
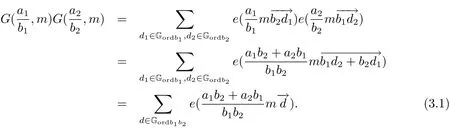
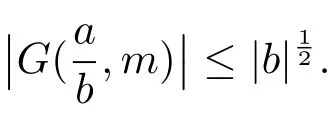
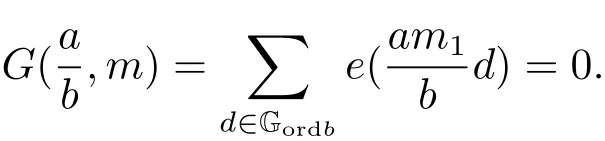
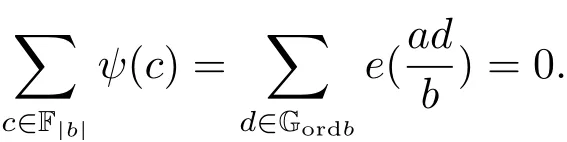
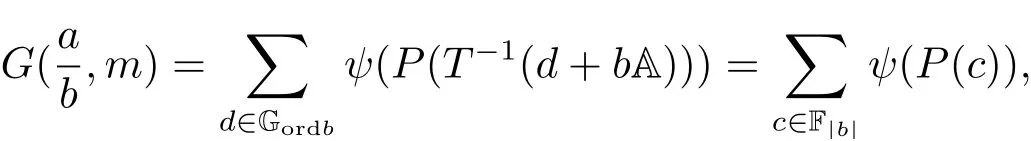

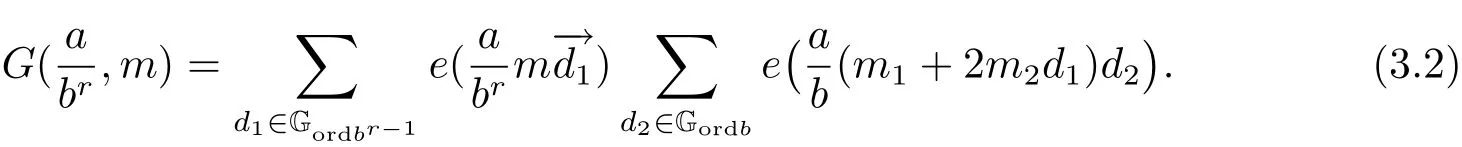
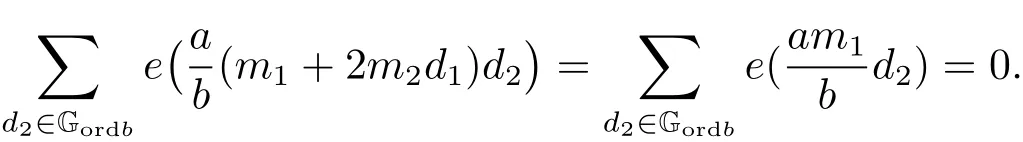
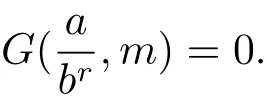
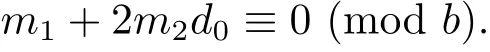
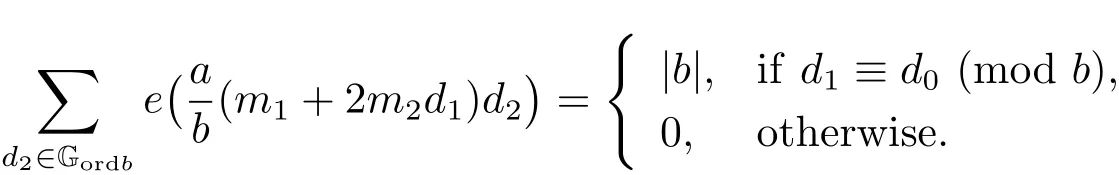
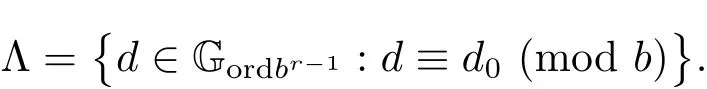




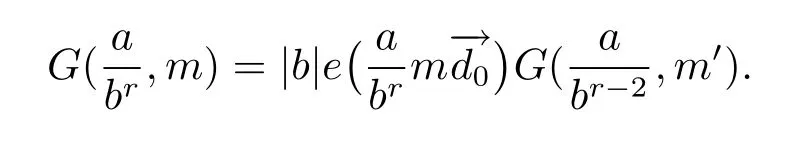
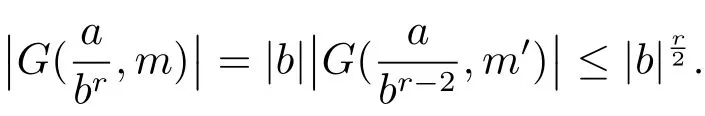
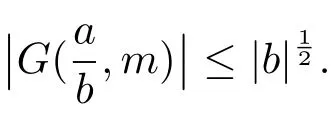
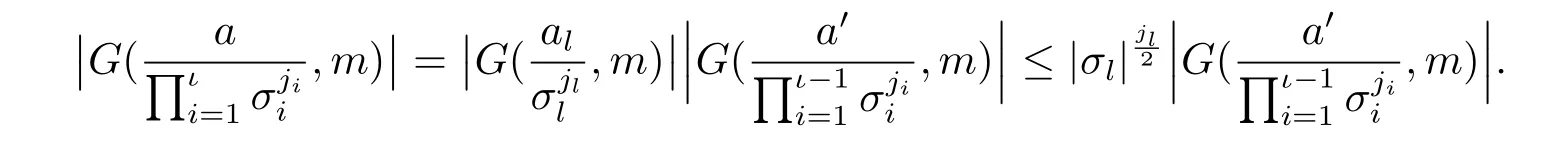
4 Estimates for SN
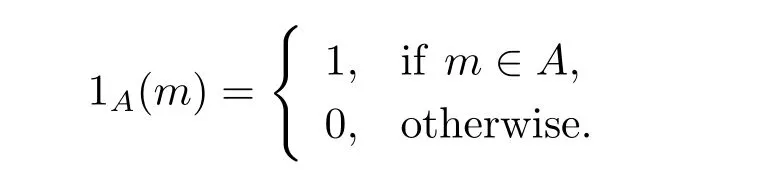
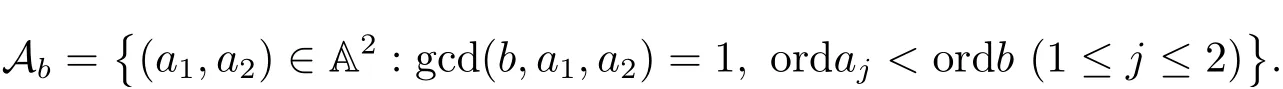
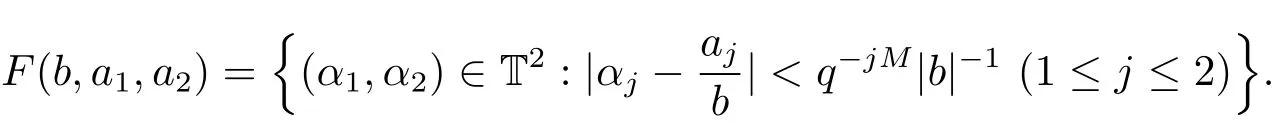
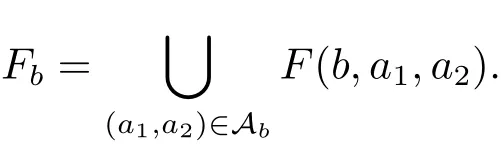
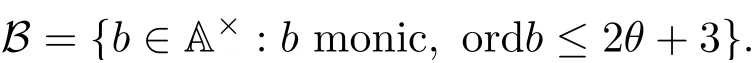
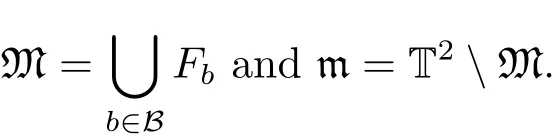
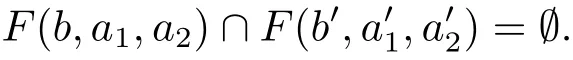
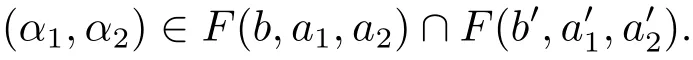
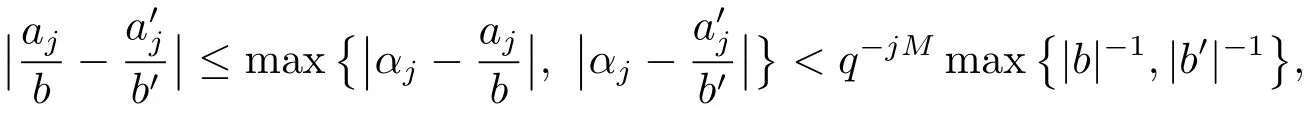
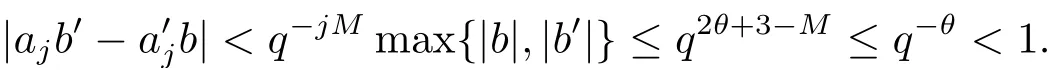
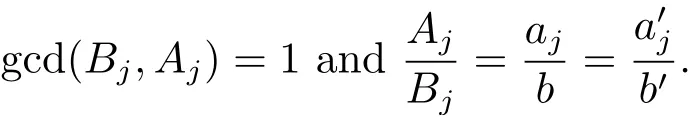


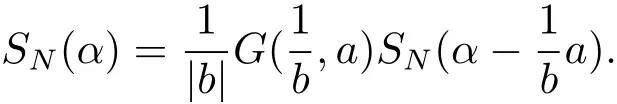
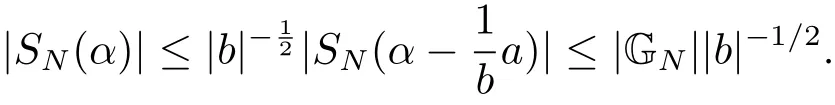

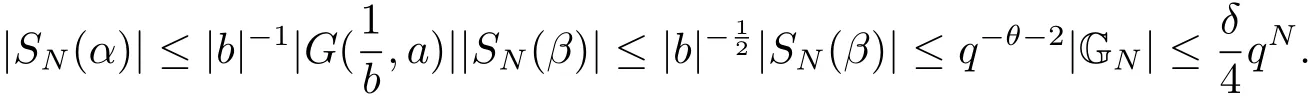
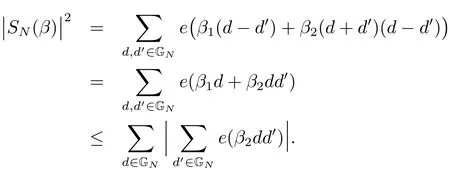
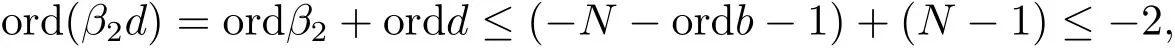

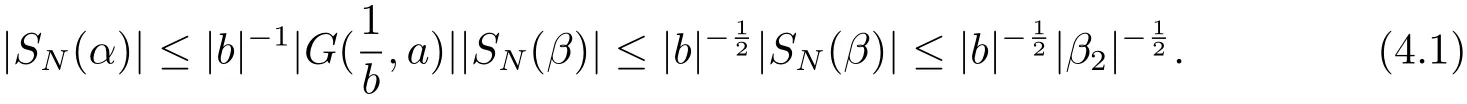

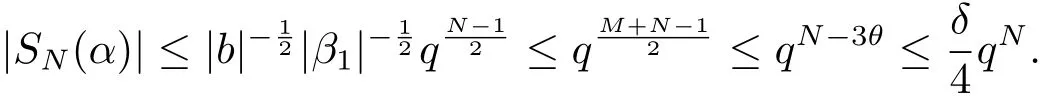


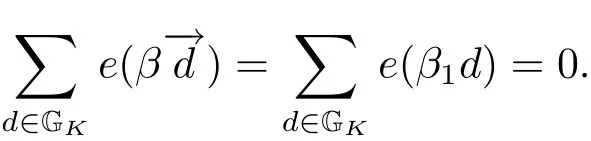

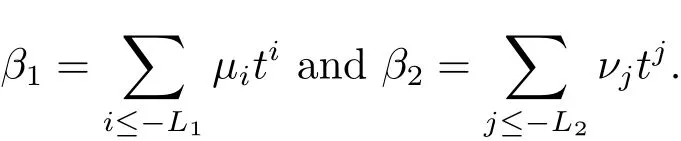
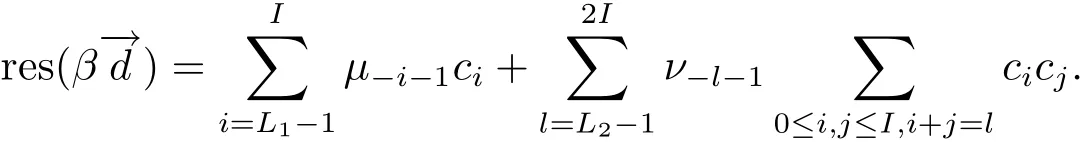
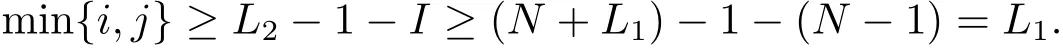

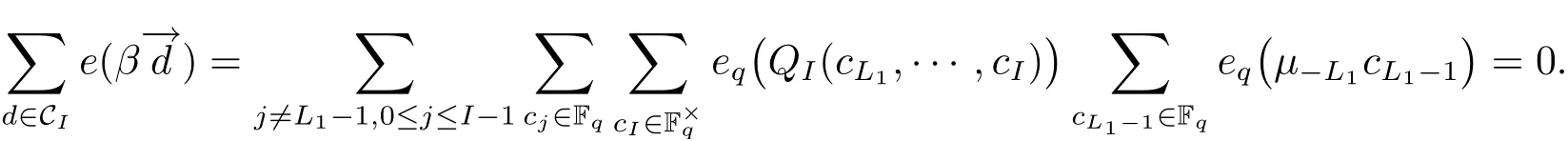
5 Density Increment
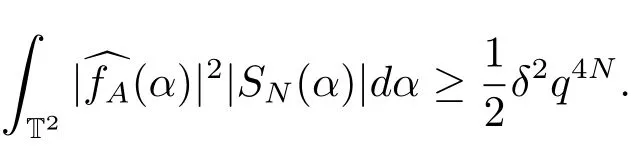
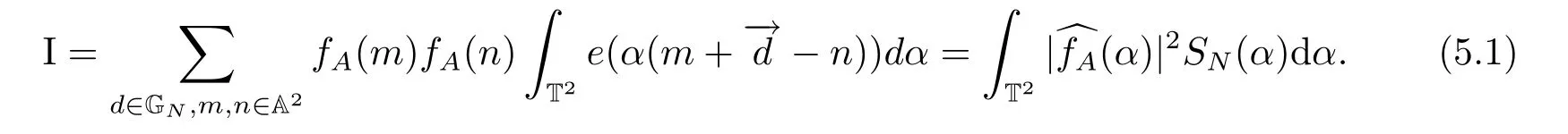
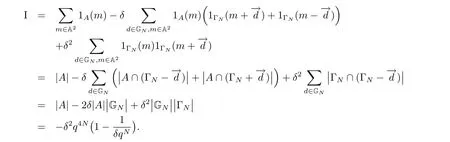


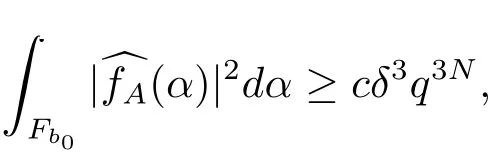
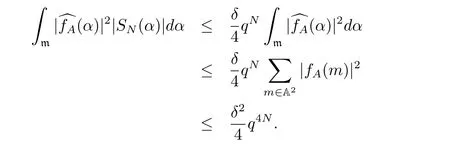
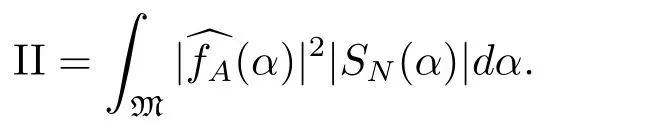



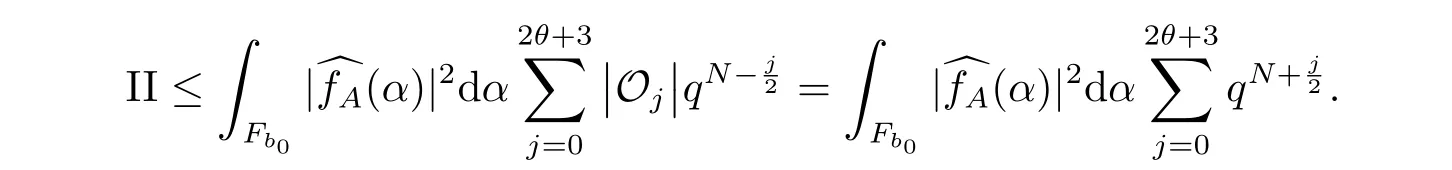

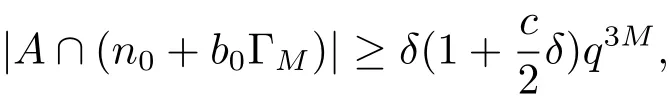



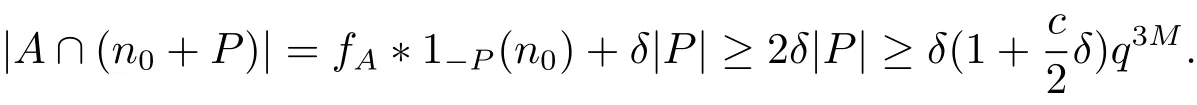

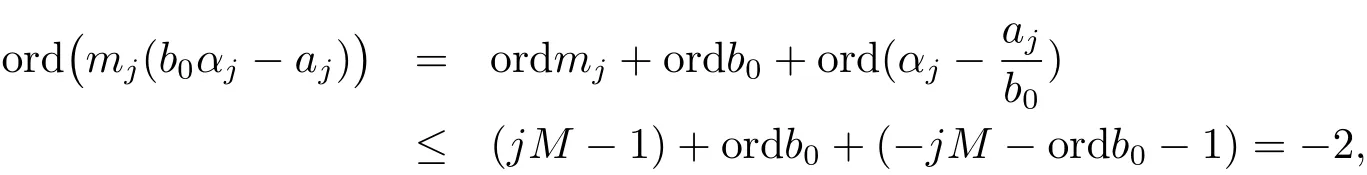
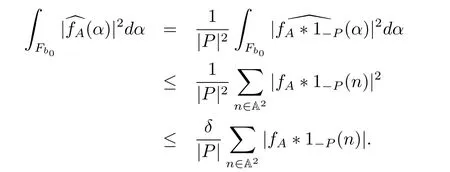
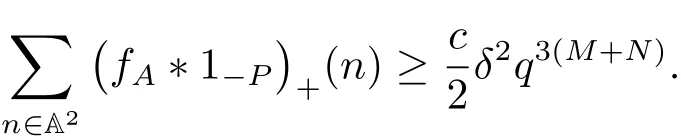
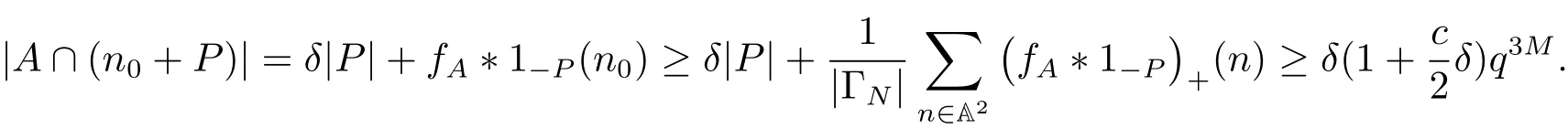
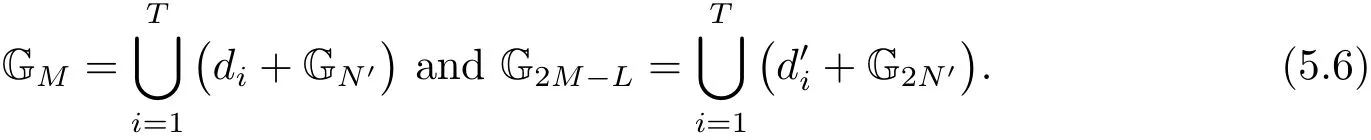
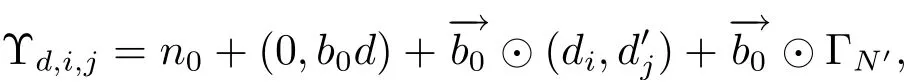

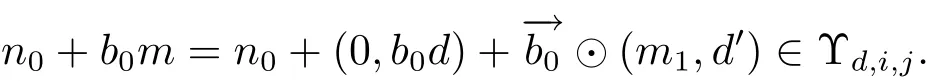
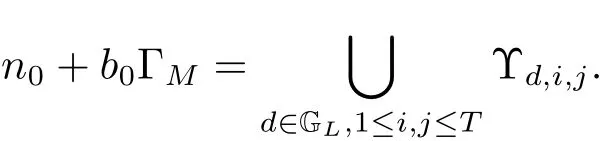
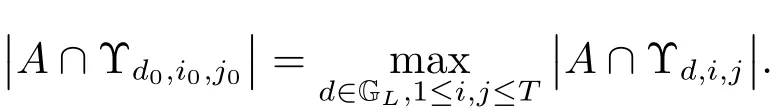
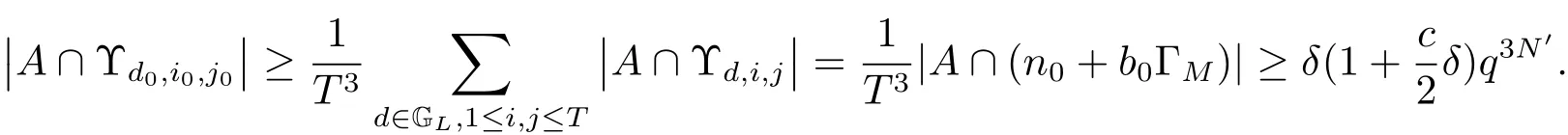
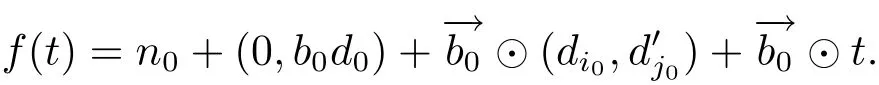

6 Proof of Theorem 1
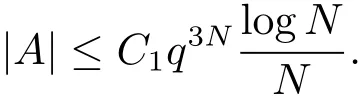
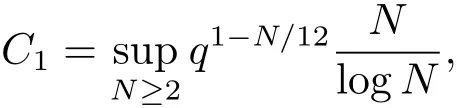


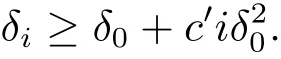
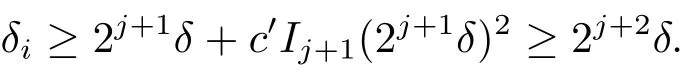
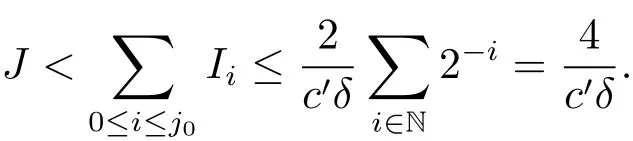
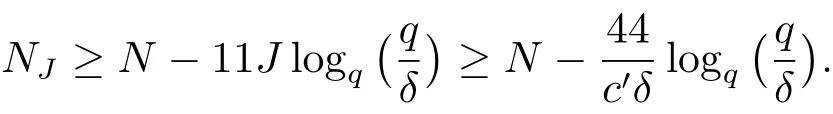
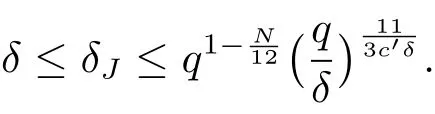
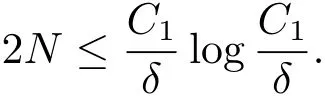

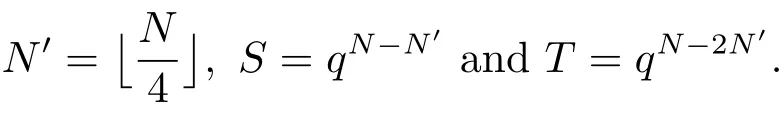
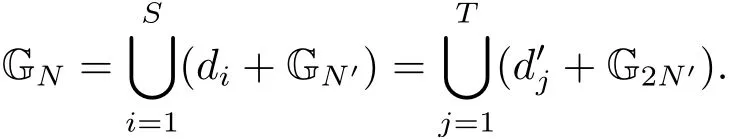
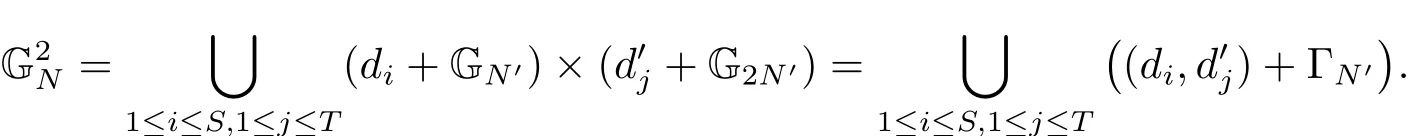
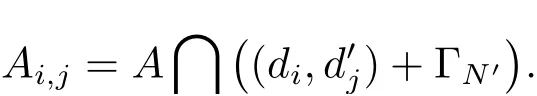
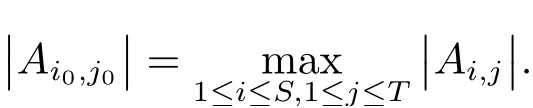
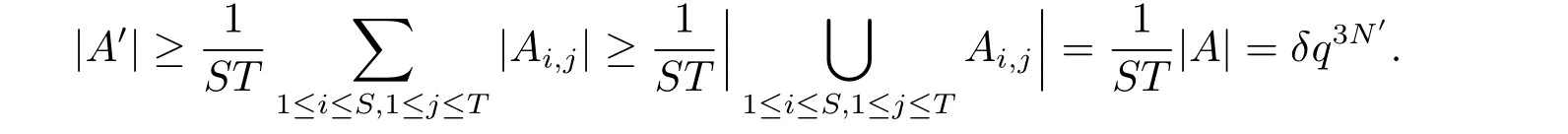
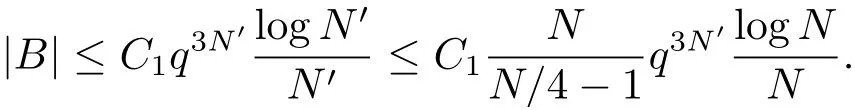
7 Proof of Theorem 2