Constraints on H0 from WMAP and BAO Measurements?
Xue Zhang (張雪) and Qing-Guo Huang (黃慶國),3,4
1Center for Gravitation and Cosmology,College of Physical Science and Technology,Yangzhou University,Yangzhou 225009,China
3School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
Abstract We report the constraints of H0obtained from Wilkinson Microwave Anisotropy Probe (WMAP) 9-year data combined with the latest baryonic acoustic oscillations(BAO)measurements.We use the BAO measurements from 6dF Galaxy Survey (6dFGS),the SDSS DR7 main galaxies sample (MGS),the BOSS DR12 galaxies,and the eBOSS DR14 quasars.Adding the recent BAO measurements to the cosmic microwave background (CMB) data from WMAP,we constrain cosmological parameters ?m=0.298±0.005,H0=68.36+0.53?0.52 km·s?1 ·Mpc?1,σ8=0.8170+0.0159?0.0175in a spatially flat Λ cold dark matter (ΛCDM) model,and ?m=0.302±0.008,H0=67.63±1.30 km ·s?1 ·Mpc?1,σ8=0.7988+0.0345?0.0338in a spatially flat wCDM model,respectively.Our measured H0results prefer a value lower than 70 km·s?1·Mpc?1,consistent with the recent data on CMB constraints from Planck (2018),but in 3.1 and 3.5σ tension with local measurements of SH0ES(2018)in ΛCDM and wCDM framework,respectively.Our results indicate that there is a systematic tension on the Hubble constant between SH0ES and the combination of CMB and BAO datasets.
Key words: Hubble constant,cosmic microwave background,baryon acoustic oscillation
1 Introduction
The Hubble constantH0are in tension between the CMB measurements from Planck[1?2]and the type Ia supernova measurements from SH0ES (SNe,H0,for the Equation of State of dark energy).[3?4]The value ofH0can be determined by the local measurements from Hubble Space Telescope (HST) in a model-independent way,and the model-dependent global fitting from CMB data(see Ref.[5]for review on determining the Hubble constant).Riesset al.(2016)[3]reported a local determination ofH0=73.24±1.74 km·s?1·Mpc?1(2.4% precision) from Cepheids in the hosts of Type Ia supernovae(SNIa).Recently Riesset al.(2018)[4]improved the precision to 2.3%,yielding 73.48±1.66 km·s?1·Mpc?1.However,the Planck survey reportedH0=67.27±0.66 km·s?1·Mpc?1(0.98% precision; TT,TE,EE+lowP) in 2015[1]and 67.27±0.60 km·s?1·Mpc?1(0.89% precision; TT,TE,EE+lowE) in 2018[2]in the ΛCDM model.There exist a 3.7σtension between the latest results of Planck in the ΛCDM model and SH0ES.Addisonet al.(2016)[6]have discussed the internal tension inferred from the Planck data itself.They have analyzed the Planck TT power spectra in detail and found that the Hubble constantH0=69.7±1.7 km·s?1·Mpc?1at the lower multipoles(?<1000)andH0=64.1±1.7 km·s?1·Mpc?1at the higher multipoles (? ≥1000).
At present it is difficult to explain theH0disagreement in the standard cosmological model.See Refs.[7–26]for more literature onH0.The tensions among datasets could be due to some underestimated systematic error associated with the experiments.On the other hand,we cannot exclude the possibility of new physics beyond the ΛCDM cosmology,[27?33]so the extended models are expected.In order to be independent of Planck and SH0ES measurements,we also call for another independent precise CMB power spectrum measurement,namely WMAP.The 9-year WMAP(TT,TE,EE+BB)reported a 3%precision determination ofH0=70.0±2.2 km·s?1·Mpc?1in a spatially flat ΛCDM model.[34]And in Ref.[1]the authors reportedH0=68.0±0.7 km·s?1·Mpc?1in ΛCDM model for WMAP+BAO datasets,where the BAO included 6dFGS,SDSS DR7 MGS,BOSS DR11 LOWZ and CMASS.Since more BAO datasets were released after Ref.[1]and the analysis in Ref.[1]depends on the ΛCDM model,we extend the discussion in Ref.[1]in two aspects: one is that we use the latest BAO measurements from the 6dFGS survey,[35]the SDSS DR7 MGS,[36]the BOSS DR12 (9-zbin),[37]and the eBOSS DR14 measurement;[38]another is that we consider two cosmological models,namely ΛCDM andwCDM models.
Beyond the standard cosmological model and without SH0ES and Planck measurements,it would be necessary to study the Hubble constant constraints using the latest data.In this work we consider the WMAP data of CMB power spectrum,and combine with the latest BAO measurements (6dFGS+MGS+DR12+DR14).We analyze the data sets in detail to place constraints onH0in ΛCDM andwCDM model.This paper is organized as follows.In Sec.2,we will introduce the model and data sets used in this work.In Sec.3,we present our main results.Conclusions of our work are given in Sec.4.
2 Model and Data
In this paper we discuss the spatially flat ΛCDM andwCDM model.We firstly use the 9-year WMAP data(TT,TE,EE+BB) only,[34]and then combine it with the additional BAO data sets(including the 6dFGS survey,[35]the SDSS DR7 MGS,[36]the BOSS DR12,[37]and the eBOSS DR14 measurement.[38]Their effective redshifts and constraints are listed in Table 1.

Table 1 BAO distance measurements used in this work.
The angular diameter distance takes the form of
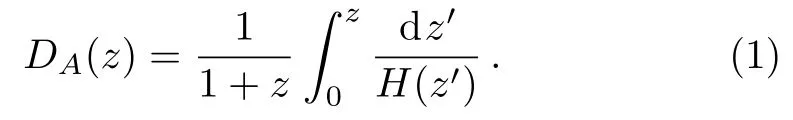
For the comoving sound horizon at the end of the baryon drag epochzd,we takerd≡rs(zd).DVis a combination of the angular diameter distanceDA(z) and Hubble parameterH(z),
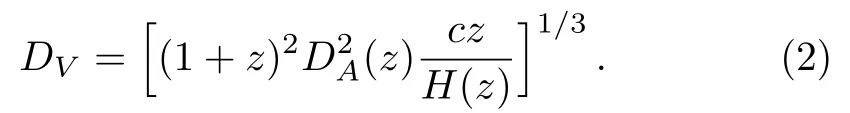
Our analysis employs the same Markov Chain Monte Carlo (MCMC) formalism used in previous analyses.[39?44]We use the CosmoMC package[45]to sample the parameter space.We explore the WMAP-only and WMAP+BAO likelihood with MCMC simulations of the posterior distribution for the six base parameters as given in Planck Collaboration.[1?2]The six basic parameters are the baryon density today,?bh2,the cold dark matter density today,?ch2,100×approximation tor?/DA,100θMC,the reionization optical depth,τ,the log power of the primordial curvature perturbations,ln(1010As),and the scalar spectrum power-law index,ns.This approach naturally generates the likelihoods of parameters,which are marginalized over all other fitting parameters.
3 Result
Figures 1 and 2 show 2-dimensional marginalized constraints on the basic MCMC sampling parameters in the ΛCDM model andwCDM model.We explore the posterior of parameters and plot against the following derived parameters(the Hubble constantH0,matter density parameter ?m,and late-time clustering amplitudeσ8).Here we plot the results using 9-year WMAP and combine BAO data sets (6dF+MGS+DR12+DR14,labeled by BAO).The blue contours show the constraints using 9-year WMAP data alone,and the red contours include WMAP+BAO datasets.It is easy to see that addition of BAO changes the constraints onH0,?m,andσ8,namely,it can effectively improve the WMAP-only constraints.
Figure 3 presents 68% and 95% likelihood contours of the ?m-H0plane for the WMAP+BAO data sets.The red contours correspond to a flat ΛCDM model and the blue contours correspond to thewCDM model.Figure 4 shows the marginalized likelihood distribution ofH0and summarized theH0measurements from Planck (2018) and SH0ES (2018).Blue line and red line show constraints in ΛCDM andwCDM model corresponding to 9-year WMAP and WMAP+BAO datasets respectively.Clearly,adding the latest BAO as a complementary to WMAP,our measuredH0results are consistent with the recent data on CMB constraints from Planck (2018),which prefer a value lower than 70 km·s?1·Mpc?1.

Fig.1 (Color online) Likelihood contours (68% and 95%) of cosmological parameters in a flat ΛCDM model derived from WMAP and WMAP + BAO respectively.

Fig.2 (Color online) Likelihood contours (68% and 95%) of cosmological parameters in a flat wCDM model derived from WMAP and WMAP + BAO respectively.
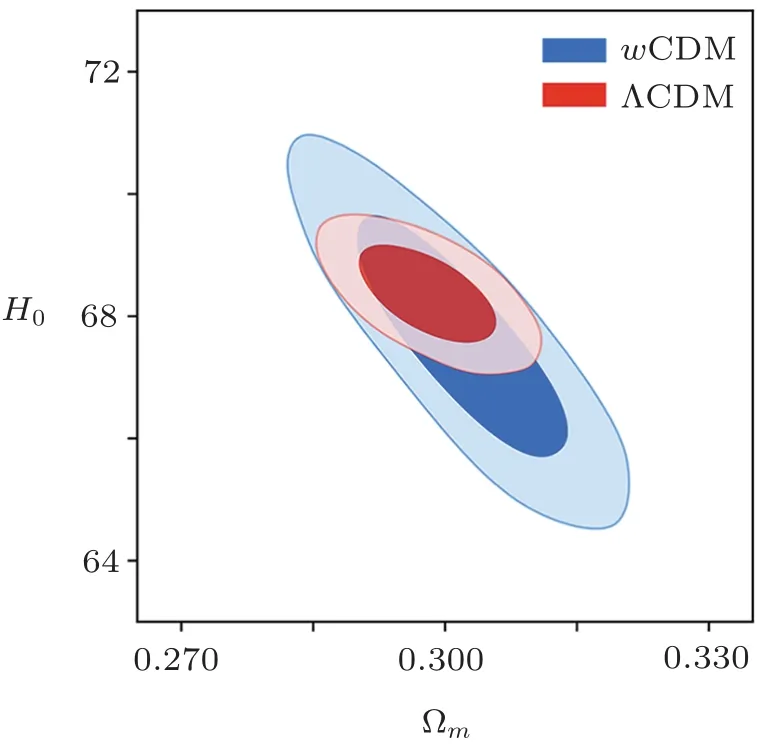
Fig.3 (Color online) Confidence contours for ?m-H0 in ΛCDM and wCDM model using WMAP+BAO datasets.
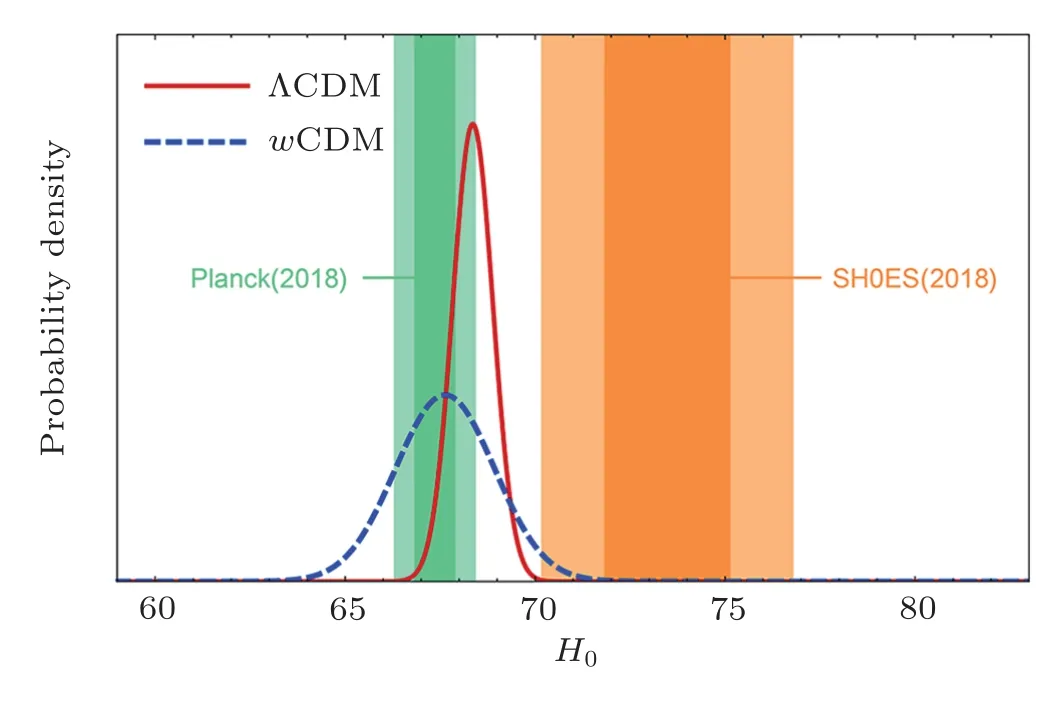
Fig.4 (Color online) Marginalized H0 constraints in the ΛCDM and wCDM model and comparison of the SH0ES and Planck measurements.

Table 2 Parameter constraints in ΛCDM and wCDM from the WMAP with and without BAO.
Table 2 gives the 68% confidence level of cosmological parameters in the ΛCDM model andwCDM model using WMAP and WMAP+BAO datasets.The first group is the base six parameters in ΛCDM model,which are sampled in the MCMC analysis.InwCDM modelwis an additional sampling parameters.The second group lists the constraints of three representative derived parameters (H0,?m,andσ8).The third group shows theχ2of WMAP and each BAO datasets.The column labeled“WMAP” is 9-year WMAP only.The first two columns give results of six parameter ΛCDM from 9-year WMAP data without and within BAO measurements.The last two columns give the results inwCDM framework from WMAP data only and when BAO are added.Adding BAO measurements to WMAP,we constrain cosmological parameters ?m=0.298±0.005,H0=km·s?1·Mpc?1(0.78% precision),σ8=in a spatially flat ΛCDM model,and ?m=0.302±0.008,H0=67.63±1.30 km·s?1·Mpc?1(1.93% precision),σ8=in a spatially flat wCDM model.The combined constraint onwfrom WMAP+BAO in a spatially flatwCDM model isw=?0.96±0.07.Compared with the WMAP alone analysis,the WMPA+BAO analysis reduced the error bar ofH0by 75.4% and 95.3% in ΛCDM model andwCDM model,respectively.However,they are still in 3.1 and 3.5σtension with local measurements of Riesset al.(2018) in ΛCDM andwCDM framework,respectively.
4 Summary and Discussion
In this paper,we determine the Hubble constantH0using the CMB data from WMAP and the latest BAO measurements (6dFGS+MGS+DR12+DR14) in a spatially flat ΛCDM andwCDM cosmology.Adding BAO measurements to WMAP,we constrain cosmological parameters ?m=0.298±0.005,H0=68.36km·s?1·Mpc?1(0.78%precision),σ8=0.8170in a spatially flat ΛCDM model,and ?m=0.302±0.008,H0=67.63±1.30 km·s?1·Mpc?1(1.93%precision),σ8=0.7988in a spatially flatwCDM model.The combined constraint onwinwCDM model from WMAP+BAO datasets isw=?0.96±0.07.By adding the latest BAO as a complementary to WMAP,our measured results ofH0consistent with the constraint from Planck (2018),which prefers a value lower than 70 km·s?1·Mpc?1.However,there are 3.1 and 3.5σtension with local measurement of Riesset al.(2018) in ΛCDM andwCDM framework,respectively.Compared with the WMAP-only analysis,the WMPA+BAO analysis reduces the error bar ofH0by 75.4% in ΛCDM model and 95.3% inwCDM model.
Our results indicate that the combination of WMAP and BAO datasets gives a tight constraint on the Hubble constant comparable to that adopting Planck data.In order to soften the model-dependent constraint using CMB and BAO data,we also extend our analysis to more general dark energy model(wCDM cosmology),but there is still a significant tension between the global fitting CMB+BAO datasets and local determination.
Acknowledgements
We acknowledge the use of HPC Cluster of ITP-CAS.
 Communications in Theoretical Physics2019年7期
Communications in Theoretical Physics2019年7期
- Communications in Theoretical Physics的其它文章
- Tunable Range Interactions and Multi-Roton Excitations for Bosons in a Bose-Fermi Mixture with Optical Lattices?
- Holographic Entanglement Entropy: A Topical Review?
- Doubly Excited 1,3Fe States of Two-Electron Atoms under Weakly Coupled Plasma Environment?
- A Renormalized-Hamiltonian-Flow Approach to Eigenenergies and Eigenfunctions?
- Scalar Tensor Cosmology With Kinetic,Gauss-Bonnet and Nonminimal Derivative Couplings and Supersymmetric Loop Corrected Potential
- Hydrodynamic Stress Tensor in Inhomogeneous Colloidal Suspensions: an Irving-Kirkwood Extension?
