Sahameddin Mahmoudi Kurdistani*, Giuseppe R. Tomasicchio, Felice D'Alessandro,Leila Hassanabadi

Department of Engineering for Innovation, University of Salento, Lecce 73047, Italy

Abstract A new equation is proposed for the design of armor units on protected river banks under the combined action of ship-induced waves and river flow.Existing observed field and experimental data in the literature have been examined and a valuable database has been developed.Different conditions,including the river water depth,flow velocity,river bank slope,Froude number,wave height,wave period,and wave obliquity have been considered.Results from an empirical equation(Bhowmik,1978)that only considers the maximum wave height and river bank slope have been compared with the results calculated by the newly developed equation.Calculated results have also been verified against field data.Results show that not only the maximum wave height and river bank slope but also the water depth,flow velocity,wave length,wave obliquity,and wave period are important parameters for predicting the mean diameter of the armor units, highlighting the multivariate behavior of protecting the river bank in the presence of ship-induced waves and river flow velocity.

Keywords: River bank protection; Hydraulics; Ship-induced waves; River flow velocity; Wave period; Wave obliquity; Multivariate phenomenon

1. Introduction

Erosion control is an important topic in river and coastal engineering. High-velocity flows in rivers and high waves impinging on the coastline can cause erosion. An armor layer made of rocky units is an erosion control structure that can reduce or prevent the erosion process if well designed. Armor layers have been used extensively in erosion prevention works because they are made of natural materials that are easily available in many areas. Moreover, it is a flexible structure,and under attack by river currents, sea waves, and shipinduced waves, it can remain functional even if some stones are moved.

The successful design of armor units mainly depends on the selection of the stone size, identified as the mean diameter of the protecting armor units (D50). There have been several contributions in previous studies to estimation of D50for river bank armor unit design focusing on river flow velocity. This study intended to propose a new formula to predict the mean diameter of armor units protecting the river bank under the combined action of ship-induced waves, ship travel direction with respect to river flow direction, and river flow velocity.

The previous literature on ship-induced waves includes the contributions by Kelvin (1887), Havelock (1908), Lunde(1951), Birkhoff et al. (1954), and Johnson (1957). More recently,Gelencser(1977)showed that the damage caused by a passing ship in a restricted canal is a result of two principal agents: the ship-induced drawdown and waves. Herbich and Schiller (1984) focused on surges and waves generated by ships navigating a restricted channel; they found that the wave induced by a large ship is a function of its draft and speed,while the wave generated by a small ship is principally a function of the speed. Sorensen and Weggel (1984) developed a model to predict ship-induced wave height at a given location when a ship's speed and displacement, water depth,and distance from the sailing line are known. Hochstein and Adams(1989)considered the influence of ship movements on bank stability in restricted channels; they developed a numerical model incorporating the effects of ship-induced backwater velocity, propeller jet velocity, and surface waves. Nanson et al. (1994) investigated the erosion at an unprotected river bank caused by ship-induced waves in the Gordon River in Tasmania (Australia) and found that the maximum wave height indicates a major threshold in wave erosive potential at a height of about 30-35 cm in relatively non-cohesive sandy alluvium. As a result of these findings,speed restrictions were placed on all large ships cruising along the Gordon River in order to keep maximum wave heights at less than 30 cm. Huesig et al. (1999) experimentally studied the impacts of high-speed cargo ships on inland waterways and found that ship-induced reverse flow velocities under the ships are critical for the stability of beds.Schu¨ttrumpf (2006) studied the hydraulic influence of navigation channels on flood defense structures in the Elbe Estuary in Germany, and found that the amplitudes of shipinduced pore pressure variations or vibrations at the dike cannot be the reason for the observed dike failures at the Elbe Estuary. De Roo et al. (2012), by means of field measurements in the Lys River in Belgium, showed that ship-induced hydrodynamics directly influence the sediment transport dynamics in the bank protection. De Roo and Troch (2013)conducted field monitoring of ship-induced wave action on eco-friendly bank protection (timber piling in combination with vegetation) in a confined waterway. Macfarlane et al.(2014) developed a freely available wave wake predictor to estimate ship-induced wave wake characteristics. G¨oransson et al. (2014) investigated ship-induced waves and turbidity in the G¨ota ¨Alv River in Sweden, which was a part of the dataset used in this study. They found that because of the longer period for the drawdown, the maximum turbidity is mainly determined by drawdown, while for bank erosion,both the drawdown and the divergent waves are important. Ji et al. (2014) presented a three-dimensional (3D) numerical model based on hydro-sedimentary coupling to examine the relationship between the sediment movement and the pattern of ship-induced waves around and faraway from the ships.They showed that the rate of re-suspended sediment is four times greater when the propeller power is doubled. He et al.(2015)numerically compared three simple models of Kelvin's ship wake considering the simple theoretical framework of steady, deep-water, and linear potential-flow hydrodynamics,respectively. Bellafiore et al. (2018) conducted a series of field experiments on ship wake formation and propagation in the Venice Lagoon and its major waterway and found that smaller and faster ships have less of an impact on the tidal flats than larger vessels navigating at relatively lower speeds.

All the above-mentioned contributions focused on shipinduced wave hydraulics and related bank failure without commenting on the mean diameter of the armor units used to protect the bank. Bhowmik and Schicht (1980), using an empirical equation(Bhowmik,1978),determined the values of the mean diameter of stable armor units for different reaches of the Illinois River that were used as a part of the dataset in this study. Bhowmik et al. (1982) prepared a large dataset of measured waves generated by river traffic and wind, which was used in this study to verify the newly proposed equation.Van der Meer(1988)developed a practical design formula for the armor layer of rubble mound revetments and breakwaters under wind-induced wave attacks. There are few studies on armor unit design for river bank protection in the literature.Wang and Shen (1985) studied armor unit design based on incipient sediment motion theory,using the Shields parameter for both unidirectional flow and wave conditions; they found that, for wave motion, greater flow shear stress is required to cause incipient motion, due to the shorter contact time between maximum orbital velocity near the bottom and the sediment particle. Maynord and Abt (1989) developed an armor unit design procedure based on local average flow velocity and water depth for straight and curved channels.D'Angremond et al. (1992) carried out full-scale tests on the behavior of gabions installed prior to beach nourishment to limit erosion during severe storms. Shafai-Bajestan and Albertson (1993) studied armor unit criteria downstream of pipe outlets, developing a general relationship for incipient motion of sediment below a jet, considering the effects of armor unit gradation. Gisonni and Hager (2006) presented an armor unit design procedure for spur protection; physical model tests allowed for evaluation of the effects of various parameters on the spur performance and its armor unit failure,using a modified Shields approach. Pagliara and Kurdistani(2015) experimentally studied riverbed stabilization and bank protection using rock vanes in meandering rivers.

2. Methodology

A dimensional analysis was conducted by means of the Buckingham theorem and incomplete self-similarity, as described by Barenblatt (1987). The main parameters used to determine D50are

where f is a functional symbol; h is the water depth; u is the river flow mean velocity; ρsis the armor unit density; ρ is the water density; g is the gravitational acceleration; H is the maximum wave height, with H = 2.2Hs, where Hsis the significant wave height (Tomasicchio, 2011); T is the wave period;z is the river bank slope,and z=cot β,where β is the bank slope angle;θ is the wave attack angle with respect to the river bank, and θ′is the wave obliquity (Fig. 1 shows that when the ship moves upstream the wave angle is positive and equal to θ′, and when the ship moves downstream the wave angle is negative and is equal to -θ′); and C is the wave celerity.

As navigable rivers have a water depth greater than the length of ship-induced waves, the intermediate water wave condition (between shallow and deep water) was considered.Therefore,

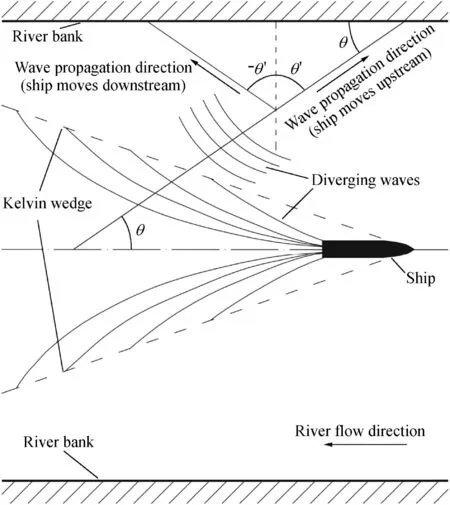
Fig.1.Kelvin wave pattern and wave propagation angle toward river bank.

where L is the wave length (USACE, 1984).

Based on incomplete self-similarity (Barenblatt, 1987),Eq. (1) can be written as

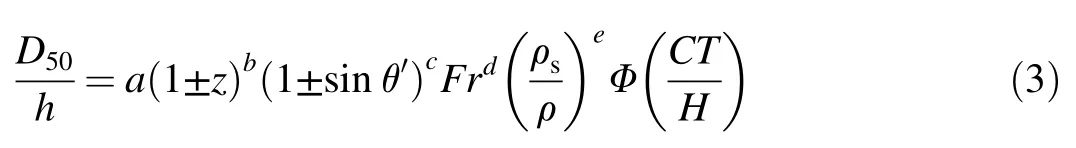
where a,b,c,d,and e are constant coefficients to be obtained experimentally;Fr is the Froude number of the river flow;and Φ is a functional symbol.Eq.(3)allows for the determination of D50for the units of the armor layer protecting the river bank under the combined action of ship-induced waves and river flow.

3. Model development

3.1. Dataset creation

G¨oransson et al. (2014) studied ship-induced waves at the Garn Station, along the G¨ota ¨Alv River in Sweden, where the cross-section has a mean bank slope of z≈8. They measured wave characteristics such as drawdown height, maximum wave height,and wave period induced by the passage of ships with different properties such as travel direction, speed, draft,length, and width for different river hydraulic conditions including river flow, mean flow velocity, and maximum water depth. According to Johnson (1957), Soulsby (1997), and G¨oransson et al. (2014), the bed shear stress, τb, can be defined as

where fwis the wave friction factor, and Udwis the maximum drawdown velocity, determined as follows:

where hdwis the drawdown height. Soulsby (1997) assumed fwto be

where A is the length scale and z0is the roughness length,with z0=ks/30,where ksis the roughness height with ks=0.2 mm(approximated by Soulsby (1997)). Finally, according to Soulsby (1997) and G¨oransson et al. (2014), A can be written as

To determine D50,the value of the Shields parameter τ*for the incipient motion was considered as follows:Since the target was protecting the river bank,the following expression is presented:

where τzis the bank shear stress, and k is a coefficient expressed by

where φ is the angle of repose of the rock material (Dey,2014). Therefore, substituting τzinstead of τbin Eq. (8), the value of D50for protecting the river bank can be determined as

Based on the observations from G¨oransson et al. (2014)and following the procedures described above, it was possible to determine the values of D50needed to protect the G¨ota ¨Alv river banks. The database was enriched from observations conducted by Bhowmik and Schicht (1980) at 23 reaches of the Illinois River in the presence of windgenerated waves propagating in the direction normal to the bank and along the direction of maximum fetch.Bhowmik and Schicht (1980) determined the value of D50for a stable protecting armor layer by means of Eq. (12)(Bhowmik, 1978), taking into account only the wave height and river bank slope and without considering the river flow conditions:

where W50is the mean weight of the unit of the armor layer in kilograms,Gs=ρs/ρ,and Hsis the significant wave height in meters.

3.2. Proposed formula

Empirical formulas such as Eq. (12) that include only the effect of the wave height and river bank slope were determined based on wind waves, and generally wind waves are much higher than ship-induced waves. Therefore, it is essential to find a model that is able to show the effect of the combination of the river flow,wave characteristics,and ship travel direction with respect to the river flow direction on the values of D50needed to protect the river banks in the presence of shipinduced waves. Using Eq. (2), a non-dimensional wave parameter λ was defined as follows:

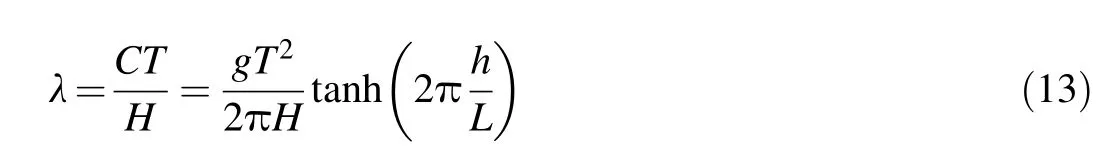
Eq. (3) can be rewritten as

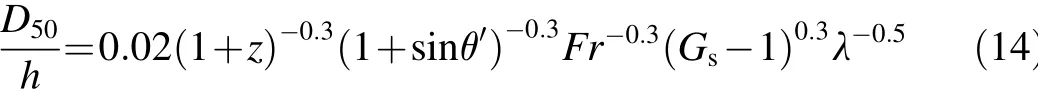
All adopted calibration data are shown in Fig. 2. “U” and“D” refer to the ship travel directions (upstream and downstream, respectively),which are presented along with the ship names in Fig. 2. It appears that Eq. (14) fits well with all adopted data, within the range of 30% deviation from the perfect agreement line. According to Barenblatt (1987), if for any reason complete similarity cannot be achieved, as in the case that one or more dimensionless parameters in the model and prototype cannot be kept at the same value, “incomplete similarity” would be the solution. Self-similar solutions generally lead to a power-law relationship with a selfsimilarity character (Barenblatt, 1987). In the current study λ was considered the self-similarity character that contains the water depth and all-important wave parameters such as wave height, wave length, and wave period. Based on incomplete self-similarity, independent of the other variables, D50could be a function of λ.Considering the non-dimensional parameter ξ =[Fr（1+sinθ′）（z+1）/（Gs-1）]-0.3,and defining normalized armor unit diameter D*= （D50/h）/ξ, Eq. (14) can be rewritten as

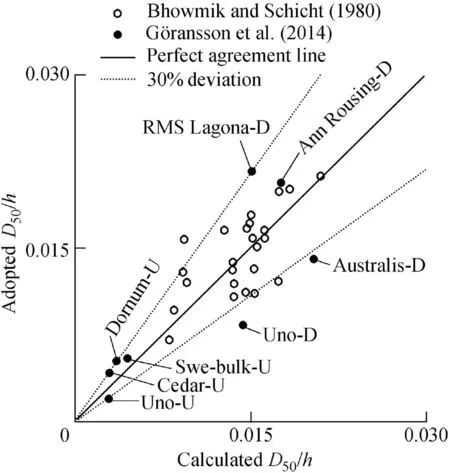
Fig.2.Comparison of calculated(using Eq.(14))and adopted values of D50/h.

Fig. 3 depicts the relationship between D* and λ, in which D*decreases with the increase of λ.

The relationship between D50/h and λ is shown in Fig. 4.Some data are labeled in Fig.4 to show the influence of different parameters such as the Froude number,river bank slope,and the travel direction of ships.For example,for the G¨ota River shipinduced data under the same river hydraulic conditions (Fr =0.11), for the ship “Uno” traveling downstream, Eq. (14) determines a greater value of D50/h than in the case of the same ship traveling upstream. Two points from the Illinois River windgenerated dataset illustrate the effect of the river bank slope;asexpected,a milderriverbanksloperesultsin asmallervalue of D50/h than the case of a steeper river bank in the same river flow conditions(Fr =0.11).Fig.4 shows also that,with decreasing λ,D50/h increases,and if λ increases,D50/h decreases.

4. Application of proposed formula

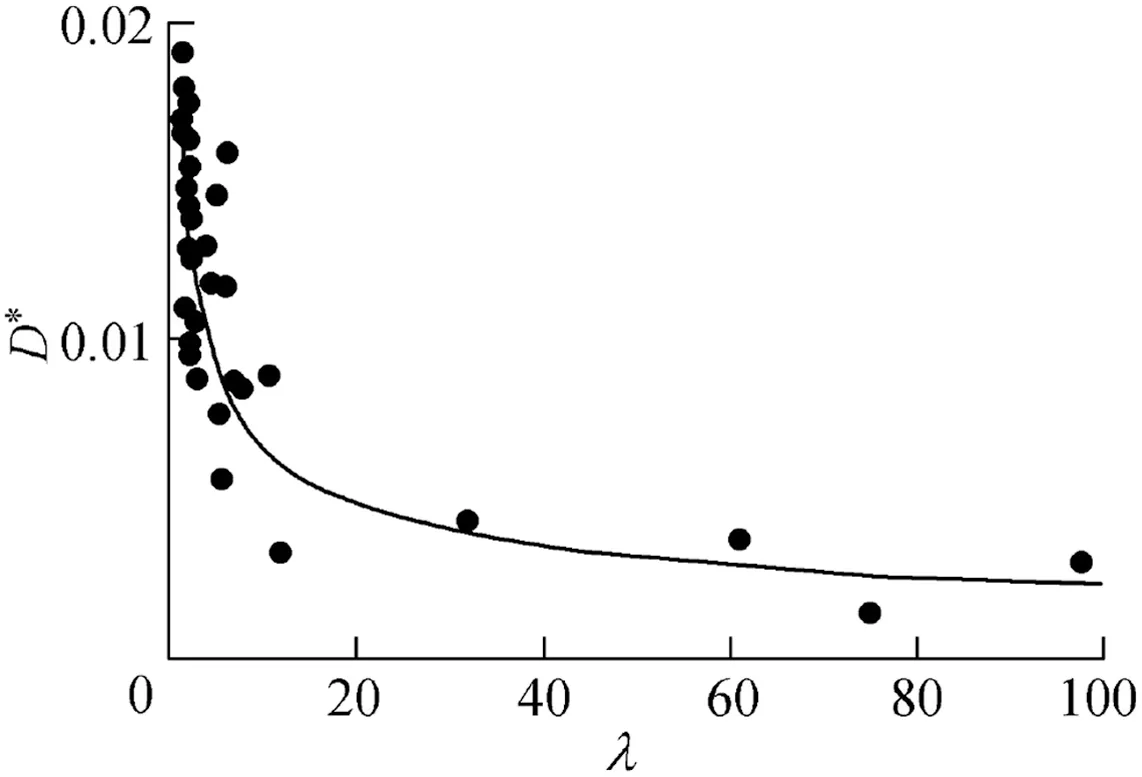
Fig. 3. Relationship between D*and λ.

Fig. 4. Relationship between D50/h and λ.

Bhowmik et al. (1982) measured the properties of waves generated by river traffic and compared them with the characteristics of waves generated by winds with return periods of two and 50 years.Since the main focus of the current study was river bank protection in the presence of shipinduced waves and there was no objective regarding extreme likelihood predictions,the 50-year data were not used and only waves generated by wind with a return period of two years were considered. Based on the data published by Bhowmik et al. (1982) and using the SPM method in the Shore Protection Manual, Volume 1 (USACE, 1984), the wave periods and consequently the wave lengths for the fetch limited conditions were determined.The river bank protection for the two cross-sections, Hadley's Landing and McEver's Island on the Illinois River,as well as the other two cross-sections,Rip Rap Landing and Mosier Island, on the Mississippi River, were examined, and the river flow and wind-induced wave characteristics are presented in Table 1, where zLand zRare the left bank and right bank slopes, respectively.

The results of Eq. (14) were compared with the results of Eq. (12), as shown in Fig. 5. Comparison of wave and flow characteristics for the left bank of the Rip Rap Landing cross-section (zL= 2.35) and Mosier Island crosssection (zL= 2.50) of the Mississippi River in Table 1 shows that all the parameters have almost the same values for both mentioned cross-sections except the river water depth:the water depth at the Rip Rap Landing cross-section is almost half the water depth at the Mosier Island cross-section.Because of this, the calculated values of D50using Eq. (14)for the left bank of the Rip Rap Landing cross-section are smaller than the determined values of D50at the Mosier Island cross-section, while Eq. (12) also results in smaller values for the Mosier Island cross-section, because it does not take into account the influence of the greater river water depth at the Mosier Island cross-section. Eq.(12)is highly sensitive to the wave height and there is no influence from the other wave and flow parameters.Independent of the flow characteristics in the river and other wave variables, increasing the wave height leads to an increase of W50in Eq. (12), and consequently an increase in the corresponding D50.

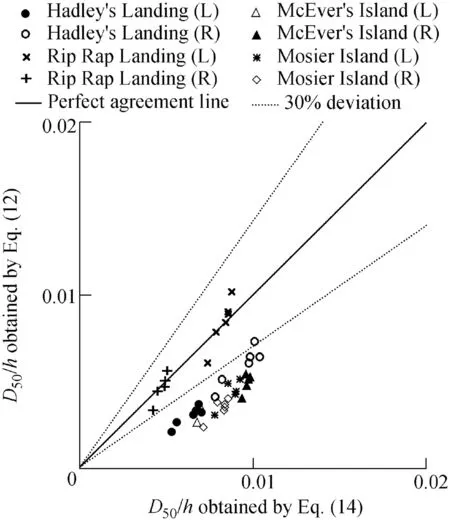
Fig. 5. Comparison of values of D50/h obtained by Eq. (12) and Eq. (14) for wind-generated waves based on wind records from Springfield,Illinois,for both left bank(L)and right bank(R)for twoyear return period and 6-h duration.

5. Discussion

Review of the data from G¨oransson et al. (2014) shows the difference between using Eq. (12) and using Eq. (14). Table 2demonstrates that, for ship passages in the G¨ota ¨Alv River,without consideration of the river flow characteristics such as river water depth and velocity, using Eq. (12), which contains only the effects of the ship-induced wave height and the river bank slope, leads to smaller values of D50in comparison with Eq. (14). This shows exactly the purpose of the current study.Generally,wind wave heights are higher than ship-induced wave heights, and for this reason, for wind-generated waves only,Eq. (12) gives results close to the results from Eq. (14). As a consequence,Eq.(12)for ship-induced waves only leads to lower values of D50than Eq. (14), which contains the effects of the river flow,cross-section geometry,and wave characteristics.

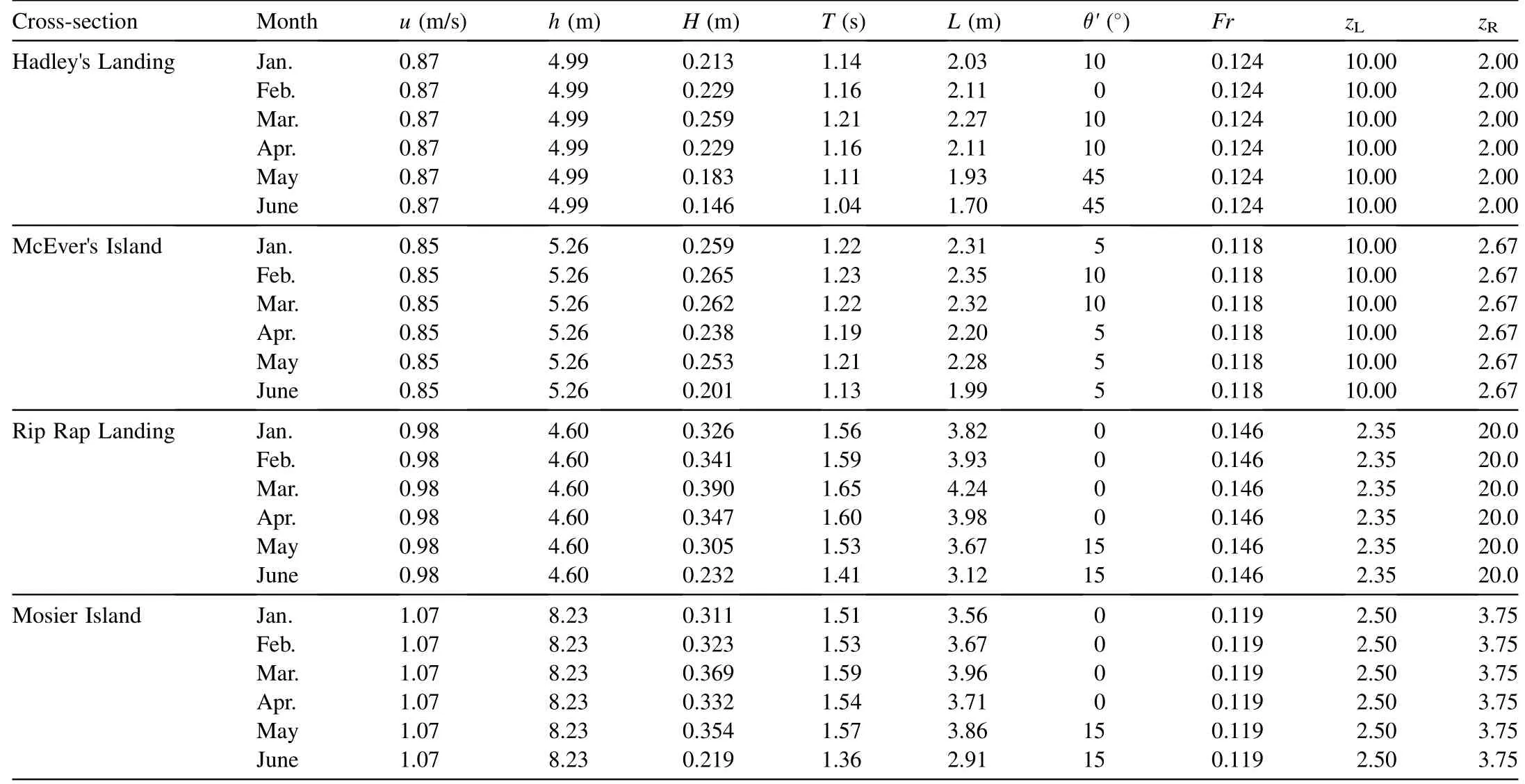
Table 1Wind-generated waves based on wind records from Springfield, Illinois, for two-year return period and 6-h duration.

In order to further examine this finding,the applications of Eq.(12)and Eq.(14)were examined using observed data from Bhowmik et al. (1982), which contains a series of measurements of ship-induced wave data collection in the Illinois and Mississippi rivers at the same cross-sections mentioned above.As it appears in Fig. 6, using Eq. (12) leads to an underestimation of D50for most of the adopted data in comparison to Eq. (14), because Eq. (12) does not consider the effect of the river flow and all wave characteristics. Fig. 7 shows that all data follow a unique trend in which increasing λ decreases D*as determined by Eq. (15).

Table 2Comparison of results of Eq. (12) and Eq. (14).

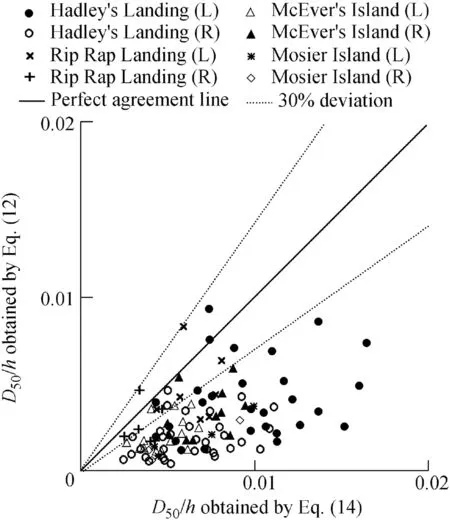
Fig. 6. Comparison of values of D50/h obtained by Eq. (12) and Eq. (14) for ship-induced wave data for both left bank (L) and right bank (R) of cross-sections.

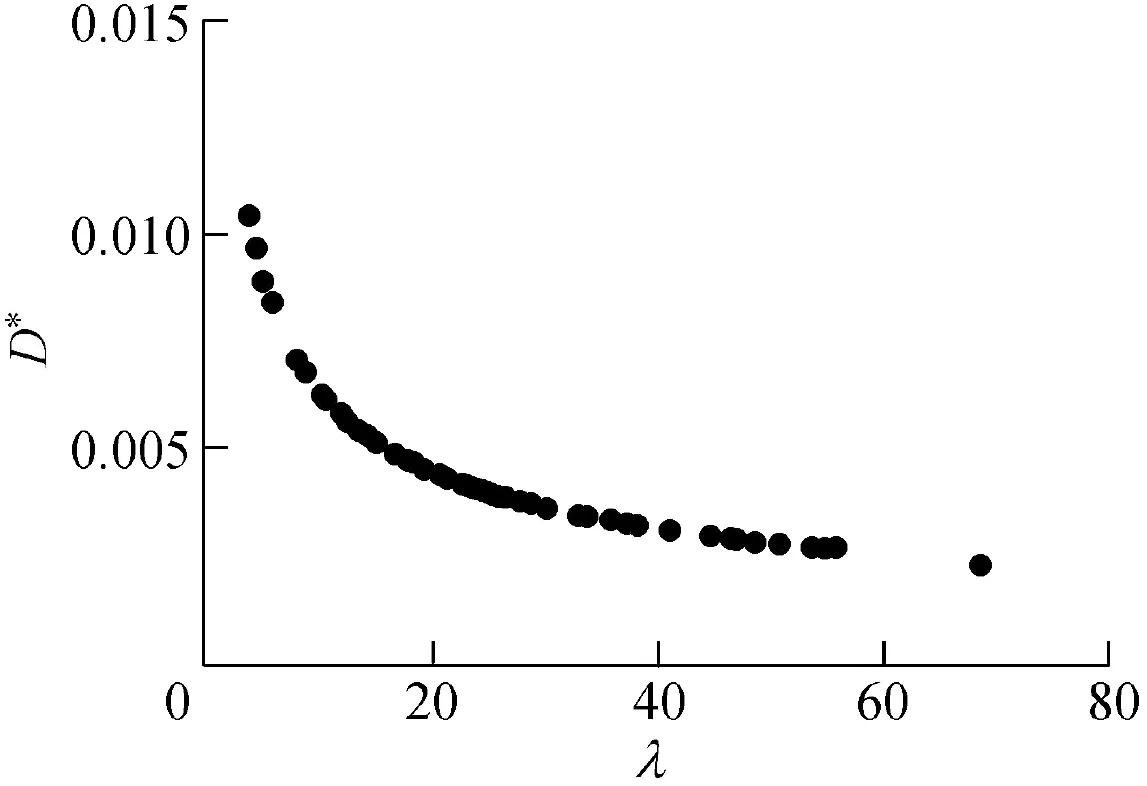
Fig.7.Decreasing values of D*by increasing λ for ship-induced wave data.

6. Conclusions

(1) Incomplete self-similarity and dimensional analysis resulted in a new equation predicting the mean diameter of the armor layer units for different combinations of river hydraulic conditions, river bank slopes, wave characteristics, and ship travel direction in the presence of ship-induced waves.

(2) A new dimensionless parameter, λ, showed that, not only the maximum height of the wave and river bank slope,but also the river water depth,wave length,wave period,wave obliquity, and ship travel direction are important parameters for predicting the mean diameter of the armor layer unit in the presence of ship-induced waves.

(3) Observations showed that increasing λ decreases the value of the mean diameter of the armor unit. The proposed formula was compared with both wind-generated wave data and ship-induced wave data adopted by Bhowmik et al.(1982). It is shown that the proposed equation can satisfactorily predict the mean diameter of the armor layer unit over a large range of both river hydraulic conditions and wind or ship-induced waves.

(4) Observed ship-induced wave data in unique river hydraulic conditions illustrated that, for a ship traveling downstream,a greater value of D50for the armor layer is needed to protect the river bank than for a ship traveling upstream.

(5) Results confirmed that previous empirical equations,such as Bhowmik's formula (Bhowmik, 1978), which include only wave height and bank slope, give results for windgenerated waves close to the results of the proposed formula in this study. However, for ship-induced waves, which have much lower heights than wind-generated waves, using Bhowmik's formula leads to lower values of D50with respect to the formulas that contain all the river flow and wave characteristics.

Acknowledgements

Fruitful discussion with Prof. Magnus Larson from Lund University is gratefully acknowledged.