Zeyu Xiong, Qiangqiang Shen, Yueshan Xiong, Yijie Wang and Weizi Li

Abstract: Word vector representation is widely used in natural language processing tasks.Most word vectors are generated based on probability model, its bag-of-words features have two major weaknesses: they lose the ordering of the words and they also ignore semantics of the words.Recently, neural-network language models CBOW and Skip-Gram are developed as continuous-space language models for words representation in high dimensional real-valued vectors.These vector representations have recently demonstrated promising results in various NLP tasks because of their superiority in capturing syntactic and contextual regularities in language.In this paper, we propose a new strategy based on optimization in contiguous subset of documents and regression method in combination of vectors, two of new models CBOW-OR and SkipGram-OR for word vector learning are established.Experimental results show that for some words-pair, the cosine distance obtained by the CBOW-OR (or SkipGram-OR) model is generally larger and is more reasonable than CBOW (or Skip-Gram), the vector space for Skip-Gram and SkipGram-OR keep the same structure property in Euclidean distance, and the model SkipGram-OR keeps higher performance for retrieval the relative words-pair as a whole.Both CBOW-OR and SkipGram-OR model are inherent parallel models and can be expected to apply in large-scale information processing.

Keywords: Distributed word vector, continuous-space language model, hierarchical softmax.

1 Introduction

A word vector representation is a mathematical processing object associated with each word.Generating word representations is an essential task of natural language processing (NLP) [Bengio, Ducharme and Vincent (2001);Collobert and Weston (2008)].Many NLP tasks such as sentiment analysis,sentence or text classification and so on consider words as basic units.An important step is the introduction of continuous representations of words [Bengio, Ducharme, Vincent et al.(2003)].When it comes to texts, one of the most commonly used fixed-length features is bag-of-words.Traditionally,the default word representation regards a word as a one-hot vector,which shares the same size of the vocabulary.Despite its popularity,bag-of-words features have two major weaknesses: They lose the ordering of the words and they also ignore semantics of the words.In order to address these issues,Cao et al.use the histogram of the bag of words model(BOW)to determine the number of sub-images in the image that convey secret information for the purpose of improving the retrieval efficiency[Cao,Zhou,Sun et al.(2018)].

Continuous-space language models[Holger(2007);Bengio,Schwenk,Senécal et al.(2006)]are neural-network language models in which words are represented as high dimensional real-valued vectors.These vector representations have recently demonstrated promising results in various tasks [Collobert and Weston (2008); Bengio, Schwenk, Senécal et al.(2006)] due to their superiority in capturing syntactic and contextual regularities in language.

Recent works in learning vector representations of words use neural networks [Mnih and Hinton(2008);Turian,Ratinov and Bengio(2010);Mikolov,Sutskever,Chen et al.(2013)].The outcome is that after the neural network model is trained,the word vectors are mapped into a vector space such that semantically similar words have similar vector representations.Distributed word representations draw more attention for better performance in a wider range of natural language processing tasks,ranging from speech tagging[Santos and Zadrozny (2014)], named entity recognition [Turian, Ratinov and Bengio (2010)], partof-speech tagging, parsing [Socher, Lin, Manning et al.(2011)], semantic role labeling[Collobert,Weston,Bottou et al.(2011)],phrase recognition[Socher,Lin,Manning et al.(2011)],sentiment analysis[Socher,Pennington,Huang et al.(2011)],paraphrase detection[Socher,Huang,Pennin et al.(2011)],to machine translation[Cho,Merri?nboer,Gulcehre et al.(2014)].Han et al.[Kim,Kim and Cho(2017)]proposed a method to create concepts by clustering word vectors generated from word2vec, and used the frequencies of these concept clusters to represent document vectors.

The distributed word vector learning mainly depends on word in the vocabulary and corpus,corpus collected is generally according to time ordered in topic related or event related.In this paper,we divide documents into several subsets,in order to preserve accurate proximity information among subset,a combination model based on strategy of optimization and regression,as an extension of distributed word vector is constructed.

The rest of this paper is organized as follows:Section 2 introduces prior research related to n-gram,CBOW model and Skip-gram model.Section 3 formally presents our approach in the integrated extension model for word vector representation.Two novel models CBOWOR and SkipGram-OR are proposed.Section 4 describes the experimental settings and experimental results.At last, we conclude the paper and discuss some future work in Section 5.

2 Related works

2.1 n-gram model

The goal of statistical language modeling[Bengio,Ducharme,Vincent et al.(2003)]is to learn the joint probability function of sequences of words in a language.This is intrinsically difficult because of the curse of dimensionality: a word sequence on which the model will be tested is likely to be different from all the word sequences seen during training.

Curse of dimensionality: For example, if one wants to model the joint distribution of 10 consecutive words in a natural language with a vocabulary V of size 100,000, there are potentially 10000010-1=1050-1 free parameters.

A statistical model of language can be represented by the conditional probability of the next word given all the previous ones,since

where wtis the t-th word,

Such statistical language models have already been found useful in many technological applications involving natural language,such as speech recognition,language translation,and information retrieval.

Following the above mentioned models, n-gram models construct tables of conditional probabilities for the next word and for each one of a large number of contexts,i.e.,combinations of the last n-1 words:

Bengio et al.[Bengio,Ducharme,Vincent et al.(2003)]proposed a neural network model to calculate formula(2),Feature vectors of words are learned based on their probability of co-occurring in the same documents.

The training set is a sequence w1,w2,··· ,wTof words belong to V,where the vocabulary V is a large but finite set.The objective is to learn a good model f(wt,···wt-n+1) =that can give high out-of-sample likelihood.The model is decomposed intothe following two parts:

1) A mapping C from any element i of V to a real vector C(i) ∈Rm.It represents the distributed feature vectors associated with each word in a vocabulary.In practice, C is represented by a|V|×m matrix of free parameters.

2)A function g maps an input sequence of feature vectors of words in context

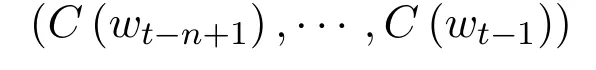
to a conditional probability distribution over words in V for the next word wt.The output of g is a vector whose i-th element estimates the probabilitshown in Fig.1.

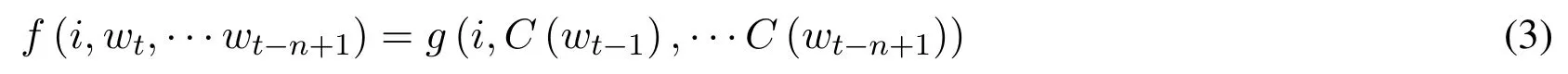
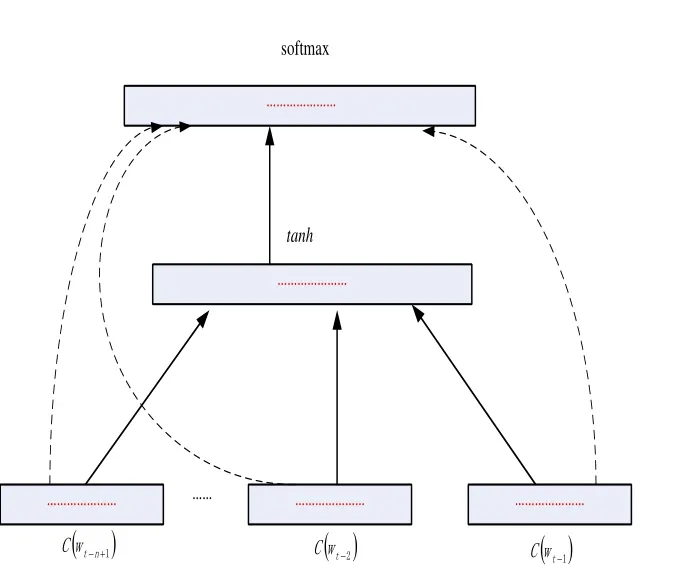
Figure 1: Neural architecture f(i,wt,··· ,wt-n+1)=g(i,C(Wt-1),··· ,C(Wt-n+1))

Training result is achieved by finding θ that maximizes a training corpus penalized loglikelihood:

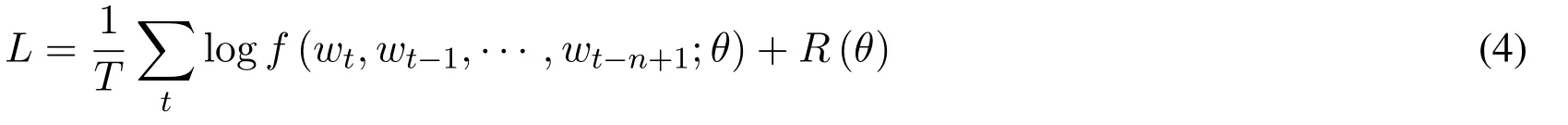
where R(θ)is a regularization term.R is a weight decay penalty applied to the weights of a neural network and to the matrix C.

The softmax output layer is calculated as follows:

yiis the unnormalized log-probability for each output word i, computed as follows, with parameters b,W,U,d and H:

where the hyperbolic tangent tanh is applied element by element,W can be optionally set to zero(no direct connections),and x is the word features layer activation vector,which is the concatenation of the input word features from the matrix C:

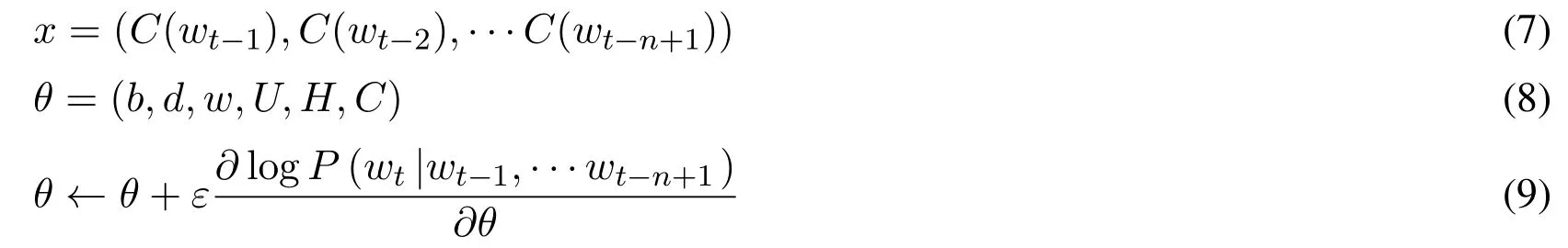
ε is the“l(fā)earning rate”.

2.2 The word vector model

Mikolov et al.[Mikolov, Sutskever, Chen et al.(2013)] introduced the CBOW and Skip-Gram model.Both models include three levels: input, projection and output (Fig.2 and Fig.3).The training objective is to learn word vector representations that can predict the nearby words well.

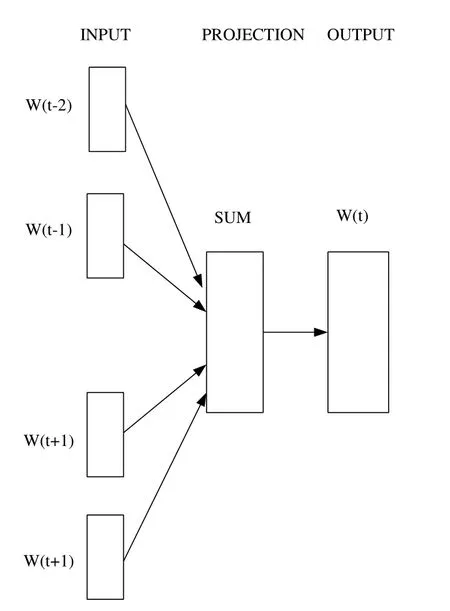
Figure 2: The CBOW model

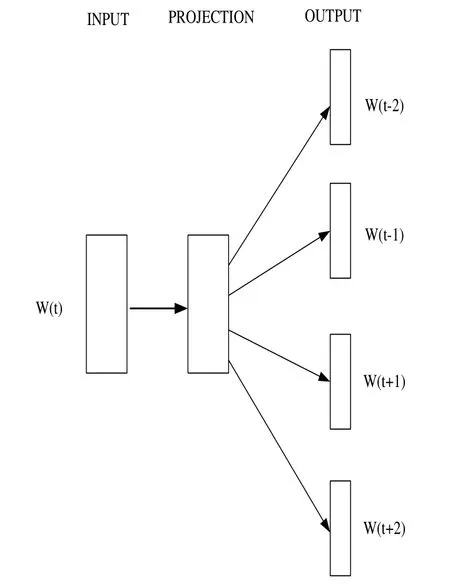
Figure 3: The Skip-gram model

Given a sequence of training words w1,w2,··· ,wT, the CBOW model is asked to maximize the following average log probability,

but the Skip-Gram model is asked to maximize the average log probability

where c is the size of the training context.The basic Skip-Gram formulation of p(wt+j|wt)is defined using softmax function as follows:

where vwtis input vector representation of word wt,andare output vector representations of words wt+j,wi.W is the number of words in a vocabulary.

There are many methods for visualizing the relationship between words vector representation.Fig.4 shows one way for terms' relevancy: two-dimensional PCA projection of the 1000-dimensional Skip-Gram vectors of countries and their capital cities [Mikolov,Sutskever, Chen et al.(2013)].It illustrates the ability of the model [Mikolov, Sutskever,Chen et al.(2013)] to automatically organize concepts and learn implicitly.Without any supervised information about what a capital city means during training are given before the mining relationships between them are obtained.

Figure 4: Country and Capital Vectors Projected by PCA[Kim,Kim and Cho(2017)]

Fig.5 shows another visualization method for clustering same word association, t-sne clustering method is used.“t-SNE”is a technique which visualizes high-dimensional data by giving each datapoint a location in a two or three-dimensional map.The technique is a variation of Stochastic Neighbor Embedding [Georey and Roweis (2002)] that is much easier to optimize,and produces significantly better visualizations by reducing the tendency to crowd points together in the center of the map.Stochastic Neighbor Embedding(SNE) starts by converting the high-dimensional Euclidean distances between datapoints into conditional probabilities that represent similarities [Kim, Kim and Cho (2017)].In t-SNE[Maaten and Hinton(2008)],it employs a Student t-distribution with one degree of freedom as the heavy-tailed distribution in the low-dimensional map.

As Fig.5 shown that words are represented in a continuous embedded space is very important.Various conventional machine learning and data mining techniques can be applied in this space to solve various text mining tasks[Cui,Shi and Chen(2016);Bansal,Gimpel and Livescu(2014); Xue, Fu and Zhan(2014); Cao and Wang(2015); Ren, Kiros and Zemel(2015)].Fig.5 also shows an example of such embedded space visualized by t-sne[Cui,Shi and Chen(2016)].The embedded words located in one circle represent the names of baseball players, the names of soccer players and the names of countries are separated in different clustering circle, and words similar meanings are located close.The words with different meanings are located far away.

2.2.1 Hierarchical softmax

The formula(12)is a full softmax model which is impractical because the cost of computing is proportional to W, which is often large(105-107terms).The hierarchical softmax is a computationally efficient approximation of the full softmax.The main advantage of hierarchical softmax is that instead of evaluating W output nodes in the neural network to obtain the probability distribution,it evaluates only log2(w)nodes.

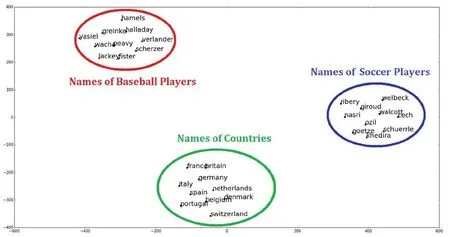
Figure 5: Embedded space using t-sne [Maaten and Hinton (2008);Kim, Kim and Cho(2017)]

Hierarchical probabilistic neural network language model was first proposed by Morin[Morin and Bengio(2005)],Mnih and Hinton[Mnih and Hinton(2008)]explored a number of methods for constructing a tree structure and ameliorated the effect on both the training time and the resulting model accuracy.Mikol et al.[Mikolov,Sutskever,Chen et al.(2013);Mikolov(2012)]used a binary Huffman tree,as it assigns short codes to the frequent words which results in fast training.

The hierarchical softmax uses a binary tree representation of the output layer with the W words as its leaves.For each word w located at the leaf,let n(w,j)be the j-th node on the path from the root to w,and let Len(w)be the length of this path,so n(w,1) = root and n(w,Len(w))=w.let child(n)be an arbitrary fixed child of inner node n,and let〈x〉be 1 if x is true and-1 otherwise,then the hierarchical softmax is defined as follows:

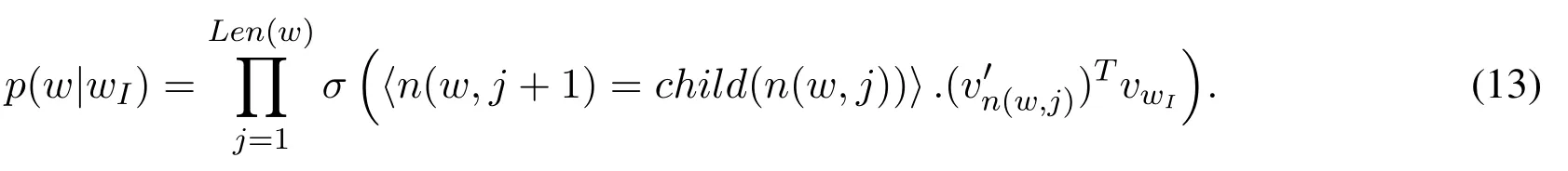
where σ(x)=1/(1+exp(-x)),the cost of computing log p(wO|wI)and?log p(wO|wI)is proportional to Len(wO),which on average is no greater than log W.

3 New learning model of word vector representation

We first divide training document into several relative subsets of document, the relative property may be considered as document collection of contextual feature and semantic feature.

Let Cp1,··· ,Cpnbe n subsets,V1(w),··· ,Vn(w)be corresponding distributed word vectors for word w generated from CBOW or Skip-Gram model.Let SAMT be a sampling set in the vocabulary for topic words,in order to preserve accurate proximity information among subsets, we consider a regression model as an extension of distributed word vectors.The new learning model for distributed word vector representation is described as the following optimization problem and regression strategy.

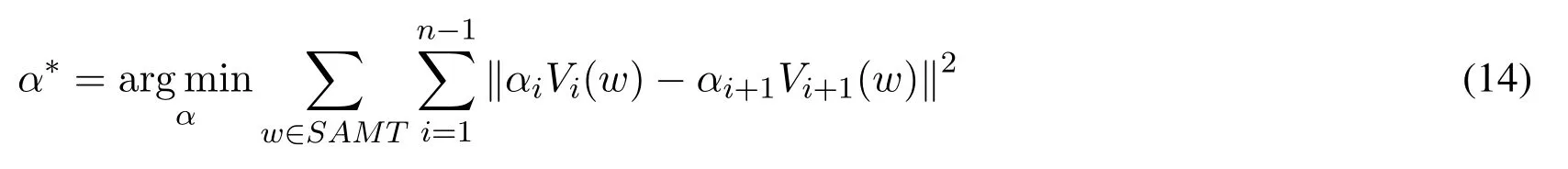
Step 2.reconstruct word vector for each word w

Fig.6 shows the integrated extension model for distributed word vector representation.

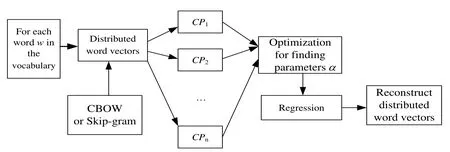
Figure 6: The new generation model of word vector representation

4 Experiments

4.1 Task description

Our task is to develop a new method for generating word vectors and verify its efficiency on actual document dataset.The new generation model of word vector includes two submodels, one is based on the combination of CBOW [Mikolov (2012)] and our regression with optimization strategy, we denote CBOW-OR model, and the other is based on the combination of Skip-Gram[Mikolov(2012)]and our regression with optimization strategy,denote SkipGram-OR model.In the following experiments,we divide documents into three sub-documents, and on the premise of sharing same vocabulary, same word vectors are trained respectively on three subsets with same dimension.The optimization and regression methods are used to integrate the three vectors into a vector,which is regarded as the word vector of the word.

4.2 Dataset description

The dataset we are using is text8,which is download using Google word2vector.The size of the corpus is 100 MB, vocabulary size is 71291 in documents, some auxiliary words have been removed,for example,a,the,is,and so on.And some rare words are removed.In addition, the whole documents contains 4406976 words.Using method, we divide the documents into three parts in size: 36.6 MB, 36.6 MB, 26.8 MB.We name these three sub-documents as text8_1, text8_2, and text8_3.The same word is trained separately on the 3 sub-documents to obtain 3 vectors, and then a word vector is obtained by using the optimization and regression mentioned above.

4.3 Evaluation mode

In order to test the effect of our method, we design two sets of comparative experiments,one is to measure Euclidean distance of the vector in two different vector spaces with same dimension,the other is to measure cosine distance of the two word vectors in each vector space.

Three groups of experiment are conducted according to different SAMT in Eq.(14), for Tabs.1 and 3, SAMT={cat, China, computer, dog, exam, hospital, Japan, nurse, school,software},for Tabs.4 and 6,SAMT={car,children,country,driver,hospital,nation,nurse,parent,school,students},for Tabs.7 and 9,SAMT={army,chef,friend,fruit,gentlemen,ladies, partner, restaurant, soldier, vegetables}.Four kinds of word vector space are respectively generated by CBOW,Skip-Gram,CBOW-OR and SkipGram-OR.The last two models is proposed in this paper.

In Tabs.1, 2, 4, 5, 7, 8, we compare the Euclidean distance of the vector learned for the same word under different vector spaces.We know that a vector can be represented as a point in vector space.Since the dimension for each words of vector space is same, we can compare the Euclidean distance of a word in different spaces.We can test the relation between the Euclidean distance of multiple key words in any two different vector spaces,in order to test the structure consistency of different vector spaces.

Since the cosine distance of the two similar word vectors that are trained should be relatively large, the semantic relationship between words is similar in an article.In other words,the probability of simultaneous occurrence of two words should be large,such as cats and dogs, hospitals and nurses, school and students, etc.So in the Tabs.3, 6, 9, we compare the cosine distance between the vector pairs of the same set of word pairs, which are obtained under three different learning mechanisms respectively,as a criterion for evaluating the vector of words.

Tab.1 to Tab.9 show some interesting properties: Tabs.1, 2, Tabs.4, 5, Tabs.7, 8 show that the words vector space for Skip-Gram and SkipGram-OR keep the same structure property in Euclidean distance.Tab.3 shows that there exists more accurate cosine distance between two words using SkipGram-OR model than other models of CBOW,CBOW-OR and Skip-Gram,meanwhile,Tabs.6,9 show that there exist more accurate cosine distancebetween two words by using CBOW-OR model than other models of CBOW,SkipGram-OR and Skip-Gram.

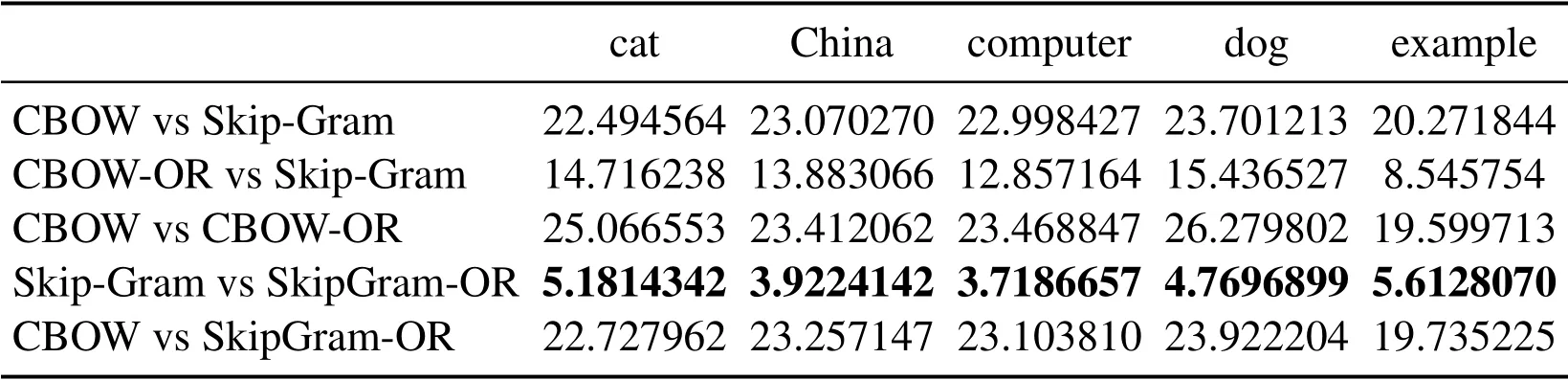
Table 1: Euclidean distance of the vector learned from the same word under different methods

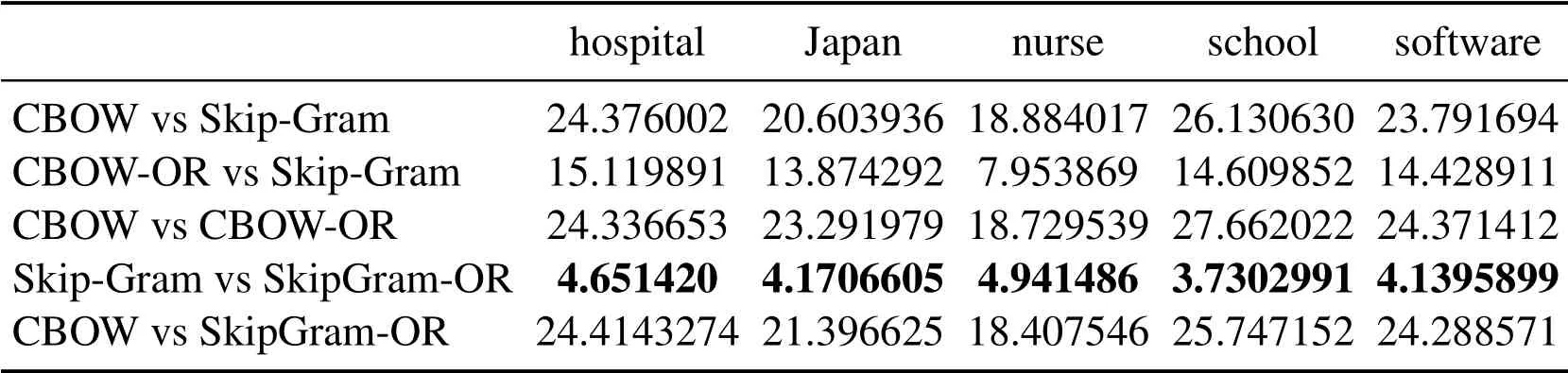
Table 2: Euclidean distance of the vector learned from the same word under different methods

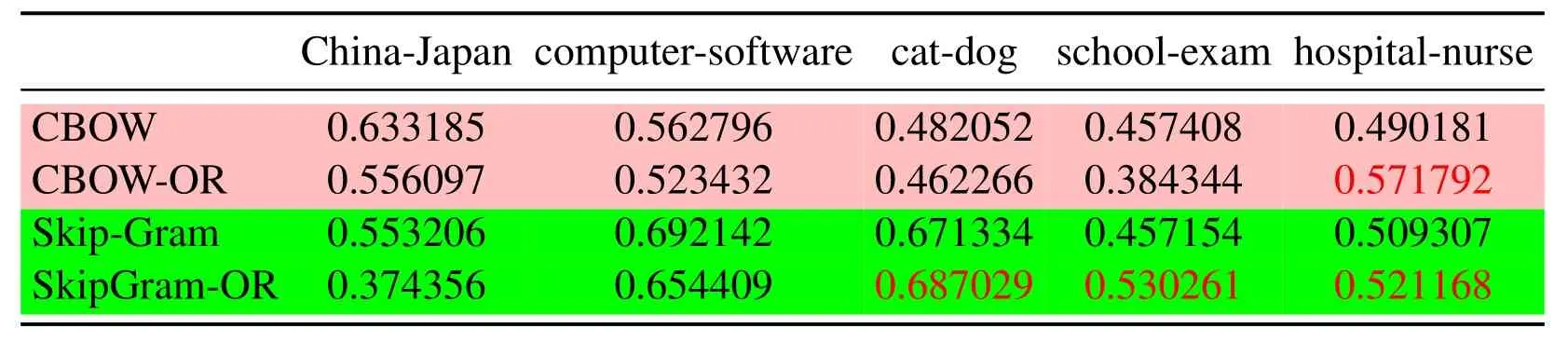
Table 3: The cosine distance of the two word vectors

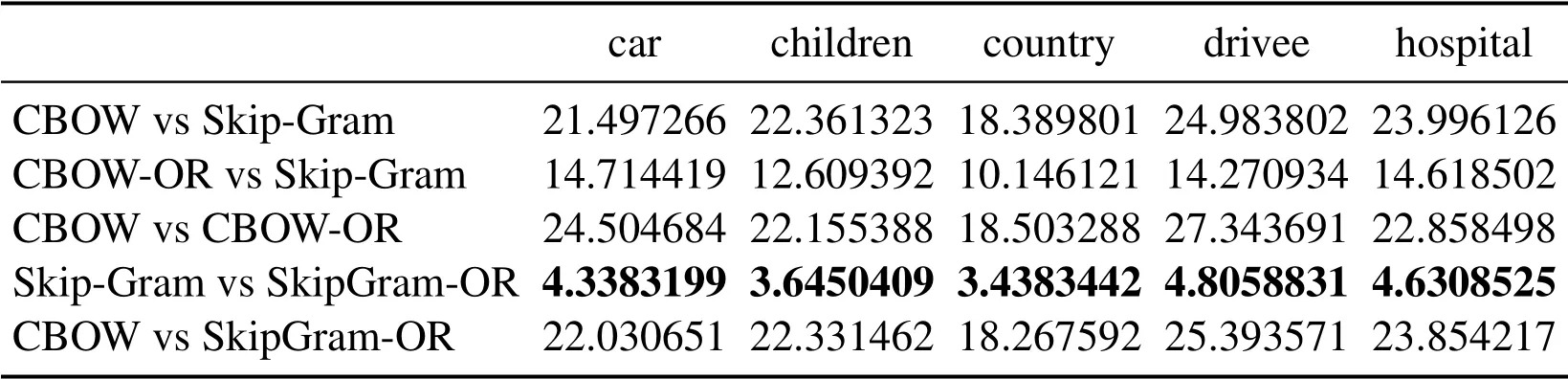
Table 4: Euclidean distance of the vector learned from the same word under different methods

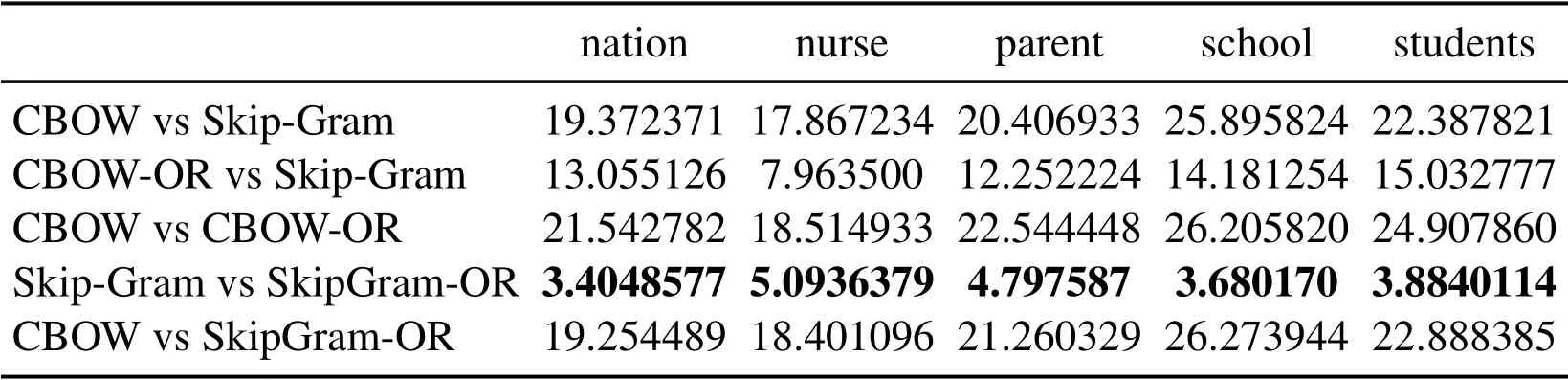
Table 5: Euclidean distance of the vector learned from the same word under different methods

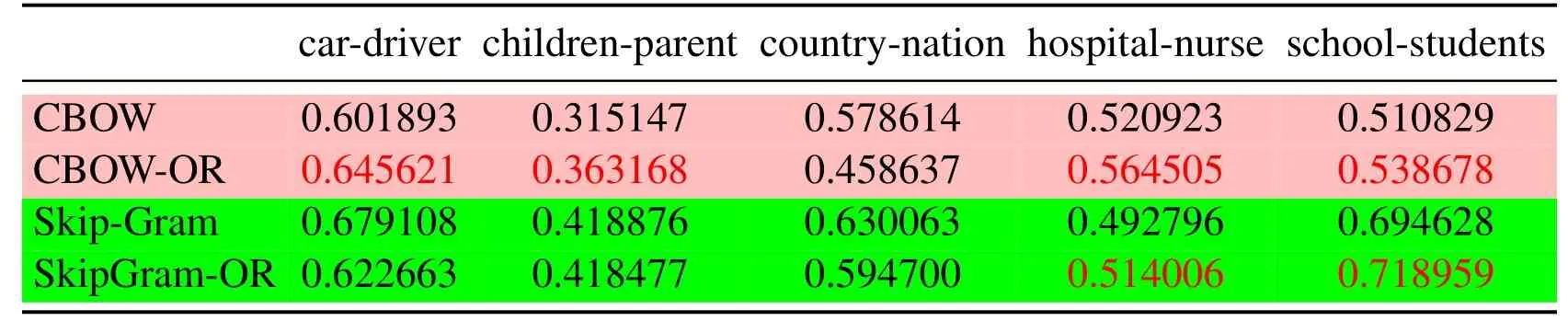
Table 6: The cosine distance of the two word vectors

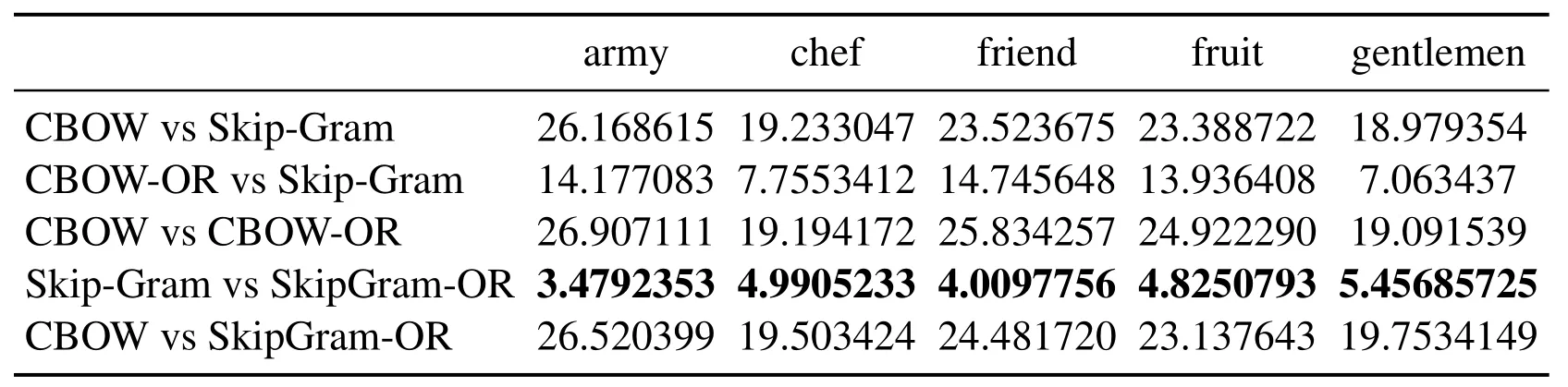
Table 7: Euclidean distance of the vector learned from the same word under different methods

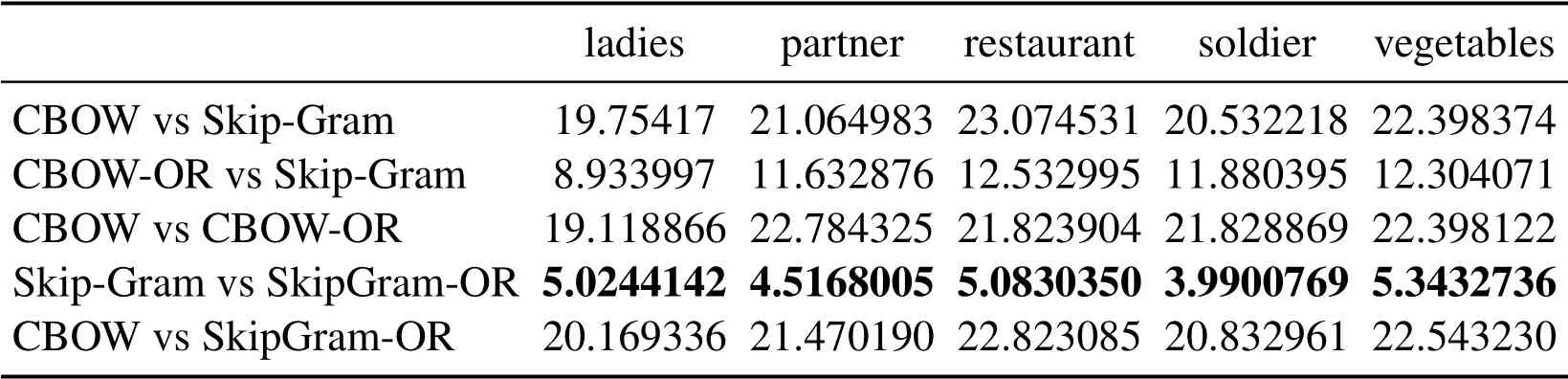
Table 8: Euclidean distance of the vector learned from the same word under different methods

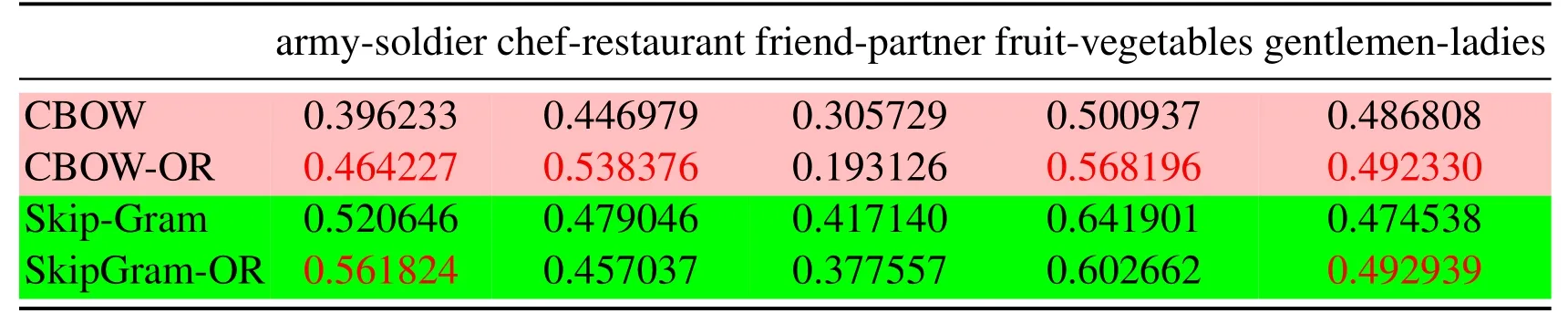
Table 9: The cosine distance of the two word vectors

By combining Tabs.3, 6, 9, we get the synopsis for 15 different words towards four different models.Fig.7 shows that the model SkipGram-OR keeps higher performance for retrieval the relative words-pair as a whole.

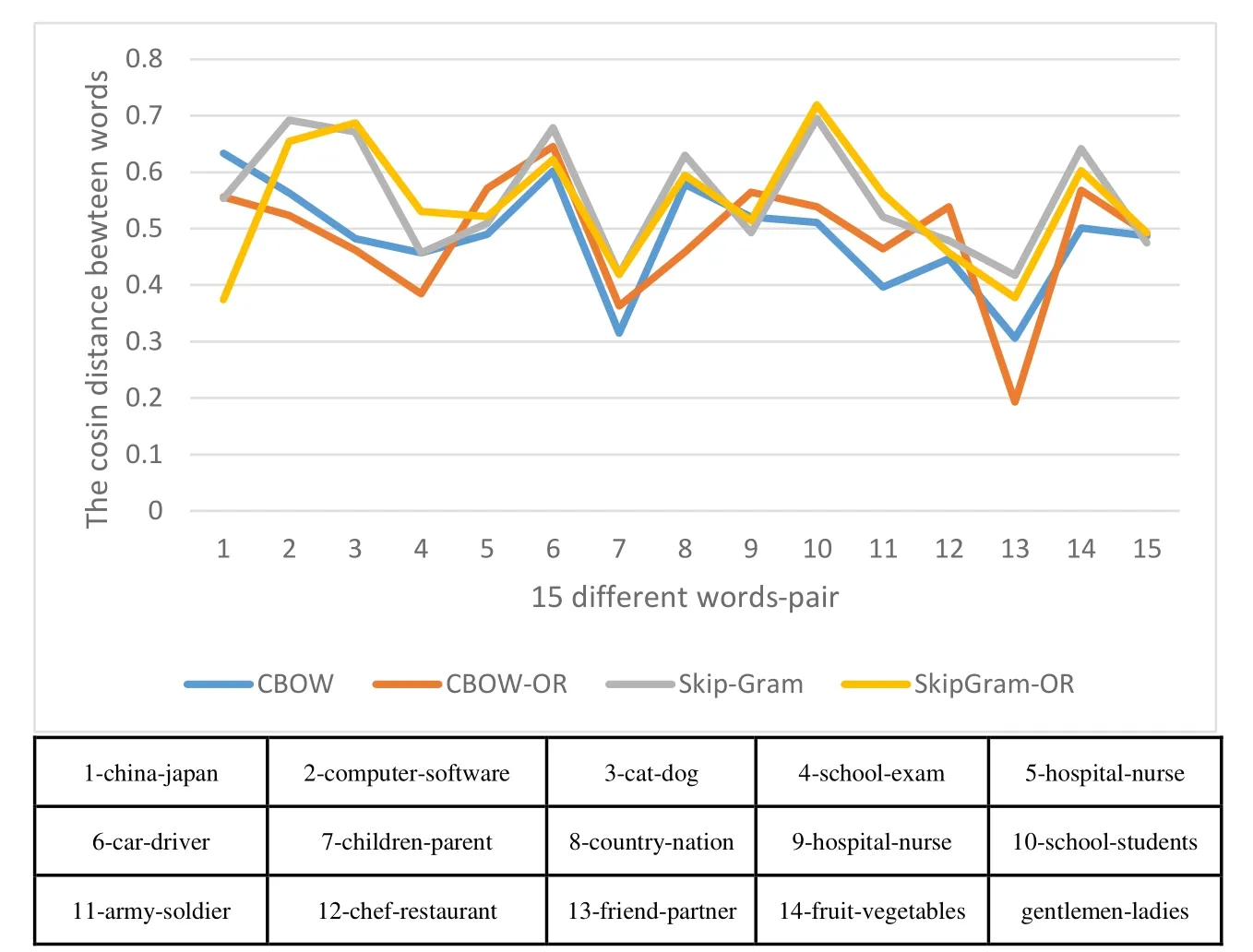
Figure 7: the comparative result of four models for 15 different words-pair

5 Conclusions

We develop two kinds of models for generating words of vector:CBOW-OR and SkipGram-OR.The key strategy for these two models is using optimization in contiguous training documents and regression method in combination of vectors.CBOW-OR and SkipGram-OR can be performed in parallel.Experimental results show that for some words pair,the cosine distance obtained by the CBOW-OR or SkipGram-OR model is generally larger and is more reasonable than CBOW and Skip-Gram.

We also achieved exciting results.The Euclidean distance between the vectors of the same word learned under different mechanisms is nearby.It can be seen that the vector space obtained by different models has some consistency.That is, the Euclidean distance of different word vectors in any two vector spaces is approximately the same.Especially, we also find that the vector space for Skip-Gram and SkipGram-OR keep the same structure property in Euclidean distance.

Based on the inherent parallel in generating words of vector and semantic validity in words pair, the proposed models in this paper can be expected to apply in large-scale information processing.

Acknowledgement:The authors would like to thank all anonymous reviewers for their suggestions and feedback.This work Supported by the National Natural Science Foundation of China (No.61379103,61379052), the National Key Research and Development Program (2016YFB1000101) the Natural Science Foundation for Distinguished Young Scholars of Hunan Province (Grant No.14JJ1026), Specialized Research Fund for the Doctoral Program of Higher Education (Grant No.20124307110015).