Jing Wang , Xiaohe Qiu and Yuanfei Tu

Abstract: The MDS-MAP (multidimensional scaling-MAP) localization algorithm utilize almost merely connectivity information, and therefore it is easy to implement in practice of wireless sensor networks (WSNs).Anisotropic networks with energy hole, however, has blind communication spots that cause loss of information in the merging phase of MDSMAP.To enhance the positioning accuracy, the authors propose an MDS-MAP (CH) algorithm which can improve the clustering and merging strategy.In order to balance the effect of energy consumption and the network topology stabilization, we present a weighted clustering scheme, which considers the residual energy, the degree of connectivity nodes and node density.As the original MAD-MAP method poses a limitation of merging condition, the authors relax the merging requirement and present a heuristic estimation method for lost connectivity over energy holes.Simulation results show that the improved MDS-MAP (CH) localization algorithm has achieved higher localization accuracy, better-balanced energy consumption and stronger network robustness.

Keywords: Wireless sensor network, localization, MDS-MAP, clustering, merging strategy, heuristic method.

1 Introduction

WSNs (Wireless Sensor Networks) are ad-hoc networks composed of sensor nodes with limited computational and communicational capabilities.Sensor nodes are usually randomly scattered into the filed.Thus it is necessary to report data with geometrical information.Nowadays, localization of sensor nodes in WSN has become a fundamental and essential service which benefits many industrial and civilian cyber-physical system applications, such as environmental monitoring, industrial control and battle fields [Adissi, Lima, Gomes et al.(2017); Sundararajan, Redfern, Schneider et al.(2005); Perumal, Utharaj and Christo (2014)].Although localization is crucial in determining the source of triggering events, over complex algorithms are not supported by the light weight process unit in the network.Therefore, extensive research has been focusing on designing localization algorithms that are energy and cost efficient.

Mounting GPS on each sensor in the network is an easy solution but too expensive to be feasible in practice.GPS receivers have degraded performance in indoor places and dense urban areas [Sahu, Wu and Sahoo (2017); Tashnim, Chowdhury, Vijay et al.(2016)].A typical scenario is that there are only a few nodes equipped with position-aware device and those nodes are referred to as anchors.The localization of other nodes is accomplished by its interaction and information exchange with anchors.Various existing localization schemes can be classified as centralized or distributed.Centralized algorithms utilize a central computing unit to calculate each node’s position based on the information collected through the network [Fang, Jiang and Nan (2016); Carmelo, Mauro, Enrico et al.(2018)].These techniques are usually more accurate because they use global modeling, but the cost is the heavy computation overhead and communication bottleneck.While in distributed approaches, the process resides in a subset of the global graph, which is much more practical regarding lower energy consumption and communication coverage cost.Multidimensional scaling (MDS) is a typical centralized localization algorithm which uses simple network connectivity to localize sensor nodes.It is regarded as a practical scheme because sophisticated position tracking- devices are avoided and only a few anchors are enough for final graph adjustment.

The classical MDS algorithm is a means aims at visualizing the placement of a set of objects in N-dimensional space based on the between-object distances, or dissimilarities.It is widely used in many application areas as a set of information visualization techniques.Recent research tends to develop distributed MDS algorithms [Shang and Ruml (2004); Saeed and Nam (2016)] and the benefit is much more noticeable in largescale networks.Shang et al.[Shang and Ruml (2004)] presented the MDS-based localization algorithm called MDS-MAP (P), which uses patches of relative maps for local positioning and then merge those maps into a global one.The merging can be executed in distributed fashions and this leads to more balanced computation.Besides, it works well on irregular networks.

In practice, communication holes caused by power exhaustion are often found in the unbalanced network.In this investigation, we propose a cluster-based MDS localization algorithm called MDS-MAP (CH) for WSN with energy holes.We present a better clustering strategy which balances the energy consumption and network topology stability.We also propose an improved heuristic merging scheme to compensate previous existing merging restrictions that plague anisotropic network with energy holes.The contributions of this study are summarized as follows:

· We develop a clustering strategy as a segmentation technique that is better at balancing the energy consumption and topology over the network.This clustering strategy also provides an excellent solution for cluster-head selection in an energy unbalanced network.The strategy utilizes a competition to choose the best candidate node based on node residual energy, connectivity and edge-degree.This election mechanism leads to a better-balanced network and well-chosen cluster-heads as subprocessing centers.

· A heuristic algorithm is proposed to compensate connectivity information for merging relative maps.The algorithm is implemented on the boundary of two clusters where communication is blocked over energy holes and it constructs virtual connectivity close on the border of the obstructed area so that a relaxed merging condition is satisfied.

The rest of this paper is organized as follows: In Section 2, background and related works are summarized.In Section 3, the motivation and details of the proposed MDS-MAP (CH) are presented.Section 4 presents the experimental results and performance evaluation.Finally, we state the conclusion of this paper and thoughts of future work in Section 5.

2 Background and related work

The classical MDS-MAP based localization algorithm was developed in the past decades and the idea is to take an input of between-nodes distance matrix and output a coordinate matrix by minimizing a loss function.The popular MDS-MAP was proposed in Hightower [Hightower (2001)] and the localization method was based on multidimensional scaling (MDS).In this centralized approaches, the final network graph requires a transformation into absolute coordinates over the anchors.Shang et al.[Shang and Ruml (2004)] proposed the distributed MDS-MAP (P) which aims at improving the performance by avoiding the inaccurate shortest path.Shi et al.presented a heuristic MDS algorithm in Shi et al.[Shi, Meng, Zhang et al.(2017)], which explores virtual nodes to construct the shortest paths between nodes and this can be a distinct advantage in anisotropic networks.

There are two drawbacks of the classical MDS-MAP algorithm.Firstly, poor positioning results are shown for anisotropic networks.Secondly, the merging strategy restriction is too strict.In Shang et al.[Shang and Ruml (2004)], MDS-MAP (P) uses paths within 2 to 3 hops to estimate the distances between nodes, which can cause significant errors when merging nodes are out of the communication range.Jia et al.[Cheng, Qian and Wu (2008)] proposed an improved merging strategy for relaxing the previous restrictions to more general conditions.

A relative map segmentation method based on rigid subset is proposed in Yu et al.[Yu, Zhou and Zhang (2017)] to overcome the flip ambiguity problem in merging, which adopts the graphic rigidity theory for unique merging solution.Another segmentation strategy is proposed by Kim et al.[Kim, Woo and Kim (2007)], which only consider local maps composed of nodes within the reliable communication range.Therefore, the accuracy is enhanced, but the merging condition is neglected.Clustering has been considered an effective method to distribute computation overhead and degrade the complexity.Weighted clustering further helps with decision making [Edwards, Stillwell and Seaver (1981)].A number of cluster-based MDS algorithms are available in recent literature [Biljana, Danco and Andrea (2008)], [Minhan, Minho and Hyunseung (2012)] and they have proven this technique outperforms MDS in terms of accuracy especially in irregular networks.Saeed et al.[Saeed and Nam (2016)] proposed an algorithm for a cognitive network that uses the fuzzy C-means clustering technique to reduce shortest path error and the computational complexity is distributed into clusters.Chen et al.[Cheng, Qian and Wu (2008)] proposed an energy based weight-clustering which improved clustering formation by taking energy efficiency into consideration.

2.1 Summary of MDS-MAP

In this subsection, we briefly summarize the 3 phases of the MDS-MAP based localization algorithms as follows:

Phase 1:A distance matirx for the MDS is constructed within each cluster based on the shortest paths between nodes.

The distance matrix, which is also called dissimilarity matrix D, can be estimated with algorithms, e.g., Dijkstra shortest path.Assume that there are n nodes lying on a 2-D plane.Then distance matrix D2(X) is constructed with squa value of distance measurements, where X denotes the coordinate estimation matrix.D2(X) is expressed as:

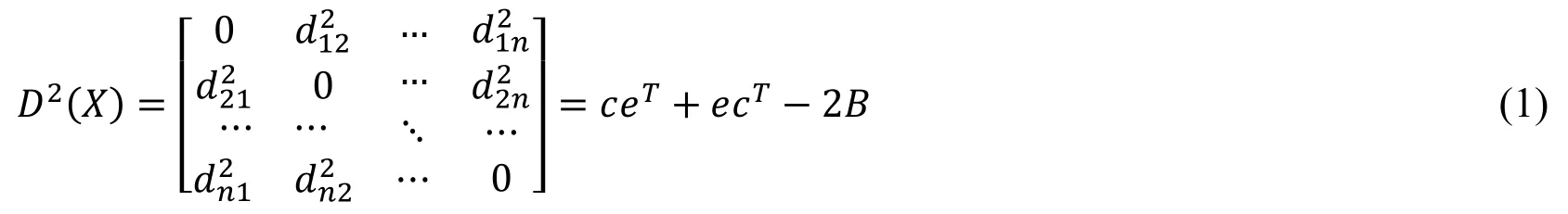
where dijrepresents the Euclidean distance between node i and node j, e=(1,1,…,1)T, matrix

Apply a decantation process with matrix J=(I-n-1eeT):

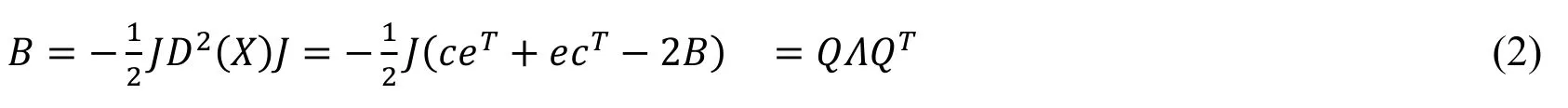
Perform singular value decomposition on matrix B:

Phase 2:The MDS utilizes the distance matrix to generate relative maps.The relative coordinates can be represented by

Phase 3:Relative maps are merged into the absolute map with sufficient anchors.Various merging strategies can be used to stitch patches of local maps to form a global relative map.Finally, build the absolute map by performing a transformation process on the relative map:

where α is the scaling factor and t0is the translation coefficient, and R(?) is the rotation and translation matrix.xs,iis the relative coordinates of node i before merging.After all clusters are merged, the relative coordinates of the nodes can be adjusted into the global map by anchor nodes, where each node i gets its absolute coordinates at x0,i.

2.2 Merging strategy

In phase 1 of MDS-MAP framework, the network is divided into segments or clusters.Those local patches should be stitched together in merging phase 3, using information on the borders or overlapping areas.Merging can only be done under certain conditions.Yu et al.[Yu, Zhou and Zhang (2017)] utilizes the rigid subset characteristic to avoid the ambiguity in local map construction and merging, which implicitly requires a sufficient number of common nodes and connectivity between local graphs.Merging restriction analysis has been a neglected problem in MDS-MAP (P) related algorithms.In Kim et al.[Kim, Woo and Kim (2007)], the paper proposed a merging method that constructs the global map with local maps at a common node.This algorithm requires three common nodes between every two segmented maps during merging.Most cluster-based algorithms [Biljana, Danco and Andrea (2008); Minhan, Minho and Hyunseung (2012)] also require adequate information within communication range on the boundary.Assuming that there are N nodes deployed in a 2-D plane and for each node i ∈S, where node set is S={1,2,…,N}.The distance measurement between node i and j is denoted as dij.A common node merging condition can be summarized as follows: Assume that two cluster nodes sets are C1and C2and the set of common nodes is Q =C1∩C2, and the set of non-common nodes of C1and C2are represented as FC1=(C1∪C2)C2and FC2=(C1∪C2)C1.Previous work Saeed et al.[Saeed and Nam (2016)] suggests that two clusters can be merged only when the size of the common node set Q satisfies:|Q|≥3.Dan et al.[Jia, Li, Wang et al.(2016)], studied the merging condition in localization algorithms under MDS-MAP framework.In this investigation, the authors conducted a thorough analysis and the relaxed the merging requirements.The analysis suggests that when |Q|＜3, additional distance information dabshould be provided, where node b ∈FC1, and node a ∈FC2, then C1and C2can be merged.

Based on the rigidity theory, we drew the following conclusions.Assuming that in mdimensional space and the size of non-collinear common node set is |Q| , we can summarize the two relaxed merging conditions as follows:

· Condition 1: If |Q|≥m+1 , two maps can be uniquely merged.The rigid subset [Yu, Zhou, Zhang (2017)] strategy falls into this category.

· Condition 2: If |Q|＜m+1, additional connectivity information has to be found to form a local rigid boundary.In a 2-D plane there requires a number of (m+1-|Q|) connectivity.

Merging conditions can be illustrated by Fig.1(a): In the 2-D space, there have to be at least 3 common nodes between two clusters to meet the merging condition [Jia, Li, Wang et al.(2016)].Fig.1(b) shows that if the number of non-collinear common nodes is less than 3, there has to be some connectivity information for the two clusters to merge into a unique global formation.Moreover, Fig.1(c) shows that if there is no common nodes, there has to be at least three known connectivity (For example: dA1B1, dA1B2, dA2B3).

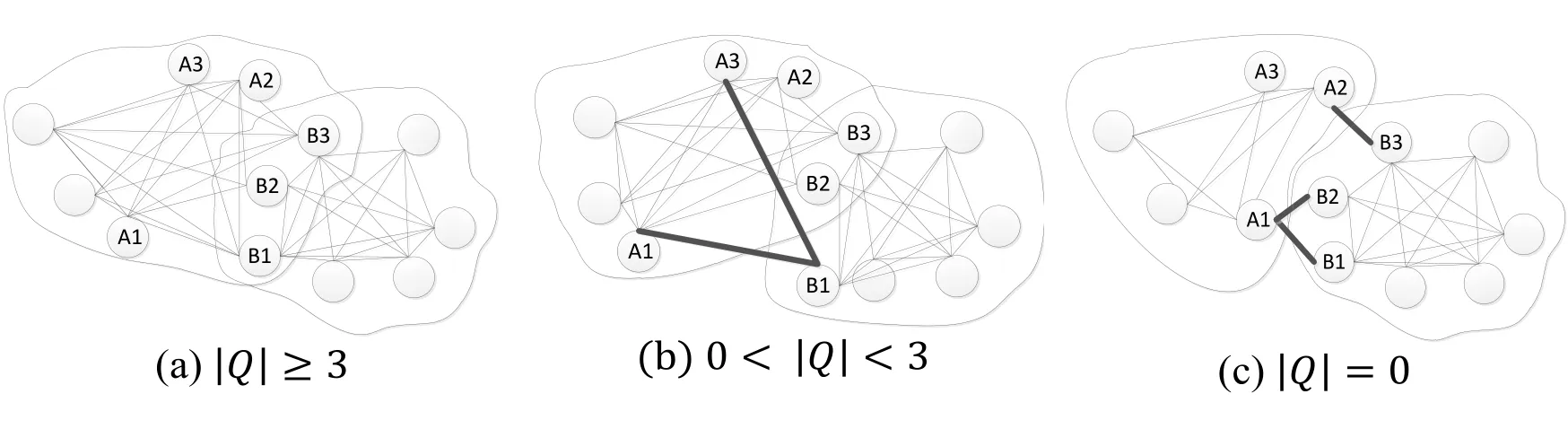
Figure 1: Inter-cluster nodes

In an anisotropic network, energy holes often block communication over the border, which causes loss of common nodes and connectivity information.In order to solve this problem, a heuristic method of distance estimation is proposed in Section 3.3 to compensate the merging rules.

2.3 Network model

Irregular network topology can obviously degrade the performance of MDS-MAP algorithms.The authors investigate the energy level and network topology characteristics of anisotropic networks.In this paper irregular specifically refers to networks with energy holes caused by battery drainage.The network model and parameters used in the proposed algorithm can be described as follows:

N=Total number of source nodes on a 2-D plane,

Ri=Communication range of sensor node i(m)

Di=Average node degree of senor node i (number of connected neighbors)

Edge(i)=Edge degree of sensor i (how far away the sensor is close to the edge of the network)

EC=Energy cost of signal reception in one transmission

Si=Residual energy level of the node i

Tab.1 lists other parameters used for the simulation of the research.In the study, sensor nodes are deployed in a two-dimensional square area.We assume that each node has an adjustable communication range Rito be more energy efficient.The degree of connectivity Diis dependent on the deployment of the network, which directly affect the network density.Edge degree can be a decent measurement of how close a node is to the local geometric center (or how far away it is to the edges).Nodes on the edge should not be favored as cluster heads because the sub process unit should lie in the center to balance resources in each local map.

Fig.2 shows an anisotropic network with holes which signal does not pass through and no nodes can be sensed within communication range.A local O-shaped area is therefore formed and the distance estimation using shortest path algorithm has to be done with a detour (Fig.2(b)).The authors used cluster-based graph segmentation method that considers energy level as a major factor so that network hole usually lies on the boundary between clusters.Therefore the inter-cluster communication issue needs to be addressed in the merging phase of the proposed MDS-MAP algorithm.Other parameters used in simulations are listed in Tab.1.

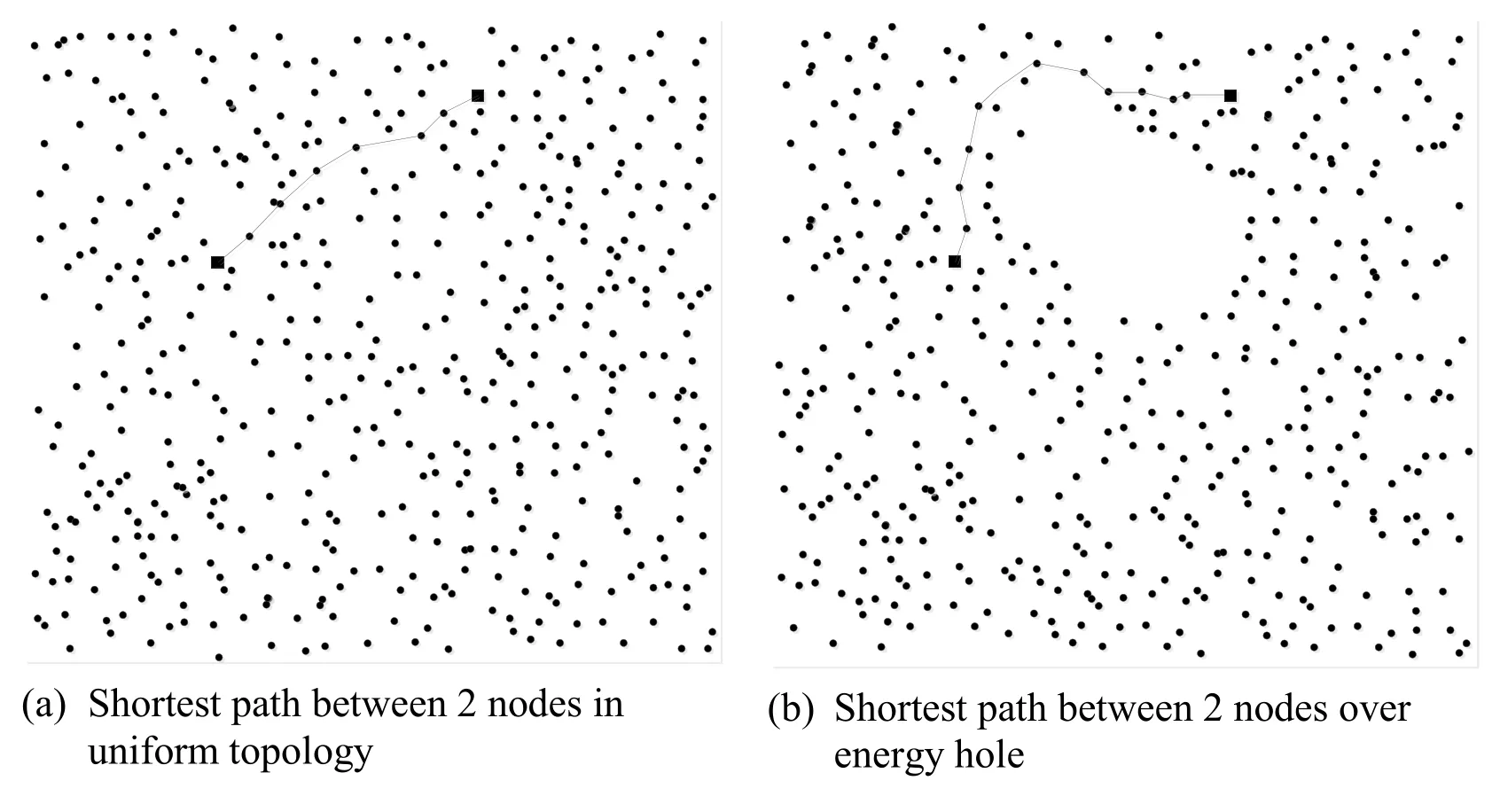
Figure 2: Shortest path error caused by energy hole

3 The proposed algorithm MDS-MAP (CH)

3.1 Motivation

The goal of this research is to investigate an energy efficient MDS-MAP localization algorithm for WSN with energy holes.The motivation of our research is that firstly, in most circumstances, energy holes are caused by unbalanced resource allocation.The network patch segmentation scheme should consider the distribution of network resources as well as topology stability.Therefore, we consider a weighted cluster head selection method that considers multiple factors so that the selected cluster head can perform better as the local process unit.

Secondly, energy holes cause blind area on the inter-cluster boarders, where two clusters need to be merged into the relative map in the third phase of MDS-MAP algorithms (Section 2.1).In existing algorithms, the perquisite merging condition requires a sufficient number of anchor nodes [Jia, Li, Wang et al.(2016)].This merging condition demands a large communication coverage overlapping area between two clusters, where the signal transmission, however, is often blocked by the energy holes.Thus, we present the heuristic algorithm to compensate the inter-cluster common information for merging purpose.

3.2 Weighted cluster-head selection scheme

Clustering technique helps to distribute and to degrade the computational complexity.Exiting clustering or cluster head selection strategy that considers only either graph partitioning or energy consumption often causes data redundancy, estimation error or high communication costs.When implementing MDS-MAP in energy unbalanced network, both network topology and energy consumption level are significant factors.Cluster head plays an important role in relative map formation.Here we take into consideration the connectivity, residual energy, and edge-degree for cluster head election.

The degree of a node can be described as the number of its neighbors within transmission range.To save resources of network bandwidth, the deployment of nodes in each cluster should not exceed a certain number, which means that the average degree of nodes connectivity is bounded.If the node degree is too large, there will be a communication bottle neck in the network, while if the node degree is too small, there will be a waste of network bandwidth resources.

The sum of the distance of the node i with its neighbors within the range can be calculated as:

Where dijis the distance between node i and node j.

The degree of all nodes is measured by degree-difference.The degree-difference of the node is expressed as:

Where d represents the average degree of nodes.

Normalize the degree-difference:

In the wireless sensor network, a node with a smaller degree-difference means evener distribution around it and it is more likely to be elected as a cluster head.The battery power is largely consumed by signal transmission and amplification.To formulate the energy cost of signal reception in one transmission, we use the wireless communication consumption model [Arumugam and Ponnuchamy (2015)] expressed as：

The energy consumed by nodes in each cluster can be expressed as:

We assume that node i is elected as a cluster head in the process of data collection, the total energy consumed in the cluster in one unit time is:

where, Eelecrepresents the energy consumed to send or receive 1-bit data.Efdenotes the energy consumed by the node to fuse 1-bit data.εfsindicates the amplification factor of the amplifier.n indicates the number of neighbor nodes and k is the length of the data packet, N denotes the number of nodes in the network, and H represents the number of cluster heads.The number of nodes in each cluster is represented by N/H.

Assuming that the initial cluster energy is Ei, the remaining energy Eliin the cluster at time t can be expressed as:

Higher residual energy level of the node i means the node fits cluster head better.Sidenotes the normalized value of the residual energy:

Usually, the cluster head should be in the center of the cluster, which can be measured by edge-degree [Anchao and Guifen (2017)].The edge degree is a measurement of how far away one node is to the center, or how close it is to the edge.The distance between each node with the nearest anchor node is recorded as dis(i), and the farthest one is recorded as dismax.

The overall weight parameter, considering degree-difference, residual energy, and edge degree is formulated as:

w1, w2and w3are the normalized weights of each index.

The clustering procedure is conducted as the following steps:

· Wireless sensor network battery power level are initialized.Each sensor node calculates its energy consumption;

· Within the transmission range Rm, each node sends message of the residual energy, hop count and network ID number to its neighbors.Meanwhile, the node receives the information and put it in the neighbor table;

· With the distance measurements obtained by RSSI values, degree-difference φiand the remaining energy Eli, and the normalized edge-degree edge(i) are calculated;

· Adjust the weights for each factor according to the scenario.The node with the highest weight among all adjacent nodes is elected cluster head (the number of nodes in the cluster should be more than 4 and each node is connected to each other).

After cluster head is selected, clustering can be done by taking in nodes within two hops distance away from the cluster head.After the clustering is done, the local maps are segmented and localization can be calculated using MDS-MAP by the cluster head.

3.3 Heuristic merging strategy

This section presents the improved heuristic strategy that helps two clusters merge when the energy hole on the boundary blocks necessary information.The previous merging scheme requires a sufficient number of common nodes in this phase.However, in an anisotropic network, energy holes often block the communication between clusters and neither the number of common nodes or distance measurements are enough for merging (as shown in Fig.3).On the other hand, using the Dijkstra method to calculate the shortest path causes a detour around the hole and the approximation will result in an aggregation of errors.Alternatively, we propose a heuristic method to explore virtual connectivity and calculate the Euclidean distance to compensate the merging condition.

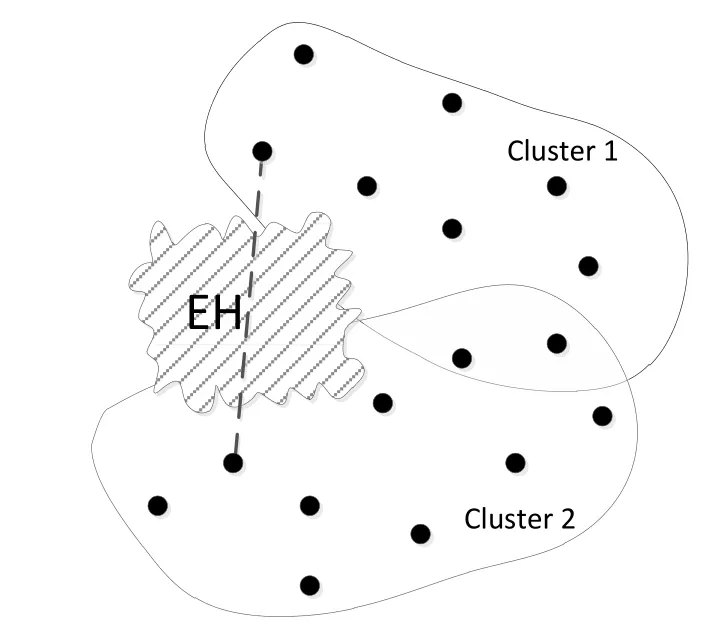
Figure 3: Energy hole blocks communication between two clusters

Fig.3 shows an example of an energy hole, denoted as EH, on the border of two merging clusters.There are only two common nodes in the overlapping area.As described in Section 2.2, in a 2-D plane if only two or less common nodes are found, the relaxed merging condition requires additional connectivity to be measured for two clusters to merge.

A a heuristic method to solve this problem in the relaxed merging condition is proposed.As shown in Fig.4, we consider there is an energy hole lying between two clusters C1and C2.Sensor node s1∈ C1, s2∈ C2and d3is unavailable because of the energy hole.c1∈ C1∩C2is one common node in the overlapping area of two clusters.d1=|s1c1| and d2=|s2c1|, therefore so s2should be lying on the arc of circle CS2between s3and s3′, where CS1∩CS2={s3,s3′}.

Now we explore the possibility of compensating a virtual connectivity d3.As shown in Fig.4, we consider an estimation of distance measurement d3required for merging condition when common nodes are not sufficient.And the equation can be expressed as:

As we can see the angle α between s2c1and s3c1, and the angle β between s3c1and s4c1, s4is where d3= d1+d2should satisfy: α ＜180°.Otherwise, if α ＞180°.Then, s1, s2′is not blocked and can be measured.Therefore, the equation can be expressed as:

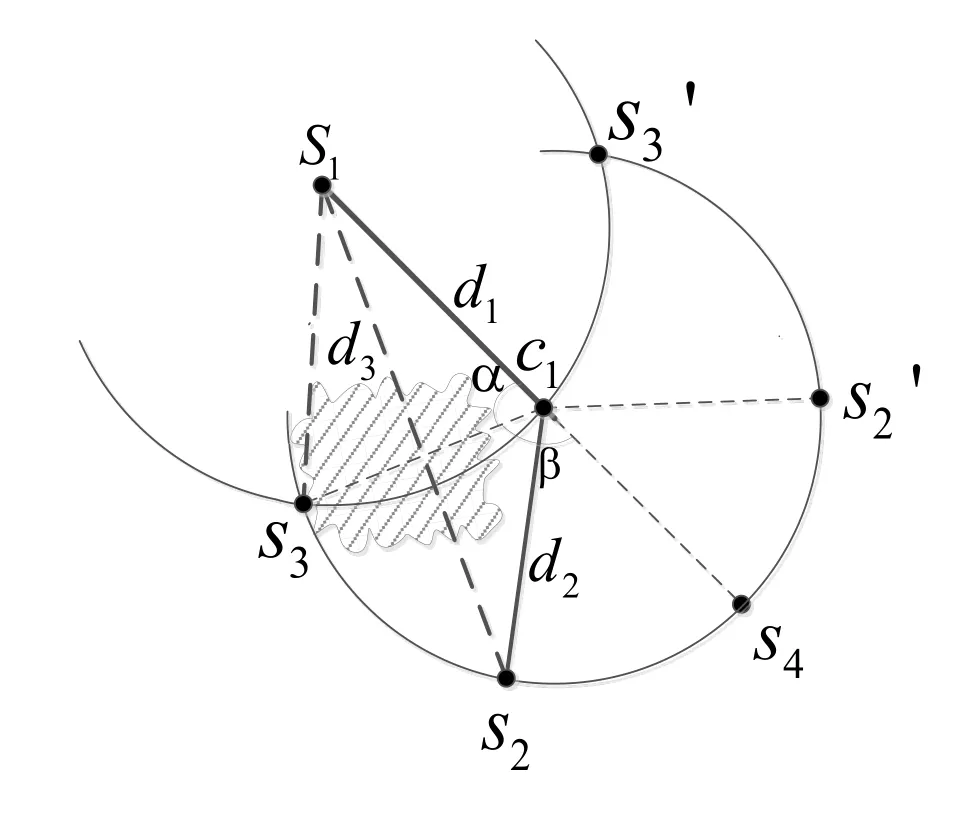
Figure 4: Heuristic connectivity compensation over energy hole

Assuming that s2lies on the middle of arc s3, s4, the equation can be expressed as:

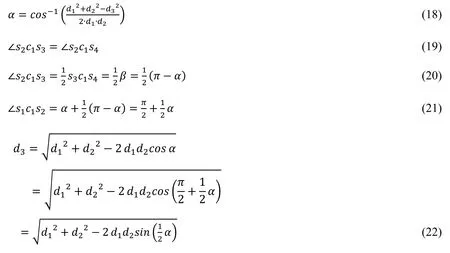
Therefore, d3is constructed and can be used as additional connectivity information on the border.The relaxed merging condition is met.

3.4 The complete MDS-MAP (CH) algorithm

This subsection presents the improved MDS-MAP (CH) localization algorithm for WSNs with energy holes by utilizing the schemes mentioned in previous subsetion 3.1～3.3 and the work flow of the new algorithm is shown in Fig.5.

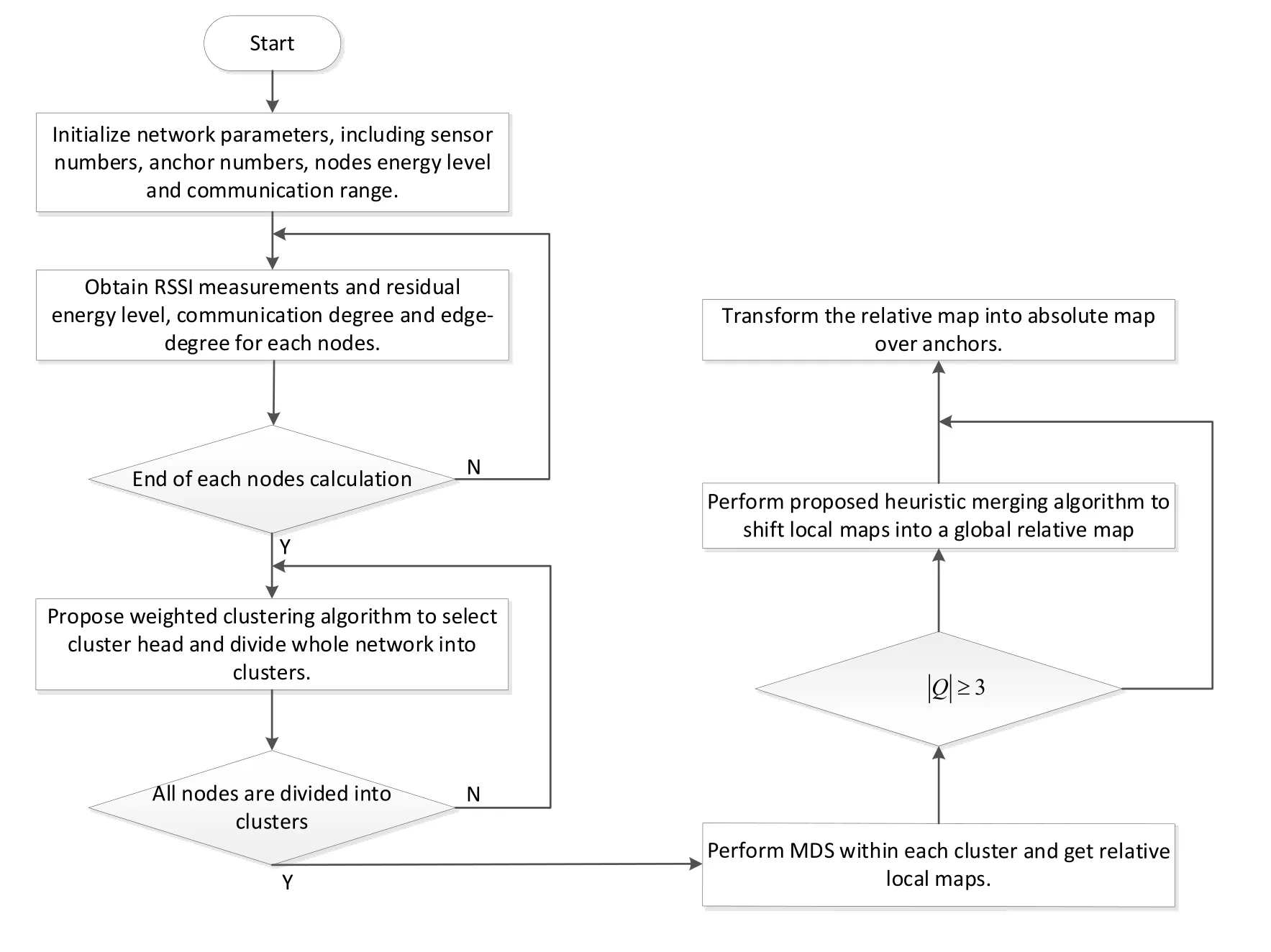
Figure 5: The flowchart of MDS-MAP (CH) algorithm

4 Experimental results and analysis

In order to evaluate the performance of MDS-MAP (CH) algorithm, we simulate a WSN system with Matlab and compare the performance of the proposed algorithm with the classical MDS-MAP algorithm and the improved MDS-MAP (P).The average estimation error E in the Eq.(21) is used as an index for evaluating the localization error of the algorithm.

where xest(i) denotes the estimated coordinates of the node i and xreal(i) represents the real coordinates of the node i, and R is the communication range.

4.1 Analysis of performance in uniform network

We first consider the performance of our algorithm in a uniformly deployed situation regarding error and energy consumption.We assume a sensor network randomly deployed on a square area and the anchor nodes are scattered randomly around the edges.Path loss is set to a fixed value.The influence of node density and residual energy is relatively lager than other factors.Therefore the order of weight factor should be φi＞Si＞edge(i).According to the weight calculation method of the centroid weights [Edwards, Stillwell and Seaver (1981)], the calculated weighted results are 0.61, 0.278, and 0.112.The node performance parameters are shown in Tab.1.

Table 1: Parameter dataset

We assume that there are 100 ordinary nodes randomly deployed on a 2-D plane and the average network connectivity is 10.There are four anchor nodes and the ranging error is 10%.Fig.6(a) shows the relative coordinates of nodes after all clusters are merged where the circles denote the ordinary nodes and the diamonds denotes the anchor nodes.Fig.6(b) displays the global absolute coordinates which were transformed from the map in Fig.6(a) by rotation and translation with the aids of anchor nodes.Fig.6(c) is a comparison between the estimated position (denoted by circles) calculated by the MDS-MAP (CH) algorithm, and the actual position (denoted by an asterisk).The average estimation error is around 30% in this case, which can be reduced with the increase of connectivity and the number of anchor nodes and simulation results are illustrated later.

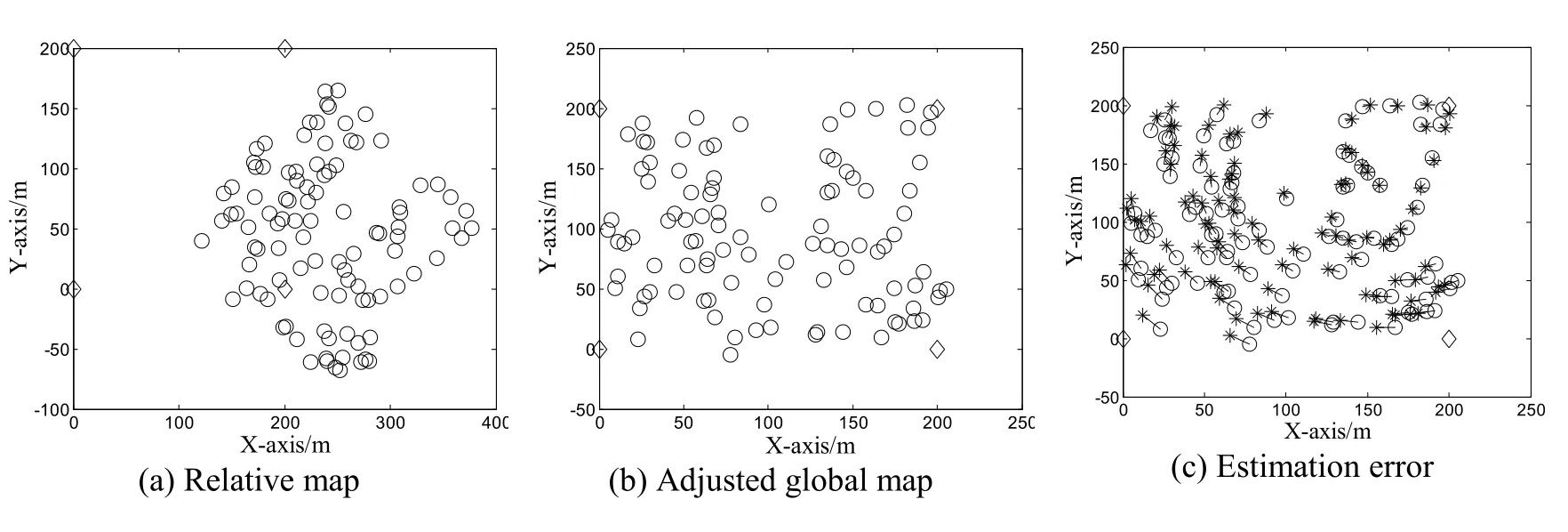
Figure 6: Localization estimation in a uniformly distributed network

The performance regarding energy consumption in large-scale networks of the proposed method is compared with the classical MDS-MAP algorithm.As shown in Fig.7, after over 100 trails for both algorithms, the new method is significantly superior to the MDS-MAP algorithm in terms of energy consumption and residual energy, and the energy level can be maintained at a high level within the first two hundred runs.Simulation result shows that when the density goes higher, the energy decays faster.However, the proposed method maintains a stable energy decay speed as the residual energy level goes lower.

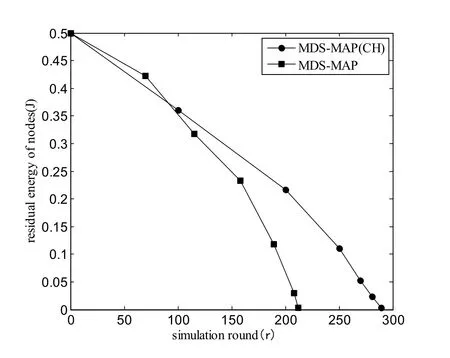
Figure 7: Comparison of algorithms in average residual energy level

4.2 Effect of anchor percentage

We assume that the percentage of anchor nodes are 4%, 6%, 10% and 20% respectively in Figs.8(a)-8(d), and the average connectivity are adjusted by changing the transmission ranges.The degrees of connectivity are adjusted from 7 to 30 and the growth step is 3.Comparison of the classical MDS-MAP algorithm, the improved MDS-MAP (P) algorithm and the proposed MDS-MAP (CH) algorithm are conducted regarding to average estimation error after 50 simulations.When the degree of connectivity is less than 8, the proposed MDS-MAP (CH) algorithm significantly outperforms others.With the increase of connectivity degree, the average estimation error of all the algorithms decreases.As shown in Fig.8.The performance of the other two algorithms can catch up by the increasing the degree of connectivity, but at the cost of introducing redundancy and consuming more energy.

With the increase of the number of anchor nodes, as shown in Fig.8(a) to Fig.8(d), the localization accuracy of the algorithm goes higher.The average estimation error of the MDS-MAP (CH) algorithm proposed in this paper under each degree of connectivity is smaller than the other two algorithms and the localization results are better.

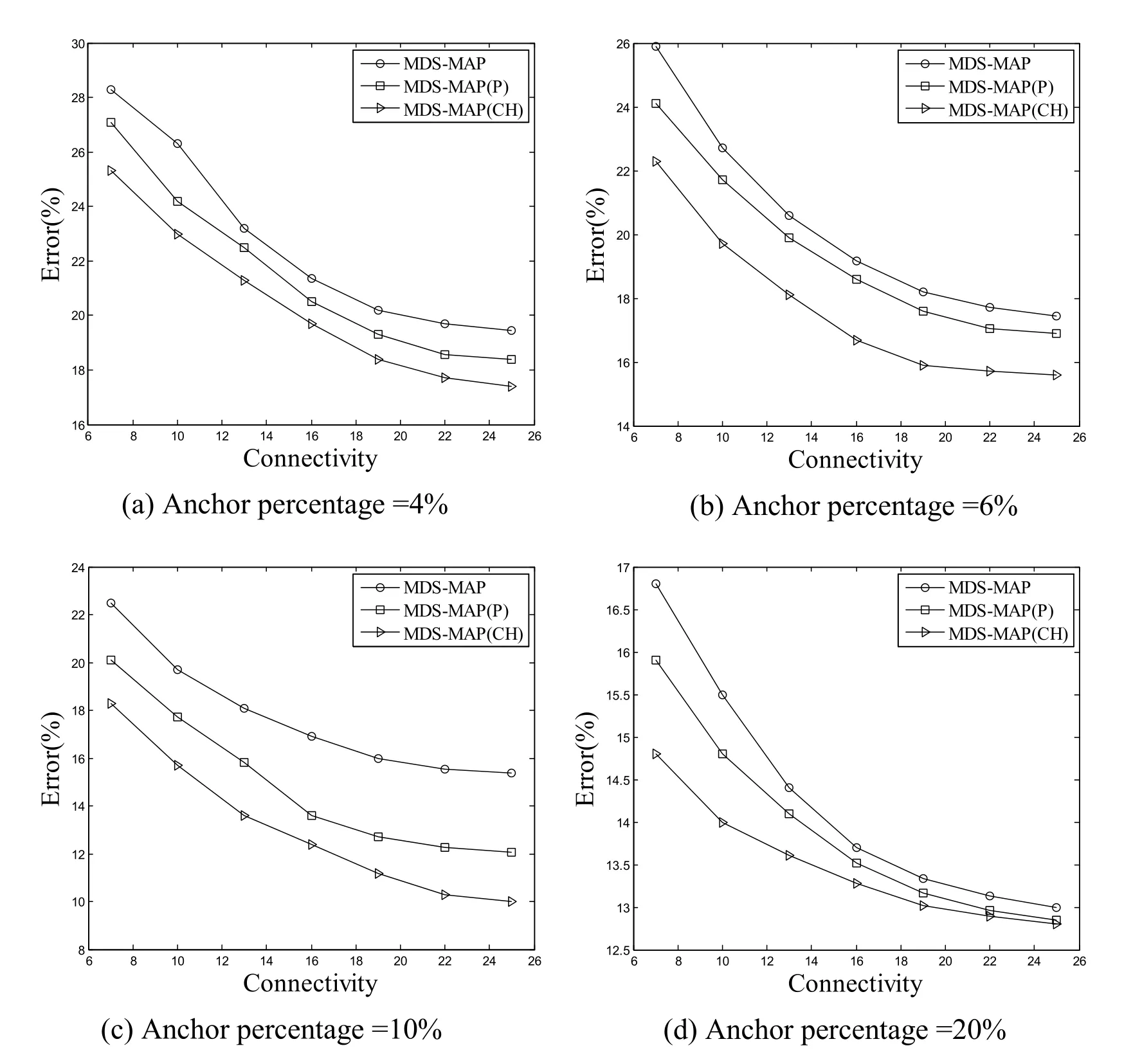
Figure 8: Performance comparison under different anchor percentage

4.3 Effect of different network patterns

In this subsection, the effect of two typical anisotropic network patterns where our MDSMAP (CH) algorithm is applied are studied.When calculating the virtual connectivity over the energy holes, two patterns are analyzed here: O-shape in Figs.9(a)-9(b) and Hshape in Figs.9(c)-9(d).Hop density is assumed to be 10/100 m2, the anchor percentage is 20%.We can see the performance in terms of error in Fig.9, where the estimated position (denoted by circles) calculated by localization algorithm and the actual position (denoted by an asterisk), that compared with MDS-MAP (P) the MDS-MAP (CH) localization result is more accurate.Evaluating the performance with Eq.(23) and the error can be improved by 30-40% compared to MDS-MAP (P).

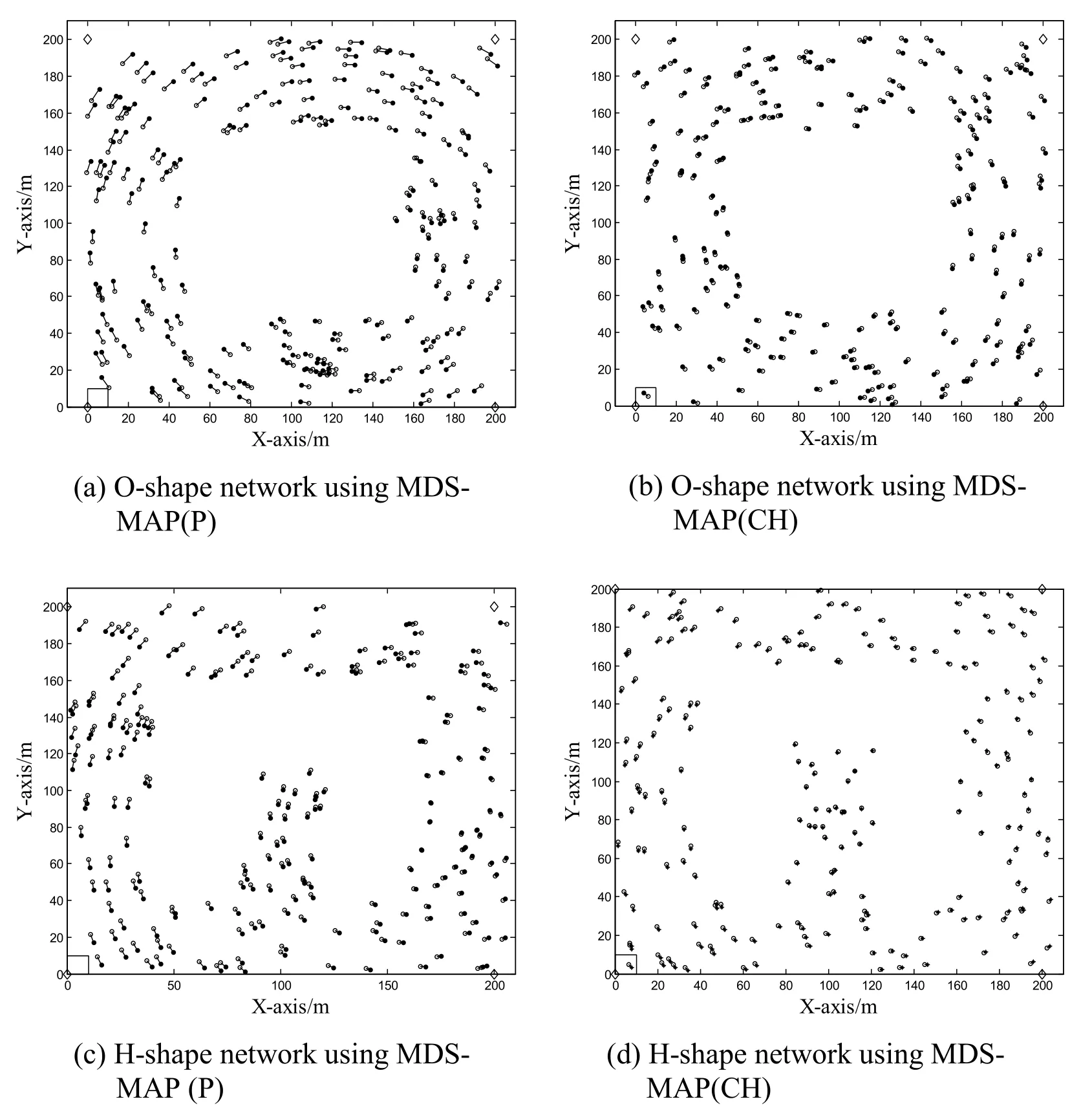
Figure 9: Comparison of error using our algorithm and MDS-MAP (P)

5 Conclusions and future work

In this paper, we proposed a MDS-MAP (CH) localization algorithm that aims at balancing energy consumption, reducing communication costs and lowering merging demand for an anisotropic network with energy holes.Because the cluster heads determine the performance of the algorithm, the authors proposed a weight-based clustering scheme.In this clustering scheme, with graph topology feature and energy load regarded as weighting factors, which can be adjusted flexibly according to realistic systems.The heuristic method is used to estimate missing distance information and compensate common nodes set to thus improve the merging rule.Experimental results show that the MDS-MAP (CH) algorithm performs better than the existing algorithms in higher accuracy and lower energy overhead, and suits well in practical large-scale network scenarios.In the future, a lot of our effort will be focusing on further increasing the accuracy of the heuristic merging method and a more dynamic weighted clustering strategy when considering energy level and topology vary at different time.

Acknowledgement:This research was financially supported by Nanjing Tech University, Introduction Talent Start-up Fund (Grant No.39809110).

References

Arumugam, G.S.; Ponnuchamy, T.(2015): EE-LEACH: development of energyefficient LEACH Protocol for data gathering in WSN.EURASIP Journal on Wireless Communications and Networking, pp.1-9.

Anchao, L.I.; Guifen, C.(2017): An improved clustering routing algorithm for energy heterogeneous wireless sensor networks.Chinese Journal of Sensors and Actuators, vol.6, no.11, pp.1712-1718.

Adissi, M.; Lima, F.A.; Gomes, R.D.; Silva, D.B; Belo, F.(2017): Implementation and deployment of an intelligent industrial wireless system for induction motor monitoring.Journal of Dynamic Systems, Measurement, and Control, vol.139, no.12, 124502-124502-8.

Biljana, S.; Danco, D.; Andrea, K.(2008): Cluster-based MDS algorithm for nodes localization in wireless sensor networks with irregular topologies.Proceedings of the 5th International Conference on Soft Computing as Transdisciplinary Science and Technology, pp.384-389.

Cheng, L.; Qian, D.; Wu, W.(2008): An energy efficient weight-clustering algorithm in wireless sensor networks.Japan-China Joint Workshop on Frontier of Computer Science and Technology, pp.30-35.

Carmelo, D.F.; Mauro, M.; Enrico, B.; Enrico, B.; Giorgio, C.(2018): Dynamic Multidimensional Scaling with anchors and height constraints for indoor localization of mobile nodes.Robotics and Autonomous Systems, vol.108, no.3, pp.28-37.

Edwards, D.A.; Stillwell, W.G.; Seaver, D.A.(1981): A comparison of weight approximation techniques in multi attribute utility decision making.Organizational Behavior and Human Performance, vol.28, no.1, pp.62-77.

Fang, X.; Jiang, Z.; Nan, L.(2016): Noise-aware localization algorithms for wireless sensor networks based on multidimensional scaling and adaptive Kalman filtering.Computer Communications, vol.101, no.5, pp.57-68.

Hightower, G.B.J.(2001): Locations systems for ubiquitous computing.IEEE Computer, vol.34, no.6, pp.57-66.

Jia, D.; Li, W.; Wang, P.; Feng, X.; Li, H.; Jiao, Z.(2016): An advanced distributed MDS-MAP localization algorithm with improved merging strategy.IEEE International Conference on Information and Automation, pp.1980-1985.

Kim, E.; Woo, S.; Kim, C.(2007): LaMSM: localization algorithm with merging segmented maps for un-derwater sensor networks.Emerging Directions in Embedded and Ubiquitous Computing, Euc Workshops: Trust, Wsoc, Ncus, Uuwsn, Usn, Eso, and Secubiq, pp.445-454.

Minhan, S.; Minho, J.; Hyunseung, C.(2012): An interactive cluster-based MDS localization scheme for multimedia information in wireless sensor networks.Computer Communications, vol.35, no.15, pp.1921-1929.

Perumal, P.S.; Utharaj, V.R.; Christo, V.R.E.(2014): Intelligent UAV-assisted localisation to conserve battery energy in military sensor networks.Defence Science Journal, vol.64, no.6, pp.557-563.

Sundararajan, V.; Redfern, A.; Schneider, M.; Wright, P.; Evans, J.(2005): Wireless sensor networks for machinery monitoring.ASME 2005 International Mechanical Engineering Congress and Exposition, pp.425-433.

Sahu, P.K.; Wu, E.H.; Sahoo, J.(2013): Dual RSSI trend based localization for wireless sensor networks.IEEE Sensors Journal, vol.13, no.8, pp.3115-3123.

Shang, Y.; Ruml, W.(2004): Improved MDS-based localization.Joint Conference of the IEEE Computer and Communications Societies, Hong Kong, pp.2640-2651.

Shi, Z.; Meng, J.E.; Zhang, B.H.; Naderahmadian, Y.(2017): A novel heuristic algorithm for node localization in anisotropic wireless sensor networks with holes.Signal Processing, vol.138, no.3, pp.27-34.

Saeed, N.; Nam, H.(2016): Cluster based multidimensional scaling for irregular cognitive radio networks localization.IEEE Transactions on Signal Processing, vol.64, no.10, pp.2649-2659.

Tashnim, J.S.; Chowdhury, C.E.; Vijay, D.; Danda, B.R.; Jared, O.(2016): Advances on localization techniques for wireless sensor networks: a survey.Computer Networks, vol.11, no.22, pp.284-305.

Yu, X.W.; Zhou, L.X.; Zhang, F.(2017): Self-localization algorithm for deep mine Wireless Sensor Networks based on MDS and rigid subset.2017 IEEE 2nd International Conference on OPTO-Electronic Information Processing, pp.6-10.