李紅春,夏梅珍

(1.揚州大學(xué)信息工程學(xué)院,江蘇 揚州 225127;2.揚州工業(yè)職業(yè)技術(shù)學(xué)院電氣與信息工程學(xué)院,江蘇 揚州 225127)

1 問題描述及基本假設(shè)

考慮一類具有死區(qū)輸入的未建模動態(tài)系統(tǒng)

(1)

其中Xi=[x1…xi]T(i=1,…,n)是系統(tǒng)可測狀態(tài),z∈Rn0是未建模動態(tài)項,q(z,Xn,t)是符合Lipschit條件的函數(shù),hi(Xi,xi+1)是未知光滑函數(shù),Δi(z,Xn,t)是動態(tài)擾動,f(Xn)和g(Xn)是未知光滑函數(shù),D(t)是非線性死區(qū)模型輸入u(t)的輸出,y是系統(tǒng)輸出,d+和d-為未知正常數(shù),dr(u(t))和dl(u(t))為區(qū)間內(nèi)的實際映射,均為平滑的未知連續(xù)函數(shù)．控制目標(biāo)是構(gòu)造控制律u(t),使系統(tǒng)(1)的輸出y在死區(qū)輸入等因素影響下自適應(yīng)地跟蹤給定輸入yr,并確保閉環(huán)系統(tǒng)半全局一致最終有界,且|y|≤kc1(?t≥0)成立,kc1是正常數(shù)．

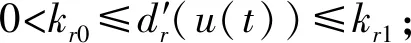
根據(jù)假設(shè)1,死區(qū)模型可寫為D(t)=H(u)u(t)+d(u(t)),其中

且min{kr0,kl0}≤H(u)≤min{kr1,kl1}=K,|d(u)|≤d*,d*=max{kr1,kl1}max{d+,d-}是未知常數(shù)．

假設(shè)3增益g(Xn)符號未知,且滿足0<|g(Xn)|≤gM,其中g(shù)M為未知正常數(shù)．

假設(shè)4存在均非負(fù)未知連續(xù)函數(shù)ρi1(·)和ρi2(·),且ρi2(·)為單調(diào)增,滿足|Δi(z,Xn,t)|≤ρi1(‖Xi‖)+ρi2(‖z‖),i=1,…,n．

假設(shè)5[7]當(dāng)指數(shù)輸入狀態(tài)z=q(z,Xn)漸近穩(wěn)定時,有Lyapunov函數(shù)Q(z)使得α1(‖z‖2)≤Q(z)≤α2(‖z‖2),q(z,Xn)?Q(z)/?t≤-cQ(z)+γ(|x1|)+d,其中α1(·),α2(·)為K∞類函數(shù);γ(·)為已知K∞類函數(shù);c,d均為已知正常數(shù)．

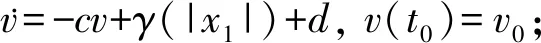
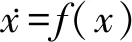
2 動態(tài)面控制器的設(shè)計

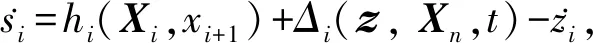
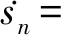
3 穩(wěn)定性分析

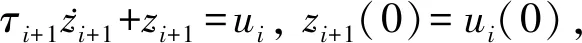
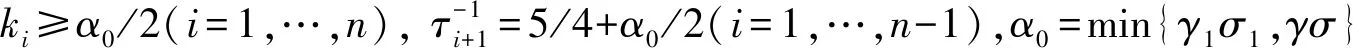
4 仿真算例

非線性系統(tǒng)

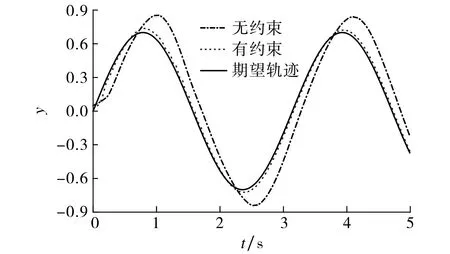
圖1 不同情況下輸出y與期望軌跡Fig.1 Output y and desired trajectory under two cases

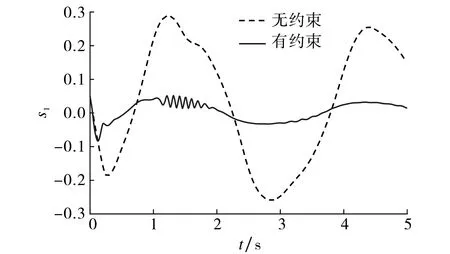
圖2 不同情況下的跟蹤誤差s1Fig.2 Tracking error s1 under two cases