FORCED OSCILLATION OF FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS WITH DAMPING TERM
MA Qing-xia,LIU Ke-ying,LIU An-ping
(1.School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China)
(2.School of Mathematics and Information Sciences,North China University of Water Resources and Electric Power,Zhengzhou 450045,China)
Abstract:In this paper,we study the forced oscillation of a fractional partial differential equation with damping term subject to Robin boundary condition.Using an integration average technique and the properties of the Riemann-Liouville calculus,we obtain some new oscillation criteria for the fractional partial differential equations,which are the generalization of some classical results involving partial differential equations.Two examples are given to show the applications of our main results.
Keywords: fractional partial differential equations;forced oscillation;Riemann-Liouville fractional calculus
1 Introduction
Fractional differential equations(FDE)played an important role in the modeling of many phenomena in various fields such as viscoelasticity,electroanalytical chemistry,control theory,many physics problems,etc.In the past few years,many articles investigated some aspects of fractional differential equations,such as the existence,the uniqueness and stability of solutions,the methods for explicit and numerical solutions,see for example,the books[1–5].Recently,the research on oscillation of various fractional differential equations was a hot topic,see[6–9].However,to author’s knowledge,very little is known regarding the oscillatory behavior of fractional partial differential equations up to now,see[10–14].In[13],by using the generalized Riccati transformation and the properties of fractional calculus,the author considered the forced oscillation of a fractional partial differential equation of the form

with two boundary conditions
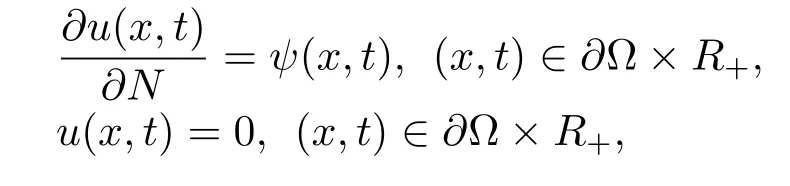
whereR+=[0,∞),α∈(0,1)is a constant,is the Riemann-Liouville fractional derivative of orderαwith respect totof a functionu(x,t).
In this paper,we use only the properties of fractional calculus without the generalized Riccati transformation to consider the forced oscillation of the fractional partial differential equation with damping term of this form
with the boundary condition
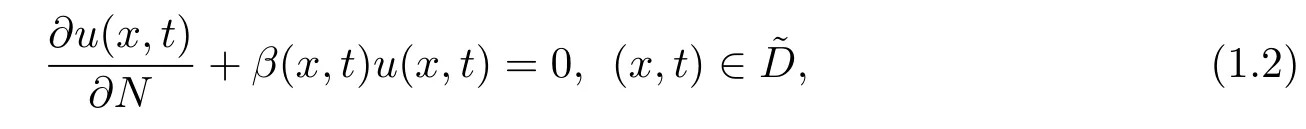
where ? is a bounded domain inRnwith a piecewise smooth boundary??,?is the Laplacian inRn,Nis a unit exterior normal vector to??,β(x,t)is a continuous nonnegative function on;α ∈(0,1)is a constant,(x,t)is the forced term of the equation.

We assume throughout this paper that
A1)r(t)∈C1(R+,R+),a(t)∈C(R+,R+),p(t)∈C(R+,R);
A3)f(u)∈C(R,R)for all,kis a positive constant.
Definition 1.1By a solution of problem(1.1)–(1.2),we mean a functionu(x,t)which satisfies(1.1)and the boundary condition(1.2).
Definition 1.2A solution of problem(1.1)–(1.2)is said to be oscillatory inDif it is neither eventually positive nor eventually negative.Otherwise it is called nonoscillatory.
2 Preliminaries
In this section,we introduce the definitions and properties of fractional integrals and derivatives,which are useful throughout this paper.There are several kinds of definitions of fractional integrals and derivatives[2].In this paper,we use Riemann-Liouville definition.
Definition 2.1The Riemann-Liouville fractional partial derivative of orderα∈(0,1)with respect totof a functionu(x,t)is defined by

provided the right hand side is pointwise defined onR+,where Γ(z)is the Gamma function defined by

forz>0.
Definition 2.2The Riemann-Liouville fractional integral of orderα∈R+of a functiony(t)is defined by
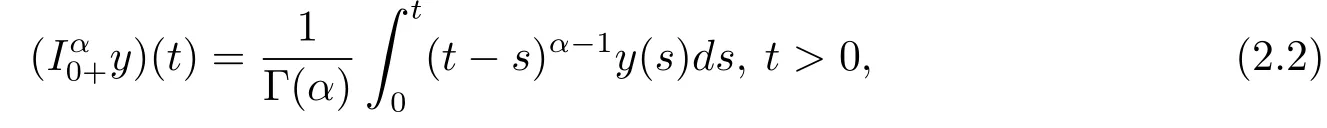
provided the right hand side is pointwise defined onR+.
Definition 2.3The Riemann-Liouville fractional derivative of orderα∈R+of a functiony(t)is defined by
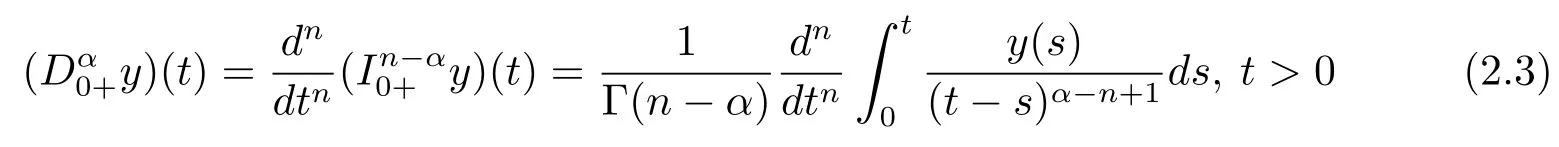
withn=[α]+1,where[α]means the integer part ofα.
Lemma 2.4Letα>0,m∈N andD=d/dx.If the fractional derivativesandexist,then

Lemma 2.5Let

then

3 Main Results
For convenience,we introduce the following notations
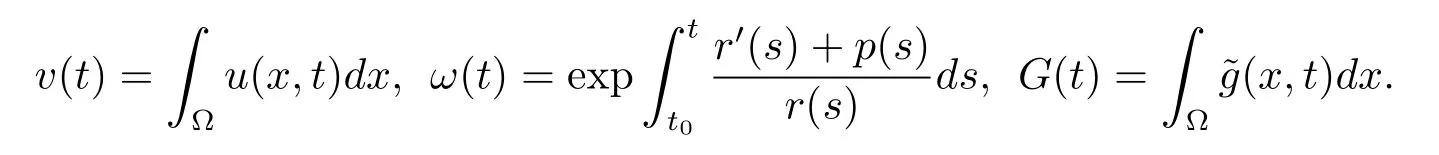
Lemma 3.1Ifu(x,t)is a positive solution of problems(1.1)–(1.2)in the domainD,thenv(t)satisfies the fractional differential inequality
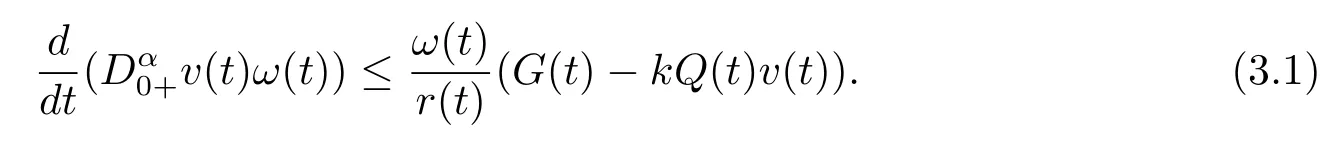
ProofLetu(x,t)is a positive solution of problem(1.1)–(1.2)in the domainD,then there existst0>0,such thatu(x,t)>0 in ?×[t0,∞).Integrating(1.1)with respect toxover ? yields

From A2)and A3),it is easy to see that
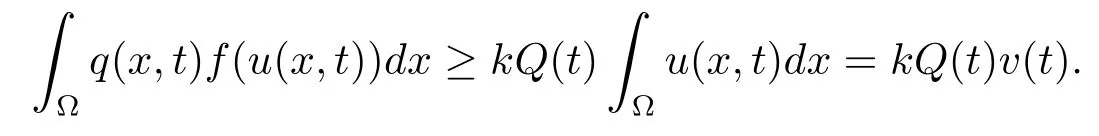
Green’s formula and the boundary condition(1.2)yield
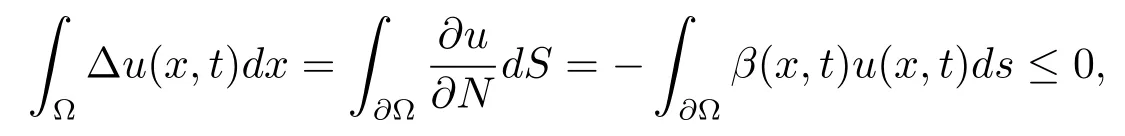
wheredSis the surface element on??.It shows thatv(t)satisfies the inequality
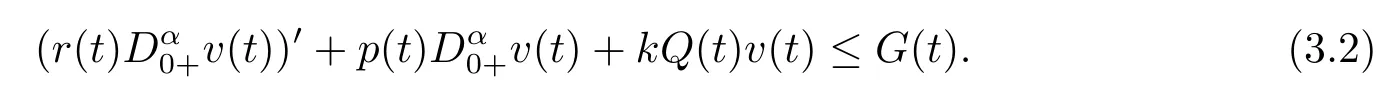
Using Lemma 2.4 and inequality(3.2),we obtain

which shows thatv(t)is a positive solution of inequality(3.1).The proof is completed.
Lemma 3.2Ifu(x,t)is a negative solution of problems(1.1)–(1.2)in the domainD,
thenv(t)satisfies the fractional differential inequality

ProofLetu(x,t)is a negative solution of problems(1.1)–(1.2)in the domainD,then there exists,such that.Integrating(1.1)with respect toxover ? yields
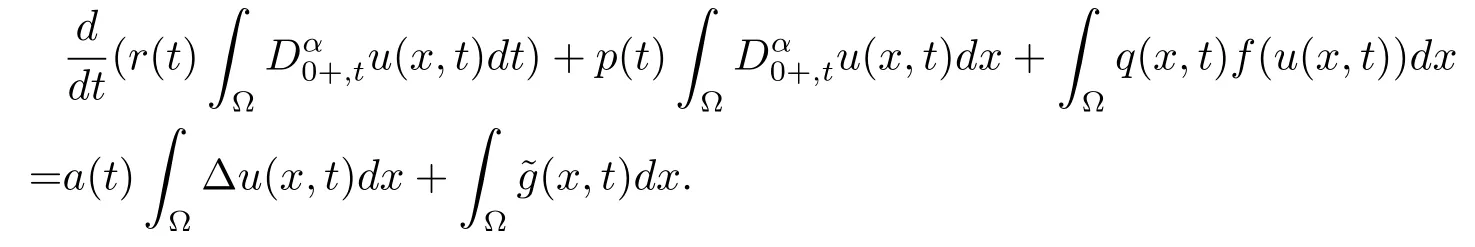
From A2)and A3),it is easy to see that
Green’s formula and the boundary condition(1.2)yield
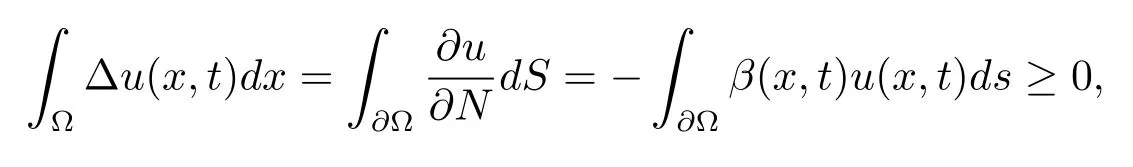
wheredSis the surface element on??.It shows thatv(t)satisfies the inequality

Using Lemma 2.4 and inequality(3.4),we obtain

which shows thatv(t)is negative solution of inequality(3.3).The proof is completed.
Theorem 3.3If inequality(3.1)has no eventually positive solutions and the inequality(3.3)has no eventually negative solutions,then every solution of problems(1.1)–(1.2)is oscillatory inD.
ProofSuppose to the contrary that there is a nonoscillatory solutionu(x,t)of problems(1.1)–(1.2).It is obvious that there exists0such thatu(x,t)>0 oru(x,t)<0 fort≥0.
Ifu(x,t)>0,t≥0,by using Lemma 3.1,we obtain thatv(t)>0 is a solution of inequality(3.1),which is a contradiction.
Ifu(x,t)<0,t≥0,by using Lemma 3.2,we obtain thatv(t)<0 is a solution of inequality(3.3),which is a contradiction.The proof is completed.
Lemma 3.4If
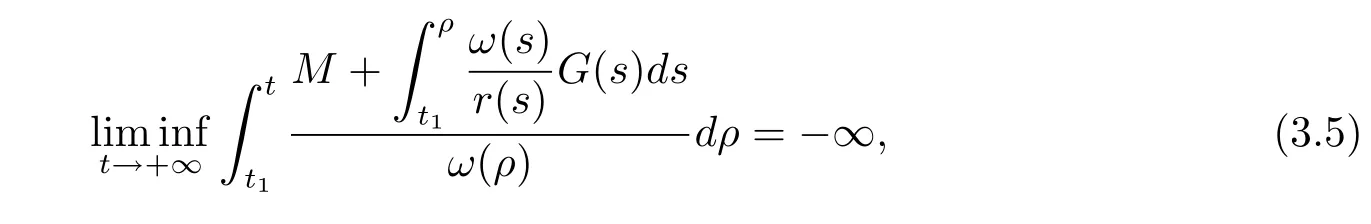
then inequality(3.1)has no eventually positive solutions.
ProofSuppose to the contrary that(3.1)has a positive solutionv(t),then there existst1≥t0such thatv(t)>0,t≥t1.Integrating both sides of(3.1)fromt1tot,we obtain
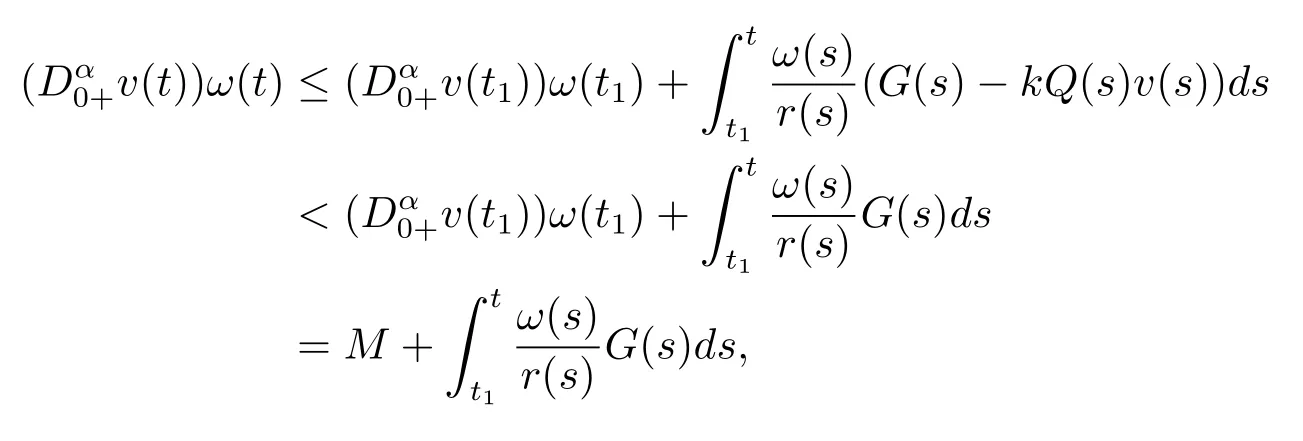
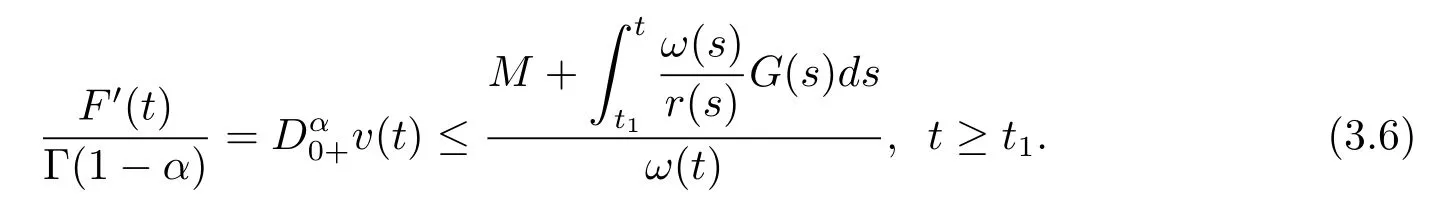
Integrating(3.6)fromt1tot,we obtain

Takingt→∞,from(3.7),we have
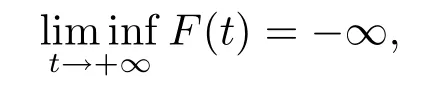
which contradicts the conclusion thatv(t)>0.The proof is completed.
Lemma 3.5If

then inequality(3.3)has no eventually negative solutions.
Using Theorem 3.3,Lemma 3.4 and Lemma 3.5,we immediately obtain the following theorem.
Theorem 3.6If(3.5)and(3.8)hold,then every solution of problems(1.1)–(1.2)is oscillatory inD.
4 Example
Example 4.1Consider the fractional partial differential equation

with the boundary condition
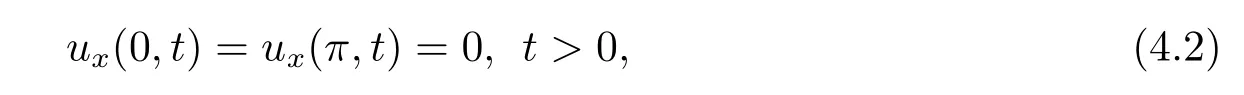
here


Hence
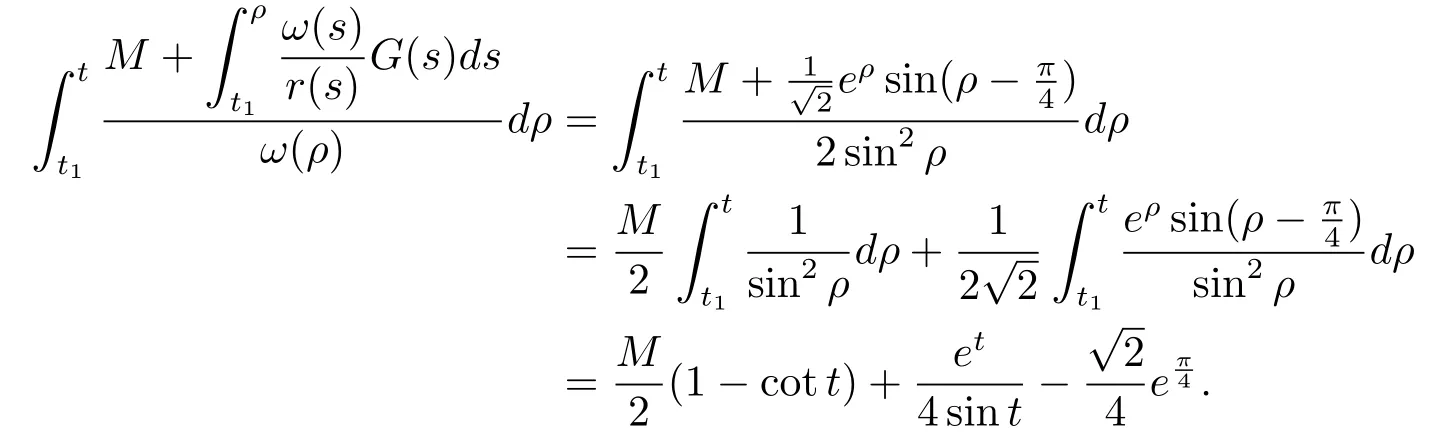
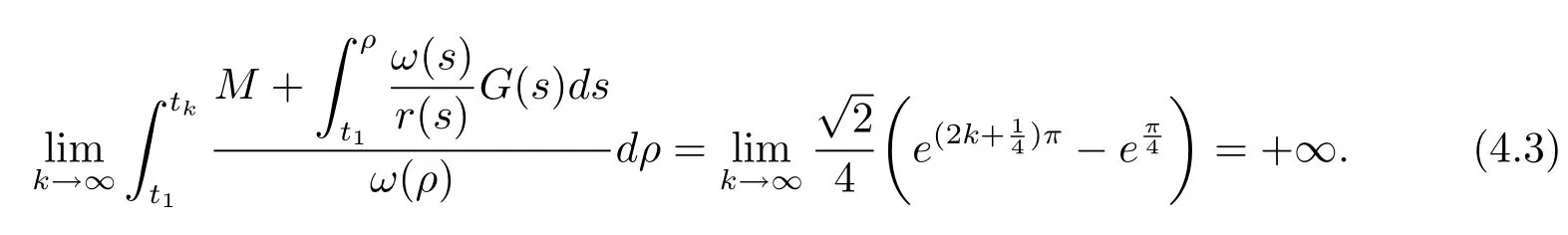

From(4.3),(4.4),we have

which shows that all the conditions of Theorem 3.6 are fulfilled.Then every solution of problems(4.1)–(4.2)is oscillatory in(0,π)×R+.
Example 4.2Consider the fractional partial differential equation

with the boundary condition(4.2),where

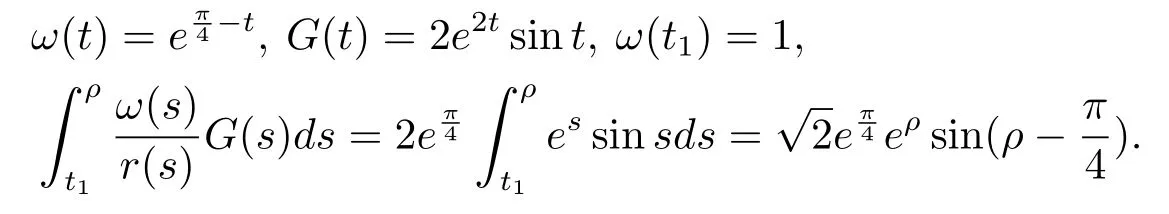
Hence
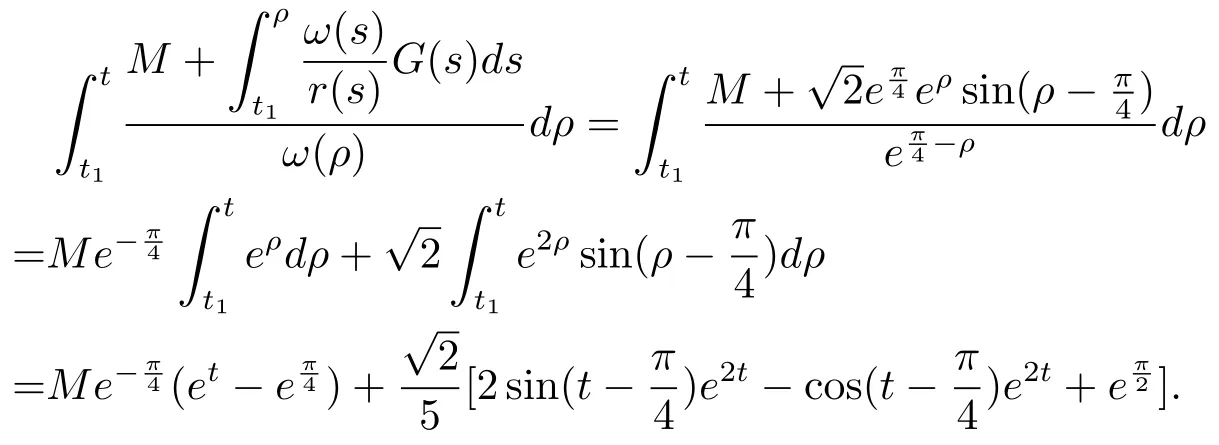

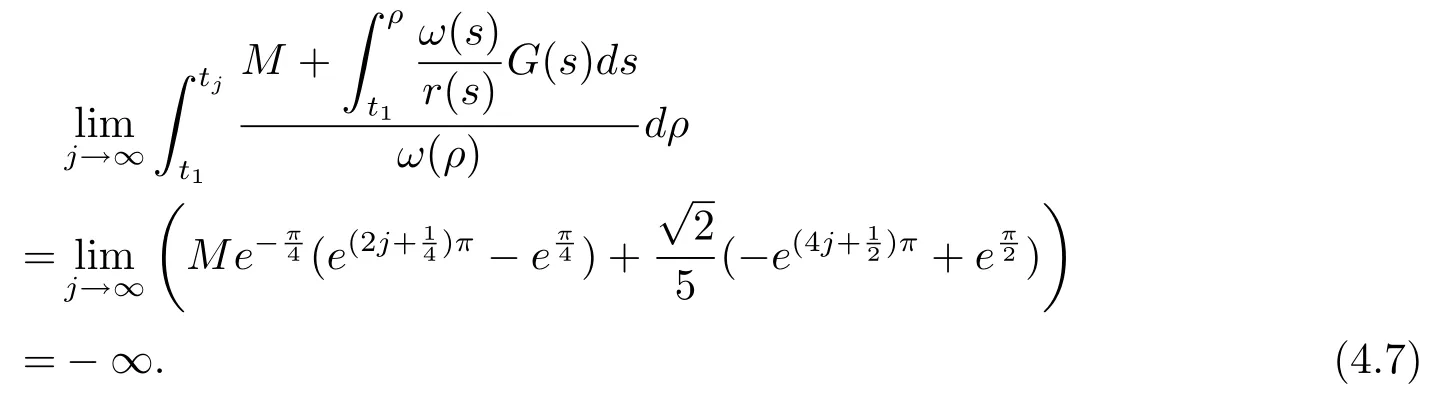
From(4.6),(4.7),we have
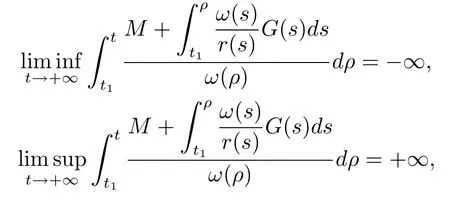
which shows that all the conditions of Theorem 3.6 are fulfilled.Then every solution of problem(4.5)with(4.2)is oscillatory in(0,π)×R+.
RemarkIn this paper,we did not mention oscillation of fractional partial differential equation with time delay.Actually,we have considered the following equation

with the boundary condition(1.2),whereτ,δare nonnegative constants and conditions A1)–A3)are satisfied.The conclusion is that if(3.5)and(3.8)hold,then every solution of problem(4.8)with(1.2)is oscillatory inD.That means time delaysτandδhave no effect on oscillatory property.
However,we have not studied the fractional partial differential equations with time delays which are on,since it is more complicated than discussion in this paper.In the future,we would like to discuss this case and hope to acquire desired results.

