Variable structure control for descriptor Markovian jump systems subject to partially unknown transition probabilities
Zhuang Huixuan Sun Qinglin Chen Zengqiang
(College of Artificial Intelligence, Nankai University, Tianjin 300350, China)(Key Laboratory of Intelligent Robots, Nankai University, Tianjin 300350, China)
Abstract:The descriptor Markovian jump systems (DMJSs) with partially unknown transition probabilities (PUTPs) are studied by means of variable structure control. First, by virtue of the strictly linear matrix inequality (LMI) technique, a sufficient condition is presented, under which the DMJSs subject to PUTPs are stochastically admissible. Secondly, a novel sliding surface function based on the system state and input is constructed for DMJSs subject to PUTPs; and a dynamic sliding mode controller is synthesized, which guarantees that state trajectories will reach the pre-specified sliding surface in finite time despite uncertainties and disturbances. The results indicate that by checking the feasibility of a series of LMIs, the stochastic admissibility of the overall closed loop system is determined. Finally, the validity of the theoretical results is illustrated with the example of the direct-current motor. Furthermore, compared with the existing literature, the state convergence rate, buffeting reduction and overshoot reduction are obviously optimized.
Key words:descriptor Markovian jump systems (DMJSs); variable structure control (VSC); partially unknown transition probabilities (PUTPs); stochastic admissibility
Descriptor systems,which are also known as singular systems, implicit systems, semi-state systems, differential algebraic systems, generalized state space systems, have been extensively studied over the past decades due to the fact that they can describe a great many natural phenomena compared to standard state-space systems[1-3]. Zhang et al.[4]explored the stability and stabilization of descriptor systems. More recently, Gao et al.[5]proposed stability criteria for descriptor Markovian jump systems (DMJSs) with fully known transition probabilities. However, variable structure control (VSC) for DMJSs subject to partially unknown transition probabilities (PUTPs) has been seldom investigated thoroughly[6-8].
VSC also refers to sliding mode control (SMC), which is an efficient robust control method to deal with uncertain systems, delay time systems and nonlinear systems. Due to its insensitive features to the variation of system parameters and external disturbance during the sliding phase, it has been extensively applied to a variety of practical engineering systems[9]. Utilizing a discontinuous control to drive the state trajectory to the pre-specified sliding surface and remain there for all subsequent time is the essence of VSC[10]. Over the past few decades, VSC has successfully been applied to problems such as automatic flight control, control of electric motors, chemical processes, helicopter stability augmentation systems, space systems and robots[11]. Recently, VSC has also been investigated in stochastic systems[12-15], time-delay systems[16-18]and MJSs[19-22]. However, only a little literature focuses on the VSC of DMJSs[1,22]. Li et al.[10]investigated the VSC problems for continuous-time DMJSs with a mode dependent derivative term coefficient. As far as we know, VSC for DMJSs subject to PUTPs has not been researched thoroughly. It must be mentioned that the entire information on transition probabilities is known, which is a common hypothesis for simplifying the analysis and synthesis of DMJSs in most of the studies. However, in practice, getting access to available transition probabilities sometimes seems unlikely, and the expenditure is possibly exorbitant or time-consuming. Hence, instead of having great complexity when surveying and estimating all the transition probabilities, it is necessary and important to further investigate more general DMJSs subject to PUTPs.
Motivated by the aforementioned facts, the dynamic sliding mode controller design problem for continuous-time DMJSs with PUTPs is studied. First, a sufficient condition, which guarantees that the DMJSs subject to PUTPS are stochastically admissible, is derived in the light of precise LMIs. Then, we construct a novel and high-performance sliding surface function for DMJSs subject to PUTPS and design an expeditious sliding mode controller to study the pre-specified sliding surface in finite time. The sliding surface function has two parameters which can be adjusted according to actual demand. The sliding mode controller is efficient and agile, which can drive systems’ steady operations. A standard is proposed to ensure the stochastic admissibility of the sliding mode dynamics according to the result of stochastic admissibility. Finally, the effectiveness and practicability of the acquired results are illustrated by a practical example.
1 Problem Formulation and Preliminaries
Fix the probability space (Ω,F,P) and consider the following DMJSs:
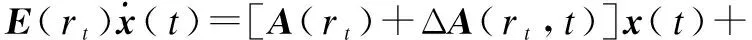
(1)
wherex(t)∈Rn,u(t)∈Rmare the state vector and input vector, respectively. {rt,t≥0} is the continuous-time discrete-state Markovian process taking values in l={1,2,…,N}. ΔA(rt,t)∈Rn×nis the uncertain matrix, andw(t)∈Rlis the disturbance. The switching behavior between different modes is described by the following transition probabilities:
(2)
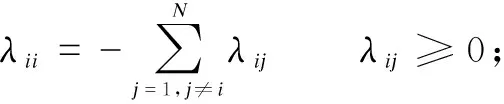
(3)
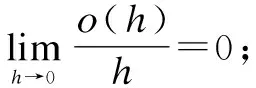
ΔAi(t)=DiHi(t)Vi
(4)
Thus, we can rewrite the linear singular system as
(5)
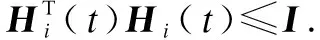
(6)
Furthermore, the transition probabilities of the jumping process in this paper are considered to be partially unavailable, that is, some elements in matrixΛis unknown. For example, for system (6) withNoperation modes, the Markovian process transition probabilities matrixΛcan be defined as
(7)
where * represents the unavailable elements. For convenience, ?i∈l, l=lik+liukis denoted as
lik={j:λijis known}, liuk={j:λijis unknown}
(8)
Then, if lik≠?, it is further depicted as
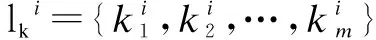
(9)
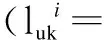
In this paper, our aim is to develop a sufficient condition such that the unforced continuous-time DMJSs (6) with PUTPs (8) is stochastically admissible and to design a sliding mode controller for system (6) with PUTPs (8) such that the resulting closed-loop system is stochastically admissible.
Lemma1[23]LetX,Y,Fbe the real matrices of appropriate dimensions withFT(t)F(t)≤Ithen
XFY+YTFTXT≤XXT+YTY
(10)

2 Main Results
In this section, the stability will be studied and the sliding mode controller will be designed based on Lemma 1 and the VSC theory, respectively.
2.1 Sliding mode function design
A novel sliding surface function is designed as follows:
(11)
Note that the sliding surface function of our design is a dynamic sliding surface.Bi∈Rm×m,Ei∈Rn×n,x(t)∈Rn, andGi∈Rm×ncan be regarded as an adjustable parameter matrix andβi∈Rn×nis a constant matrix which can be chosen arbitrarily.
Remark2Enlightened by the sliding surface function[9], dynamic VSC for the T-S fuzzy system is considered. We design a novel sliding surface function (11) on account of system states and inputs for DMJSs (6) with PUTPs (8). It is worth mentioning that the sliding surface function in Ref.[5] cannot be applied to the DMJSs (6) with PUTPs (8) directly. Hence, referring to Ref.[5], it is necessary to design a novel sliding surface function (11), which is suitable for the DMJSs (6) with PUTPs (8).
While the trajectories reach the sliding surface, we can deriveS(t)=0. Then, we can derive the derivation of the sliding surface as follows:
(12)
Substituting Eq.(6) into Eq.(12), we can derive
(13)
Letu(t)=ueq(t), and we can obtain the equivalent controlueq(t) as
(14)
Substituting the equivalent controlueq(t) into Eq.(6), we can obtain the equivalent dynamic system of the original system as
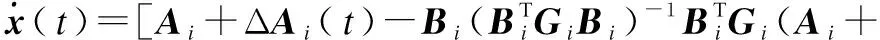
(15)
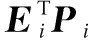
(16)
where
ProofThe following candidate of the Lyapunov function is chosen to analyze the stability of the equivalent dynamic system (15):
(17)
Then, taking the time derivative along the state trajectory of system (15), we obtain
xT(t){[Ai+ΔAi(t)-Bi(GiBi)-1Gi(Ai+
(18)
By using Lemma 1, the following inequality can be obtained:
(19)
Substituting inequality (19) into Eq.(18), it can be derived that
(20)
By applying Schur complement Lemma 2 to (20), it can be obtained that
(21)
which is equivalent to (16).
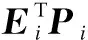
Remark3During the design of the novel nonlinear sliding surface function, the adjustable parameter matrixGiand adjustable constant matrixβiare introduced into the switching function; furthermore, these two adjustable variables are introduced into the LMI (16). The conservatism of the LMI condition can be decreased due to the existence of these two adjustable variables.
2.2 Dynamic sliding mode controller
The VSC problem for DMJSs (6) with PUTPs (8) will be investigated in this subsection. Next, the dynamic sliding mode controller will be designed, which can make the system state trajectory converge to the predefined sliding surface in finite time and thereafter remain on there.
In what follows, a dynamic sliding mode controller based on the system states and inputs will be designed, which assures the reachability of predefined sliding surface (14) in finite time. Thus, the following result can be obtained.
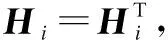
Φj-Hi≤0j∈liuk,j≠i
(22)
Φj-Hi≥0j∈liuk,j≠i
(23)
and the sliding mode controller is constructed by
βiEix(t)+ρsign(S(t))-
(24)
whereρis a positive constant which is adjustable, andζis a very small constant.
Then, the state trajectories of the DMJSs (6) subject to PUTPs (8) are converged to the sliding surfaceS(t)=0 in finite time and maintained there for all subsequent time.
ProofChoose the Lyapunov functional candidate as
(25)
Taking the weak infinitesimal generator ofV(x(t),i) and considering (13), we have
then
Bi(u(t)+Fiw(t))-Eiβix(t)]}TΦiS(t)+
(26)
Considering (24) and after collating (26), we can obtain
(27)
(28)
By adding the left side of (22) into (21), we obtain
Note that, the set of LMIs (22) and (23) are equivalent to the following inequality:
(29)
Hence, one can acquire
LV(x(t),i)<0
(30)
which yields that the state trajectories converge to the pre-specified sliding surface in finite time. The proof is completed.
3 Simulation and Result Analysis
In this section, we provide a practical example to testify the advancement and superiority of the proposed method.
We consider the DC motor[23], which represents the actuator that is usually encountered in the position control servo-mechanism. As shown in Fig.1, a load is driven by the DC motor. In Ref.[23], the author ignored the influence of the inductanceLi,i=1,2,3, while in this example, the inductance will be taken into consideration. The switch composed of three positions is also observed, and we hypothesize that the switches from one position to the other are dominated by a continuous-time Markovian chain {rt,t≥0} withrt∈l={1,2,3} as shown in (2). For eachrt=i∈l,RiandLiare adopted to represent the active resistances and the inductances, where the active resistance can be implemented by a differential amplifier. The voltage of the inductance, current, the voltage of the source and the speed of the shaft at timetare denoted byuL(t),i(t),u(t) andw(t), respectively. According to the electrical and mechanical law, we obtain
(31)
whereKwandKtare the electromotive force constant and the torque constant;JmandJcare the moments of inertia of the motor and load;bmandbcare the damping ratios of the motor and load, respectively;nis the gear ratio, and
(32)
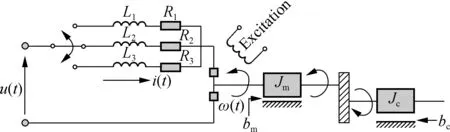
Fig.1 Block diagram of a DC motor
Additionally, letx1(t)=i(t),x2(t)=w(t), andx3(t)=uL(t). System (31) can be rearranged in the following form:
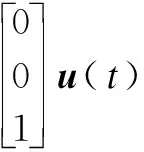
(33)
If we chooseKw=4,Kt=2.5,Jm=1,Jc=8,bm=1.5,bc=2,n=3,R1=5,R2=4,R3=3,L1=2,L2=3,L3=4, then, from (31) and (32), we can obtain Eq.(6) with the following parameters:
Hypothesize that the mismatched uncertainties in system (6) are depicted by
D1=(-0.5 0.5 0)T
V1=(-0.2 0.2 0),H1=sin(t)
D2=(0 0.5 -0.5)T
V2=(-0.2 0.2 0),H2=cos(t)
D3=(-0.5 0 0.5)T
V3=(-0.2 0.2 0),H3=sin(t)
The transition probabilities matrix is given by
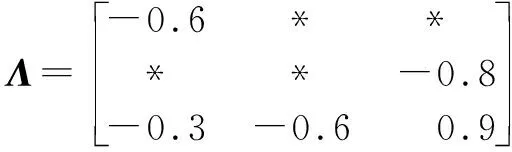
Now, solving LMIs (22) and (23) in Theorem 2 to design a sliding mode controller of the form (24) yields
Φ1=2.43,Φ2=1.76,Φ3=2.34
H1=1.38,H2=1.51,H3=1.68
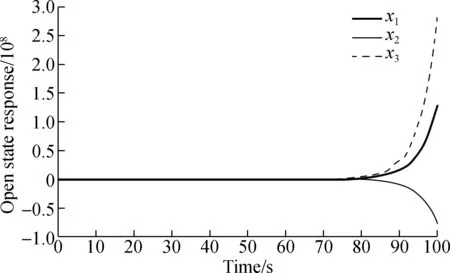
A feasible solution cannot be found by checking the conditions (15) for system (33), and according to Fig.2, system (33) cannot be stochastically admissible. As for the model shown in Fig.1, its performance can be damaged by instability or impulse or even destroyed. Thus, it is necessary to design a controller to guarantee that the resultant closed loop system is stochastically admissible.
(a)
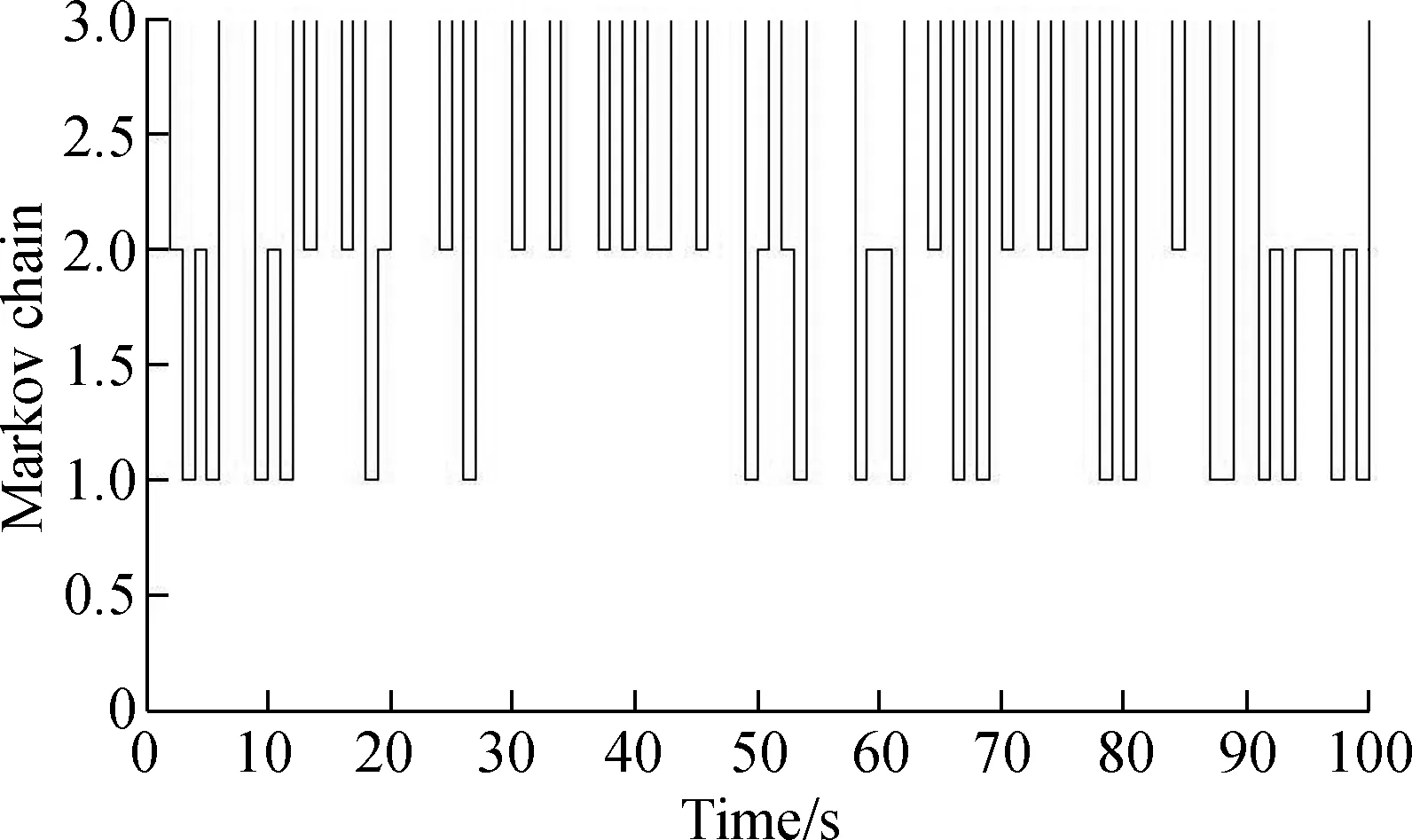
(b)Fig.2 State responses. (a) Open loop system;(b) Markov chain
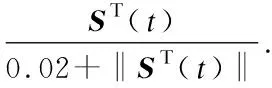
1) Considering the convergence speed of the state trajectories, it clearly shows that the speed of convergence by our method is faster than that of the method given in Ref.[10].
2) As for VSC, the chattering effect is an important aspect that needs concern. In the simulation results, we can confirm that compared with the sliding surface[10], the evolution of the sliding surface in this paper shows that the chattering effect is better suppressed.
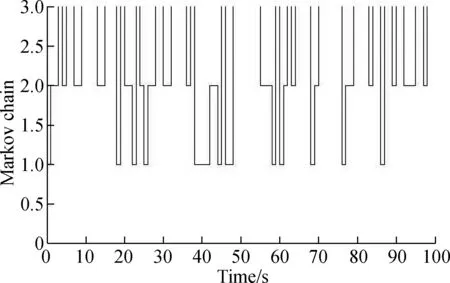
(b)Fig.3 State responses. (a) Closed loop system;(b) Markov chain
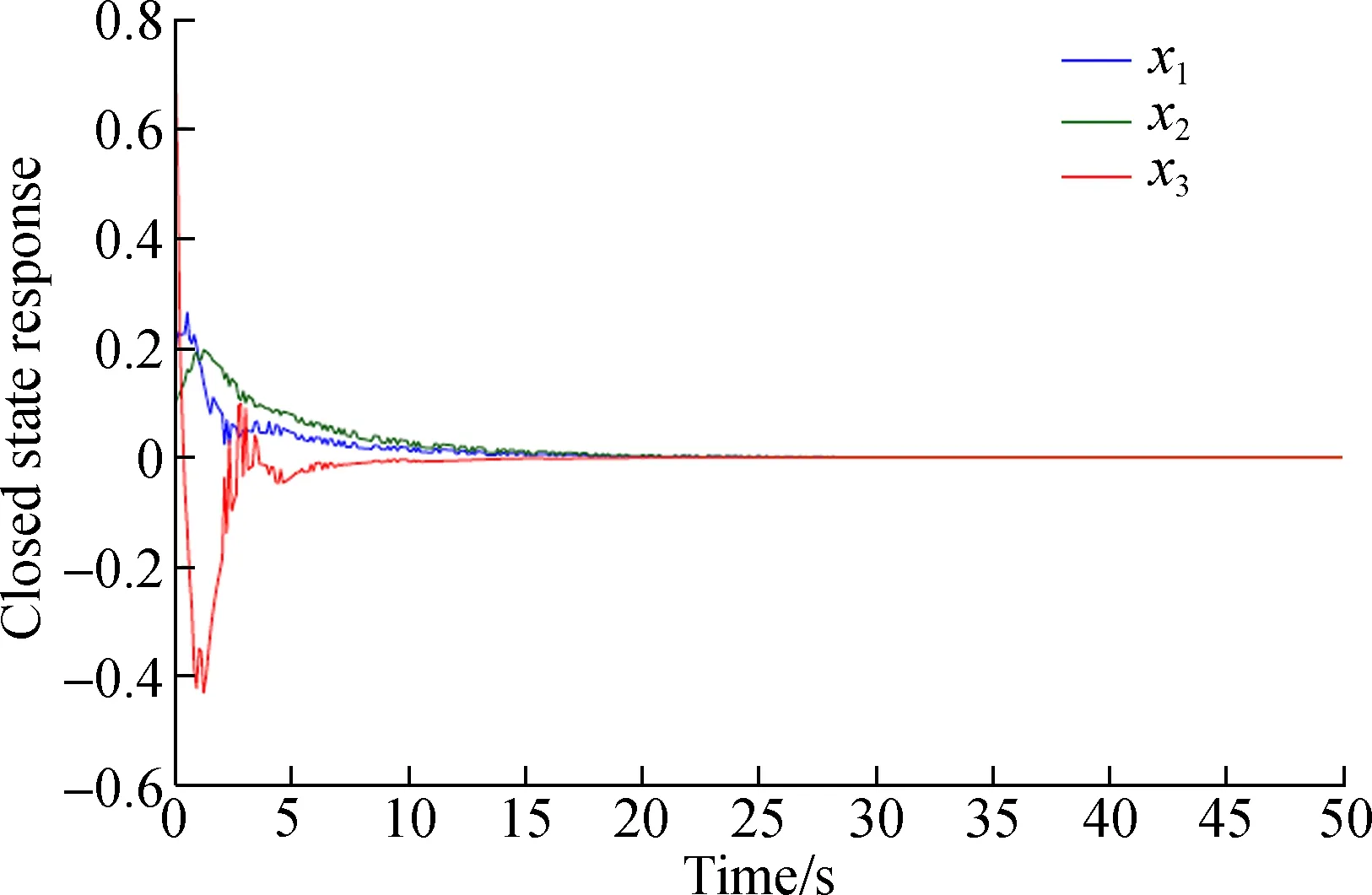
Fig.4 Simulation results of the example by using the method proposed in Ref.[10]
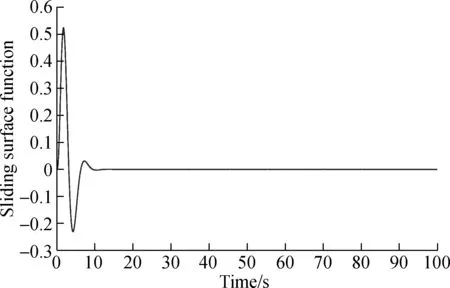
Fig.5 Sliding surface function
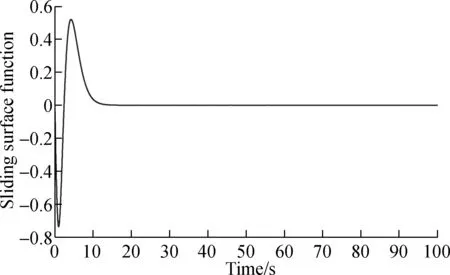
Fig.6 Dynamic sliding mode controller
3) From Fig.4, we can see that the fluctuation of the state trajectories seems acute, but from Fig.3, we can see that the state trajectories are smoother than the results in Ref.[10]. This point deserves mentioning in the process of practical application, and the systems may be damaged if the convergence is too steep.
4) From Fig.4, we can see that the overshoots of the state trajectories are large, but from Fig.3, we can see that the overshoots of state trajectories are smaller than the results in Ref.[10].
From the simulation results, it is clear to see that the state trajectories of the resultant closed-loop system are driven onto the desired sliding surface in finite time, which confirms our proposed method. Also, the simulations sufficiently illustrate that our methods are advanced and correct. As is known to all, in the actual engineering system, stability, convergence speed and overshoot must be considered. In this paper, the sliding surface function and controller are improved in the above aspects.
4 Conclusion
This paper investigates the dynamic VSC problems for DMJSs with PUTPs. We propose a sufficient condition according to precise LMIs to ensure the stochastic admissibility of DMJSs with PUTPs and to construct a dynamic sliding mode controller, which can guarantee the reachability of the state trajectories to the pre-specified sliding surface in finite time despite of the uncertainties and disturbances. Finally, a practical example of a DC motor is provided to demonstrate the effectiveness of the acquired results.
In the existing literature, time delay and packet loss in the network control systems are modeled as a process of using time stamp technology, but for the convenience of research, the existing literature is still based on the hypothesis that the transition probability is completely known. Due to the common existence of network in practical engineering, it is a meaningful topic to combine the DMJSs with PUTPs and network control.
 Journal of Southeast University(English Edition)2018年4期
Journal of Southeast University(English Edition)2018年4期
- Journal of Southeast University(English Edition)的其它文章
- Failure load prediction of adhesive joints under different stressstates over the service temperature range of automobiles
- Effect of fiber type on the bending and uniaxial tensile properties of high-strength high-ductility cementitious composites
- Effects of secondary water curing on the long-term strength and durability of concrete after steam-autoclave curing
- Multi-target range and velocity measurements of a digital phased array radar system
- Cooperative spectrum sensing algorithm based on bilateral threshold selection against Byzantine attack
- Joint resource allocation scheme based on evolutionary game for mobile edge computing
