Mixed Local-Nonlocal Vector Schr?dinger Equations and Their Breather Solutions?
Rui Fan(范蕊)and Fa-Jun Yu(于發(fā)軍)
School of Mathematics and Systematic Sciences,Shenyang Normal University,Shenyang 110034,China
AbstractTo the best of our knowledge,all nonlinearities in the known nonlinear integrable systems are either local or nonlocal.A natural problem is whether there exist some nonlinear integrable systems with both local and nonlocal nonlinearities,and how to solve this kinds of spectral nonlinear integrable systems with both local and nonlocal nonlinearities.Recently,some novel mixed local-nonlocal vector Schr?dinger equations are presented,which are different from the single local and nonlocal coupled Schr?dinger equation.We investigate the Darboux transformation of mixed local-nonlocal vector Schr?dinger equations with a spectral problem.Starting from a special Lax pairs,the mixed localnonlocal vector Schr?dinger equations are constructed.We obtain the one-and two-and N-soliton solution formulas of the mixed local-nonlocal vector Schr?dinger equations with N-fold Darboux transformation.Based on the obtained solutions,the propagation and interaction structures of these multi-solitons are shown,the evolution structures of the one-solitons are exhibited,the overtaking elastic interactions among the two-breather solitons are considered.We find that unlike the local and nonlocal cases,the mixed local-nonlocal vector Schr?dinger equations have some novel results.The results in this paper might be helpful for understanding some physical phenomena described in plasmas.
Key words:mixed-local-nonlocal Schr?dinger equation,soliton solutions,Darboux transformation
1 Introduction
On the basis of Bender and Boettcher,[1?2]the PT-symmetry plays a crucial role in the spectrum of the Hamiltonian. Solving solition equation is an important part in the natural science research.More scholars know that the nonlinear integrable systems are either local or nonlocal.So,naturally the next problem is whether there exist some nonlinear integrable systems with both local and nonlocal nonlinearities.[3?6]The PT-symmetric integrable local and nonlocal vector nonlinear Schr?dinger(NLS)equations are formulated with matrix Lax pairs in Ref.[7].Some novel soliton solutions of the 2-dimensional NLS equation with a PT-symmetric potential can be extended to the equations with two or more spatial variables.[8]The discrete and coupled nonlocal NLS equations are solved via the Darboux transformation in Ref.[9],and some dynamics of higher-order rational solitons of the nonlocal NLS equation are explained with generalized Darboux transformation in Ref.[10].Some discrete rogue-wave solutions with PT-symmetric potential of Ablowitz-Musslimani equation are derived by Yu in Ref.[11].The generalized three coupled Gross-Pitaevskii equations are worked by means of the Darboux transformation and Hirota’s method,several non-autonomous matter-wave solitons including dark-dark-dark and brightbright-bright shapes are obtained in Ref.[12].The nonlocal NLS equation with nonzero boundary conditions is investigated with inverse scattering transform in Ref.[13].An algebraic iterative algorithm is provided to obtain a series of analytic solutions for the discrete PT-symmetric nonlocal NLS equation in Ref.[14].Zhou considered the Darboux transformations and global solutions for a nonlocal derivative NLS equation,which can be globally defined and bounded for all(x,t)in Ref.[15].Integrability of a general integrable nonlocal coupled NLS equation is conf i rmed,some dynamics and interactions of different kinds of solitons are discussed by Zhu in Ref.[16].Yan presented a method to construct some novel two-family-parameter equations,including the local,nonlocal,and mixed-localnonlocal vector NLS equations.[17]
With the further study of the soliton theory,it provides many methods for solving nonlinear partial differential equations,such as the homogeneous balance method,[18]bilinear method,[19]traveling wave method,[19]Darboux transformation(DT)method,[20]inverse scattering transform method.[19?22]The Darboux transformation can get a new solution from a known equation,some multi-soliton solutions of the nonlinear partial differential equation can be obtained through multiple Darboux transformation.For examples,some bright,dark and breather wave soliton solutions of the super-integrable hierarchy presented by using Darboux transformation.[23]The non-autonomous multi-rogue wave solutions in a spin-1 coupled nonlinear Gross-Pitaevskii equation with varying dispersions,higher nonlinearities,gain/loss and external potentials are investigated in Ref.[24].The generalized three-coupled Gross Pitaevskii equations by means of the DT and Hirota’s method are worked,several non-autonomous matter-wave solitons including dark-dark-dark and bright-bright-bright shapes are obtained in Refs.[24–25].The non-autonomous discrete vector bright-dark solutions and their controllable behaviors in the coupled Ablowitz-Ladik equation with variable coefficients are considered in Ref.[25].The Darboux transformation method with 4×4 spectral problem are applied to a specific equation and then the explicit solutions of the lattice integrable coupling equation are obtained in Refs.[26–27].
To the best of our knowledge,all nonlinearities in the known nonlinear integrable systems are either local or nonlocal.There are few work to solve some nonlinear integrable systems with both local and nonlocal nonlinearities.Therefore,we will investigate the Darboux transformation of the mixed local-nonlocal vector Schr?dinger equations with a spectral problem,and obtain the one-and two-and N-soliton solution formulas of the mixed localnonlocal vector Schr?dinger equations equation with N-fold Darboux transformation.Based on the obtained solutions,we find that unlike the local and nonlocal cases,the mixed local-nonlocal vector Schr?dinger equations have some novel results.
This paper is organized as follows:In Sec.2,we construct Darboux transformation for mixed local-nonlocal vector Schr?dinger equations,and derive the proofs of the Darboux transformation procedure.In Sec.3,we apply the Darboux transformation to mixed local-nonlocal vector Schr?dinger equations and obtain N-soliton solution formula.The evolutions of the intensity distribution of the soliton solutions are illustrated.
2 Darboux Transformation for Mixed Local-Nonlocal Vector Schr?dinger Equations
More scholars know that the nonlinear integrable systems are either local or nonlocal.So,naturally the next problem is whether there exist some nonlinear integrable systems with both local and nonlocal nonlinearities,how to solve this kinds of spectral nonlinear integrable systems with both local and nonlocal nonlinearities.
In this paper,we use two families parameters system to find new mixed-local-nonlocal systems and derive some exact solutions for mixed local-nonlocal vector Schr?dinger equations.In next content,we find novel mixed-localnonlocal vector NLS equations,i.e.,the q1-nonlocal-q2-local systems in Ref.[28].

we first consider the linear iso-spectral system

here Ψ =(ψ1(x,t),ψ2(x,t),ψ3(x,t))T,is a 3 × 1 column complex-valued eigenvector function,λ∈C is an isospectral parameter,the generalized Pauli matrix Σ3and potential matrix U are defined by
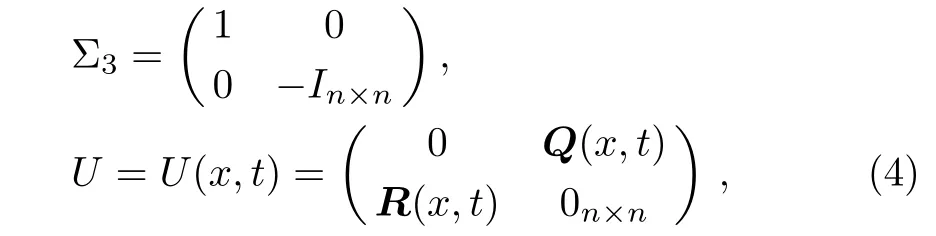
where In×nand 0n×nare n × n unity and zero matrixes,respectively,R(x,t)=(r1(x,t),r2(x,t),...,rn(x,t))and Q(x,t)= (q1(x,t),q2(x,t),...,qn(x,t))Tare complexvalued row vector functions.The compatibility condition of Eqs.(2)and(3),Ψxt= Ψtx,i.e.,zero-curvature equation,leads to the 2n-component coupled nonlinear wave system

Here we consider one of these cases:in order to simplify the equation,we make σ1= σ2=1,and Σ3=and introduce a new one-family-parameter ?xj= ±1,j=1,2,3,...,n,symmetry reduction

which make system(5)generate the above-introduced new local-nonlocal vector equations(1)with ?xj= ±1,?tj=1,that is,Eq.(1)with ?xj= ±1 and ?tj=1 adm-its the Lax pair given by Eqs.(2)and(3)with the new symmetric constraint(6).
Therefore,we can get a novel Lax pairs with R(x,t)=(r1(x,t),r2(x,t))and Q(x,t)=(q1(x,t),q2(x,t))Tin Eq.(5)we can find that the zero-curvature equation can lead to Eq.(1)under the condition of compatibility.


Next,we construct the Darboux transformation of mixed local-nonlocal vector Schr?dinger equation with the Lax pairs of Eqs.(7)and(8),which are satisfied with the 3×3 transformation matrices of φ,,and.We consider the isospectral problem of mixed local-nonlocal vector Schr?dinger equation and recommend a gauge transformation T of the Lax pairs of Eqs.(7)and(8):
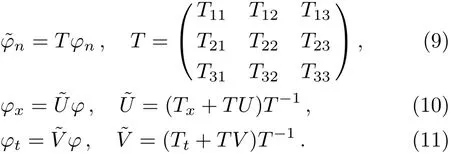
Let ψ = (ψ1,ψ2,ψ3)T, ? = (?1,?2,?3)T,X =(X1,X2,X3)Tare three basic solutions of the systems Eqs.(7)and(8),then we give the following linear algebraic systems:

with

where λjandshould choose appropriate parameters,thus the determinants of coefficients for Eq.(13)are nonzero.
Defining a 3×3 matrix T,and T is of the form as the following


where N is a natural number,the(m,n=1,2,3)are the functions of x and t.Through calculations,we can obtain?T as the following

which proves that λj(j=1 ≤ j ≤ 3N)are 3N roots of?T.Based on these conditions,we will proof that theandhave the same forms with U and V,respectively.Proposition 1The matrixdefined by Eq.(10)has the same type as U,that is,

and in which the transformation formulas between old and new potentials are shown on as the following

The transformations(17)are used to get a Darboux transformation of the spectral problem(10).
Proof By assuming T?1=T?/?T and

it is easy to verify that Bsl(1≤s,l≤3)are 3N-order or 3N+1-order polynomials in λ.
Through some accurate calculations,λj(1≤ j≤ 3,)are the roots of Bsl(1≤s,l≤3).Thus,Eq.(18)has the following structure

where


Through comparing the coefficients of λ in Eq.(21),we can obtain

In the following section,we assume that the new matrixhas the same type with U,which means that they have the same structures only of of U transformed into.After careful calculation,we compare the ranks of λN,and get the objective equations as the following:of.From Eqs.(17)and(24),we know that=F(λ).The proof is completed.
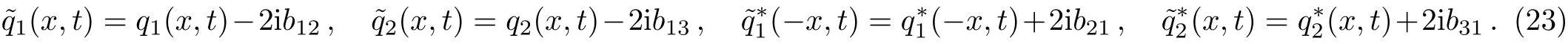
From Eqs.(16)and(17),we know that=C(λ).The proof is completed.
Proposition 2Under the transformation(23),the matrixdefined by Eq.(11)has the same form as V,that is,

ProofWe assume the new matrixalso has the same form with V.If we obtain the similar relations betweenin Eq.(17),we can prove that the gauge transformations under T turn the Lax pairs U,V into new Lax pairs,with the same types.
By assuming T?1=T?/?T and

It is easy to verify that Esl(1 ≤ s,l≤ 3)are 3N+1-order or 3N+2-order polynomials in λ.
Through some calculations,λj(j=1≤j≤3,)are the roots of Esl(s,l=1≤j≤3).Thus,Eq.(25)has the following structure

where
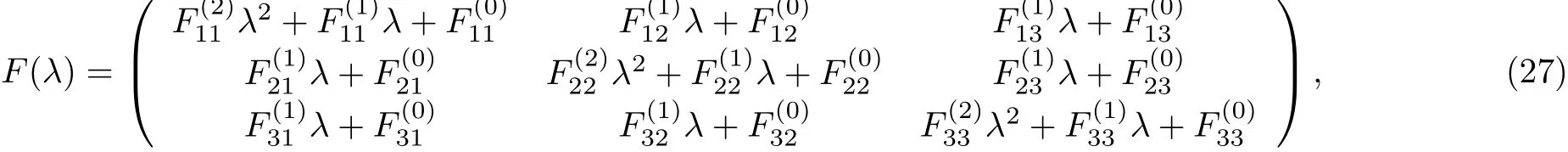

Through comparing the coefficients of λ in Eq.(28),we get the objective equations as the following:

In the above section,we assume the new matrixhas the same type with V,which means they have the same structures onlyof V transformed into
3 Breather Solutions for the Mixed Local-Nonlocal Vector Schr?dinger Equation
In order to make the seed solutions satisfy Eq.(1),so we choose a set of seed solutions q1(x,t)=q2(x,t)=and substitute the solutions into Eqs.(2)and(3),we will get three basic solutions for these equations:

Substituting Eq.(30)into Eq.(13),we obtain

In order to calculate the soliton solution,we consider N=1 in Eqs.(14)and(15),and obtain the matrix T

According to Eq.(33),we get

Based on Eqs.(13)and(31),we can obtain the following systems
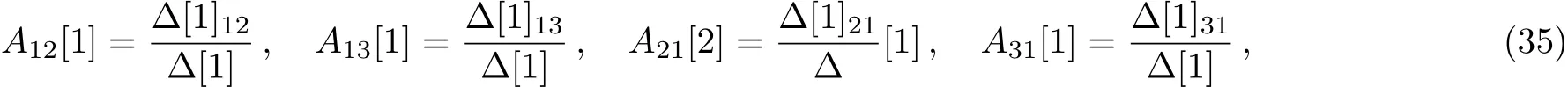
the analytic soliton solutions of mixed local-nonlocal vector Schr?dinger equation are obtained by the DT method as the following
He stood there for a long time, until he heard her moving quietly. He found her sitting on the edge of their bed, her head bent, her hands gripping the mattress76.
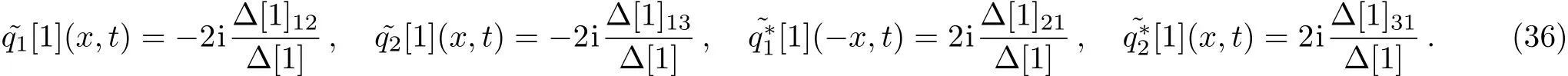
To illustrate the wave propagations of the obtained one-soliton solutions(36),we can choose these free parameters in the forms λ1,λ2,λ3,Fmk(m=1,2,3,k=1,2,3)and the intensity distributions for the soliton solutions given by Eq.(36)are illustrated in Fig.1.From the single soliton,we can find that the amplitude of the breather soliton grows and decays with time depending on the parameters λ1,λ2,λ3,Fmk(m=1,2,3,k=1,2,3).
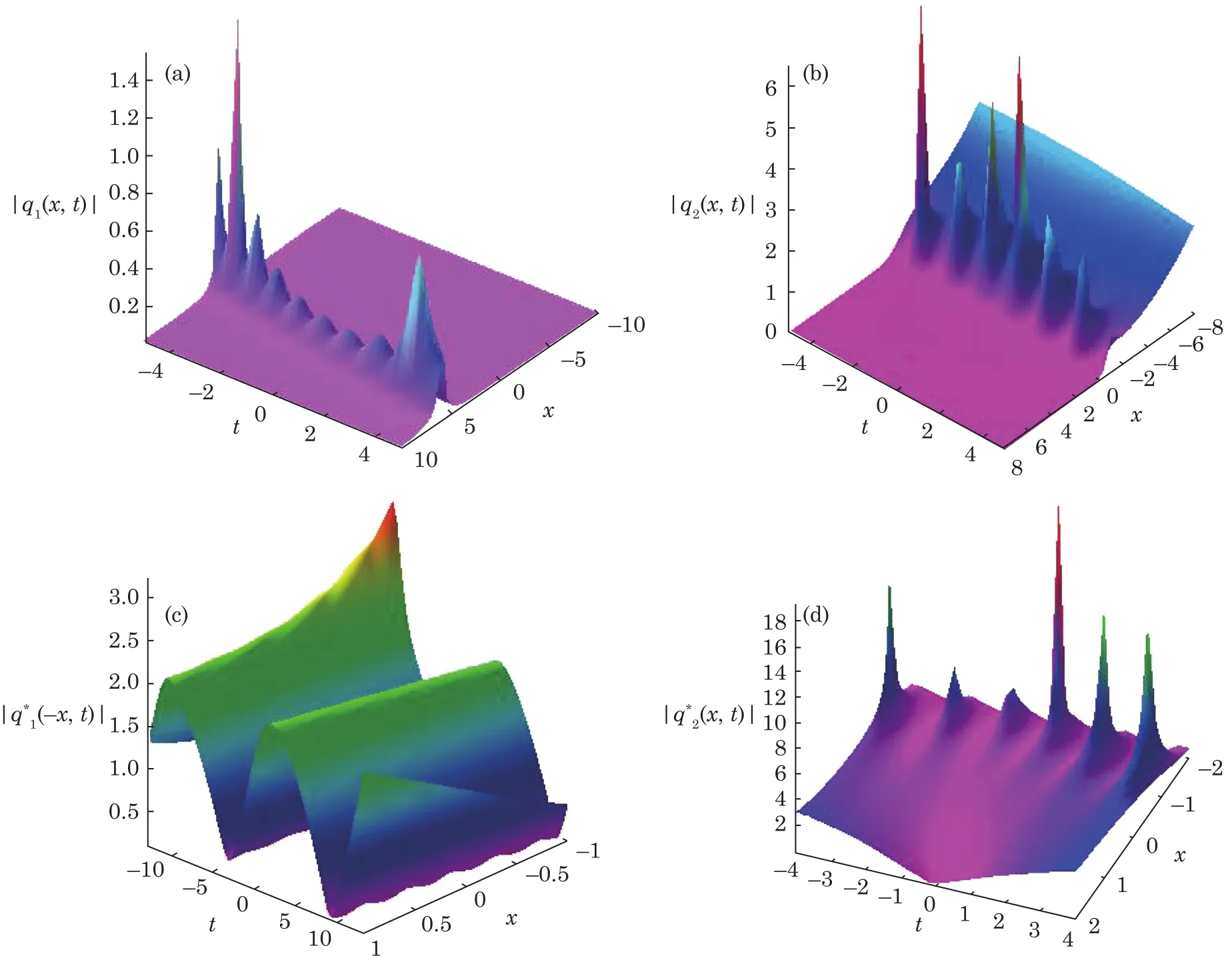
Fig.1(Color online)Pro files of(a)the intensity distributionof Eq.(36);(c)the intensity distributionof Eq.(36)with λ1=0.15, λ2=0.25, λ3=0.35,F11=1,F22=2i,F12=2i,F21=1,F31=1,F32=i,(b)the intensity distributionof Eq.(36);(d)the intensity distributionof Eq.(36)with λ1=0.1i,λ2=i,λ3=0.3i,F11=i,F22=2i,F12=2i,F21=1,F31=1,F32=i.
Now we consider N=2 in Eqs.(13)and(14),and obtain the following system

where i=0,1,2.and j=1,2,3,4,5,6.According to Eq.(37)and Cramer’s rule,we can yield
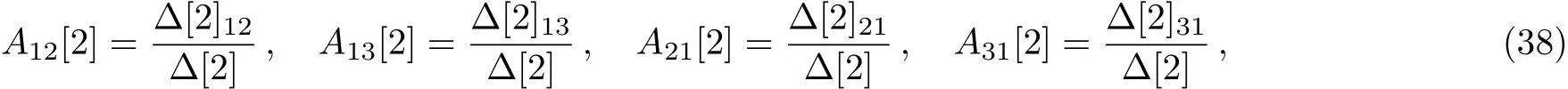
the analytic two-soliton solutions of mixed local-nonlocal vector Schr?dinger equation are obtained by the DT method as the following

We know

and

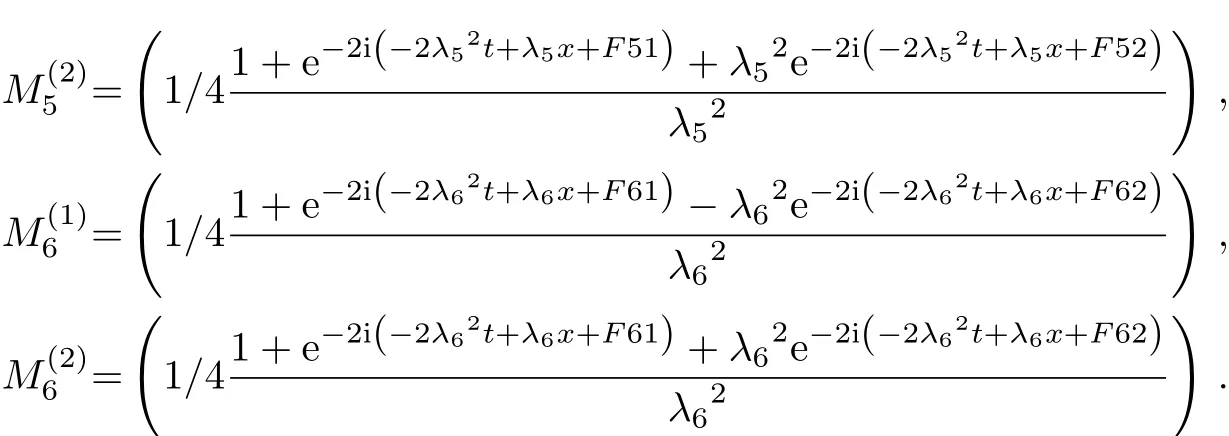
In order to obtain the N-soliton solution formula of the mixed local-nonlocal vector Schr?dinger equation,we consider N=n in Eq.(14),take i=0,1,2,3,...,n?1 and j=1,2,3,...,3n into Eq.(15).We use same way to get the form of N-soliton solution formula

and

We can obtain some solutions for linear systems via the Cramer’s rule

with
where

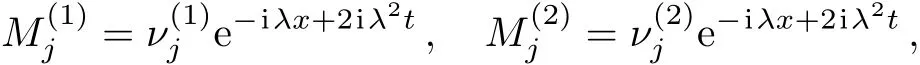

Based on Eqs.(13)and(31),we can obtain the following systems the analytic N-soliton solutions of mixed local-nonlocal vector Schr?dinger equations are obtained by the Darboux transformation method as the following

In this paper,Figs.1 and 2 exhibit the exact one-and two-breather soliton solutions of Eq.(1),similar to the one-soliton solution,we obtain the N-soliton solution formula of the mixed local-nonlocal vector Schr?dinger equation with N-fold Darboux transformation.Based on the obtained solutions,the propagation and interaction structures of these multi-solitons are shown graphically:Fig.1 exhibit the evolution structures of the one-breather solitons with N=1;Fig.2,the overtaking elastic interactions among the two-breather solitons with N=2.The results in this paper might be helpful for understanding some physical phenomena described in plasmas.Notice that the above-mentioned wave structures for the nonlocal coupled NLS equations did not appear in the usual(local)coupled NLS equations.Form the viewpoint of wave structures,the nonlocal and local models are of distinct characteristics.
In order to verify the analytic solutions,we substitute the obtained solutions(36)and(39)into the Eq.(1),and we find that the solutions(36)and(39)satisfy the mixed-local-nonlocal vector NLS equations,i.e.,the q1-nonlocal-q2-local systems.And we will test the validity of the analytic solutions by numerical simulations of the initial equations in the future paper.
4 Conclusions
In this paper,we give the form of N-soliton solution of mixed local-nonlocal vector Schr?dinger equation with Darboux transformation.In addition,the one-soliton and two-soliton solutions are solved in detail. At present,few of the mixed local-nonlocal vector Schr?dinger equation are studied by the Darboux transformation,we obtain the one-and two-and N-soliton solution formulas of the mixed local-nonlocal vector Schr?dinger equation with N-fold Darboux transformation.Based on the obtained solutions,the propagation and interaction structures of these multi-solitons are shown,the evolution structures of the one-dark and one-breather solitons are exhibited with N=1,the overtaking elastic interactions among the twobreather solitons are considered with N=2.These results might be helpful for understanding physical phenomena in a nonlinear diffusion regularity of two nonlinear wave propagation in the medium,and can be applied widely in the field of nonlinear optics,and also play an important role in meteorology.
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
- Communications in Theoretical Physics的其它文章
- Electron Transport Properties of Graphene-Based Quantum Wires?
- Magnetic Properties of XXZ Heisenberg Antiferromagnetic and Ferrimagnetic Nanotubes?
- On the Singular Effects in the Relativistic Landau Levels in Graphene with a Disclination?
- Super-sensitivity in Dynamics of Ising Model with Transverse Field:From Perspective of Franck-Condon Principle?
- New Feedback Control Model in the Lattice Hydrodynamic Model Considering the Historic Optimal Velocity Di ff erence Effect?
- A Class of Rumor Spreading Models with Population Dynamics?
