張虎 邢成芬 龍克文 肖亞寧 陶坤 王利晨 龍毅

1)(北京科技大學(xué)材料科學(xué)與工程學(xué)院,北京 100083)

2)(佛山市程顯科技有限公司,佛山 528513)

3)(佛山市川東磁電股份有限公司,佛山 528513)

4)(首都師范大學(xué)物理系,北京 100048)

磁熵變(?SM)與磁場(chǎng)(μ0H)的相關(guān)性已在很多二級(jí)相變材料中被研究并報(bào)道,但一級(jí)相變材料的磁熱效應(yīng)與磁場(chǎng)相關(guān)性還少有報(bào)道.本文在具有一級(jí)磁結(jié)構(gòu)相變的Mn0.6Fe0.4NiSi0.5Ge0.5材料中研究發(fā)現(xiàn)?SM與μ0H存在線性相關(guān)性,并通過(guò)麥克斯韋關(guān)系式的數(shù)值分析詳細(xì)討論了這一線性相關(guān)性的來(lái)源.同時(shí),進(jìn)一步發(fā)現(xiàn)在低磁場(chǎng)時(shí),?SM近似正比于μ0H的平方.該線性相關(guān)性同樣在一級(jí)磁結(jié)構(gòu)相變Ni50Mn34Co2Sn14材料中得到了印證.但由于一級(jí)磁彈相變LaFe11.7Si1.3材料相變溫度具有更強(qiáng)的磁場(chǎng)依賴(lài)性,不具有?SM的線性相關(guān)性,因此,本研究表明,當(dāng)磁結(jié)構(gòu)相變材料的相變溫度具有弱磁場(chǎng)依賴(lài)性時(shí),?SM與μ0H具有線性相關(guān)性.進(jìn)而,在磁場(chǎng)未達(dá)到相變飽和磁場(chǎng)以下,利用?SM與μ0H的線性相關(guān)性可以有效推測(cè)更高磁場(chǎng)下的?SM.

1 引 言

與傳統(tǒng)的氣體壓縮制冷技術(shù)相比,基于磁熱效應(yīng)(magnetocaloric ef f ect,MCE)的磁制冷技術(shù)具有環(huán)境友好和節(jié)能高效等優(yōu)點(diǎn),因此受到廣泛的關(guān)注[1?4].磁熱效應(yīng)可以由等溫磁熵變(?SM)和絕熱溫變(?Tad)兩種參數(shù)來(lái)表征[5].通常,磁制冷材料可以分為一級(jí)磁相變材料和二級(jí)磁相變材料[6].許多一級(jí)磁相變材料表現(xiàn)出大的磁熱效應(yīng)[7?11],但其磁熱效應(yīng)的工作溫區(qū)往往很窄,且常伴有大的磁滯和熱滯,這會(huì)大幅降低材料的制冷效率[12,13].相反,二級(jí)磁相變材料雖然磁熱效應(yīng)相對(duì)低,但其工作溫區(qū)大且沒(méi)有磁滯和熱滯,使其在寬溫區(qū)內(nèi)具有大的磁制冷能力[14,15].因此,兩種磁相變材料各有優(yōu)缺點(diǎn),近年來(lái)都被進(jìn)行了廣泛的研究[1,16].

無(wú)論從基礎(chǔ)研究還是實(shí)際應(yīng)用的角度,磁熱效應(yīng)與磁場(chǎng)的相關(guān)性都具有非常重要的意義,因?yàn)樗粌H能夠指導(dǎo)我們更好地理解和優(yōu)化磁熱效應(yīng),還能夠幫助我們估測(cè)更高磁場(chǎng)下的磁熱效應(yīng)[6,17].利用平均場(chǎng)模型,Oesterreicher和Parker[18]推導(dǎo)出二級(jí)磁相變材料居里溫度TC附近?SM與磁場(chǎng)的相關(guān)性可以表達(dá)為|?|∝ Hn,其中n=2/3.但后來(lái)發(fā)現(xiàn),一些二級(jí)磁相變材料中n值明顯偏離了2/3[19?21].Franco等[19,22]進(jìn)一步證明二級(jí)磁相變材料中n=1+(1/δ)[1? (1/β)],其中δ和β是臨界指數(shù).并且,他們提出了一個(gè)唯象的“通用曲線”,可以用來(lái)有效地預(yù)測(cè)磁熱效應(yīng)和判斷相變性質(zhì)[15,23].但另一方面,由于一級(jí)磁相變的復(fù)雜性和多樣性,針對(duì)一級(jí)磁相變材料磁熱效應(yīng)和磁場(chǎng)的相關(guān)性研究還相對(duì)較少[17,24].

MM′X(M,M′為過(guò)渡族元素,X為主族元素)合金是一種新型磁制冷材料,因發(fā)生順磁Ni2In型六角相到鐵磁TiNiSi型正交相的一級(jí)磁結(jié)構(gòu)相變,表現(xiàn)出大磁熱效應(yīng),故受到越來(lái)越多的關(guān)注.近期,研究發(fā)現(xiàn)MM′X合金存在?SM和磁場(chǎng)μ0H的線性相關(guān)性[25,26],然而這一線性相關(guān)性的內(nèi)在原因尚不清楚.本工作以具有一級(jí)磁結(jié)構(gòu)相變的MM′X合金為基礎(chǔ),詳細(xì)研究了一級(jí)磁結(jié)構(gòu)相變材料的?SM和μ0H的相關(guān)性,分析了產(chǎn)生線性相關(guān)性的內(nèi)在機(jī)制,并對(duì)比了該線性相關(guān)性對(duì)其他一級(jí)磁結(jié)構(gòu)/磁彈相變材料的適用性.

2 實(shí) 驗(yàn)

將純度大于99.9 wt.%的組成元素按Mn0.6Fe0.4NiSi0.5Ge0.5,Ni50Mn34Co2Sn14,LaFe11.7Si1.3的化學(xué)成分進(jìn)行配比,在氬氣保護(hù)氣氛下進(jìn)行電弧熔煉.將熔煉好的鑄錠密封在充有高純氬氣的石英管中進(jìn)行退火處理,其中Mn0.6Fe0.4NiSi0.5Ge0.5鑄錠在1123 K退火5 d并爐冷至室溫,Ni50Mn34Co2Sn14在1173 K退火4 d并冰水淬火,LaFe11.7Si1.3在1373 K退火40 d并冰水淬火.室溫X射線衍射(X-ray dif f raction,XRD)實(shí)驗(yàn)確認(rèn),除LaFe11.7Si1.3存在少量α-Fe第二相外(約4.4 wt.%),所有樣品均形成了單相.采用MPMS SQUID VSM磁性測(cè)量設(shè)備對(duì)材料的熱磁曲線和等溫磁化曲線進(jìn)行了測(cè)試,為了避免出現(xiàn)“偽巨磁熵變?SM”[27,28],M-μ0H測(cè)量采用loop模式,即每條M-μ0H曲線測(cè)試前,先將樣品加熱至完全順磁態(tài),然后降溫至目標(biāo)測(cè)試溫度[29,30].此外,M-μ0H曲線還進(jìn)行了退磁校正,即Hint=Hext?NdM.

3 結(jié)果與討論

圖1(a)所示為Mn0.6Fe0.4NiSi0.5Ge0.5在不同磁場(chǎng)變化下的等溫磁熵變??SM隨溫度變化的關(guān)系.由圖1(a)可以看出,Mn0.6Fe0.4NiSi0.5Ge0.5表現(xiàn)出巨磁熱效應(yīng),5 T磁場(chǎng)下在315 K的最大磁熵變??SM為38.0 J/(kg·K).這一巨磁熱效應(yīng)歸因于從順磁Ni2In型六角相到鐵磁TiNiSi型正交相的一級(jí)磁結(jié)構(gòu)相變[25].為進(jìn)一步研究??SM的磁場(chǎng)相關(guān)性,圖1(b)繪出了??SM峰值與磁場(chǎng)μ0H的依賴(lài)關(guān)系.可以看出當(dāng)μ0H>1 T時(shí),??SM與磁場(chǎng)存在線性依賴(lài)關(guān)系:

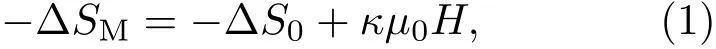
其中??S0為零磁場(chǎng)時(shí)的截距,κ是描述??SM對(duì)磁場(chǎng)依賴(lài)性的斜率.線性擬合的校正R方因子為0.99834,表明?SM-μ0H曲線具有很好的線性依賴(lài)關(guān)系.但同時(shí)發(fā)現(xiàn),在低場(chǎng)下出現(xiàn)了一定的偏差(圖1(b)插圖).下面將通過(guò)數(shù)值分析詳細(xì)討論高場(chǎng)下的線性相關(guān)性和低場(chǎng)下偏差出現(xiàn)的原因.

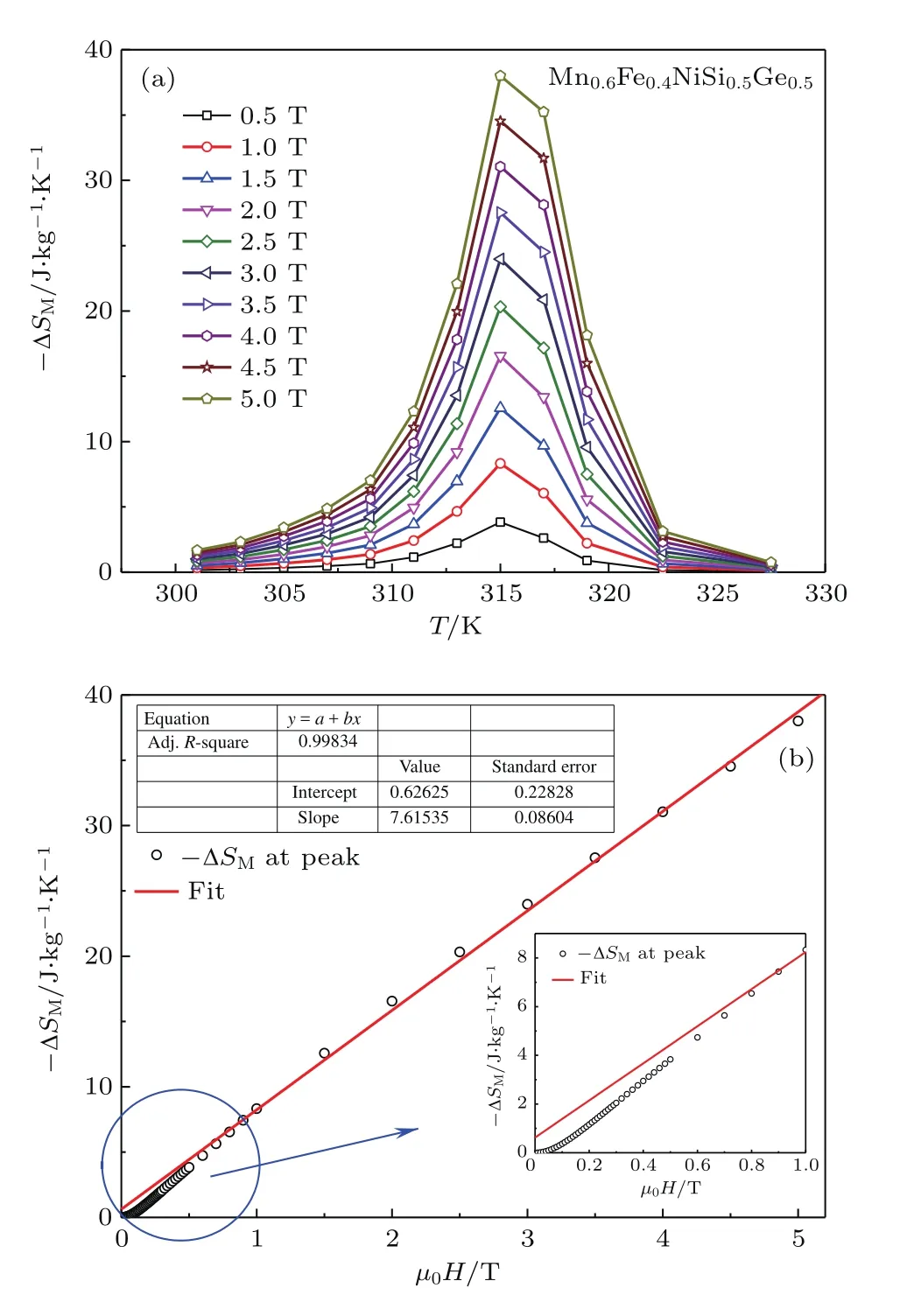
圖1 (a)不同磁場(chǎng)變化下Mn0.6Fe0.4NiSi0.5Ge0.5的等溫磁熵變??SM隨溫度的變化關(guān)系;(b)??SM峰值與磁場(chǎng)μ0H的依賴(lài)關(guān)系及線性擬合,插圖為低場(chǎng)部分的線性擬合偏差Fig.1.(a)Temperature dependence of??SMfor Mn0.6 Fe0.4NiSi0.5Ge0.5compound under dif f erent magnetic f i eld changes;(b)??SMvalue at peak as a function ofμ0H,and the f i tting line to ??SM-?μ0H curve(the inset shows the??SM-?μ0H curve and the f i tting line at low f i elds).

圖2(a)所示為Mn0.6Fe0.4NiSi0.5Ge0.5的等溫磁化曲線.在居里溫度TC=312 K附近,磁化曲線在低場(chǎng)時(shí)隨磁場(chǎng)迅速增加并趨于飽和,然后當(dāng)μ0H>1 T時(shí)出現(xiàn)大的上升,表明發(fā)生了磁場(chǎng)誘導(dǎo)的從順磁Ni2In型六角相到鐵磁TiNiSi型正交相的變磁轉(zhuǎn)變.同時(shí),大的磁滯說(shuō)明該相變性質(zhì)為一級(jí)相變.根據(jù)等溫磁化曲線,可以利用麥克斯韋關(guān)系式計(jì)算等溫磁熵變?6

,31]:

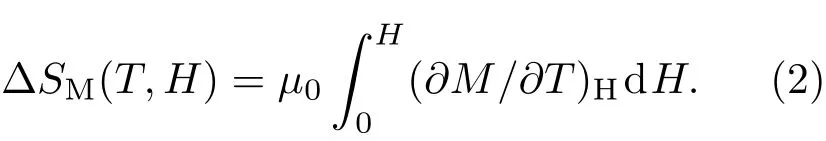
近些年,由于采用麥克斯韋關(guān)系式計(jì)算一級(jí)磁相變材料的磁熵變常常出現(xiàn)“偽巨磁熵變?SM”,因此,其是否適用于一級(jí)相變磁熵變的計(jì)算存在很多爭(zhēng)論[28,32?34].近期,Amaral等[35,36]發(fā)現(xiàn)麥克斯韋關(guān)系式產(chǎn)生“偽巨磁熵變?SM”不是一級(jí)磁相變性質(zhì)造成的,而是由于沒(méi)有考慮兩相共存的非平衡態(tài)以及測(cè)試過(guò)程對(duì)不同磁性的影響.進(jìn)而,Caron等[1,29]指出,通過(guò)采用loop模式測(cè)試等溫磁化曲線能夠避免“偽巨磁熵變?SM”的出現(xiàn),因此,麥克斯韋關(guān)系式仍適用于一級(jí)磁相變.因?yàn)榈葴卮呕€是在不連續(xù)的溫度點(diǎn)下測(cè)得,所以麥克斯韋關(guān)系式可以近似為[12,31]

其中?M為磁場(chǎng)Hi下降場(chǎng)磁化曲線M316K和M314K之間的差值.圖2(b)所示為?M/2與磁場(chǎng)的變化關(guān)系.根據(jù)(3)式,315 K時(shí)的磁熵變?SM應(yīng)為?M/2-μ0H曲線的面積積分.由圖2(b)可知,低場(chǎng)時(shí)由于鐵磁相的磁化強(qiáng)度迅速增大導(dǎo)致?M/2快速上升,隨后在到達(dá)一個(gè)峰值后?M/2開(kāi)始緩慢下降.以該峰值?Mmax/2為界可將?SM分為兩部分,第一部分?SM1可以近似看為三角形,特別是在0.2 T以下斜率接近為常數(shù).因此,?SM1可以近似用如下表達(dá)式計(jì)算:

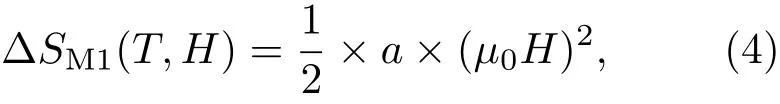
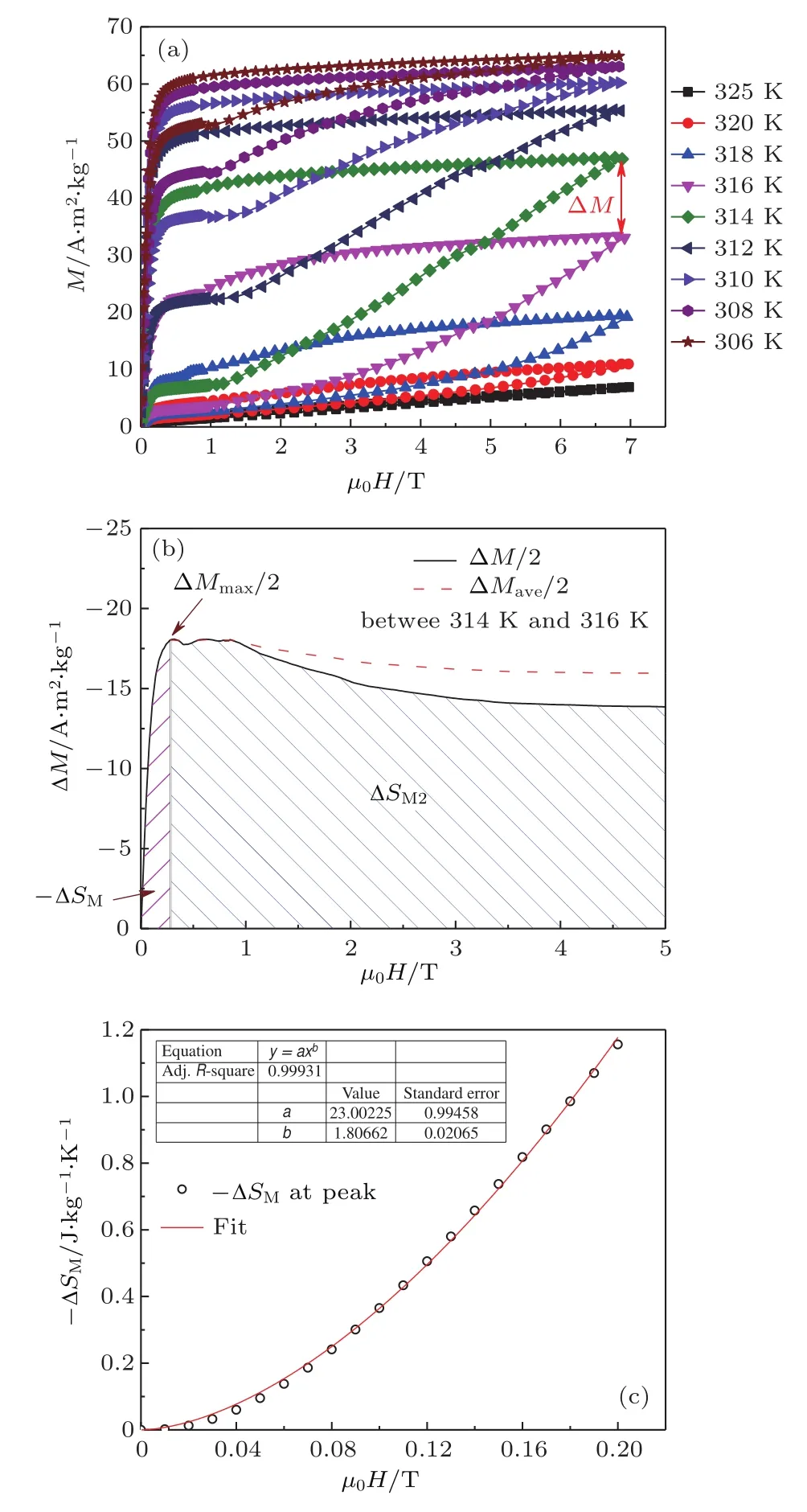
圖2 (a)不同溫度下Mn0.6Fe0.4NiSi0.5Ge0.5的等溫磁化曲線;(b)314 K和316 K之間?M/2與磁場(chǎng)μ0H的變化關(guān)系;(c)0.2 T磁場(chǎng)以下磁熵變??SM峰值與磁場(chǎng)的依賴(lài)關(guān)系及指數(shù)擬合Fig.2.(a)Magnetization isotherms of Mn0.6Fe0.4NiSi0.5 Ge0.5compound in loop process;(b)?M/2 between 314 K and 316 K as a function of magnetic fi eldμ0H;(c)magnetic if eld dependence of??SMvalue at peak and the fi tting line at fi elds below 0.2 T.

其中a是該三角形的斜率.由(4)式可以看出,當(dāng)a是常數(shù)時(shí),|?SM1|∝ H2.圖2(c)為0.2 T磁場(chǎng)以下磁熵變??SM峰值與磁場(chǎng)的依賴(lài)關(guān)系及指數(shù)擬合.該曲線符合非線性指數(shù)擬合條件,磁場(chǎng)μ0H的指數(shù)擬合為1.81,接近2,證明了以上數(shù)值分析的合理性.

當(dāng)磁場(chǎng)大于峰值?Mmax/2的臨界場(chǎng)μ0H?Mmax/2時(shí),?SM= ?SM1max+?SM2,其中?SM1max是?Mmax/2以下的面積,為一個(gè)定值;而?SM2是μ0H?Mmax/2和最終磁場(chǎng)μ0H之間的積分面積.由圖2(b)可見(jiàn),?SM2可近似看為梯形,因此,可用如下表達(dá)式計(jì)算:

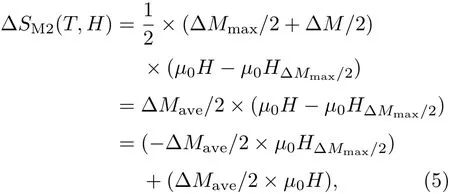
其中?Mave/2是(?Mmax/2+?M/2)的平均值.根據(jù)(5)式,當(dāng)磁場(chǎng)大于μ0H?Mmax/2時(shí),總的磁熵變?SM為

從圖2(b)可以看出,當(dāng)μ0H>1 T時(shí)?Mave/2近似為恒定值.通過(guò)對(duì)比(1)式和(6)式,(6)式中的第一個(gè)括號(hào)可看成(1)式中的??S0,(6)式中的第二個(gè)括號(hào)相當(dāng)于(1)式中的κμ0H.因此,當(dāng)μ0H>1 T時(shí),??SM與磁場(chǎng)存在線性相關(guān)性.

通過(guò)以上數(shù)值分析和討論,闡明了具有一級(jí)磁結(jié)構(gòu)相變的Mn0.6Fe0.4NiSi0.5Ge0.5的?SM-μ0H曲線在高場(chǎng)下的線性相關(guān)性和低場(chǎng)下偏差出現(xiàn)的原因.進(jìn)一步,利用類(lèi)似的數(shù)值分析,我們發(fā)現(xiàn)除了?SM峰值外,其他溫度的?SM值與磁場(chǎng)也存在線性相關(guān)性,如圖3所示.

因此,可以通過(guò)線性擬合的方式推測(cè)高場(chǎng)下的?SM值.例如,通過(guò)插圖中的線性擬合可以獲得7 T磁場(chǎng)下不同溫度的?SM值.圖3所示為7 T磁場(chǎng)變化下Mn0.6Fe0.4NiSi0.5Ge0.5的實(shí)驗(yàn)?SM及擬合?SM曲線.由圖3可見(jiàn),擬合?SM曲線與實(shí)驗(yàn)曲線完全重疊,這一結(jié)果證實(shí),可以利用?SM值與磁場(chǎng)的線性相關(guān)性來(lái)預(yù)測(cè)更高磁場(chǎng)下的磁熵變值.需要指出的是,磁熵變來(lái)自于磁場(chǎng)誘導(dǎo)的相變,當(dāng)磁場(chǎng)達(dá)到一定值后,相變完全,則磁熵變達(dá)到飽和,不再隨磁場(chǎng)增加,線性相關(guān)性將不再存在.因此,該?SM值與磁場(chǎng)的線性相關(guān)性只在磁場(chǎng)未達(dá)到相變飽和磁場(chǎng)以下成立.

?SM與磁場(chǎng)μ0H的線性相關(guān)性在其他具有一級(jí)磁結(jié)構(gòu)相變的MM′X合金中也被發(fā)現(xiàn)報(bào)道[25],本文工作進(jìn)一步驗(yàn)證了該線性相關(guān)性在一級(jí)磁結(jié)構(gòu)相變的MM′X合金中具有普適性.為了進(jìn)一步驗(yàn)證?SM值與磁場(chǎng)的線性相關(guān)性是否也適用于其他一級(jí)磁相變體系,我們進(jìn)一步研究了Ni50Mn34Co2Sn14和LaFe11.7Si1.3的?SM值與磁場(chǎng)μ0H的依賴(lài)關(guān)系(圖4).需要指出的是,Ni50Mn34Co2Sn14經(jīng)歷的是一級(jí)馬氏體磁結(jié)構(gòu)相變,而LaFe11.7Si1.3則為一級(jí)磁彈相變.由圖4可知,Ni50Mn34Co2Sn14的?SM值與磁場(chǎng)μ0H具有很好的線性相關(guān)性,但LaFe11.7Si1.3的?SM-μ0H曲線不符合線性相關(guān)性,這表明?SM值與磁場(chǎng)μ0H的線性相關(guān)性不適用于非磁結(jié)構(gòu)相變體系.

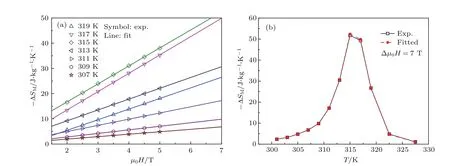
圖3 (a)Mn0.6Fe0.4NiSi0.5Ge0.5在不同溫度下??SM與磁場(chǎng)μ0H的依賴(lài)關(guān)系及線性擬合;(b)7 T磁場(chǎng)變化下Mn0.6Fe0.4NiSi0.5Ge0.5的實(shí)驗(yàn)?SM及擬合?SM曲線Fig.3.(a)??SMvalues at dif f erent temperatures around TCas a function ofμ0H and the f i tting lines to??SM-?μ0H curves for Mn0.6Fe0.4NiSi0.5Ge0.5compound;(b)temperature dependences of experimental and f i tted?SM for under magnetic f i eld change of 7 T for Mn0.6Fe0.4NiSi0.5Ge0.5compound.

由(6)式可知,只有當(dāng)?M隨磁場(chǎng)變化近似為恒定值時(shí)才會(huì)出現(xiàn)?SM值與磁場(chǎng)μ0H的線性相關(guān)性.圖5(a)和圖5(b)對(duì)比給出了LaFe11.7Si1.3和Mn0.6Fe0.4NiSi0.5Ge0.5在不同磁場(chǎng)下的熱磁曲線.可以看出,兩個(gè)樣品都在居里溫度TC附近發(fā)生了鐵磁-順磁相變.

圖4 (a)Ni50Mn34Co2Sn14和(b)LaFe11.7Si1.3的?SM值與磁場(chǎng)μ0H的依賴(lài)關(guān)系Fig.4.The magnetic f i eld dependences of?SMat peak for(a)Ni50Mn34Co2Sn14and(b)LaFe11.7Si1.3compounds,respectively.

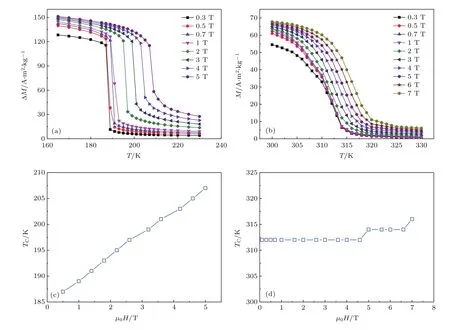
圖5 (a)LaFe11.7Si1.3和(b)Mn0.6Fe0.4NiSi0.5Ge0.5在不同磁場(chǎng)下的熱磁曲線;(c)LaFe11.7Si1.3和(d)Mn0.6Fe0.4 NiSi0.5Ge0.5的TC隨磁場(chǎng)的變化關(guān)系Fig.5. Temperature dependences of magnetization in various magnetic f i elds for(a)LaFe11.7Si1.3and(b)Mn0.6Fe0.4NiSi0.5Ge0.5;magnetic f i eld dependence of TCfor(c)LaFe11.7Si1.3and(d)Mn0.6Fe0.4NiSi0.5Ge0.5,respectively.

居里溫度TC是由dM/dT-T曲線的極小值所確定.圖5(c)和圖5(d)對(duì)比給出了LaFe11.7Si1.3和Mn0.6Fe0.4NiSi0.5Ge0.5的TC隨磁場(chǎng)的變化關(guān)系.可以看出二者的區(qū)別在于,LaFe11.7Si1.3的TC隨磁場(chǎng)增加顯著向高溫移動(dòng),導(dǎo)致T1和T2間的?M隨磁場(chǎng)變化而大幅變化,從而不具備線性相關(guān)性.相反,Mn0.6Fe0.4NiSi0.5Ge0.5的TC很難被磁場(chǎng)驅(qū)動(dòng),從而?M不隨磁場(chǎng)明顯變化,因此滿足(6)式的條件,出現(xiàn)?SM值與磁場(chǎng)μ0H的線性相關(guān)性.類(lèi)似地,Ni50Mn34Co2Sn14也同樣具有TC難以被磁場(chǎng)驅(qū)動(dòng)的情況.基于以上分析,表明當(dāng)磁結(jié)構(gòu)相變的轉(zhuǎn)變溫度具有弱磁場(chǎng)依賴(lài)性時(shí),?SM值與磁場(chǎng)μ0H表現(xiàn)出線性相關(guān)性.

4 結(jié) 論

我們發(fā)現(xiàn)一級(jí)磁結(jié)構(gòu)相變Mn0.6Fe0.4NiSi0.5Ge0.5材料的?SM值與磁場(chǎng)μ0H在高磁場(chǎng)時(shí)具有線性相關(guān)性,而在低場(chǎng)下出現(xiàn)偏差.通過(guò)麥克斯韋關(guān)系式的數(shù)值分析詳細(xì)討論了這一線性相關(guān)性以及低場(chǎng)偏差的來(lái)源,并發(fā)現(xiàn)低磁場(chǎng)時(shí),?SM近似正比于μ0H的平方.進(jìn)一步在一級(jí)磁結(jié)構(gòu)相變Ni50Mn34Co2Sn14材料中也印證了?SM與μ0H的線性相關(guān)性,但一級(jí)磁彈相變LaFe11.7Si1.3材料不具有該線性相關(guān)性.深入分析發(fā)現(xiàn),當(dāng)磁結(jié)構(gòu)相變的轉(zhuǎn)變溫度具有弱磁場(chǎng)依賴(lài)性時(shí),?SM值與磁場(chǎng)μ0H表現(xiàn)出線性相關(guān)性.在磁場(chǎng)未達(dá)到相變飽和磁場(chǎng)以下時(shí),利用?SM與μ0H的線性相關(guān)性能夠幫助我們有效地預(yù)測(cè)高磁場(chǎng)下的?SM值,可以作為很好的實(shí)驗(yàn)預(yù)測(cè)手段.

感謝西班牙塞利維亞大學(xué)物理系的Victorino Franco教授的討論.