Pair Production in Chromoelectric Field with Back Reaction?
Mo-Ran Jia(賈默然),Feng Wan(彎峰),Chong Lv(呂沖),and Bai-Song Xie(謝柏松),2,?
1College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China
2Beijing Radiation Center,Beijing 100875,China
AbstractMassless quark pair production in SU(2)gauge chromoelectric field is investigated by solving the Wigner function with back reaction.The temporal evolution of specific field and its current are obtained self consistently.For the quark distribution function,both its time and momentum dependence are studied.In particular,some interesting phenomena are found,for example,the more abundant symmetry or/and antisymmetry characteristics,the existence of the attractive basin structure and the existence of the momentum “gap” in the quark distribution and so on.All the phenomena are associated with the quark-gluon plasma oscillation,which due to the back reaction effect.The study and analysis qualitatively about the components of the Wigner function are expected to be helpful to deepen the understanding of the QCD vacuum.
Key words:particle production in Non-Abelian gauge,covariant Wigner function in Non-Abelian gauge,Schwinger mechanism
1 Introduction
In order to understand and explain the experiment results obtained by heavy ion collisions at the Super-Proton Synchrotron(SPS)and at the Relativistic Heavy Ion Collier(RHIC),a lot of theoretical models have been developed and investigated in recent years,such as models carried out by quantum field theory for both cases of quantum electrodynamics(QED)and quantum chromodynamics(QCD),[1?7]the flux-tube models,[8?14]the perturbative QCD models,[15?18]as well as the solving scheme of the classical Boltzmann equation[19?20]and scheme of the Wigner function[21?25]and so on.However,the relevant problem of microscopic mechanisms of hadron production in heavy ion collisions is not fully understood because it is hard to deal with particles of different colors for different flavors when gauge invariance and renormalization are considered completely.
Some appropriate approximation theory are not only necessary but also very important to reveal the physical mechanisms of hadron production.The flux-tube model can give a good description on the experimental results for small transverse momentum,[8?14]meanwhile,for the treatment of large transverse momentum,the perturbative QCD may be more effective.[15?18]On the other hand,by solving the Boltzmann equation or/and by solving the Wigner function[19?25]one can easily grasp the spirit of the dynamical characteristics of produced hadrons.Recently,the worldline method is also employed for the study of hadron production.[26]Another most widely promising tool is the lattice gauge calculation as the first principle method,which has been performed in many different physical situations.[27?38]By the way the similar way has also been carried out in QED cases extensively for electron pair production.[39?42]
Among the various models or/and methods mentioned above there exist still deficiency to some extent.For example some of models can not cope with the problem of whole momentum range of produced particles,and the others have disadvantages of self consistency and so on.Therefore,in this paper,in order to improve our understanding on heavy ion collision,we revisit the important topic of quark pair production in chromoelectric field by taking account into the effect of the back reaction,we make a comparison with a situation of using an approximation field and discuss the new phenomena found in the case with the back reaction.By solving the kinetic equation of Wigner Function with the back reaction in SU(2)gauge field,we have to cope with the whole momentum region.In fact it is a difficult problem as a hard task to cope with the small transverse momentum and large transverse momentum simultaneously.Here by a reasonable simplification we are succeed to focus on finding the properties in both small and large transverse momentum cases.
With back reaction it is found that the temporal evolution of specific field and its current can be obtained self consistently.And the time and momentum dependence of the quark distribution function are also obtained numerically.Some interesting phenomena are found such as that the existence of attractive basin structure and the existence of the momentum ‘gap’in the quark distribution.More abundant symmetry or/and antisymmetry characteristics in momentum distribution exist still in the studied case with back reaction.Certainly the model studied in this paper still holds some disadvantages,however,we think that the model presented in this paper will be valuable,in particular for some specific physical situations.
The paper is organized as follows.In Sec.2,we show the QCD problem in the sense of quantum field theory(QFT)by introducing the kinetic equation of the Wigner function and the field equation.In Sec.3,we simplify the self consistent system in an SU(2)gauge,where the 4-potential has been fixed in a special direction.The current,the boundary condition,and the phenomenological distribution function are also introduced in this section.In Sec.4,we give the detailed numerical results and discuss new phenomena by comparing our results with that of non self consistent system.Finally,in Sec.5,we summarize our results and make some discussions and possible outlooks.
2 Kinetic Equation of Wigner Function
In this section we introduce the Wigner operator and derive the self consistent kinetic equation for it with thefield equation.By using the assumptions mentioned in Refs.[24–25],we give the kinetic equation of the space homogeneous Wigner function after choosing a special gauged potential.
2.1 Kinetic Equation of Wigner Operator
The covariant Wigner operator is defined as
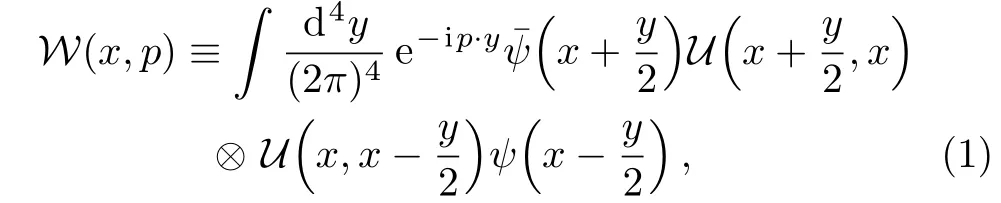
where the link operator U(β,α)is given by the path ordered exponential of a line integral,see Refs.[45–46],
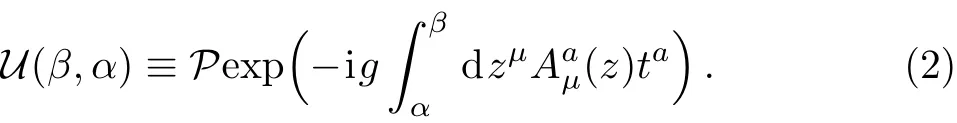
The kinetic equation of the Wigner operator can be derived from the Dirac equation wherein the colored quark obeys,
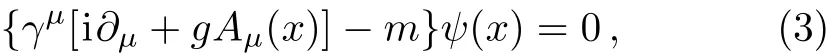
where m denotes the current mass of quark and g is the coupling constant. We choose the metric gμν=(1,?1,?1,?1)and use the natural unit~=c=1.Now we introduce the Schwinger string as that in Ref.[24].
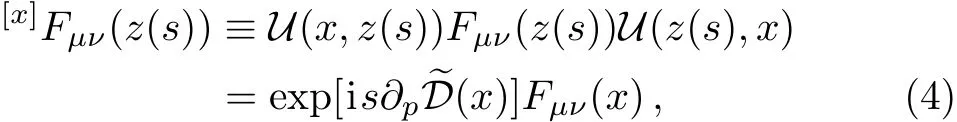
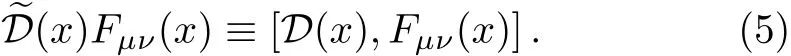
By using the properties of the link operator,we obtain the covariant transport equation for the Wigner operator of colored quark
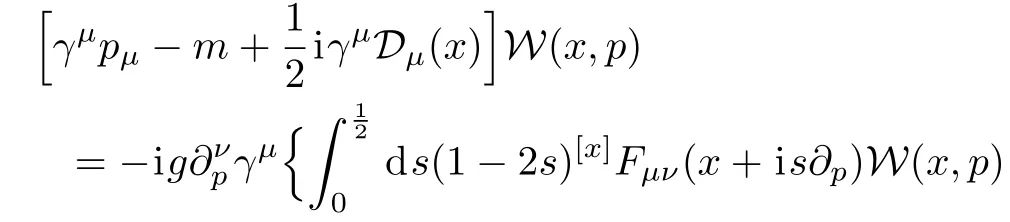
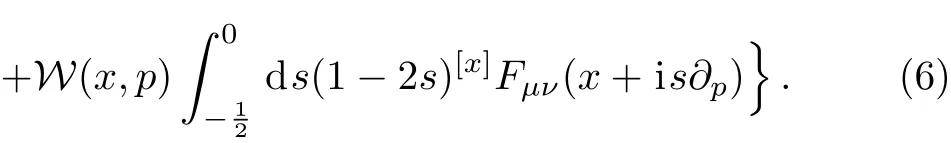
The gauged field potential is an N×N matrix in color space,which is defined by
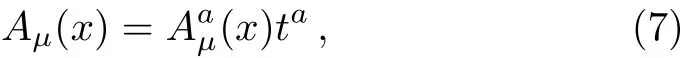
with the N2?1 hermitian generators taof SU(N)in the fundamental representation.These generators satisfy Tr(ta)=0,Tr(tatb)=(1/2)δab,and[ta,tb]=ifabctc,where fabcis the structure constant.The covariant derivative reads
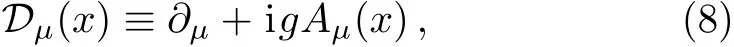
and the field strength tensor is Fμν(x) ≡[Dμ(x),Dν(x)]/(ig)which obeys the field equation
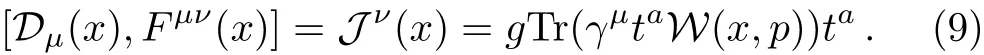
Obviously Eq.(6)and Eq.(9)are coupling with each other and constitute a self consistent dynamical system.
2.2 Kinetic Equation of Wigner Function
In order to obtain the kinetic equation of Wigner function,one can assume that the expectation value of the Wigner operator is diagonal in which gauge diagonalizes the field tensor,see Ref.[25].Also,to apply the expansion for operators,the Wigner function should be sufficiently smooth in momentum space and the field strength should vary slowly enough in coordinate space,which satisfies(?p)W·(?x)F? ~,see Ref.[24].
As a further simplification for Eq.(6),we choose a special potential,which is only in z direction and depends only on t,then the gauged 4-potential is simplified as
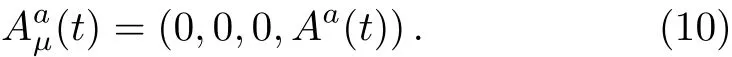
And by taking the first order approximation of the Schwinger string expansion for slow varying field,a space homogeneous Wigner function in the frame of the covariant single-time formalism is given now by
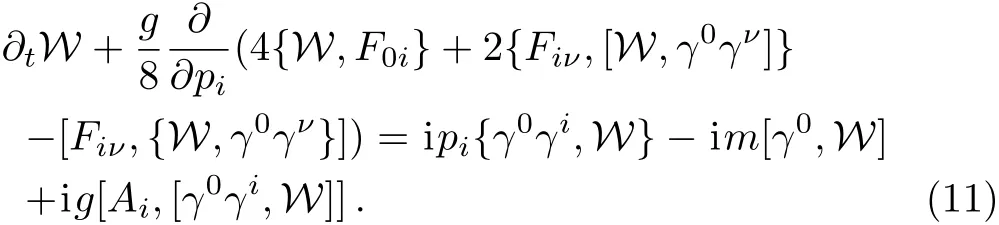
On the other hand,we have
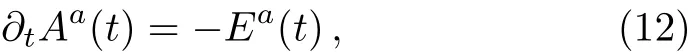
therefore,Eq.(9)can be reduced to
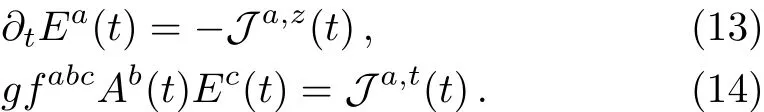
Obviously the problem becomes a Maxwell-like one.
To calculate the kinetic equation,the Wigner function can be decomposed in both color and spinor space.The color decomposition with SU(Nc)generators in fundamental representation is
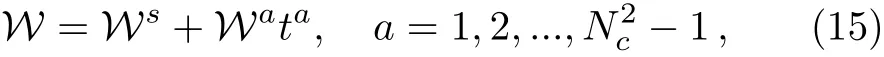
where Wsis the singlet part and Wais the multiplet part.And the spinor decomposition follows
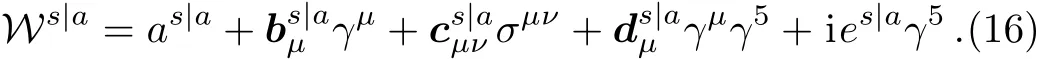
With spinor components a(scalar),b(vector),c(tensor),d(axial-vector),e(pseudo-scalar).
3 Kinetic Equations for Massless Quarks in SU(2)Gauge with Back Reaction in Fixed Color Direction
Due to the property of the SU(2)group,one can obtain general results by studying the situation of a field with fixed color direction in SU(2)case.So,in this section,we introduce the kinetic equation for massless quarks in SU(2)gauge in fixed color direction.As a study on the back reaction,we analyze the components of quark current.And we introduce the vacuum solution of Wigner function and phenomenological distribution function as a necessary for numerical study.
3.1 Kinetic Equations in SU(2)Case with Color Fixed Field
After introducing decomposition in transverse and longitudinal direction for components of Wigner function and momentum coordinate,one can substitute Eqs.(15)–(16)into Eq.(11),and obtain the components of kinetic equation for massless quarks
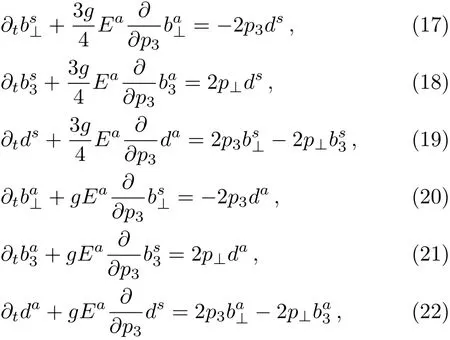
where m=0.By the way these are accordant with that in Ref.[22].
3.2 The Quark Current
In order to study the self consistent dynamical system,the quark current should be analyzed.For SU(2)case with the fixed color direction,the field equation Eq.(13)evolves while Eq.(14)is automatically satisfied.And J(t)can be written in components
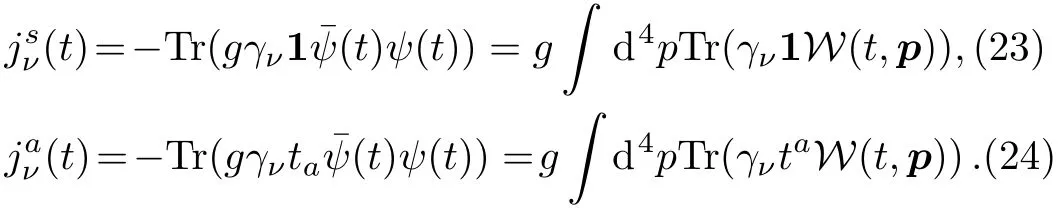
Here 1 is a 2×2 unit matrix.Since we only consider the case that the field is only in a fixed color direction,the singlet component of the current can be ignored.Substituting the Dirac matrix into Eq.(15)and Pauli matrix into Eq.(16),after performing the corresponding integral,we find that only the part of vector component bμis kept nonzero,while other parts of components a,cμν,dμ,e all vanish.Then substituting Eq.(24)into Eq.(13)we can obtain field equation reads
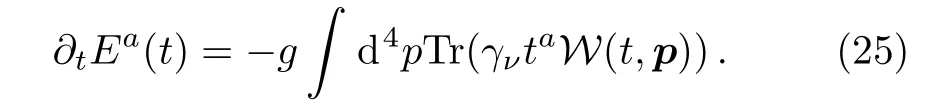
3.3 The Vaccum Solutions of the Wigner Function and the Phenomenological Distribution Function
The vacuum solution for the singlet Wigner function has the form,see Ref.[21]
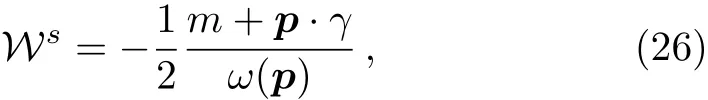
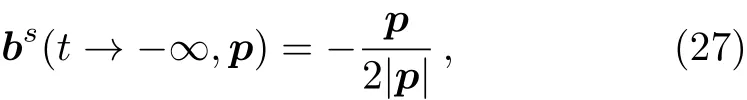
while other components of the Wigner function have zero initial values.
Via comparing the one-particle energy densitygivenbyWignerfunctionEf(t) = Tr?(m ?γipi)W(t,p)+ω(p)and by distribution function Ef(t)=4Nc
∫(d3p/(2π)3)ω(p)ff(t,p),see Refs.[21–22,24],one can obtain a phenomenological distribution function ff(t,p),
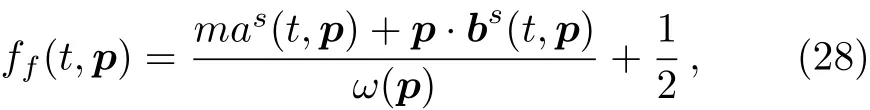
which is positive defined in a nonzero field.Here,ff=0 agrees with the vacuum solution of the Wigner function,which is physically correct.For massless particles,we can just set m=0,and obtain
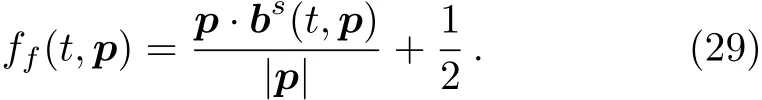
4 Numerical Results and Discussion
In this section,we give the numerical method and show the numerical results for massless quark production with back reaction.Because of the Nielsen-Olesen instability mentioned in Refs.[47–48],a static field in this model causes divergency problems,and can not give comparable results.Thus,we introduce the external Bjorken expanding field as an assumption of considering the decrease caused by the particle production.We make comparison between the Bjorken expanding case and a real back reaction case to study the quark-gluon plasma oscillation effects.
As we mentioned in Sec.1 and Sec.3,to take the back reaction into account,the integral in current Eq.(24)should be done in whole p region.But according to our calculation,the convergent region of the integral is very sensitive to the amplitude of the field E0and the coupling constant g.As the first attempt to attack this problem,the field amplitude and the coupling constant are specially chosen.In order to carry out our calculation,the trick is that we first set the coupling constant as a fixed value,then we choose an amplitude for the field,and from these two parameters find the proper cut o fffor the integration.Finally the solving of Eqs.(17)–(22)with Eqs.(12)–(13)are realized numerically.
In this paper,we set the coupling constant g=1,and choose the amplitude E0=0.34 GeV/fm,which is the half value of 0.68 GeV/fm(contact with the energy=200 AGeV in RHIC).The Bjorken expanding field reads
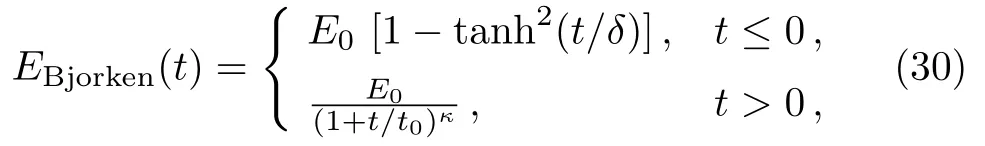
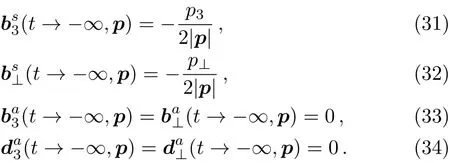
To study the massless quark production with back reaction and make a comparison with the situation in the introduced external Bjorken expanding field,we plot the evolution of the field and the current in Fig.1,the evolution of the distribution function in Fig.2,and the distribution function in momentum space in Fig.3 for the case in the Bjorken expanding field,and in Fig.4 with back reaction.
In Fig.1,we find that,when consider the real back reaction,both the field and current are damping.The field with a real back reaction decreases more slowly than that in Bjorken expanding field.The oscillations of the field and current are caused by the quark-gluon plasma oscillations due to the back reaction effects.And the damping is mitigated by the quark-gluon plasma oscillations.This indicates that when a real back reaction is involved,the typical time of the quark production is different from the case in Bjorken expanding approximation.
In Fig.2,it is found that,comparing to the case in Bjorken expanding field,yield of massless quark with real back reaction is lower at the beginning of the production,but the yield becomes higher when the time is long enough.This is because that,in a classical view,the quark-gluon plasma oscillation suppress the quark production,but as an effect of long period of time,the oscillation mitigate field from damping.And it agrees with Fig.1.The oscillation frequency of the field increases with the number of produced quarks,but when the time is long enough,such as>10,both the field and quark oscillations reach a steady state.Both the field and the produced quarks keep in an equilibrium state.The evolution property of distribution function is similar to that in U(1)with the backreaction case on that it increases first and reaches a steady state at last,see Ref.[43].
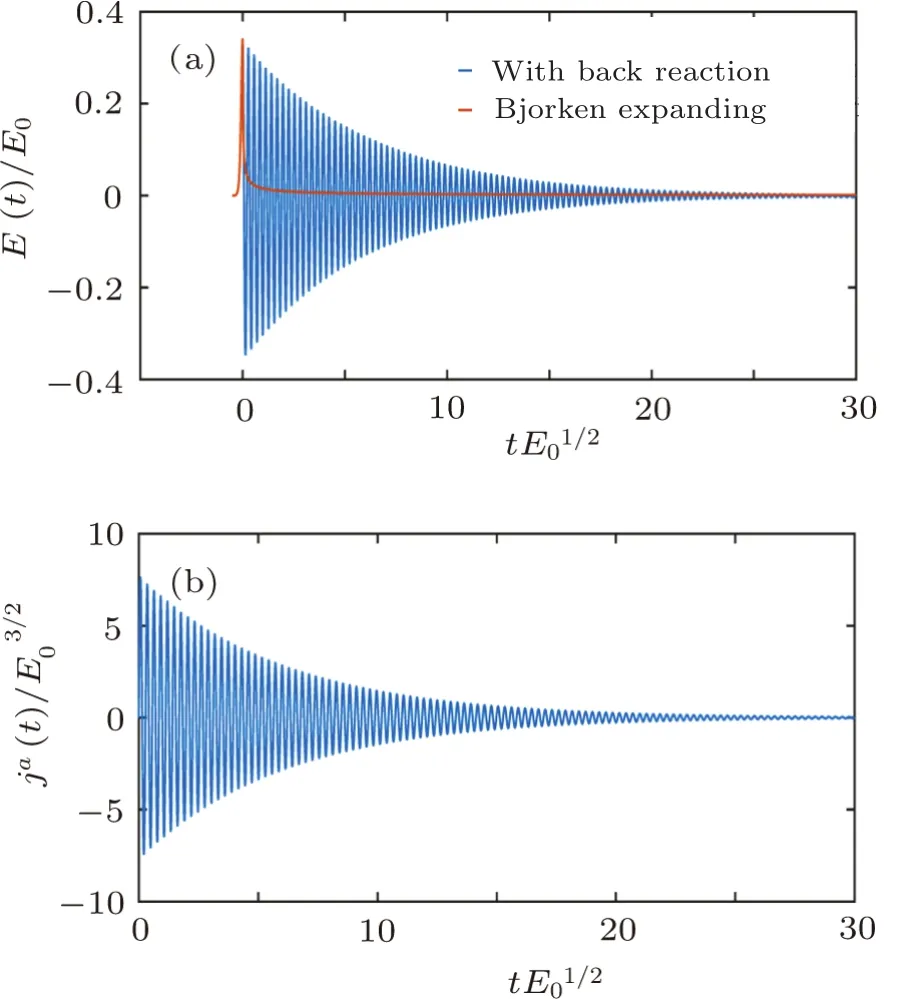
Fig.1 (Color online)Field and current as functions of t.(a)Field;(b)Current.
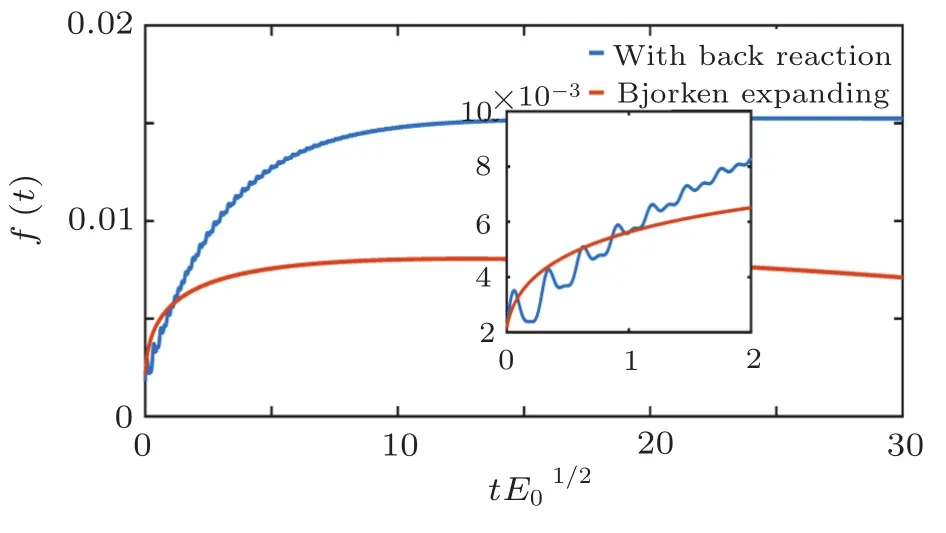
Fig.2(Color online)The phenomenological distribution as a function of f(t).
In Fig.3,in the Bjorken expanding field,the distribution function concentrates near p=0,and symmetrically distribute along p3=0.And,distribution function decreases along momentum.At different time,the momentum dependence of the distribution function holds the same form.In Fig.4,it is found that the distribution function with real back reaction has the same symmetrical properties along p3=0.However,interestingly,it is also found that a momentum gap appears,and a confinement phenomenon is formed as evolution of the distribution function in momentum space.At the beginning of the production,the distribution function has the same form as that in Fig.3.As its evolution,the distribution function shows a fluctuation variation.The production is highly distributed near p=0 and=11,and it is divided by a sector area between=12 and=16 where the production is low distributed.Thus,a confi nement phenomenon is formed.To our knowledge,thefluctuation variation of the distribution function is also due to the quark-gluon plasma oscillation.The produce quarks oscillate with the back reaction field,when time is long enough,the oscillation of both the field and produced quarks reach an equilibrium state,and confinement phenomenon is a result of this equilibrium.The slices of Fig.4 are shown in Fig.5,where the distribution function at different momentum to be shown in detail.

Fig.3 (Color online)The phenomenological distribution function in the Bjorken expanding field at different time on logarithmic scale.(a)=0.1;(b)=0.5;(c)=1.0;(d)=4.0.
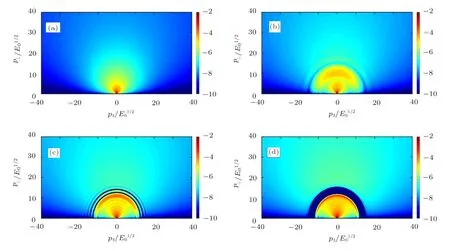
Fig.4(Color online)The phenomenological distribution function with real back reaction at different time on logarithmic scale.(a)=0.1;(b)=0.7;(c)=2.0;(d)=30.0.
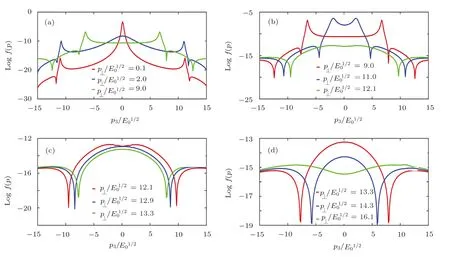
Fig.5 (Color online)Slice of Fig.4(d)with real back reaction with different momentum.
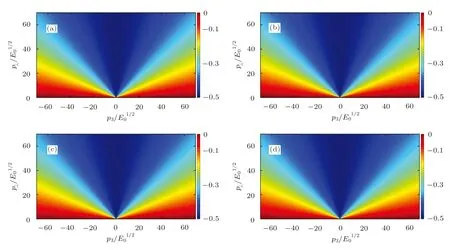
Fig.6(Color online)Vector component of Wigner functionin momentum space at different time.(a)=0.1;(b)=0.7;(c)=2.0;(d)=30.0.
In order to have a further understanding on the phenomenon so as to understand the QCD vacuum,we analyze the components of the Wigner function,and plot(p⊥,p3),(p⊥,p3),,(p⊥,p3)and(p⊥,p3)in Figs.6–9.
Since the phenomenological distribution function relates to(p⊥,p3)and(p⊥,p3)directly from Eq.(28),we plot singlet components at different times in Fig.6 and Fig.7.It is obvious that(p⊥,p3)is symmetric along p3=0 while(p⊥,p3)is antisymmetric along p3=0,which agrees with the result in Ref.[22].And the singlet components keep the same form at different times.The multiplet components relate to the current and field directly.Thus,they affect the quark production indirectly.
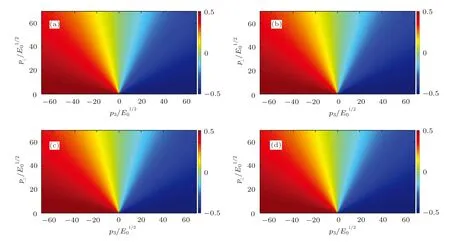
Fig.7 (Color online)Vector component of Wigner function(p⊥,p3)in momentum space at different time.(a)=0.1;(b)=0.7;(c)=2.0;(d)=30.0.
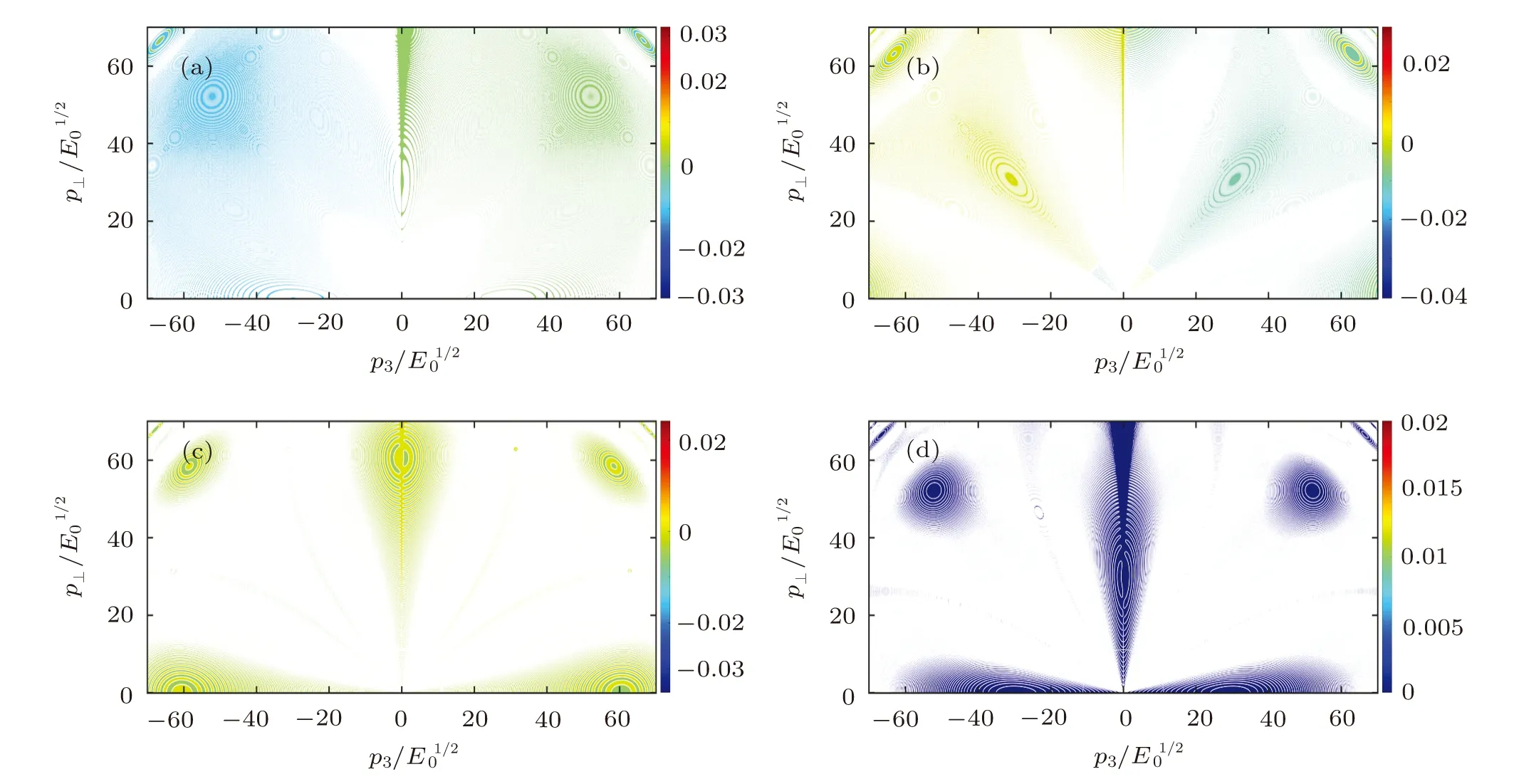
Fig.8(Color online)Vector component of Wigner function (p⊥,p3)in momentum space at different time.(a)tE01/2=15.0;(b)=20.0;(c)=25.0;(d)=30.0.
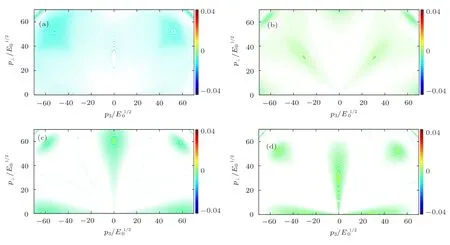
Fig.9 (Color online)Vector component of Wigner function (p⊥,p3)in momentum space at different time.(a)=15.0;(b)=20.0;(c)=25.0;(d)=30.0.
From Eqs.(17)–(22),when considering the back reaction,thefield Eaisrelated to the multiplet componentsand,and the dependence of the singlet components on the multiplet components is changed,i.e.if two functions G(,)and H(,)satisfyandand H(,)have the properties of without considering the back reaction,thus it is a possible way to avoid the integration problems.Intuitively,the momentum gap and the confinement phenomenon with attractive basin structure are due to the back reaction effects,i.e.they are caused by the equilibrium of the oscillation of both the quark-gluon plasma and the field,while the equilibrium is determined by the coupling constant g and the amplitude of the field according to our calculation.Behind these phenomena the intrinsic nonlinear dynamics mechanism plays a key role for the studied problem.
5 Conclusion and Discussion
In this paper,the massless quark production with back reaction in SU(2)gauge is studied by solving the kinetic equation of Wigner function together with the field equation.When considering the back reaction effect,both thefield and current are damping due to the plasma oscillation.Thus,as a comparison to the situation in Bjorken expanding external field,the yield of quark production is higher when the time is long enough.And the evolution of the particle production is compared with the U(1)case in Ref.[43].As a study of the distribution function in momentum space,the existent of a momentum gap is found,and the massless quark distribution forms a confinement phenomenon as the evolution.
In our opinion,these phenomena are caused by the back reaction effects due to the quark-gluon plasma oscillation.To have a further understanding on QCD vacuum,the nonvanishing components of the Wigner function are qualitatively analyzed.And the QCD vacuum structure is revealed by these nonvanishing components in this model.The symmetrical and anti-symmetrical properties of the components are conserved in comparison with the case in Bjorken expanding external field,see Ref.[22].Since the singlet components relate to the distribution function directly while the multiplet components act indirectly,in return,the produced fermions form a feedback on the field,thus the quark-gluon plasma oscillation is formed.Even though,the behaviors of strength of coupling are different in small and large momentum regions,in this paper,we choose one coupling constant and show the possibility to study a model of combining both the small and large momentum region.
We believe our calculations give reasonable results,but to have a full understanding on this problem,in our opinion,a proper function of the coupling constant g(p)is needed to be established through both experimental and theoretical methods.Once the function g(p)is obtained,further studies can be done in future.Moreover the nonlinear dynamics behind the observed phenomena can be also worthy to be explored further.
Acknowledgments
The authors would like to thank Dr.Marco Ruggieri for his helpful discussion.The computation was carried out at the HSCC of the Beijing Normal University.
 Communications in Theoretical Physics2018年10期
Communications in Theoretical Physics2018年10期
- Communications in Theoretical Physics的其它文章
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking?
- Conditional Lie-B¨acklund Symmetry and New Variable Separation Solutions of the Third Order KdV-Type Equations?
- Analytical Investigation of Soliton Solutions to Three Quantum Zakharov-Kuznetsov Equations
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations?
- Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
- Baryogenesis in f(R,T)Gravity?
