Wencai Sun·Zichun Yang·Guobing Chen

Abstract In small-sample problems, determining and controlling the errors of ordinary rigid convex set models are difficult. Therefore, a new uncertainty model called the fuzzy convex set (FCS) model is built and investigated in detail. An approach was developed to analyze the fuzzy properties of the structural eigenvalues with FCS constraints.Through this method,the approximate possibility distribution of the structural eigenvalue can be obtained.Furthermore,based on the symmetric F-programming theory,the conditional maximum and minimum values for the structural eigenvalue are presented,which can serve as nonfuzzy quantitative indicators for fuzzy problems.A practical application is provided to demonstrate the practicability and effectiveness of the proposed methods.

Keywords Structural eigenvalue·Fuzzy·Convex set·Conditional extreme·Symmetric F-programming

1 Introduction

The finite element method(FEM)has been widely applied in various fields of engineering and science,such as solid/ fluid mechanics,heat transfer, electromagnetics, and acoustics[1].The traditional FEM s are based on deterministic model,which can be called deterministic FEM s.However,in recent years,people have realized that many uncertain factors(e.g.,environmental loads,material parameters,geometries,and boundary conditions)exist in practical structures.Consequently,some non-deterministic FEMs have been developed.The probabilistic FEM(PFEM),which is based on the probability distribution of the input parameters[2–6]was first developed.However,in many cases,because of limited statistical information,obtaining an accurate probability density function(PDF)is difficult.Therefore,the PFEM suffers from many limitations in practical applications.Elishakoff[7]implemented a universal survey and systematically summarized the limitations of the probabilistic methods in engineering problems.

Recently,a number of non-probabilistic approaches for non-deterministic analysis have emerged[8].The fuzzy FEM(FFEM)has been studied by many researchers[9–11].FFEM is based on the possibility distribution of imprecise parameters,and the foundation is the subjective statistical data.In many cases,we cannot obtain sufficient statistical data from an objective test due to high cost and a long test cycle,but we can always obtain the possibility distribution function through careful planning.Thus,we can say that the fuzzy theory is an effective tool suitable for small-sample problems.

As another non-probabilistic FEM,the interval FEM(IFEM),which is based on the interval concept to describe the non-deterministic model properties,has been studied on an academic level not only for static analysis[12–19],but also dynamic analysis[20,21]and reliability optimization problems[22–24].Furthermore,Yang and Sun[25]investigated the set-based eigenvalue problem using the Kriging model and particles warm optimization(PSO)algorithm.The IFEM and FFEM are not independent,and realization of the FFEM is based on the interval cut set of fuzzy parameters.

However,when the uncertainties of the imprecise parameters are described by convex set models such as the interval(hyper-cuboid),hyper-ellipsoid,Minkowski norm convex set,cumulative energy convex set,and multiple convex set models,their exact boundaries can hardly be determined because of limited statistical information.Therefore,for problems with scarce statistical data,the ordinary rigid convex set may cause an unexpected error.

In addition,existing research works about the FFEM mainly focus on the fuzzy properties or the possibility distributions of the structural responses.However,the fuzzy property or the possibility distribution cannot definitely reflect the rough scope of the structural response,and have weak comparability.Thus,they have significant limitations in engineering application.

In the current study,the general convex set models are extended,and their boundaries are considered as fuzzy zones.Thus,a novel uncertainty model named fuzzy convex set(FCS)is presented.Then,the structural eigenvalue analysis methods based on FCS are investigated.The fuzzy properties and the definite indicators(conditional extremes)of the structural eigenvalues are studied and presented.The remainder of this paper is organized as follows.The FCS model is defined and its properties are investigated in Sect.2.Several typical FCS models are built in Sect.3.Section 4 presents a method for analysis of the fuzzy properties of the structural eigenvalues.In Sect.5,a non-fuzzy indicator,i.e.,the conditional extremes of the fuzzy eigenvalues,is presented,and two equivalent methods are provided.In Sect.6,several practical applications are provided to demonstrate the practicability and feasibility of the proposed methods.In Sect.7,some discussions are listed.In Sect.8,we complete this paper with some concluding remarks.

2 FCS models

According to fuzzy mathematics, membership function is the quantification of the compatibility of elements and a concept,or it represents the possibility that a certain element is F. For example, the possibility or the compatibility degree that Hans eats five eggs for breakfast is 0.8, but the probability is almost zero[26].In general,the probability and possibility have the following relationship[27]:

In fact,probability and possibility are two uncertainty methods with different mathematical ideas.When obtaining the PDF is difficult,we can express the parameter uncertainty from the point of view of possibility. Equation(1)shows that the uncertainty measure of the possibility tends to be larger than that of the probability.Therefore,in engineering problems,when we cannot obtain accurate PDF,we can conservatively or safely apply the possibility distribution.

From the statistical cost perspective,although the possibility and probability distribution functions are all based on statistical data,the costs contain differences.The basis of the PDF is objective test data,and that of the possibility distribution function is subjective statistical data,which can be obtained using expert scoring or questionnaire.Therefore,generally speaking,the cost of the possibility statistics is lower than that of the probability statistics.In many cases,we cannot obtain sufficient statistical data from the objective test because of the limitations in terms of high cost and long test cycle,but can always obtain the possibility distribution function through careful planning.Thus,we can say that the fuzzy theory is another tool suitable for small sample-size problem,in addition to the convex set theory.

In the following,the FCS model will be defined,and as its basis,the convex F-set and convex set are first introduced.

2.1 Convex F-set

Definition 1We assume that C is a set in n-dimensional real space,i.e.,C?Rn.If the relationship(1?t)x+t y∈C is always true as long as x,y∈C and t∈[0,1],C is a convex set.

Definition 2We assume that R represents the real number if eld,F(R)represents all the fuzzy sets in R andis one of them,i.e.,.If Eq.(2)is always true as long as x1,x2,x3∈R and x1＞x2＞x3,? is a convex F-set.

According to Definition 2,we can obtain the following corollary:

Corollary1The cut sets of convex F-set must be intervals;a fuzzy set with any cut set is an interval must be a convex fuzzy set.

2.2 FCS model

In this subsection,the FCS will be defined,and some properties will be proven.

Definition 3Let us assume thatis a formal fuzzy set in Rnand the membership function ofisIf Eq.(3)is always true as long as x,y∈Rn,t∈(0,1)and z=is called an FCS model.

According to Definition 3,we can obtain the following corollary:

Corollary2(1)The cut sets of an FCS must be convex sets.(2)A normal fuzzy set with any one cut set is a convex set must be an FCS.

Proof for Corollary 2

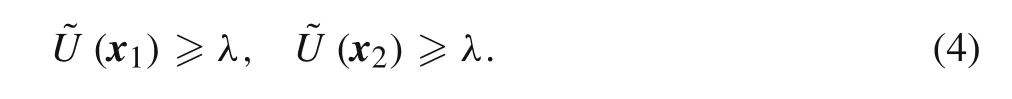
According to Definition 3,Eq.(5)is always true as long as t∈(0,1)and x3=(1?t)x1+t x2.

Therefore,x3∈Uλ,and Uλis a convex set model.

(2)In contrast,we assume thatis a normal fuzzy set in the domain Rn.?x1,x2∈Rn,andThe following relationship can be obtained:

Let us assume that t∈(0,1)and x3=(1?t)x1+t x2.Because Uλis a convex set,x3∈ Uλ.The following relationship can then be obtained:

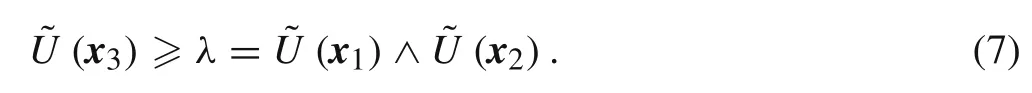
Combined with the condition that ? is a formal fuzzy set,we can learn that? is an FCS according to Definition 1.The proof ends here.

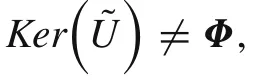
3 Typical FCS models

In practice,people often choose the convex set models,which contain analytical expressions and are convenient to use.In the following,several FCS models will be built by introducing a new parameter—the fuzzy extending parameter—into some typical convex set models[28,29].

(1)Interval FCS model:

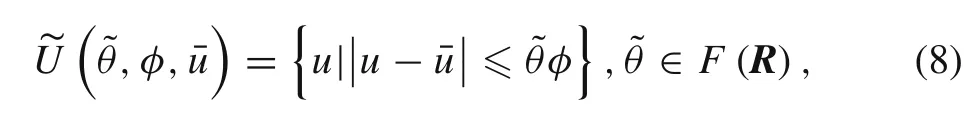
where φ is the deviation of the interval—the kernel of the FCS—andis the fuzzy extending parameter.

(2)N-dimensional ellipsoidal FCS model:

where W is a real symmetric positive definite matrix.(3)Minkowski norm FCS model:

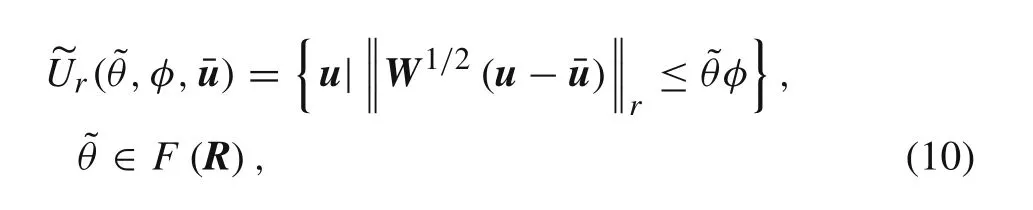
(4)FCS model for cumulative energy:

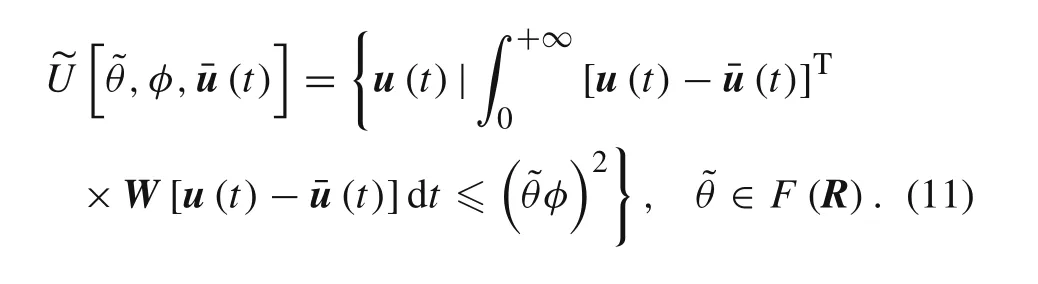
(5)FCS model for slope tolerance:

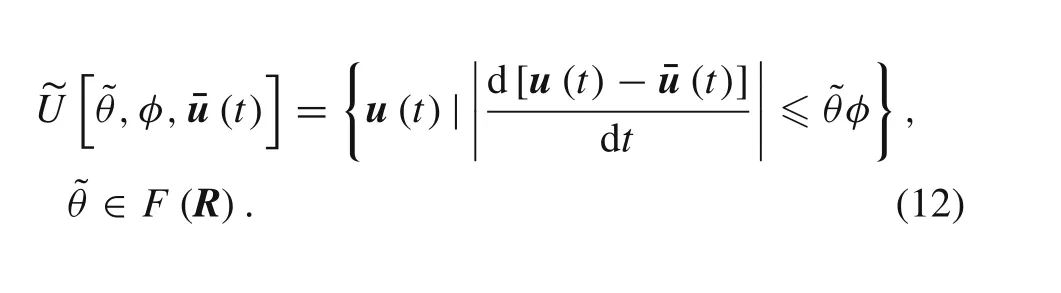
(6)Multiple FCS model:

Let us assume that non-deterministic vector x=(x1,x2,…,xn)Tcan be expressed as,where k≤n and ui(i=1,2,...,k)are sub-vectors of x.The uncertainties of the sub-vectors can be quantified by the k FCS models,i.e.,(i=1,2,...,k).The FCS model for x can be obtained as follows

where∫denotes the collection of the correspondence relationships of x and its membership grades.is the nominal value vector ofis the fuzzy vector that includes the fuzzy extending parameters.φ =(φ1,φ2,...,φk)is the scale parameter vector of the kernel of the multiple FCS model.

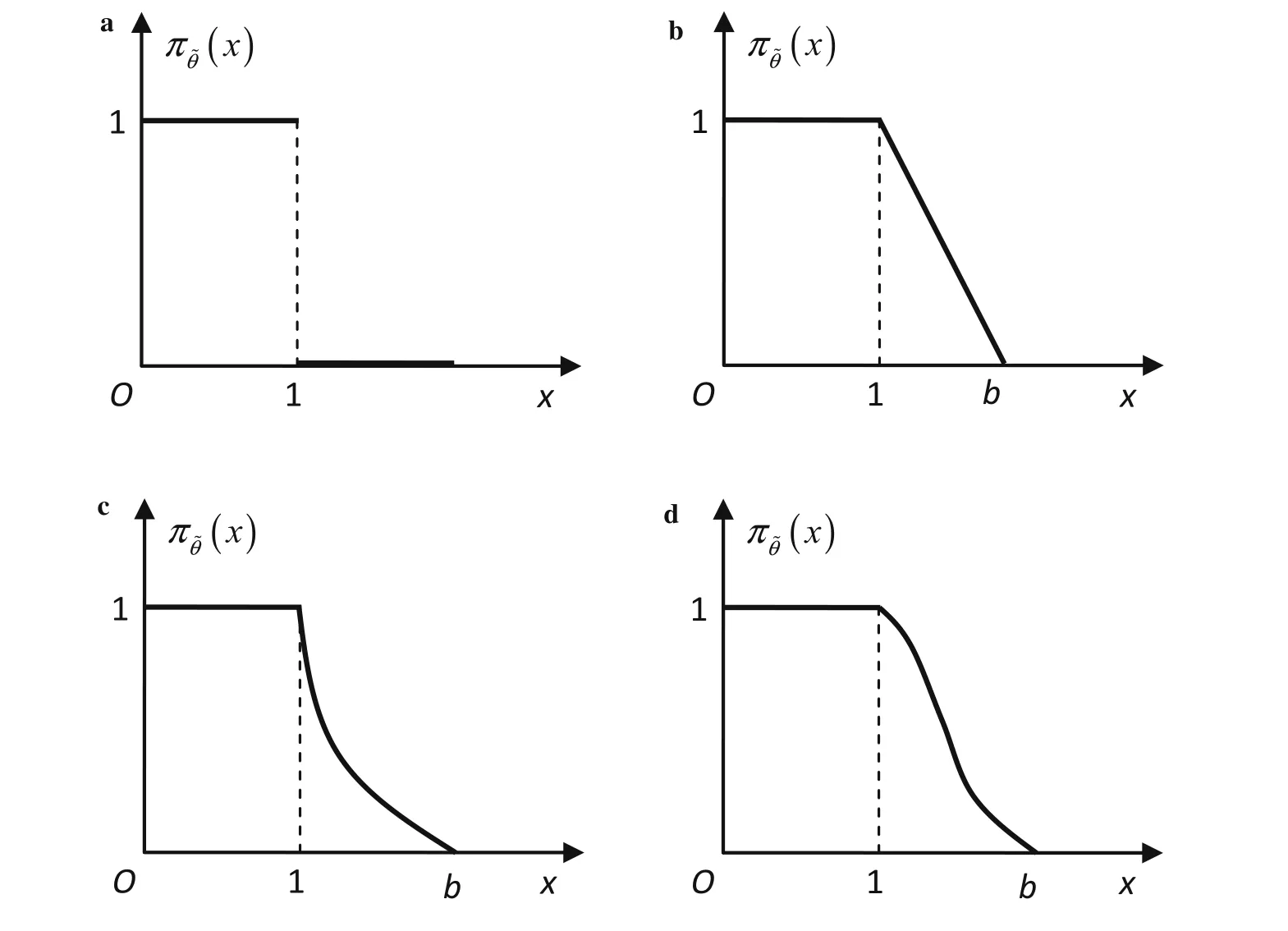
Fig.1 Typical distributions of.a Semi-rectangular distribution.b Sem i-trapezoidal distribution.c Parabolic distribution.d Normal distribution

The possibility distribution ofθ is biased to bes mall.Some typical distributions are shown in Fig.1,whereis the possibility function of the fuzzy extending parameter

4 Fuzzy properties of the structural eigenvalues

The eigenvalue problem of an undamped structure can be expressed as

We assume that the possibility distribution function of fuzzy parameteris π?i(αi).We consider some cut sets under various levels;then,a series of general interval eigenvalue problems can be obtained,i.e.,

This equation is the general eigenvalue problem with interval parameters.

The lower and upper bounds of the structural eigenvalues can form the interval vector as

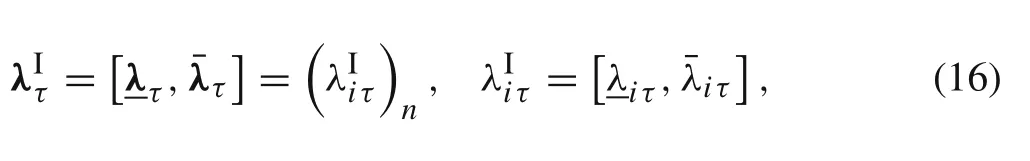
where

If the uncertainties of the structural parameters are quantified by FCS modela series of general eigenvalue problems constrained by convex set Cτcan be obtained by considering different cut-set levels.

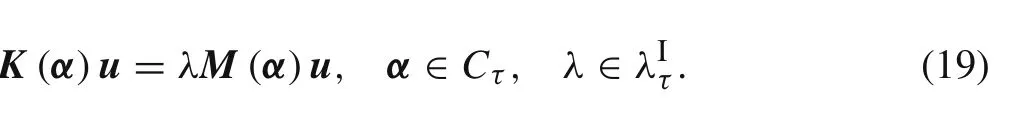
Equations(15)and(19)are the set-based finite element(SFE)problems for structural eigenvalues.

According to the decomposition theorem of the fuzzy set,the i th-order fuzzy eigenvalue can be obtained.

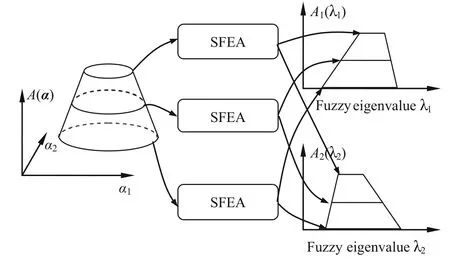
Fig.2 Procedure for analysis of the structural eigenvalue responses under FCS constraint.A(α),A1(λ1),and A2(λ2)are the possibility degree of the input parameters,output parameter λ1,and output parameter λ2,respectively.SFEA denotes the SFE analysis

In practical problems,we can choose some discrete cutset levels and analyze the corresponding intervals of the eigenvalues.The approximate possibility distribution function can be further obtained based on these intervals and corresponding cut-set levels.When the structural parameters are constrained by the FCS model, the procedure for analysis of the fuzzy properties of the structural eigenvalues is shown in Fig.2.

5 Conditional extremes for structural fuzzy eigenvalues

The possibility distributions of the structural eigenvalues can be obtained according to Sect. 4. The conditional extremes of the structural eigenvalues under fuzzy constraints are further presented in this section,which would serve as a non-fuzzy quantification indicator.

We assume that the structural eigenvalue is λ(α).When α varies in the zero-level cut set,the upper and lower bounds ofλ(α)are denoted by M and m,respectively.The following fuzzy maximum and fuzzy minimum sets can be constructed:

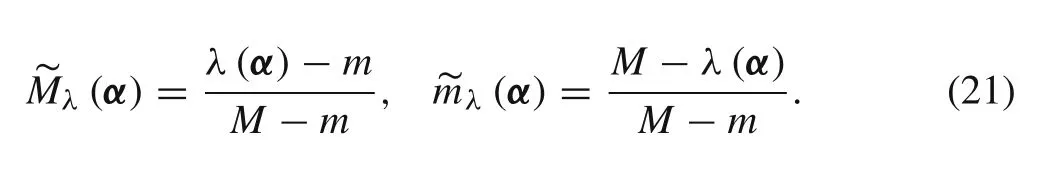
We assume that the possibility distribution of α is A(α).According to the symmetric F-programming theory[27],if existing point α?makes the following equation hold,point α?can be called the maximum element of λ(α)under the fuzzy constraint of A(α),and λ(α?)is the conditional maximum value of the structural fuzzy eigenvalue.

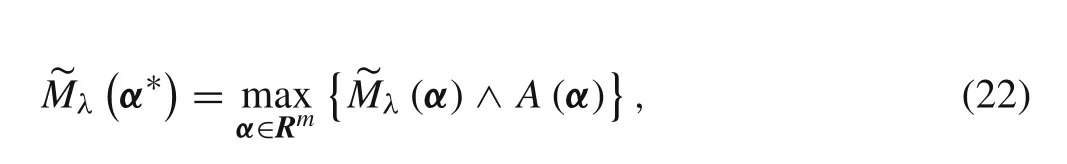
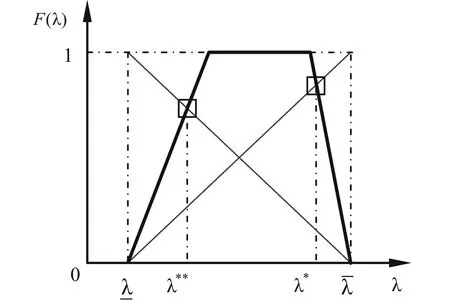
Fig.3 Solution principle of the conditional extremes under fuzzy constraint.The solid line represents the possibility distribution of the structural eigenvalue λ.The dotted lines represent the membership function of the fuzzy maximum or minimum set for λ.The dot dash lines are auxiliary lines

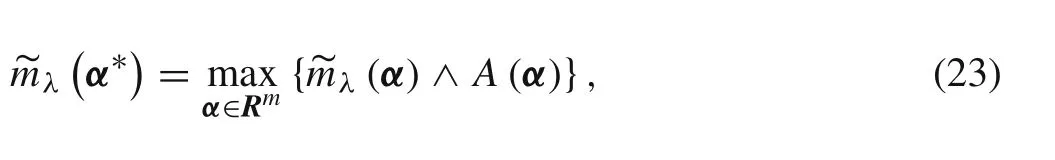
Similarly,if existing point α??makes the following equation hold,point α??is called the minimum element of λ(α)under the fuzzy constraint of A(α),and λ(α??)is the conditional minimum value of the structural eigenvalue under the constraint of A(α).

In Sect.4,the possibility distribution of the structural eigenvalue was obtained according to the fuzzy properties of the input parameters.We assume that the possibility distribution of the structural eigenvalue is F(λ)and the upper and lower bounds of the zero-level cut set of F(λ)areandrespectively.The following fuzzy maximum and fuzzy minimum sets can be constructed:

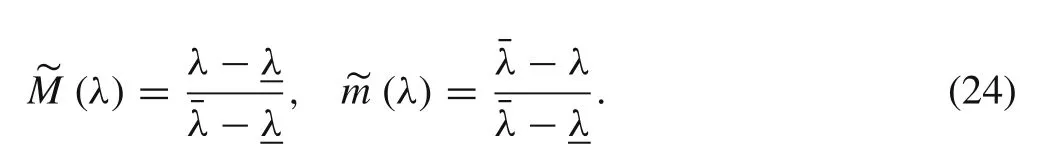
If existing point λ?makes the following equation hold

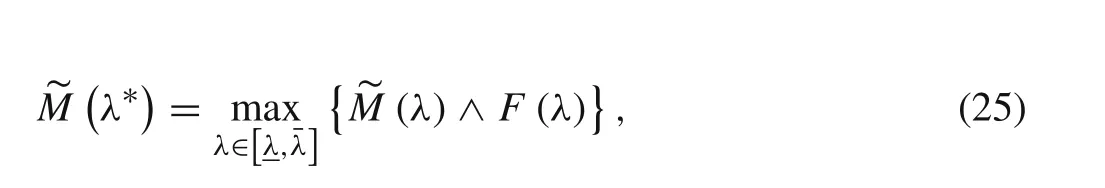
λ?is the conditional maximum value of the structural eigenvalue under the fuzzy constraint of A(α).

Fig.4 The spring mass system

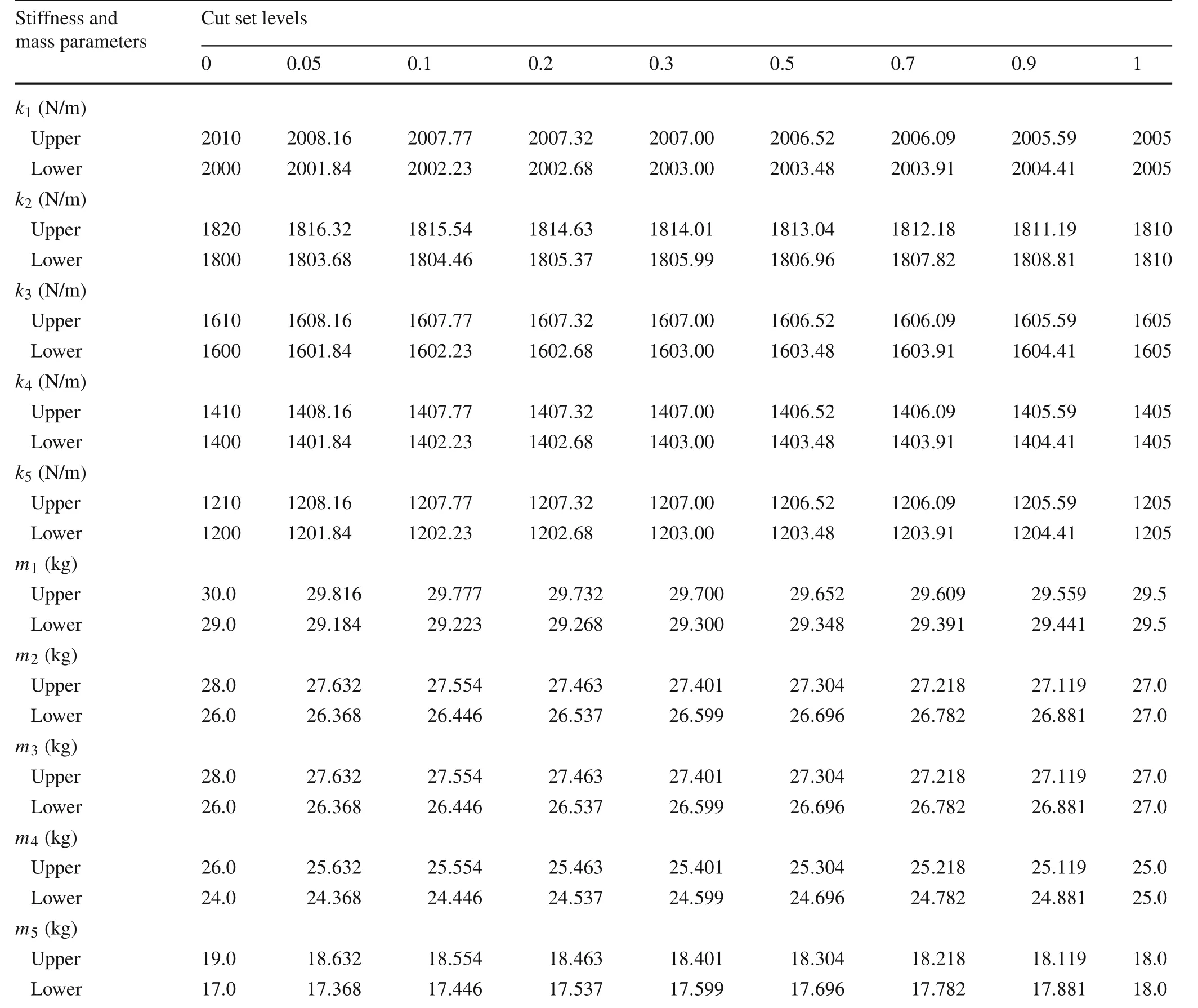
Table1 The cut sets of the physical parameters

If existing point λ??makes the following equation hold

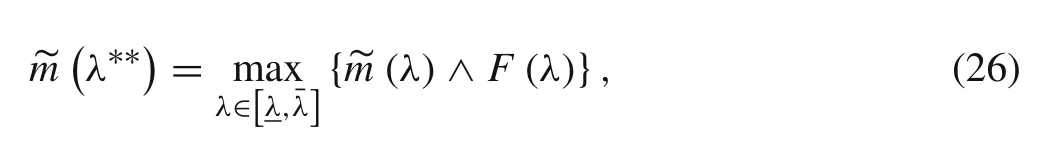
λ??is the conditional minimum value of the structural eigenvalue under the fuzzy constraint of A(α).

From this analysis,the following two relationships can be obtained:

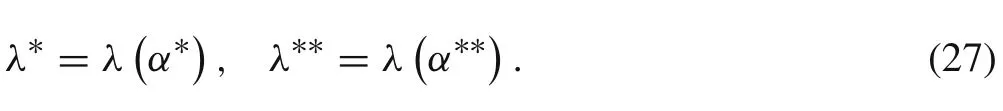
The optimization problems in Eqs.(22)and(23)or Eqs.(25)and(26)can be resolved by the PSO algorithm.

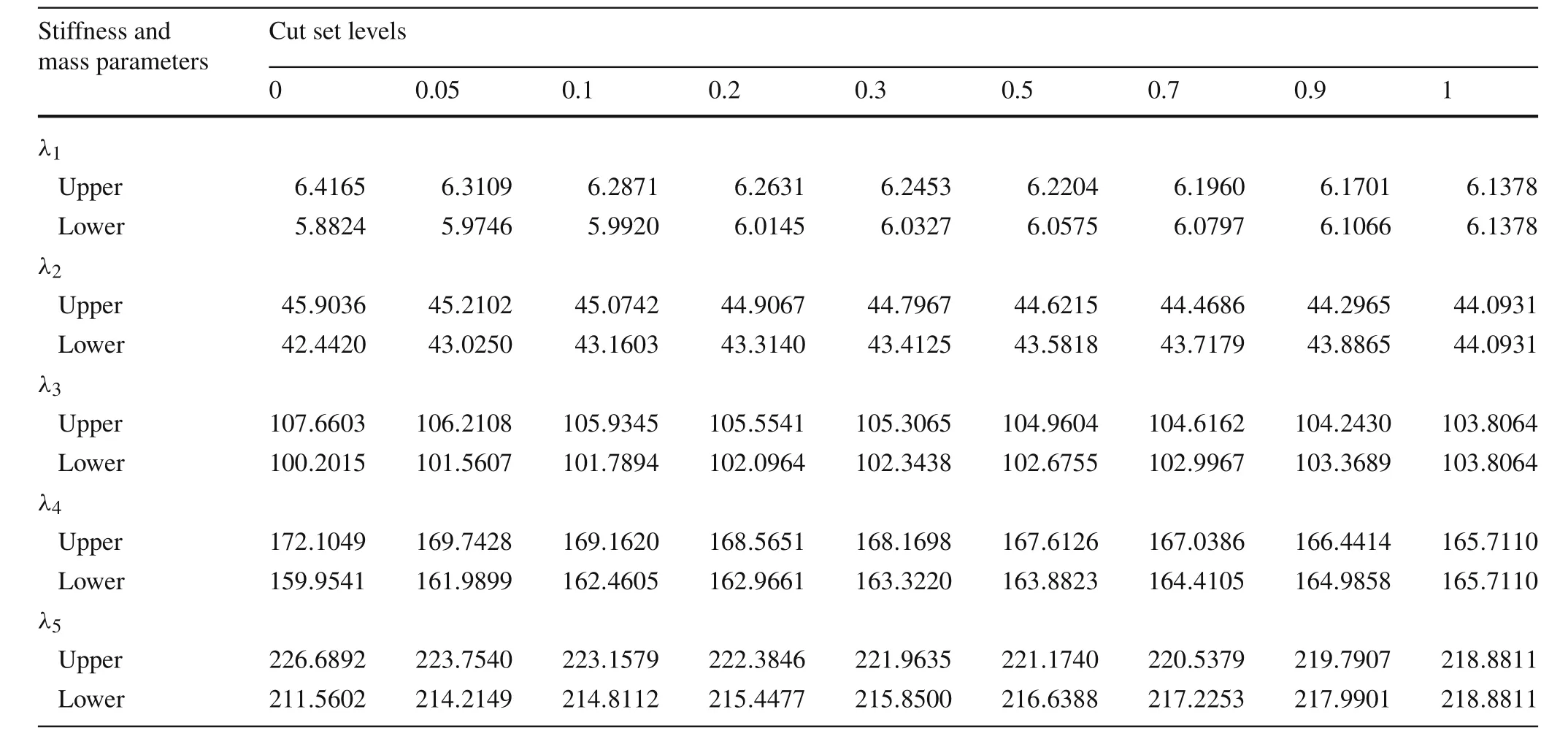
Table2 The bounds of the structural eigenvalues under the corresponding cut set levels

The solution principle of the conditional extremes of the structural eigenvalue is shown in Fig.3.

6 Numerical examples and discussion

6.1 An analytic example

Let us take the following spring mass system shown in Fig.4 as our discussion object.

The physical parameters such as the stiffness and mass parameters of this system are uncertain parameters and have fuzzy interval properties.Their possibility distributions are demonstrated as

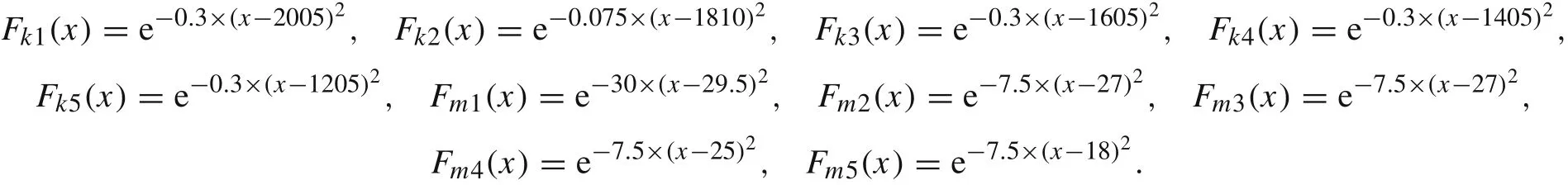
To analyze the fuzzy property of the structural eigenvalues,the physical parameters are made some cut sets as listed in Table 1.

As we know, the elements of the stiffness matrix and mass matrix are functions about the stiffness and mass parameters.The generalized eigenvalue equation of this spring mass system is

The eigenvalue equation can be abbreviated as

where K is the stiffness matrix,M is the mass matrix,X is the eigenvector and λ is structural eigenvalue.

The fuzzy properties of this system are analyzed according to the method shown in Fig.2.In order to ensure accuracy,the Monte Carlo method is applied for calculating the upper and lower bounds of every order eigenvalue.For every cut set level,the intervals values or the bounds of the structural eigenvalues are listed in Table 2.

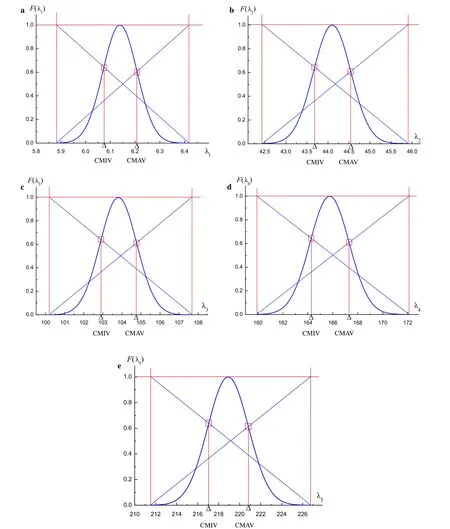
Fig.5 Possibility distributions and conditional extremes of the first-to fifth-order structural eigenvalues with fuzzy constraints.a First order.b Second order.c Third order.d Fourth order.e Fifth order

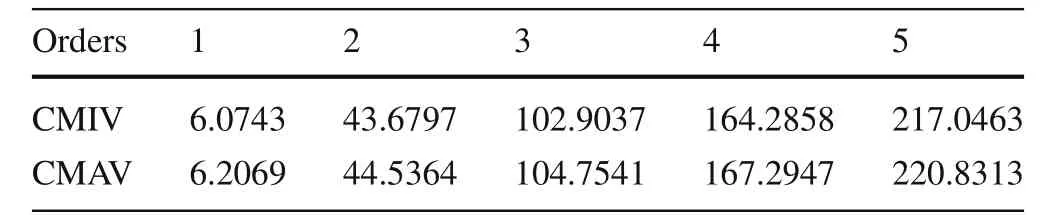
Table 3 The conditional extremes of the structural eigenvalues based on the fuzzy convex set and the symmetric F-programming theories

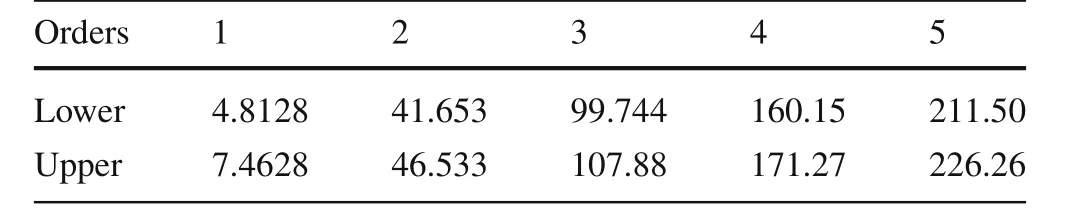
Table 4 The interval eigenvalues of the spring mass system based on the interval matrix perturbation method(Ref.[30])

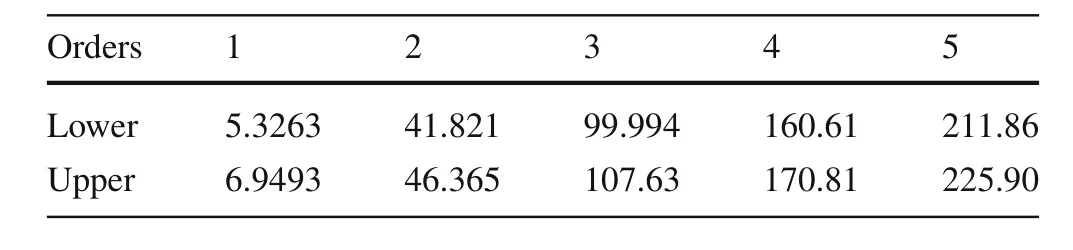
Table 5 The interval eigenvalues of the spring mass system based on the interval parameter perturbation method(Ref.[31])

The possibility or fuzzy distributions of the structural eigenvalue can be obtained based on the intervals listed in Table2according to the decomposition theorem and Eq.(20).The possibility distributions of the first-to fifth-order eigenvalues are shown in Fig.5.Then,the conditional maximum values and the conditional minimum values can be got and the results are shown in the same figure.The detail values are listed in Table 3.The interval eigenvalues based on the interval matrix perturbation method and interval parameter perturbation method are listed in Tables 4 and 5.

From this analytical example,the feasibility and scientific significance of the new methods proposed above have been verified.In addition,we can make some theoretical discussion and comparison as follows:

(1)The interval physical parameters under zero-cut set level are the same as that in Ref.[31].The interval matrix perturbation method and interval parameter perturbation method were used in that monographs to calculate the upper and lower bounds of the structural eigenvalues.However,the two methods are all low order perturbation method.They are effective only when the parameter uncertainty is small,in other word,the perturbation momentum of the stiffness and mass matrix is small.In addition,the correlation of the interval parameters is ignored in the interval matrix perturbation method.So,the accuracy of the two methods is limited.By comparison with them,the Monte Carlo method is more accurate,and the obtained results listed in Table 2 are more closed to the true values.Therefore,they lay a good foundation for obtaining the fuzzy distributions of the structural eigenvalues.

Fig.6 Geometric model of the turbine blade

Table6 Nom inal values of various parameters

(2)The conditional extremes of the eigenvalues are based on the fuzzy interval description of the physical parameters and the symmetric F-programming theory,and they are defuzzy fication indicators for the fuzzy properties of the structural dynamic characteristics.It can be found that the conditional minimum value is higher than the lower bound value by IFEM under zero-cut set level,and the conditional maximum value is lower than the upper bound value by IFEM.Therefore,if the fuzzy property of the physical parameters is ignored, the interval eigenvalues will be much wider and have no practical reference value.

(3)The whole analysis process also shows that the procedure for analyzing the fuzzy distribution of structural eigenvalues shown in Fig.2 is correct and feasible.Besides,the conditional extremes are based on the F-programming theory and application of them is very image as shown in Fig.5 or Fig.3.The accuracy of the proposed method is also verified through this analytic example which has analytic eigenvalue equation.

Fig.7 Optimization procedures for the first- and second-order natural frequencies. a Conditional maximum value of the first-order natural frequency. b Conditional minimum value of the first-order natural frequency. c Conditional maximum value of the second-order natural frequency.d Conditional minimum value of the second-order natural frequency.The symbols“ps,”“w,”and “gbest”in every figure denote the population size,inertia weight factor,and global optimum value in the PSO algorithm.The “gbest”values are the possibility degrees of the conditional extremes

6.2 An engineering example

We consider a gas-turbine blade shown in Fig.6 as an illustration example.

The nominal values of the elastic modulus,density,angular velocity,and Poisson’s ratio are listed in Table 6.

We assume that the structural parameters have fuzzy properties.Now,let us analyze the fuzzy properties and theconditional extremes of the first-to fifth-order natural frequencies of the pre-stressed turbine blade with an angular velocity.Three cases are discussed below.

Table7 Conditional extremes of the natural frequencies and the corresponding parameters

C a se 1

The uncertainties of the parameters are quantified by fuzzy intervals,i.e.,the exact boundaries of the structural parameters cannot be obtained.A fuzzy zone exists between uncertainty degrees of 4%and 5%of the nominal values.The optimization procedures for the conditional maximum and minimum values of the first-and second-order natural frequencies are shown in Fig.7.

The conditional maximum and minimum values of the first-to fifth-order natural frequencies and the corresponding parameters are listed in Table 7.

C a se 2

The uncertainties of the parameters are quantified by the following possibility distribution functions:

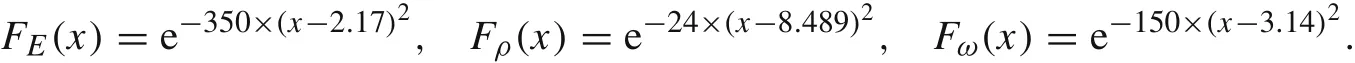
The possibility distribution and the conditional extremes of the first-to fifth-order natural frequencies are shown in Fig.8.

C a se 3

The uncertainties of the structural parameters are quantified by the FCS,i.e.,the hyper-ellipsoidal set has fuzzy boundaries.The fuzzy zone is located between the two hyperellipsoidal models with uncertainty degrees of 3%and 5%.

The conditional extremes obtained by the PSO method and the corresponding parameters are listed in Table 8.

7 Discussion

On the basis of the proposed theories,given examples,and results,some discussions can be listed as follows:

(1)The FCS model presented in this paper developed the theory of convex F-set and can meet practical engineering requirements.When an FCS is single dimensional,it is reduced to a normal convex F-set,i.e.,a fuzzy number.The FCS model can effectively overcome the limitations of the traditional rigid convex set model,e.g.,the rigid boundary is difficult to determine and the potential error is difficult to control.Therefore,FCS can better reduce the project risk.

(2)The ideas of analyzing the fuzzy properties of structural eigenvalues based on FCS model have been verified to be feasible.The further obtained conditional maximum and minimum values based on fuzzy programming theory are quantitative “defuzzification”indicators and have a significant value in engineering application.

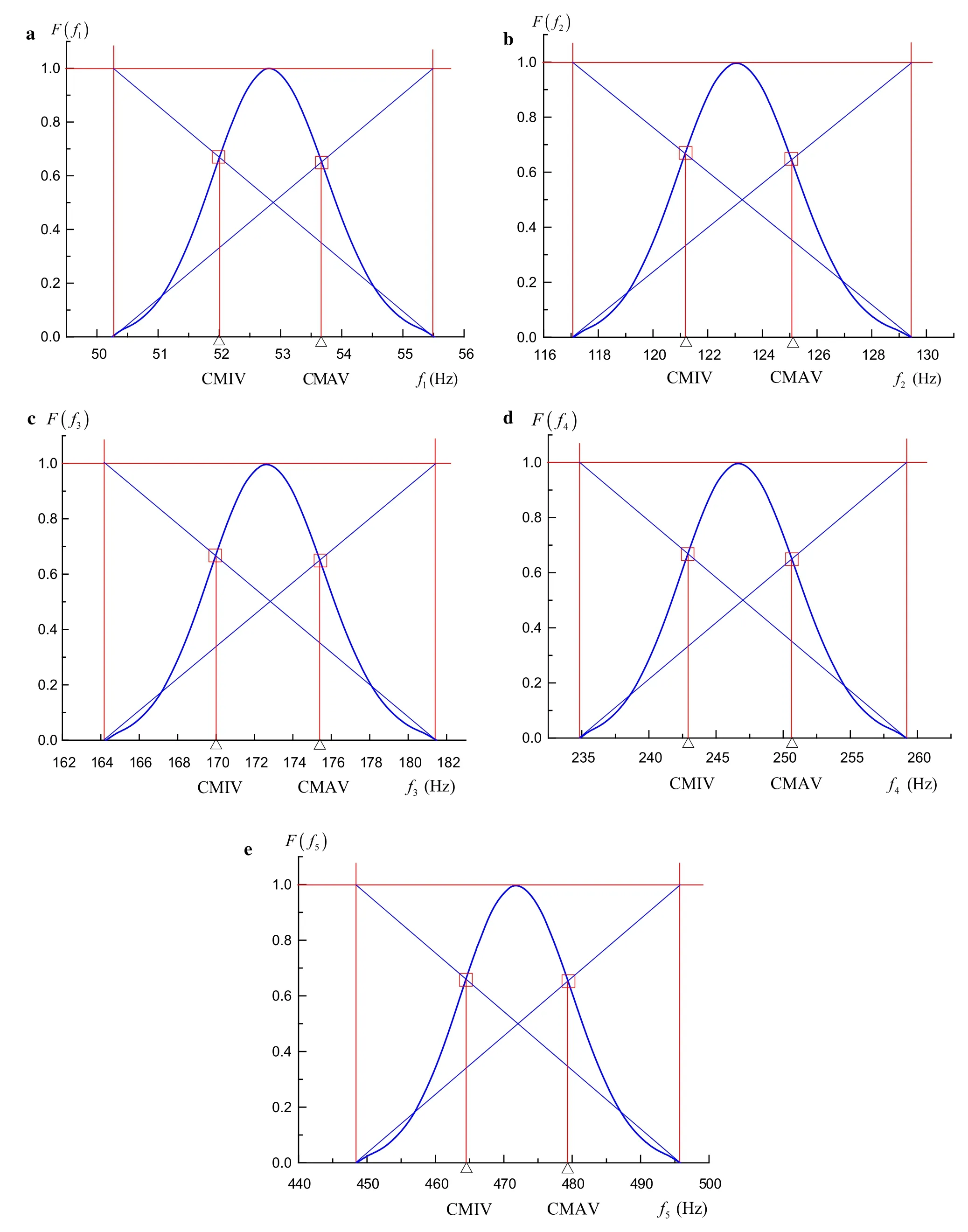
Fig.8 Possibility distributions and conditional extremes of the first-to fifth-order natural frequencies with fuzzy constraints.a First order.b Second order.c Third order.d Fourth order.e Fifth order

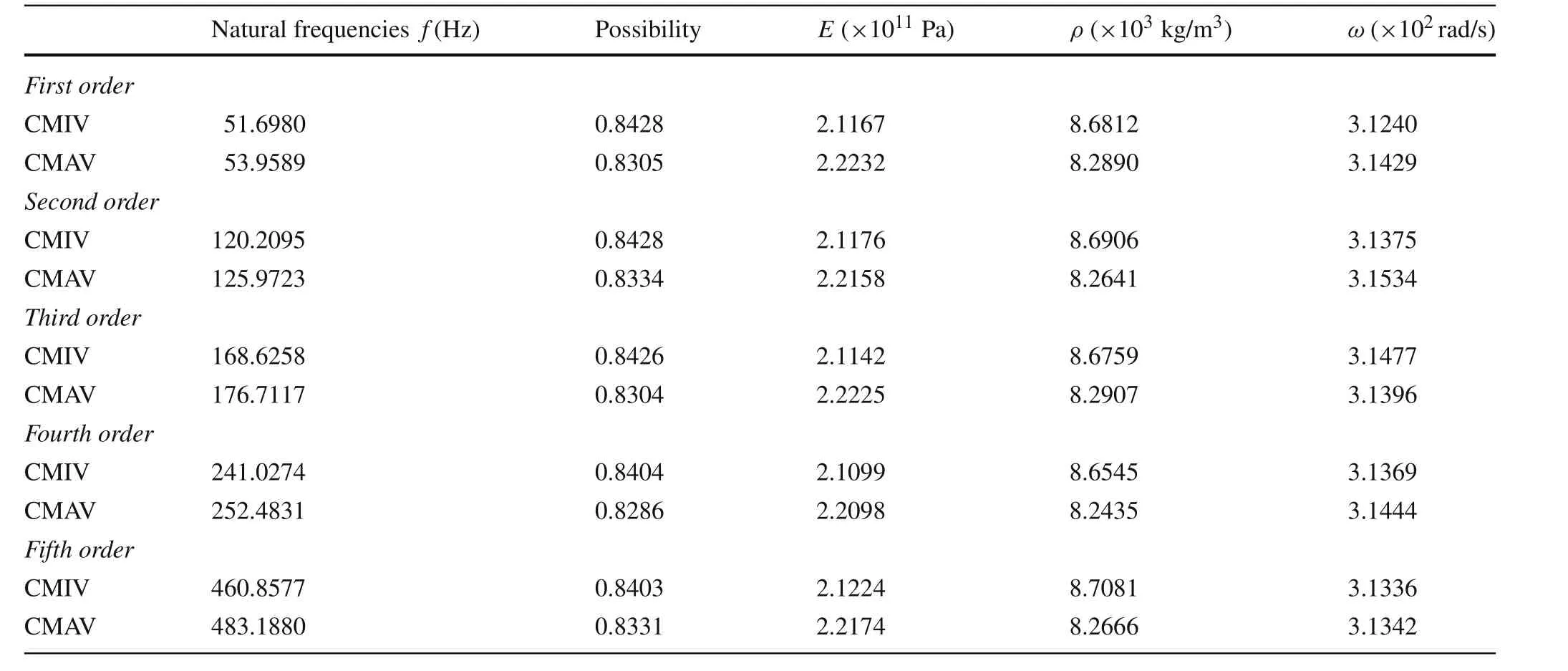
Table8 Conditional extremes of the first to fifth natural frequencies and the corresponding parameters

(3)This sample analysis shows that the presented two methods for solving the conditional extremes are all feasible and applicable in practice.If we can obtain the possibility distribution of the structural eigenvalues based on a series of cut sets of the input parameters and corresponding SFEA,the graphical solution method shown in Fig.3 is more convenient.If we construct the fuzzy maximum and minimum sets using input parameters as independent variables(i.e.,Eq.(21)),we can directly solve the optimization problems(i.e.,Eqs.(22)and(23)).In theory,the two methods are equivalent,but they have their own advantages and disadvantages.The graphical solution method can show the results in a more intuitive and concise manner but needs some SFEA times,which can reduce efficiency.In addition,an unavoidable error will occur in the drawing and reading processes.The optimization method only needs a single time of SFEA under a zero-level cut set and a single optimization time.Relatively speaking,the latter method is more efficient and accurate.However,this approach is relatively abstract in its application,and the accuracy is closely related to the optimization parameters and contains certain randomness.Generally speaking,we can choose any method depending only on the required accuracy,our habits,and even our preferences.

8 Conclusions

This paper has proposed a novel uncertainty model called the FCS model,and the problems of structural eigenvalues with fuzzy constraints are studied.The fuzzy theory(or in other words,the possibility theory)is another effective method for resolving small sample size-problems,in addition to the convex set models.A method is developed to analyze the fuzzy properties of structural eigenvalues with FCS constraint.According to the symmetric F-programming theory,the conditional maximum and minimum values of the structural eigenvalues are presented,which can serve as a non-fuzzy indicator for fuzzy eigenvalue problems.A practical application is provided,which indicates the effectiveness and practicability of the presented method.Although this study focuses on the structural eigenvalue problem,the presented methodology can be easily extended to solve other engineering problems with uncertainties,such as static response analysis,lifetime prediction,buckling,post-buckling and structural reliability.Moreover,the structural model is not limited to FEM.The method proposed in this paper can also be easily combined with the boundary element method and other novel methods such as the mesh less local Petrov–Galerkin method[32,33].These can be possible interesting study subjects in the future.

AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grant 51509254).