Electron Correlations,Spin-Orbit Coupling,and Antiferromagnetic Anisotropy in Layered Perovskite Iridates Sr2IrO4?
Hao Zhou(周浩),Yuan-Yuan Xu(徐園園),and Sen Zhou(周森),3,?1CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China
2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
3CAS Center of Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100049,China
1 Introduction
Recently,the 5d transition metal oxides Sr2IrO4has been intensively studied because it exhibits several characteristics that are considered to be distinct and important for the high-temperature superconductivity.Sr2IrO4is isostructural to the cuprate La2CuO4,sharing the layered perovskite structure of K2NiF4.[1?2]Because of the interplay between spin-orbit coupling(SOC)and electron correlations,a novel Jeff=1/2 Mott insulating ground state[3?4]was proposed for the parent compound Sr2IrO4,which becomes a canted antiferromagnetic(AFM)insulator below a Néel temperature TN230 K.Carrier doping such an insulating AFM state is expected to achieve a 5d t2g-electron analog of the 3d eg-electron hightemperature cuprate superconductors.[5?10]Although no clear signature of superconductivity has been detected so far,angle-resolved photoemission[11?13]and scanning tunneling microscopy[14]have observed in electron-doped Sr2IrO4the Fermi arcs with a pseudogap behavior and V-shaped low-energy gap.Whether a superconducting state exists as in the cuprates requires detail understanding of the correlated spin-orbit entangled insulating canted AFM states of the parent Sr2IrO4.
In the canted AFM state,the ordered in-plane magnetic moments track the θ11?staggered IrO6octahedra rotation about the z axis,[3?4,15?16]giving rise to a weak ferromagnetism(FM),which is believed to arise from the entanglement of structural distortion and SOC that introduces a strong anisotropy in the Jeff=1/2 isospin coupling.The nature of the canted AFM state in Sr2IrO4has been studied using the localized picture based on the Jeff= 1/2 pseudospin anisotropic Heisenberg model,[8,17?21]the three-orbital Hubbard model for the t2gelectrons with SOC,[22?25]and the microscopic correlated density functional theory such as the LDA+SOC+U and GGA+SOC+U.[3,26?27]Weather Sr2IrO4is an AFM Mott insulator or a Slater insulator is still under debate,[23,28?29]but it is now generally agreed that it is not deep in the Mott regime,where the localized picture is justified,since both characters have been observed experimentally.[22,30?31]This is partially the reason why the correlated density functional theory works so well in producing correctly the canted AFM as the ground state.Recent X-ray experiments[32?33]reveal that the nature of the magnetic moment deviates substantially from the ideal Jeff=1/2 picture,which cannot be accounted for by the redistribution of the orbital component within the t2gand points to the importance of egorbitals.[34]In addition,it is known that the rotation of IrO6octahedra induces a significant hybridization between the dxyof the t2gcomplex and the dx2?y2of the egcomplex.[24?26]Therefore,it is useful and desired to studythe canted AFM insulating Sr2IrO4based on microscopic model of the five 5d Ir orbitals,including both the t2gand egcomplex.
In this paper,using a five-orbital Hubbard model proposed by Zhou et al.,[35]we study the electron correlations,the SOC,and their effects on the AFM anisotropy.We apply Hartree-Fock approximation to the electron correlations to obtain the ground state properties at various electron correlations and SOC,and demonstrate their effects on the AFM anisotropy.The rest of the paper is organized as follows.In Sec.2,we introduce the fiveorbital Hubbard model constructed for the five 5d Ir orbitals,consisting of the electron hopping,crystalline electric field(CEF),the SOC,and the on-site electron correlations.The inclusion of the egorbitals enables us to resolve both the in-plane and out-of-plane anisotropy.We describe briefly the Hartree-Fock approximation and numerical calculation method used to solve the five-orbital Hubbard model.The effects of electron correlations on the AFM anisotropy is presented in Sec.3 at a constant SOC of its physical value in Sr2IrO4.In the plane of U versus J/U,the five-orbital Hubbard model exhibits a rich magnetic phase structure consisting of paramagnetic(PM)phase,coplanar canted AFM phase,and collinear AFM phase with moments pointing along the z axis(hereafter referred to as z-AFM).A Variational calculation is introduced to study the in-plane and out-of-plane anisotropy.The effects of SOC is illustrated in Sec.4 by examining the behavior of the states as a function of SOC with fixed electron correlations.Though the values of anisotropy energies depends strongly on its strength,the SOC is shown to be ineffective in tuning the direction of the ordered AFM moment.Finally,we conclude our paper in Sec.5.
2 Five-Orbital Hubbard Model
We start with the two-dimensional five-orbital tightbinding model including SOC(TB+SOC)[35]of the five localized 5d Wannier orbitals centered at Ir site labeled by μ,ν =1(dYZ),2(dZX),3(dXY),4(d3Z2?R2),5(dX2?Y2),which captures faithfully the realistic low-energy electronic structure of Sr2IrO4obtained in the local-density approximation including SOC and the structural distortion.The TB+SOC Hamiltonian in the local coordinates that rotate with the IrO6octahedra has the form of
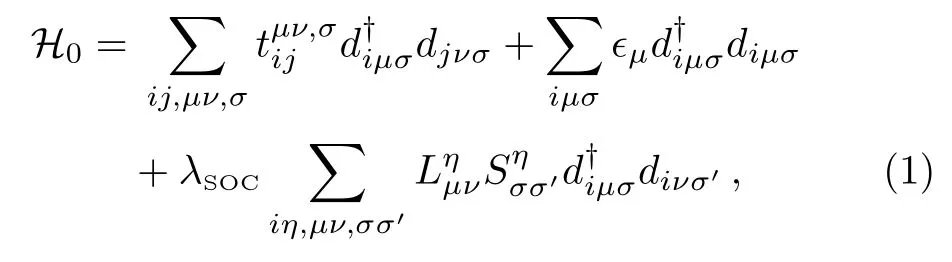
wherecreates an electron with spin-σ in the μ-th orbital at site i,andis the hopping integrals between sites i and j of up to fifth nearest neighbors given in Ref.[35].Because of the staggered IrO6octahedral rotation along the z axis,the hopping integralsare complex and spin dependent,and the Ir sites are divided into two sublattices,IrAand IrBshown in the inset of Fig.1.The second term denotes the crystalline electric field(CEF)1,...,5=(0,0,202,3054,3831)meV,which produces correctly the hierarchy of CEF in the elongated octahedra IrO6.The separation between the t2gand egcomplexes due to the octahedral ligand field is?c≡10Dq3.4 eV.The last term in Eq.(1)describes the atomic SOC with the strength λSOC=357 meV.The matrix elements of the spin angular momentum in the spin spacewhere η =x,y,z and τηthe Pauli matrices,and the matrix elements of the orbital angular moment in the five d-orbital basis=?are given explicitly in Ref.[35].
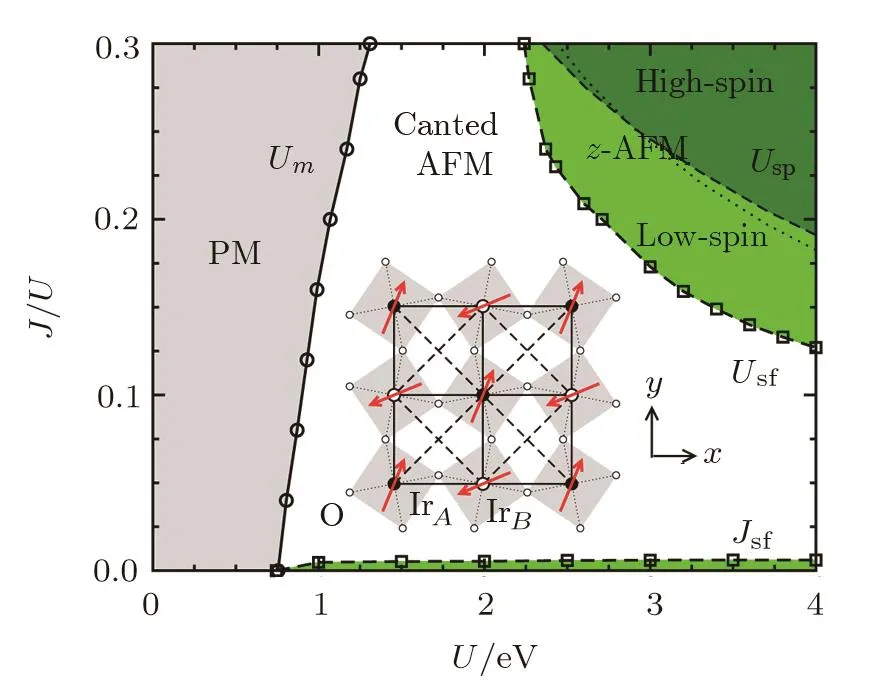
Fig.1 Magnetic phase diagram as a function of J/U and U for the five-orbital Hubbard model at n=5 with λSOC=357 meV.The grey-shaded regime corresponds to the PM phase,the green-shaded area denotes the collinear z-AFM phase,and the rest unshaded regime is for the in-plane canted AFM phase.The dashed line separating the light-green and dark-green shaded areas indicates a spin-state transition from low-spin state to high-spin state in the z-AFM phase,and the nearby dotted line corresponding to J=0.73 eV.The inset shows the schematics of the in-plane canted AFM moments on the Ir square lattice with a two-dimensional rendering of the staggered IrO6octahedral rotation.
To study the interplay between electron correlations and SOC,and their effects on the magnetic anisotropy,we consider the five-orbital Hubbard model
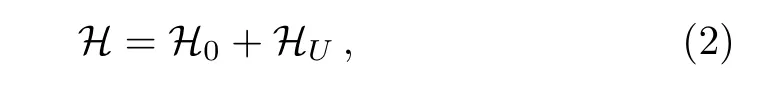
where the intra-atomic interaction HUis given by the standard multiorbital Hubbard model[36]
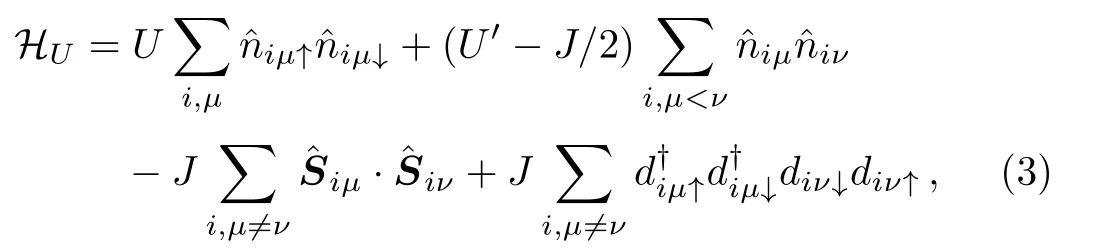
which consists of the local Coulomb repulsion U(intraorbital)and U′(interorbital),and the Hund’s rule coupling J,with the relation U=U′+2J applied.Note that,in Eq.(3)for the complete set of five d orbitals,J should be understood as an average of the exchange interactions of the t2gand the egorbitals since the difference between them is usually small in cubic systems.[37?38]To investigate the ground state properties of the five-orbital Hubbard model,the Hartree-Fock approximation will be applied to the electron correlation in Eq.(3).In the presence of SOC,the Hartree and exchange self-energies induced by HUdepend on the full spin-orbital-dependent density matrixwhich are determined by minimizing the state energy via a numerical self-consistent iterative process.Local physical quantities in the ground state can be expressed in terms ofthe orbital occupation niμ= ∑,the spin density
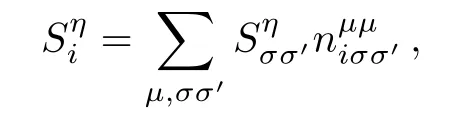
and the orbital angular momentum
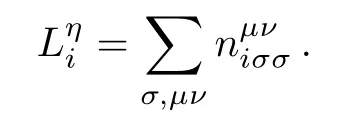
Here and after,we restrict the averaged density per site n=(1/N)∑iμniμ=5 for the undoped Sr2IrO4compound.
In this paper,we focus on the anisotropy of the correlation-induced AFM moment in the presence of SOC.We thus restrict the local density matriceson lattice sites belongs to the same sublattice(A or B)to be identical,and perform a momentum-space calculation for the two-sublattice system.The ordered spin moment on each site thus can be expressed as Si=SFM+(?1)ix+iySAFM,and the(π,π)-ordered AFM and the(0,0)-ordered FM component are given by,respectively,
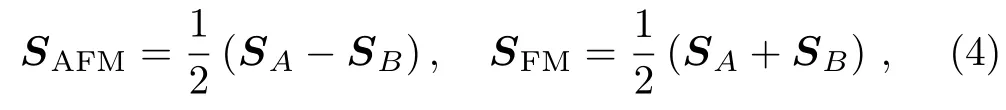
where SA/Bdenotes the expectation values of the spin angular moment on sublattice A/B.Similarly,the orbit angular moment L and the total magnetic moment L+2S can be decomposed into AFM and FM components.In all numerical calculations presented in this paper,we discretize evenly the reduced Brillouin zone,corresponding to the enlarged unit cell containing one IrAand one IrBsites,into 400×400 k points.The criteria of convergence is set so that the sum of changes of all Hartree-Fock expectation values is less than 10?6.Under this criteria,the typical number of iterations needed for convergence is about 2000.At the end,calculations with different initials may converge to different states at one set of Hamiltonian parameters,and the one with the lowest energy should be chosen as the ground state.
3 Effects of Electron Correlations
3.1 Magnetic Phase Diagram
We first fix the strength of SOC to be the physical value in Sr2IrO4,λ=357 meV,and study the effects of electron correlations,Hund’s rule coupling J and intraorbital repulsion U explicitly,on the anisotropy of the AFM moment.The main result is summarized in Fig.1,the Hartree-Fock phase diagram of the five-orbital Hubbard model shown in the plane of U versus J/U ratio,where U varying from 0 to 4 eV and J/U varying from 0 to 0.3 for the physical parameters relevant to 5d iridates.It shows clearly that,even at a constant SOC,the interplay between U and J leads to a very rich and interesting magnetic phase diagram.The phase diagram exhibits three phases,the PM,the in-plane canted AFM,and the collinear z-AFM phase.The inset shows the schematics of the canted AFM moments on the Ir square lattice with a two-dimensional rendering of the staggered IrO6octahedral rotation.In addition to an AFM component in the diagonal direction along the next-nearest-neighbor Ir-Ir bond(e.g.[1,1,0]),the ordered local moments on Ir sites in the canted AFM phase have an FM component perpendicular to the AFM component(e.g.[1,ˉ1,0]),originated from the staggered rotation of the IrO6octahedra.It is interesting to note that the critical intraorbital repulsion Umrequired for the emergence of AFM order is stronger for larger J/U ratio,in contrast to multiorbital systems without SOC.[39?41]This behavior is naturally understood since the Hund’s rule coupling competes with the SOC and works destructively for the formation of the quasiparticles of L+S character originated from SOC.[24,42]The AFM ordered phase is divided into three regimes in the phase diagram by two spin- flop transitions between the canted AFM and the z-AFM phases,Jsfin the small J/U regime beyond Um,and Usfin the regime with large J/U and large U.In the upper-right portion of the phase diagram,there is a spin-state transition from low-spin states to high-spin states in the z-AFM states.As we shall demonstrate later in this section,all phase transitions exhibited in the phase diagram are first-order.
3.2 Antiferromagnetic Anisotropy
In order to elaborate the anisotropy in the AFM ordered moment,we performed a variational calculation,which fixes the AFM moment into a specific direction.In practice,we restrict instead the direction of the AFM spin moment by adding a constraint term W(e0AFM?|SAFM|)to the Hamiltonian in Eq.(2),where e0is the unit vector along the desired direction and W is the corresponding Lagrange multiplier.Effectively,W acts as a staggered Zeeman field to pine SAFMalong the desired direction,and this term would not contribute to the state energy as long as the constraint is satisfied.Figure 2 plots the AFM state energy per Ir site as a function of the pinned direction of SAFMat six sets of electron correlations.For clarity,all energies are shown with respect to the[1,0,0]-ordered AFM state with SAFMalong the xaxis.Here and after,we use Ex,Exy,and Ezto denote the energy per site of the states with SAFMpointing along,respectively,[1,0,0],[1,1,0],and[0,0,1]direction.To describe the AFM anisotropy quantitatively,we introduce an out-of-plane anisotropy energy?Ez=Ez?Exand an in-plane anisotropy energy?Exy=Exy?Ex.
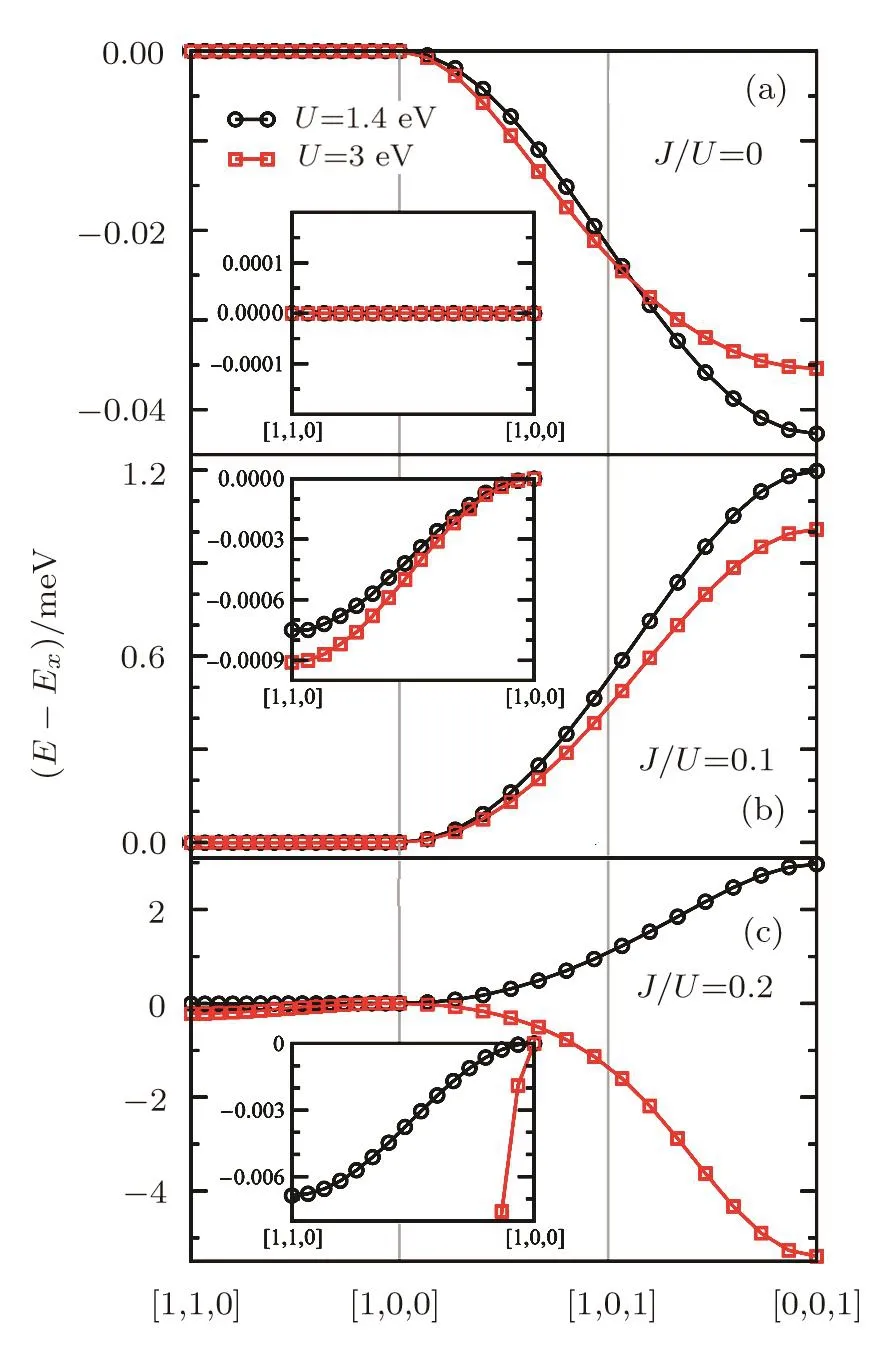
Fig.2 The state energy per site as a function of the AFM moment direction at U=1.4 eV and U=3 eV with(a)J/U=0,(b)J/U=0.1,and(c)J/U=0.2.Insets focus on the in-plane magnetic anisotropy with the AFM moment rotating within the xy-plane.
In the absence of the Hund’s rule coupling J=0,as shown in Fig.2(a)for both U=(1.4 and 3)eV,the state energy is independent of the AFM moment direction so long as it lies in the xy-plane,and it starts to decrease as the moment is tilted away from the plane,reaching a minimum at[0,0,1]direction.Quantitatively,?Exy=(0,0)and ?Ez=(?0.043,?0.035)meV at U=(1.4,3)eV,implying an easy-axis AFM along the z-axis with xy-plane rotational symmetry.The ground state is thus a z-AFM at both U=(1.4 and 3)eV.At J/U=0.1,one can see clearly from Fig.2(b)that the minimum at[0,0,1]becomes a maximum in the state energy,and a new shallow minimum is developed at[1,1,0].For U=(1.4,3)eV,the in-plane anisotropy energy?Exy=(?0.75,?0.91) μeV,and the out-of-plane anisotropy energy?Ez=(1.20,1.01)meV.It tells us that the system now prefers an easy-plane AFM moment and,in addition,the xy-plane rotational symmetry is broken into a C4symmetry,with the ground state of the lowest energy being the canted AFM along the[1,1,0]direction,giving rise to the canted AFM regime in the phase diagram shown in Fig.1.The C4symmetry of the xy-plane AFM moment is protected by the C4symmetry along principal z axis of the IrO6octahedra.When the J/U ratio reaches 0.2,the direction dependence of the state energy is pretty much unchanged at U=1.4 eV except for enlarged magnetic anisotropy with?Exy=?6.9μeV and?Ez=3.0 meV.On the other hand,its behavior is significantly different for U=3 eV.The state energy now has two minima located at[1,1,0]and[0,0,1],with?Exy=?213.4μeV and?Ez=?5.4 meV,leading to an easy-axis AFM along the z axis.
In summary,the AFM moment has the xy-plane rotational symmetry in the absence of Hund’s rule coupling J,and the inclusion of J breaks the rotational symmetry to a C4symmetry with[1,1,0]being the preferred direction for in-plane AFM moment.In contrast,the out-of-plane anisotropy of the AFM moment is nonzero even in the absence of J,and the Hund’s rule coupling J has an interesting nonmonotonic effect on the out-ofplane anisotropy,allowing a reentrance behavior of the z-AFM state. In addition,the in-plane anisotropy is much weaker than the out-of-plane anisotropy,consistent with recent experiment.[43]It is important to note that a three-orbital Hubbard model of the t2gcomplex,with an effective orbital angular moment L=1,is invariant under continuous rotation along the z-axis and,as a result,they could not resolve the in-plane anisotropy.[22?25]Current localized picture based on the Jeff=1/2 pseudospin anisotropic Heisenberg model is derived from the three-orbital Hubbard model of t2gorbitals.[17]It would be interesting to investigate the changes in the exchange couplings,anisotropic ones in particular,if the exchange Hamiltonian is obtained from the five-orbital Hubbard model for all five 5d Ir orbitals.The magnetic ground state in the studied parameter regime is either the collinear z-AFM state or the coplanar canted AFM state with AFM ordered moment pointing along the[1,1,0]direction,we hence limit our discussion in the rest of the paper to these two states.
3.3 Magnetic Moment and Phase Transitions
To gain detail information of the phase transitions and the ordered moment,we next examine the behavior of the canted AFM and z-AFM states as a function of U(or J/U)while keeping the value of J/U(or U) fixed,and compare their energies to determine the ground state.In Fig.3,we fix J/U=0.25 and scan the intraorbital repulsion U.The energy difference between z-AFM and canted AFM,Ez?Exy,is plotted in Fig.3(a)as a function of U,with the evolutions of the local moments,spin moment|2S|and the total magnetic moment|L+2S|shown in Figs.3(b)and 3(c),respectively,for these two states.At small U,the electron correlation is not strong enough to induce any magnetic moment,and hence the ground state is a PM metal.With increasing U,the canted AFM moment develops at Um=1.2 eV.The magnetic transition from PM to canted AFM is weakly first order as evidenced by the discontinuity in the energy difference between the PM(the z-AFM is not developed yet,and thus Ezactually denotes the energy of the PM phase)and the canted AFM shown in Fig.3(a).

Fig.3 (a)The intraorbital repulsion U dependence of the energy difference between the canted AFM and the z-AFM phase with fixed ratio J/U=0.25.The corresponding local spin moment|2S|and local magnetic moment|L+2S|are shown in(b)for the canted AFM phase and in(c)for the z-AFM phase.Insets in(c)show the schematics of the low-spin and high-spin states.The system undergoes a magnetic transition at Um=1.2 eV,a spin- flop transition at Usf=2.35 eV,and a spin-state transition at Usp=2.95 eV.The parameter regime is shaded with the color associated with the corresponding ground state,as used in Fig.1.
The z-AFM moment emerges subsequently at a slightly stronger electron correlation with U=1.26 eV.But it is still higher in energy than the canted AFM,so the latter remains as the ground state.Further increasing U,the energy difference Ez?Exyfirst increases a little bit and then start to decrease,crossing zero at Usf=2.35 eV where the direction of the ordered AFM moments flops from[1,1,0]to[0,0,1].At this first-order spin- flop transition,the ground state changes from the coplanar canted AFM to the collinear z-AFM.It is interesting to notice the existence of another transition inside the z-AFM phase at Usp=2.95 eV,which we referred to as a spin-state transition.At this transition,the size of ordered local spin moment jumps from ~1.5μBto~ 5μBwhile keeping its direction along the z-axis unchanged.Below Usp,the spin S and orbital L are strongly coupled to each other due to SOC,and the quasiparticles carry an L+S character.As a result,the ordered magnetic moment has significant contributions from both S and L.In contrast,the spin S and orbital L are decoupled beyond Usp,as evidenced by the negligible L contribution to the total magnetic moment,and the system is in a high-spin S=5/2 state with one electron occupying each of the five orbitals,as depicted in the inset of Fig.3(c).
The location of the spin-state transition can be roughly estimated by considering the atomic situation.Keeping the octahedral ligand field?cand ignoring the tetragonal crystal field for simplification,the energies of the low-spin S=1/2 and high-spin S=5/2 state are,respectively,E1/2=10(U?2J)and E5/2=10(U?3J)+2?c.When the difference E1/2?E5/2=2(5J??c)is larger than the SOC λSOC,i.e.J>(1/5)?c+(1/10)λSOC? 0.73 eV,the coupling between S and L is strongly suppressed and the system would rather stay in the high-spin state of pure S character.The dotted line in Fig.1 denotes J=0.73 eV and it is very close to the spin-state transition obtained for the itinerant electrons.
The behaviors of these two AFM states are shown in Fig.4 as a function of J/U ratio with fixed U=3 eV.The intraorbital Coulomb repulsion U is so large that both the canted AFM and z-AFM are lower in energy than the PM phase in the whole J/U regime we investigated from 0 to 0.3.Zooming into the small J/U regime,the inset of Fig.4(a)shows that the energy difference between z-AFM and canted AFM(Ez?Exy)is negative at J/U=0 and crosses zero at Jsf/U=0.06,giving rise to the small z-AFM region in the bottom-right of the phase diagram in Fig.1 and a first-order spin- flop transition at Jsf.Further increasing J/U,Ez?Exyincreases and reaches a maximum value near J/U=0.14 and then starts to decrease,across zero again at J/U=0.173,i.e.Usf=3 eV at J/U=0.173.This leads to an interesting reentrance behavior of the z-AFM state through a second first-order spin- flop transition.At an even larger J/U=0.246,the system again undergoes a spin-state transition in the z-AFM phase.The competition between Hund’s rule coupling J and SOC is most pronounced in the canted AFM phase,as shown in Fig.4(b),where the local moments,both|2S|and|L+2S|,decrease with increasing J at small J,contradictory to the conventional behavior of moment in multiorbital systems without SOC.[39?41]At small J regime where SOC dominant,the latter couples the spin S and orbital L and imposes an L+S character to the quasiparticles,and thus the ordered moment have significant contributions from both S and L.At J=0,the ratio|L|/|S|to 3.6 in the canted AFM and 5 in the z-AFM state,which is close to the expected value 4 for the ideal Jeff=1/2 moment of a spin-orbit Mott insulator,but cannot be accounted for by the redistribution of orbital components within the t2gorbitals.[33]With the increasing of the Hund’s rule coupling,the coupling between S and L is suppressed and the S character of the quasiparticles is enhanced.As a result,the ratio|L|/|S|decreases as increasing J,and drops to negligible values after the spin-state transition.

Fig.4 Same as Fig.3,but for the J/U ratio dependence with fixed U=3 eV.Inset in(a)zoom into the small J/U region,showing the spin- flop transition at Jsf.The system undergoes two spin- flop transitions at Jsf/U=0.06 and J/U=0.173(Usf=3 eV at this ratio),and a spinstate transition at J/U=0.246(Usp=3 eV at this ratio).
In summary,due to the subtle interplay between the two electron correlations,intraorbital repulsion U and Hund’s rule coupling J,and the competition between J and SOC,the system undergoes multiple phase transitions as one varying one of the electron correlation parameters while keeping the other fixed.As a result,it leads to a very rich and interesting magnetic phase diagram for the five-orbital Hubbard model at constant SOC shown in Fig.1.
4 Effects of Spin-Orbit Coupling
For a better understanding of the effects of SOC,in this section,we fix the values of electron correlations(U and J),and study the state evolution as a function of λSOC.The behavior is relatively simple at U=3 eV and J/U=0.25(i.e.,J=0.75 eV),as shown in Fig.5.At λSOC=0,the spin S and orbital L are completely decoupled,and the moment has an SU(2)rotation symmetry in the absence of SOC.As a result,the z-AFM and canted AFM are degenerate with Ez?Exy=0 at λSOC=0.Because of the large value of J,the system is in the high-spin state with all moment coming from spin,|L+2S|=|2S|=4.68 μB.Switching on λSOC,the SOC tends to couple electrons with different spins from different orbitals,disfavoring the high-spin state with pure S character.Therefore,as λSOCincreasing,the spin moment and the total moment decrease and,at the same time,the contribution from orbital L increases.Note that the decreasing of moments here is very gradual and continuous,implying a crossover between the high-spin state and lowspin state as one increases SOC.It is very different from the situation when we fix λSOCand vary the electron correlations(the Hund’s rule coupling J in particular)presented in last section,where the ground state undergoes a first-order spin-state transition as it leaves the high-spin state.The energy difference Ez?Exydecreases with increasing λSOC,reaches a minimum at λSOC0.57 eV,and then starts to increase.But it never crosses zero up to the largest value we investigated,0.7 eV,which is twice of its physical value in Sr2IrO4,and the z-AFM is always the ground state.Therefore,the ordered AFM moment in the ground state never change its direction from the z axis as the SOC strength varying from 0 to 0.7 eV at(U,J)=(3,0.75)eV,though the anisotropy energy depends strongly on λSOC.
In Fig.6,we scan λSOCwith fixed U=2 eV and J/U=0.1(i.e.,J=0.2 eV)where the ground state is in the canted AFM phase when the strength of SOC takes its physical value in Sr2IrO4,λSOC=357 meV.In the absence of SOC,λSOC=0,the magnetic moment has SU(2)rotation symmetry and all ordered moment comes from spin moment,|L+2S|=|2S|=1μB.The local moments in the canted AFM and z-AFM are plotted,respectively,in Figs.6(b)and 6(c).Switching on the SOC,the mixing of electrons with different spins suppresses the spin moment in both the canted AFM and z-AFM phase,but the behavior of the orbital L at a small but nonzero λSOCis quite different in these two AFM phases.In the z-AFM phase,the coupling between spin and orbit is very weak and the quasiparticles remains mostly S character,and thus the L contribution to the ordered moment is very small.On the other hand,the system in the canted AFM phase is found to be in a different state with lower energy,where the coupling between spin and orbital is already fully activated,despite at such a small λSOC.The orbital L contribution to the ordered moment is thus quite large.At the strongest SOC we studied,λSOC=0.7 eV,the ordered moment is 0.84 and 0.9μB,respectively,in the canted AFM and z-AFM phase,with a corresponding ratio|L|/|S|equal to 3.6 and 3.9,very close to the value of the ideal Jeff=1/2 moment.Reducing SOC from λSOC=0.7 eV,though the size of ordered moments changes very slowly in both AFM phases,it decreases in the canted AFM phase but increases in the z-AFM phase.Comparing the state energies of these two AFM phase,shown in Fig.6(a),one see clearly that the canted AFM is always lower in energy and thus being the ground state within the whole parameter regime of interest.
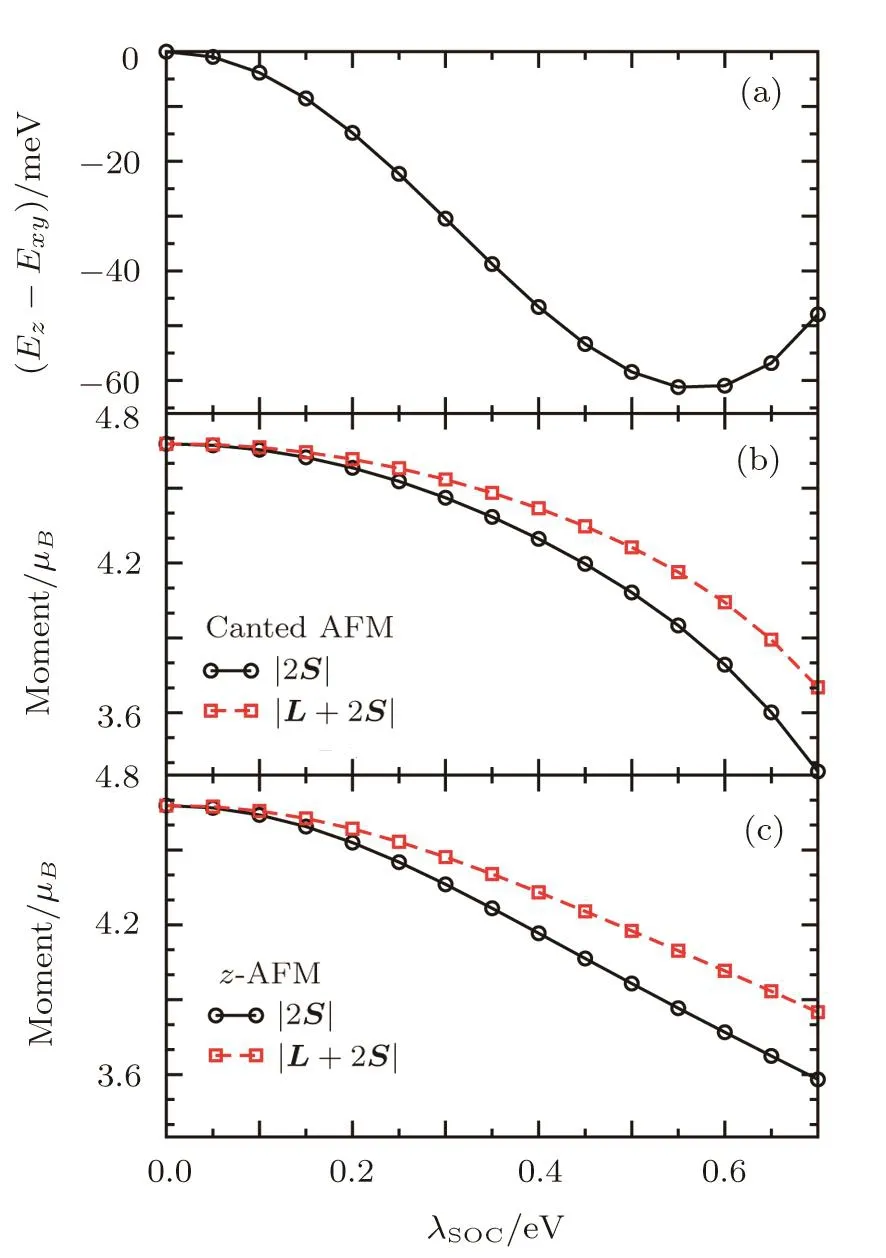
Fig.5 The λSOCdependence of the energy difference between the canted AFM and the z-AFM phase with electron correlation U=3 eV and J/U=0.25.The corresponding local spin moment|2S|and local magnetic moment|L+2S|are shown in(b)for the canted AFM phase and in(c)for the z-AFM phase.
From these two studies presented in Figs.5 and 6,we illustrate that the SOC,as the origin of magnetic anisotropy,is very ineffective in tuning the direction of the ordered AFM moment.This is very different from the situation in the strong coupling limit,[17]where the direction of the ordered AFM moment is sensitive to the strength of SOC relative to the tetragonal splitting of the t2gorbitals.
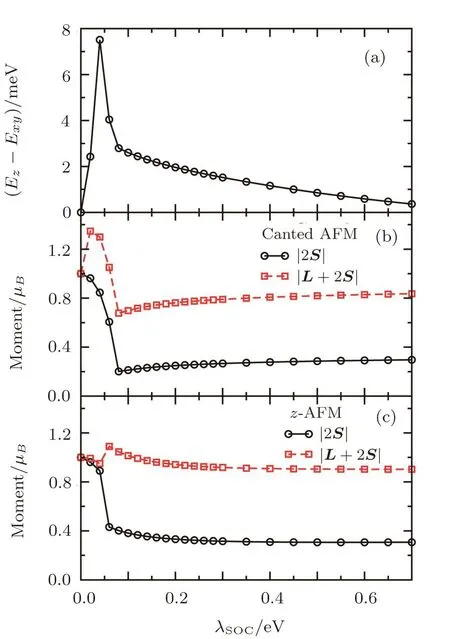
Fig.6 Same as Fig.5,but for the λSOCdependence at U=2 eV and J/U=0.1.
5 Conclusions
Based on a five-orbital Hubbard model with SOC,in which the noninteracting part describes well the realistic band structure of Sr2IrO4,we study in this paper the electron correlations,the SOC,and their effects on the AFM anisotropy.The electron correlations are treated within the Hartree-Fock approximation to obtain the ground state properties of the multi-orbital Hubbard model,at various strengths of SOC and electron correlations.We demonstrate that,at a constant SOC,the interplay between Hund’s rule coupling J and intraorbital repulsion U leads to a rich magnetic phase diagram,including a canted AFM state with weak FM moment in a large area of the phase diagram,consistent with the ground state of Sr2IrO4identified in experiments.In contrast,the SOC is shown to be very ineffective in tuning the direction of the ordered AFM moment,despite the fact that it is the origin of magnetic anisotropy.While our result cannot be considered quantitatively accurate due to the intrinsic deficiencies of mean- field approximations,our weak-coupling study is still useful in understanding qualitatively the behaviors of spin-orbit coupled multi-orbital systems.The presence of magnetic anisotropy indicates the difference between the longitudinal(out-of-plane)and transverse(in-plane)spin susceptibilities,as expected for spin-orbit entangled systems where the spin SU(2)symmetry is broken.It would be very interesting to study the effects of such difference between spin susceptibilities on the spin fluctuation mediated superconductivity,which consists of both singlet and triplet pairing due to SOC.[5,44]
Acknowledgments
We thank Kun Jiang and Hua Chen for useful discussions.
[1]G.Cao,J.Bolivar,S.McCall,et al.,Phys.Rev.B 57(1998)11039(R).
[2]M.K.Crawford,et al.,Phys.Rev.B 49 9198(1994).
[3]B.J.Kim,et al.,Phys.Rev.Lett.101(2008)076402.
[4]B.J.Kim,et al.,323(2009)1329.
[5]H.Watanabe,T.Shirakawa,and S.Yunoki,Phys.Rev.Lett.110(2013)027002.
[6]Y.Yang,W.S.Wang,J.G.Liu,et al.,Phys.Rev.B 89(2014)094518.
[7]Fa Wang and T.Senthil,Phys.Rev.Lett.106(2011)136402.
[8]J.W.Kim,et al.,Phys.Rev.Lett.109(2012)037204.
[9]Z.Y.Meng,Y.B.Kim,and H.Y.Kee,Phys.Rev.Lett.113(2014)177003.
[10]S.Sumita,T.Nomoto,and Y.Yanase,Phys.Rev.Lett.119(2017)027001.
[11]Y.K.Kim,et al.,Science 345(2014)187.
[12]A.de la Torre,et al.,Phys.Rev.Lett.115(2015)176402.
[13]Y.K.Kim,N.H.Sung,J.D.Denlinger,and B.J.Kim,Nat.Phys.12(2016)37.
[14]Y.J.Yan,et al.,Phys.Rev.X 5(2015)041018.
[15]Feng Ye,et al.,Phys.Rev.B 87(2013)140406(R).
[16]Chetan Dhital,et al.,Phys.Rev.B 87(2013)144405.
[17]G.Jackeli and G.Khaliullin,Phys.Rev.Lett.102(2009)017205.
[18]S.Fujiyama,et al.,Phys.Rev.Lett.108(2012)247212.
[19]N.B.Perkins,Y.Sizyuk,and P.W?lfle,Phys.Rev.B 89(2014)035143.
[20]J.M.Carter,V.Shankar,and H.Y.Kee,Phys.Rev.B 88(2013)035111.
[21]I.V.Solovyev,V.V.Mazurenko,and A.A.Katanin,Phys.Rev.B 92(2015)235109.
[22]D.Hsieh,F.Mahmood,D.H.Torchinsky,et al.,Phys.Rev.B 86(2012)035128.
[23]H.Watanabe,T.Shirakawa,and S.Yunoki,Phys.Rev.B 89(2014)165115.
[24]H.Watanabe,T.Shirakawa,and S.Yunoki,Phys.Rev.Lett.105(2010)216410.
[25]R.Arita,J.Kune? A.V.Kozhevnikov,et al.,Phys.Rev.Lett.108(2012)086403.
[26]H.Jin,H.Jeong,T.Ozaki,and J.J.Yu,Phys.Rev.B 80(2009)075112.
[27]P.T.Liu,et al.,Phys.Rev.B 92(2015)054428.
[28]S.J.Moon,et al.,Phys.Rev.B 80(2009)195110.
[29]Q.Li,et al.,Sci.Rep.3(2013)3073.
[30]A.Yamasaki,et al.,Phys.Rev.B 89(2014)121111(R).
[31]I.N.Bhatti and A.K.Pramanik,J.Magn.Magn.Mater.422(2017)141.
[32]D.Haskel,G.Fabbris,M.Zhernenkov,et al.,Phys.Rev.Lett.109 027204(2012).
[33]S.Fujiyama H.Ohsumi,K.Ohashi,et al.,Phys.Rev.Lett.112 016405(2014).
[34]G.L.Stamokostas and G.A.Fiete,Phys.Rev.B 97(2018)085150.
[35]S.Zhou,K.Jiang,H.Chen,and Z.Wang,Phys.Rev.X 7(2017)041018.
[36]C.Castellani,C.R.Natoli,and J.Ranninger,Phys.Rev.B 18(1978)4945.
[37]A.Georges,L.Medici,and J.Mravlje,Ann.Rev.Condens.Matter Phys.4(2013)137.
[38]M.E.A.Coury,S.L.Dudarev,W.M.C.Foulkes,et al.,Phys.Rev.B 93(2016)075101.
[39]S.Zhou and Z.Wang,Phys.Rev.Lett.105(2010)096401.
[40]Y.M.Quan,L.J.Zou,D.Y.Liu,and H.Q.Lin,Eur.Phys.J.B 85(2012)55.
[41]Q.Luo,K.Foyevtsova,G.D.Samolyuk,et al.,Phys.Rev.B 90 035128(2014).
[42]A.J.Kim,H.O.Jeschke,P.Werner,and R.Valentí,Phys.Rev.Lett.118(2017)086401.
[43]D.Pincini,et al.,Phys.Rev.B 96(2017)075162.
[44]X.Wu,F.Yang,C.Le,et al.,Phys.Rev.B 92(2015)104511.
 Communications in Theoretical Physics2018年7期
Communications in Theoretical Physics2018年7期
- Communications in Theoretical Physics的其它文章
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media?
- Galerkin Finite Element Study on the Effects of Variable Thermal Conductivity and Variable Mass Diffusion Conductance on Heat and Mass Transfer?
- The Three-Pion Decays of the a1(1260)?
- A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum?
- Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
