Numerical simulation of wave-current interaction using the SPH method *
Ming He (賀銘), Xi-feng Gao (高喜峰), Wan-hai Xu (徐萬海)
State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300350, China
The numerical wave-current tank (NWCT) is useful in studying the hydrodynamic performance of a newly-designed marine structure. Generally, it is built within the Eulerian framework. The superimposed flow velocity and the surface elevation are simultaneously specified at the inflow boundary to directly generate the wave-current field[1]. However, only a few wave-current cases can be realized limited to the wave-current interaction theory development. In other studies, the current is generated through a velocity inflow boundary and a pressure outflow boundary,and meanwhile a source function is incorporated into the mass or momentum conservation equations of the fluid to generate the wave[2]. The main drawback of this approach lies in its greater computational cost,since an extra sponge layer has to be set on the opposite side for the desired wave. Besides, the Eulerian NWCT also encounters difficulties in the studies concerning the fluid fragmentation and large displacement of the fluid- solid interface.
The recent popular smoothed particle hydrodynamics (SPH)[3]method conquers the drawbacks of conventional Eulerian method and shows promising prospects in simulations of complex fluid motion[4]and fluid-structure interaction[5]. Because the SPH method can imitate the physical activities factually,the wave can be generated by a wave paddle and absorbed by a sponge layer and the current can be driven with the usage of a pump system, just as they are produced in a laboratory tank. The key techniques of building an SPH NWCT lie in the circulation regulation of fluid particles between the inflow and outflow regions. Besides, it is also necessary to propose an approach towards shortening the time to reach the steady state of the wave-current field. In this work, the above two issues are briefly discussed.
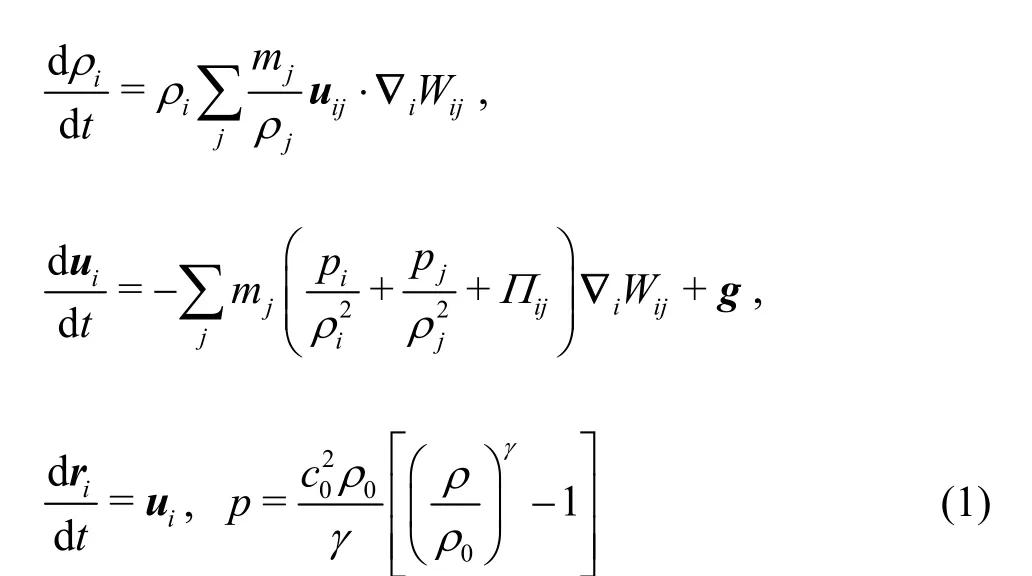
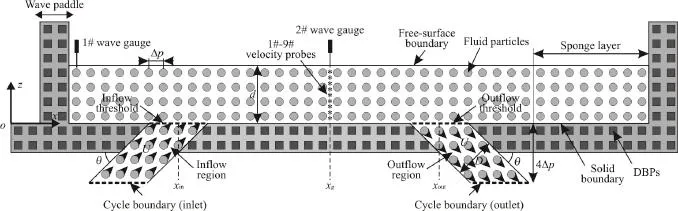
Fig. 1 Schematic diagram of the NWCT
The SPH governing equations of fluid is:where the labels i and j denote the target particle and its neighboring particle, respectively. ρ,p,m,g, r and u are the density, pressure, mass, gravitational acceleration, position and velocity, respectively.0ρ is the reference density.iju denotes u u.0c i s t h e s p e e d o f s o u n d. γ i s a c o n s t a n t
i j-which has the value of 7. Wij= W ( ri-rj,h) is the Wendland kernel function[6], where 1.5h p= Δ is the smoothing length and pΔ is the particle spacing.ij∏ is the artificial viscosity[7].
Since the pressure field of the SPH model is inherently noisy, a zero-order density filter[8]is used every 30 time steps to smooth the field quantities:

Figure 1 illustrates the SPH NWCT. For the fluid domain, apart from obeying the governing equations, three regions need to be additionally handled. One is the sponge layer arranged at the downstream of the tank. When fluid particles enter the sponge layer, their accelerations are artificially damped, resulting the outgoing waves dissipated[9].The other two are the inflow and outflow regions placed below the tank, where the directional velocity and hydrostatic pressure are simultaneously imposed.Mathematically, they are as follows:
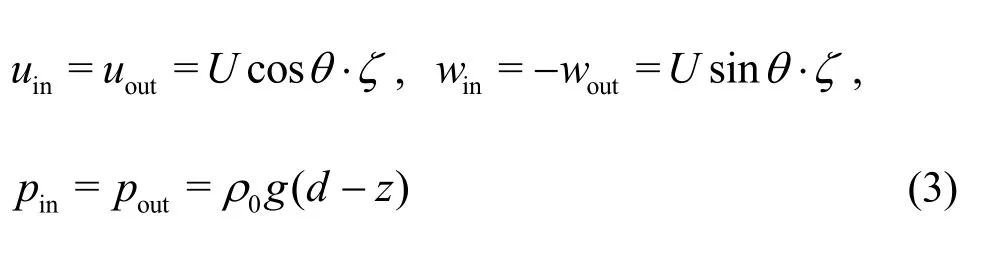
where u, w and U are the horizontal, vertical and axial flow velocities, respectively. θ is the inclination angle. ζ is a ramp function and reads:

where t0= U / D ( c0/ g )2is the buffering time, and D is the diameter of the inflow and outflow regions.
Cyclic boundary conditions are implemented at the bottoms of the inflow and outflow regions. The fluid particles which have escaped from the outlet are relocated back into the inflow region. The coordinate transformation is as follows:

where the labels esc and rlo denote the escaped and relocated fluid particles, respectively.inx and xoutdenote the center positions of inflow and outflow thresholds, respectively. With this cyclic boundary condition, the Lagrangian particles which should be lost owing to the directional flow in the outflow region are reused. Therefore, the global mass conservation is guaranteed.
The solid boundaries, including a piston-type wave paddle, a fixed right boundary and segmented fixed bottom boundaries are constructed using the dynamic boundary particles (DBPs). These DBPs share the same equations of continuity and state as the fluid particles, but their densities are further corrected[10]to reduce the unphysical pressure oscillations. Moreover, they do not follow the momentum equation. The DBPs fixed on the right and bottom boundaries remain stationary during the calculation, while those fixed on the wave paddle move based on the absorbing wave making theory[11].
To validate the SPH NWCT, the experiment of Umeyama[12]was reproduced. The physical parameters were: the water depthd=0.30 m , the wave heightH=0.0234 m , the wave periodT=1.0 s,the current velocityVx=0.08m/s , the diameter of inflow and outflow regionsD= 0.30 m , and the inclination angle =45θ°. The simulation was performed with =pΔ0.01m, requiring approximately 26 000 particles. The water surface elevation was measured by a wave gauge mounted atxg=3L,whereLis the wavelength. The flow velocity profile was measured by nine velocity probes uniformly distributed along the water depth direction.
Figure 2(a) gives the snapshot of the calculated wave profile in a wave-alone case and its comparison with the analytical solution. General agreement is observed, despite an approximately 15% on-way decrease in the predicted wave height. Figure 2(b)shows the multi-frame wave profiles with a time interval of 0.25T. As can be seen, the wave height and period are both steady during the wave propagation.When the wave enters the sponge layer, its amplitude decays in a linear pattern mainly due to the usage of the linear attenuation function in the sponge layer[10].At the end of the sponge layer, the surface fluctuation is almost eliminated. There is no significant rising of the mean water level, showing the good performance of the sponge layer.
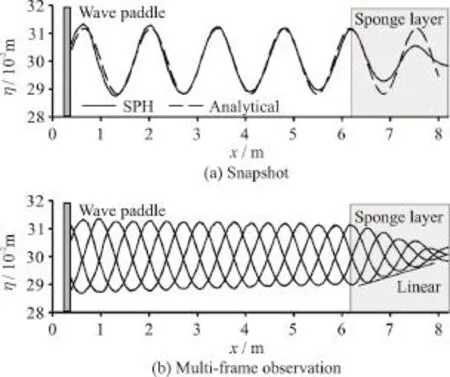
Fig. 2 Wave profiles for the wave-alone case
For the current-alone case, Fig. 3 compares the time evolutions of the horizontal flow velocities with the ordinary free-surface condition and under the temporary rigid-lid assumption. With the free-surface condition, the water surface rises above the inflow region and falls above the outflow region, thus resulting a low-frequency oscillatory flow at the beginning stage of the simulation. The quasi U-tube effect lasts for nearly 25 s before a steady state is reached, consuming enormous computational resources. However, with the temporary rigid-lid constraint, namely, the vertical positions and velocities of the fluid particles near the free surface are restricted within the first 2t0time, the potential energy contained in the fluctuated surface is transformed into the kinetic energy associated with the current flow. Therefore, the steady state can be reached as fast as 2 s in the present case. In addition,the horizontal flow velocities at different water depths,i.e.,z= 0.09 m, 0.15 m and 0.21 m, are basically consistent. It proves that a uniformly distributed current field along the water depth direction can be obtained.

Fig. 3 Horizontal flow velocities for the current-alone case
Figure 4 compares the calculated and measured water surface elevations in both wave-alone and wave-current cases. Satisfactory agreements are obtained. A further observation indicates the induced wave height in the wave-following-current case is smaller than that in the wave-alone case. Meanwhile,the induced wavelength is slightly longer than that in the wave-alone case. The former phenomenon can be theoretically explained by the conservation of the wave action flux, and the latter is due to the Doppler effect[2].
Figure 5 compares the calculated and measured horizontal-velocity profiles in the wave-current case.The overall trends of the calculated values agree well with the experimental data. However, the calculated velocity distributions are much smoother. The reason is twofold. First, the numerical calculation is 2-D,while the experiment is 3-D. Second, only 30 particles are arranged along the water depth direction herein,which may be insufficient to accurately describe the complex turbulent flow.

Fig. 4 Water surface elevations for both wave-alone and wavecurrent cases
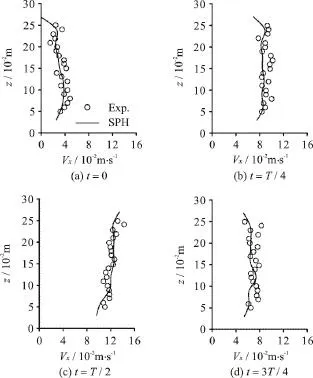
Fig. 5 Horizontal-velocity profiles for the wave-current case
It is well-known that in the wave-alone field the sign of the horizontal velocity changes alternately and the velocity amplitude near the water surface is larger than that below. However, in the wave-current field as observed from Fig. 5, the horizontal velocity is invariably positive although its amplitude varies periodically. Moreover, it is hard to judge in what water depth the flow velocity is larger.
In conclusion, the established SPH NWCT can accurately produce the wave-alone, current-alone and wave-current coexisting fields. The proposed temporary rigid-lid treatment turns out to be very effective for stabilizing the current field, and therefore signifycantly increase the computational efficiency. In the future, a validation in terms of the wave against the current will be conducted. The convergence of the SPH NWCT is also going to be checked.
[1] Xu Z. S., Chen Y. P., Tao J. F. et al. Modelling of a non-buoyant vertical jet in waves and currents [J].Journal of Hydrodynamics, 2016, 28(5): 778-793.
[2] Zhang J. S., Zhang Y., Jeng D. S. et al. Numerical simulation of wave–current interaction using a RANS solver [J].Ocean Engineering, 2014, 75: 157-164.
[3] Zhang A. M., Sun P. N., Ming F. R. et al. Smoothed particle hydrodynamics and its applications in fluidstructure interactions [J].Journal of Hydrodynamics, 2017,29(2): 187-216.
[4] Khayyer A., Gotoh H. On particle-based simulation of a dam break over a wet bed [J].Journal of Hydraulic Research, 2010, 48(2): 238-249.
[5] Ming F. R., Zhang A. M., Xue Y. Z. et al. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions [J].Ocean Engineering,2016, 117(1): 359-382.
[6] Wendland H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree[J].Advances in Computational Mathematics, 1995, 4(1):389-396.
[7] Monaghan J. J., Kajtar J. B. SPH particle boundary forces for arbitrary boundaries [J].ComputerPhysics Communications, 2009, 180 (10):1811-1820.
[8] Colagrossi A., Landrini M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics [J].Journal of Computational Physics, 2003, 191 (2):448-475.
[9] Ren B., He M., Dong P. et al. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method [J].Applied Ocean Research, 2015, 50:1-12.
[10] Ren B., He M., Li Y. et al. Application of smoothed particle hydrodynamics for modeling the wave-moored floating breakwater interaction [J].Applied Ocean Research, 2017, 67: 277-290.
[11] Hirakuchi H., Kajima R., Kawaguchi T. Application of a piston-type absorbing wavemaker to irregular wave experiments [J].Coastal Engineering in Japan, 1990,33(1): 11-24.
[12] Umeyama M. Coupled PIV and PTV measurements of particle velocities and trajectories for surface waves following a steady current [J].Journal of Waterway, Port,Coastal, and Ocean Engineering, 2011, 137(2): 85-94.
- 水動力學(xué)研究與進展 B輯的其它文章
- The influence of perforated plates on wave transmission and hydrodynamic performance of pontoon floating breakwater *
- URANS simulations of the tip-leakage cavitating flow with verification and validation procedures *
- Pressure characteristics of hydrodynamic cavitation reactor due to the combination of Venturi tubes with multi-orifice plates *
- Transport feasibility of proppant by supercritical carbon dioxide fracturing in reservoir fractures *
- Effect of blade shape on hydraulic performance and vortex structure of vortex pumps *
- Interaction between surface gravity wave and submerged horizontal flexible structures *

