Molecular Dynamics Simulations of the Elastic Anisotropy of Pd at Extreme Conditions?
Xiu-Lu Zhang(張修路),Yun-Xia Han(韓運(yùn)俠),Hong Jia(賈紅),Nuo Qu(曲諾),and
Zhong-Li Liu(劉中利)2,?
1Laboratory for Extreme Conditions Matter Properties,Southwest University of Science and Technology,
621010 Mianyang,China
2College of Physics and Electric Information,Luoyang Normal University,Luoyang 471022,China
1 Introduction
Shock response characteristics of materials may re flect how they behave under dynamic load with increasing pressure and temperature simultaneously,specifically along a fixed shock orientation.Palladium plays an important role in variety of applications such as dentistry,jewelery,catalysis,metalizing ceramics,hydrogen storage,and so on.[1]In addition,bulk Pd is frequently used as a pressure calibrator in high-pressure experiments because of its stable face-centered-cubic(fcc)structure under high pressure.Theoretical studies of shock response of Pd is of vital importance for it as a pressure calibrator,especially in the regions where experiments cannot reach.The elastic properties of materials at high pressures are necessary for us to understand their underlying static and dynamic responses to pressure,mechanical strength,and the equation of states.
The elastic anisotropy can be conveniently achieved from elastic constants for all crystal systems.Ab initiocalculations of elastic constants were often conducted at 0 K without any anharmonic effects,and the inclusion of temperature effects inab initioelastic constants are always complex and computationally expensive.However,the elastic constants of a crystal decrease by over 20%with increasing temperature.[2?5]The temperature dependence of the elastic constants of a material is crucial for predicting and understanding the mechanical strength and even phase transitions of a crystal.[6]Furthermore,elastic anisotropy resulted from the elastic constants has also many other implications in dislocation dynamics and even geophysical significance of materials.[7]It has been demonstrated that the elastic anisotropy in fluences the nanoscale precursor textures in shape memory alloys and other materials.[8?9]
It is known that molecular dynamics(MD)simulations naturally includes high-temperature anharmonic effects to any order beyond Debye temperature.[10?11]And they especially apply to high-temperature free energy calculations[12]and thermal fluctuation average,for instance in the calculation of elastic constants.The combination of MD with accurate interatomic potential of crystal systems provides a valid way to yield reliable elastic constants under high PT.
The rest of the paper is organized as follows.In Sec.2,we describe the details about the used interatomic potential of Pd and the computation method of high PT elastic constants.The results and discussion are addressed in Sec.3.Section 4 presents a short summary of the conclusions.
2 Methodology
We calculate the high pressure and temperature(PT)elastic constants of Pd using classical MD simulations.In order to accurately describe the interatomic interactions of Pd atoms,we adopt the embedded-atom-method(EAM)potential.[13?14]Our previous study[1]verified the high quality of the EAM potential of Pd in describing the high PT properties.For a system withNatoms,the total potential energyEtotis the sum of the embedding energyFand a pair potential?,
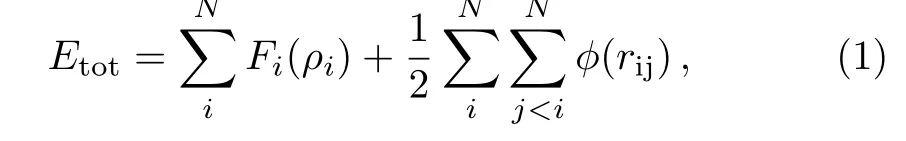
whererijis the distance from atomitoj.Fi(ρi)is the embedding energy,i.e.,the energy used to embed atomiinto the background electron densityρiof the rest atoms except atomj,

The high-temperature elastic constants of Pd are calculated based on direct deformation of the system by applying negative and positive strain of 5%of the lattice parameters in molecular dynamics simulation.Before applying deformations,the simulation box is fully relaxed in the NPT ensemble to equilibrate at the PT conditions,whereNis the number of particles,Pis the external pressure,andTis temperature.A Langevin thermostat is used in keeping the deformations of the system,with a damping parameter of 0.01 picoseconds(or 10 timesteps).This thermostat is used in combination with the microcanonical ensemble to perform Brownian dynamics.Deformations are tested to yield converged elastic constants.All the MD simulations are conducted with LAMMPS[15?16]package.The simulation box constructed from the multiplication 11×11×11 of face-centered-cubic(fcc)conventional unit cell containing 5324 atoms.
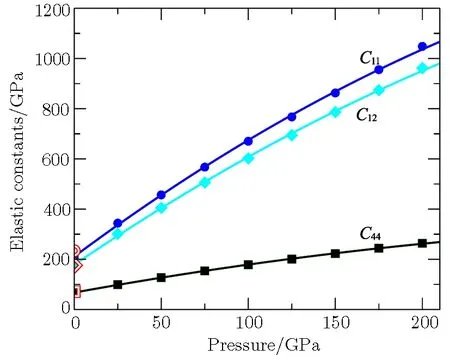
Fig.1 (Color online)The 300 K isothermal elastic constants of Pd as a function of pressure.The solid symbols are our calculated data.The lines are the second polynomial fit of the elastic constants.The red symbols are experimental values at 0 GPa.[17]
3 Results and Discussions
3.1 Isothermal Elastic Constants
The 300 K-isothermal elastic constants as a function of pressure are obtained and illustrated in Fig.1,in comparison with experimental data at 0 GPa.[17]All the three elastic constants,C11,C12andC44of the face-centeredcubic Pd,increase with pressure monotonically.While,it is found that they are actually not the linear functions of pressure.We find they are most fit to the second order polynomial function of pressure,
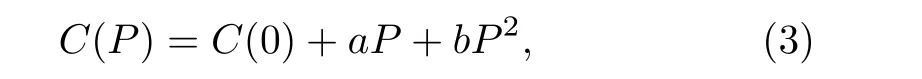
whereC(0)is the elastic constants at 0 GPa,andaandbare fitting parameters.
After fitting the second order polynomial function to the three sets of elastic constants data respectively,we yield the function

3.2 Isentropic Elastic Constants
The experimental elastic constants data[18?19]were isentropic data,therefore the calculated isothermal elastic constants should be converted in order to be compared with experiments.[5]For the cubic crystal,the conversion between isothermal and isentropic elastic constants are,[6]

whereBT=V(?2F/?V2)Tis the isothermal bulk modulus andβ=(?V/?T)P/Vis the volume thermal expansion coefficient.Such necessary data were achieved directly from our previous work.[12]


3.3 Sound Velocity Along Hugoniot
The obtained elastic constants and the corresponding Hugoniot PT points are listed in Table 1 and Fig.3(a),respectively.
The phase velocityvand polarization of the three waves along a fixed propagation direction defined by the unit vectorniare given by Cristoffel equation,
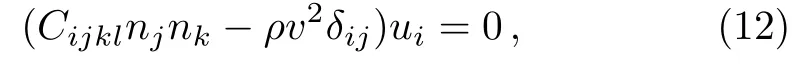
whereCijklis the fourth-rank tensor description of the elastic constants,nis the propagation direction,uthe polarization vector,andρthe density.From the Cristoffel equation,the isotropically averaged aggregate velocities are then derived as,

wherevP,vB,andvSare the compressional,bulk,and shear acoustic velocities,respectively.In Eqs.(13)and(15),the average isotropic shear modulusGof polycrystalline according to Voigt-Reuss-Hill approximations from single crystal elastic constants.The densityρin Eqs.(13),(14),and(15)are derived byρ=M/V,whereMis the molecular mass andVis the corresponding unit cell volume at specificPandT,illustrated in the inset of Fig.3(a).The equilibrium volumeV0of Pd at 0 GPa and 300 K is 14.86 A3.
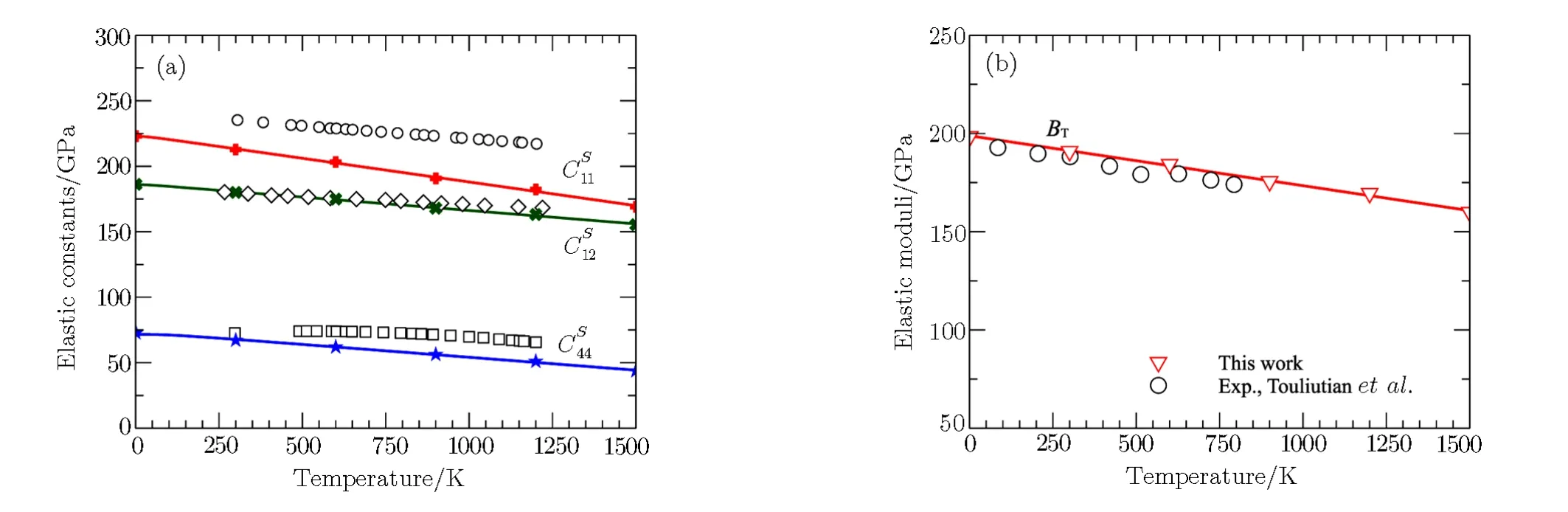
Fig.2 (a)High-temperature isentropic elastic constants of Pd at 0 GPa,in comparison with experimental data.Open symbols are experimental data from Refs.[21],respectively.(b)The calculated isothermal bulk moduli of Pd compared with experiment.[22]All the calculated moduli were fitted to the Varshni equation.[20]
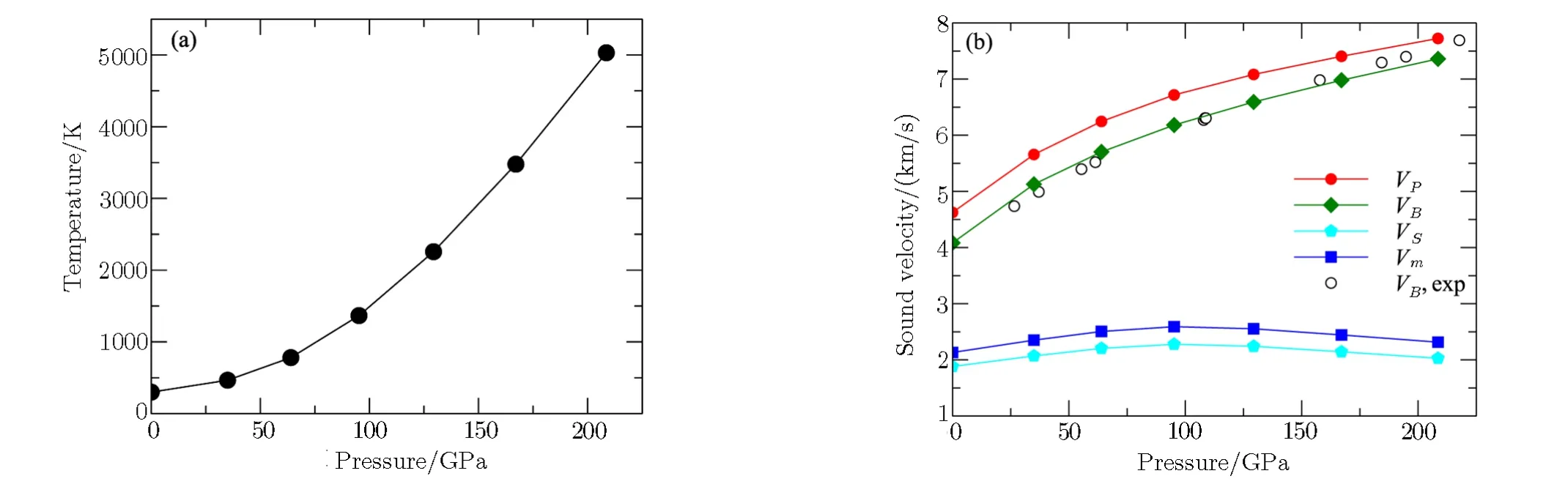
Fig.3 (a)The Hugoniot pressure-temperature relations.(b)The Hugoniot acoustic velocities of Pd compared with the experimental data.[23]
The average wave velocityvmis calculated from,

From elastic constant data we can calculate the Debye temperature ΘDfrom the average acoustic velocityvmvia the following equation:
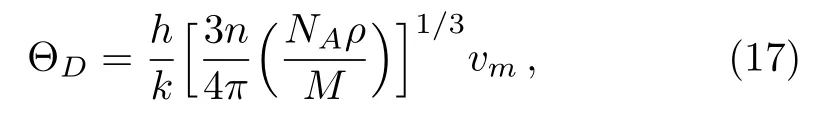
wherehis Planck’s constant,kthe Boltamann’s constant,NAthe Avogadro’s number,nthe number of atoms in the unit cell.
The acoustic velocities of Pd as a function of pressure along Hugoniot states are illustrated in Fig.3(b)in comparison with experimental data.The calculated compressional acoustic velocities are in very good agreement with experiment,[23]suggesting the elastic constants along Hugoniot states are accurate for further elastic anisotropy analyses.

Fig.4 Debye temperature of Pd at 0 GPa.
As shown in Fig.4,the Debye temperature of Pd along the Hugoniot states Debye temperature first has an abrupt jump and then has a slight decrease beyond~1000 K.The volume variation of Debye temperature are shown in the inset of Fig.4.Along Hugoniot states,Debye temperature is also not the linear functiong of volume.
3.4 Elastic Anisotropy Along Hugoniot
From Subsecs.3.1 to 3.3,we see that the calculated elastic constants re flect the high PT elastic behaviors of Pd very well. The mechanical anisotropy has an important implication in crystalline physics and engineering applications,[24]especially in understanding the dynamics response properties of Pd as a typical pressure calibrator.We here investigate the spacial anisotropy of Young’s modulus,shear modulus,and Poisson’s ratio to understand the mechanical anisotropy.Then the spacial orientation variation of the mechanical properties of Pd with PT are analyzed along the Hugoniot states.
The Young’s modulus,shear modulus,and Poisson’s ratio are all dependent on orientation.[24?25]It is specially interesting to uncover the evolution process of these elastic properties along the Hugoniot states.From the elastic constants,we calculate their orientation dependence for Pd along the Hugoniot states.Detailed method can be found in Ref.[25].In Fig.5 we plot the evolutional process of their 3D orientation dependence.In the[111]direction and the counterpart directions the maximum of Young’s modulus appears,but the anisotropy of Young’s modulus apparently increases with PT along Hugoniot states.The range of maximum in Young’s modulus becomes slim with increasing PT.Such increase of anisotropy can also be seen for the shear modulus in the second column of Fig.5,mainly implying in the orientational dependence of its minimum along Hugoniot states(green color).Negative Poisson’s ratio gradually appears and its absolute value increases with increasing PT,also suggesting the increase of the elastic anisotropy of Pd along Hugoniot states.
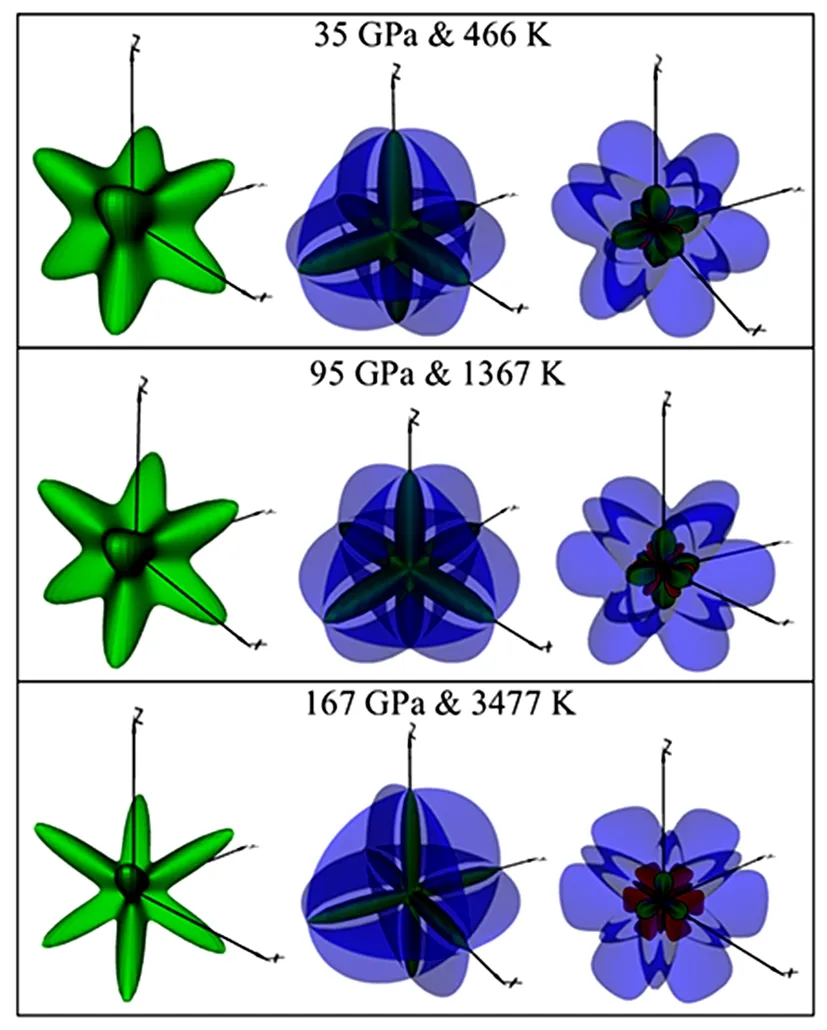
Fig.5 (Color online)The spacial orientation variation of the Young’s modulus,shear modulus,and poisson ratio of Pd along the principle Hugoniot.In the multi-colored figures,blue color accounts for maximum,green for minimum positive,red for negative.
In orderto understand thevariation ofelastic anisotropy of Pd along specific directions,the 2D Poisson’s ratio in the(110)plane is calculated and plotted in Fig.6.From Fig.6,we see that the maximum,minimum positive,and minimum negative values of Poisson’s ratios are distributed along[110]and[001]directions inhomogeneously.It is noteworthy that along some directions,such as[110],the positive and minimum negative values of Poisson’s ratios occur simultaneously.The simultaneous occurrence of positive and minimum negative Poisson’s ratios in the same direction indicates that the Poisson’s has the possibility of being negative.To understand the negative Poisson’s ratio,we need to recall the meaning of Poisson’s ratio.It is known that Poisson’s ratio is a measure of the extent to which the material contract in the directions perpendicular to the direction of stretching.The minimum negative value can be understood as the expansion in the[001]direction,which perpendicular to the[110]direction of stretching,while the maximum positive value corresponds to the normal contraction in[001]when stretching in[110]direction.

Fig.6 (Color online)2D representation of Poissons ratio in the(110)plane for Pd at(a)35 GPa and 466 K,(b)95 GPa and 1367 K and(c)167 GPa and 3477 K;maximum(blue),minimum positive(green)and minimum negative(red).
4 Conclusion
In conclusion,we have investigated the elastic properties of Pd under high PT systematically.Firstly,we calculate the isothermal elastic constants of Pd from molecular dyanmics simulations based on accurate interatomic potential.From the isothermal elastic constants,we deduce the high temperature isentropic elastic moduli of Pd and find they are in good agreement with experimental data at 0 GPa.Secondly,we achieve the acoustic velocities of Pd at high PT along Hugoniot states.The derived compressional wave velocity is also in good agreement with shock wave experiment.Finally,we investigate the elastic anisotropy of Pd along Hugoniot states.It is found that the spacial elastic anisotropy of Pd,re flected by the Young’s modulus,the shear modulus,the acoustic velocity and Poisson ratio,increases with increasing PT along Hugoniot states.
[1]Z.L.Liu,J.H.Yang,L.C.Cai,et al.,Phys.Rev.B 83(2011)144113.
[2]F.H.Featherston and J.R.Neighbours,Phys.Rev.130(1963)1324.
[3]D.Gerlich and E.S.Fisher,J.Phys.Chem.Solids 30(1969)1197.
[4]E.Walker and P.Bujard,Solid State Commun.34(1980)691.
[5]Y.Wang,J.J.Wang,H.Zhang,et al.,J.Phys.:Condens.Matter 22(2010)225404.
[6]O.Gulseren and R.E.Cohen,Phys.Rev.B 65(2002)064103.
[7]H.Ledbetter and A.Migliori,J.Appl.Phys.100(2006)063516.
[8]P.Lloveras,T.Castan,M.Porta,et al.,Phys.Rev.Lett.100(2008)165707.
[9]D.Legut,M.Friak,and M.Sob,Phys.Rev.Lett.99(2007)016402.
[10]I.Errea,M.Calandra,and F.Mauri,Phys.Rev.B 89(2014)064302.
[11]R.Car and M.Parrinello,Phys.Rev.Lett.55(1985)2471.
[12]Z.L.Liu,R.Li,X.L.Zhang,et al.,Comput.Phys.Commun.213(2017)122.
[13]M.S.Daw and M.I.Baskes,Phys.Rev.B 29(1984)6443.
[14]S.M.Foiles,M.I.Baskes,and M.S.Daw,Phys.Rev.B 33(1986)7983.
[15]S.J.Plimpton,J.Comp.Phys.117(1995)1.
[16]http://lammps.sandia.gov.
[17]J.A.Rayne,Phys.Rev.118(1960)1545.
[18]W.C.Overton and J.Ga ff ney,Phys.Rev.98(1955)969.
[19]Y.A.Chang and L.Himmel,J.Appl.Phys.37(1966)3567.
[20]Y.P.Varshni,Phys.Rev.B 2(1970)3952.
[21]M.Yoshihara,R.B.Mclellan,and F.R.Brotzen,Acta Metall.35(1987)775.
[22]Y.S.Touloukian,R.K.Kirby,R.E.Taylor,and T.Y.R.Lee,Thermophysical Properties of Matter,Plenum,New York(1970).
[23]T.S.Du ff y and T.J.Ahrens,J.Geophys.Res.97(1992)4503.
[24]Z.L.Liu,Y.P.Tao,X.L.Zhang,and L.C.Cai,Comput.Mater.Sci.114(2016)72.
[25]A.Marmier,Z.A.D.Lethbridge,R.I.Walton,et al.,Comput.Phys.Commun.181(2010)2102.
 Communications in Theoretical Physics2018年6期
Communications in Theoretical Physics2018年6期
- Communications in Theoretical Physics的其它文章
- Spontaneous Emission Originating from Atomic BEC Interacting with a Single-Mode Quantized Field
- Destroying a Near-Extremal Kerr-Newman-AdS Black Hole with Test Particles?
- Ordinary Mode Instability in a Cairns Distributed Electron Plasma
- Thermal Conductivity of Complex Plasmas Using Novel Evan-Gillan Approach
- Statistical Properties of a System Consisting of a Superconducting Qubit Coupled to an Optical Field Inside a Transmission Line
- In fluences of Crystal-Field and Interlayer Coupling Interactions on Dynamic Phase Diagrams of a Mixed-Spin(3/2,2)Bilayer System?
