Higgs and Bottom Quarks Associated Production at High Energy Colliders in the Littlest Higgs Model with T-Parity?
Biao-Feng Hou(侯鏢鋒), Hua-Ying Zhang(張華瑩),and Heng-Heng Bi(畢恒恒)
College of Physics and Materials Science,Henan Normal University,Xinxiang 453007,China
1 Introduction
The discovery of Higgs boson by the ATLAS[1]and CMS[2]collaborations is a great triumph both in theory and experiment.To ultimately establish its nature,it is necessary to perform a precise measurement,which is expected to achieve in the next phase of the LHC and future electron-positron collider.One of the important contents is the Yukawa coupling,which can play a key role in testing the Standard Model(SM)and probing the new physics.
Processes involving third generation quarks bring about special theoretical attention.On the one hand,bottom and top quarks have some very peculiar signatures with respect to light quarks that make an easy fl avor identi fication possible.On the other hand,being the heaviest among all quarks,they have the strongest Yukawa couplings so that they can be an appropriate probe for the electroweak symmetry breaking(EWSB)mechanism.Because of the small mass of bottom relative to top,studying the bottom Yukawa couplingbˉbHcan effectively probe new physics beyond the SM.Here,a Higgs production mode that features abˉbHcoupling is a viable alternative.There are two main such modes:the dominant one is a contribution to gluon fusion,where bottom-quark loop amplitudes interfere with top-quark loop amplitudes;the second-largest is Higgs and bottom quarks associated production.In this work,we will focus on the associated production processes at the LHC ande+e?collider.
As an extension of the SM,the littlest Higgs model with T-parity(LHT)[3]was proposed as a possible solution to the hierarchy problem and so far remains a popular candidate of new physics.In the LHT model,the Higgs boson is constructed as a pseudo-Nambu-Goldstone boson of the spontaneously broken global symmetry.Some new particles are predicted and some Higgs couplings are modi fied so that the Higgs properties in this model may be different from the SM.To probe these effects at experiments,various Higgs boson production processes are ideal places.
The paper is organized as follows.In Sec.2 we give a brief review of the LHT model.In Sec.3 and Sec.4 we investigate the Higgs production in association with bottom quarks at the LHC and thee+e?collider,respectively.Finally,we give a short summary in Sec.5.
2 A Brief Review of the LHT Model
The LHT model is based on an SU(5)/SO(5)nonlinearσmodel.At scalef~O(TeV),the global group SU(5)is spontaneously broken into SO(5)by the vacuum expectation value(VEV)of an SU(5)symmetric tensor Σ,which is given by

wheregandg′are the SM SU(2)Land U(1)Ygauge cou-plings,respectively.In order to match the SM prediction for the gauge boson masses,the VEVvis related to the SM Higgs VEVvSM(=246 GeV)through the following formula

In order to cancel the large radiative correction to the Higgs mass parameter induced by the top quark,the top quark Yukawa coupling must be modi fied.One must also introduce additional singlets,which transform under T-parity as

so the top quark Yukawa coupling is then given by


where?ijkand?xyare the antisymmetric tensors withi,j,k=1,2,3 andx,y=4,5,q1andq2are fermion SU(2)doublets,?is the image of Σ underT-parity,the superscript indenotes the third quark generation,λ1andλ2are two dimensionless top quark Yukawa couplings.
For the other quarks,it will not be necessary to modify the Yukawa Lagrangian as in the top sector since their Yukawa couplings are at least one order of magnitude smaller.Therefore,we do not need to introduce additional singlets for the remaining up-type quarks and the Yukawa coupling is accordingly given by


Here,there are two possiblechoices[4]forX:(denoted as case A)and(denoted as case B),whereis the(3,3)component of the fieldIn the two cases,the corrections to the Higgs couplings with the down-type quarks and charged leptons with respect to their SM values are given at orderby

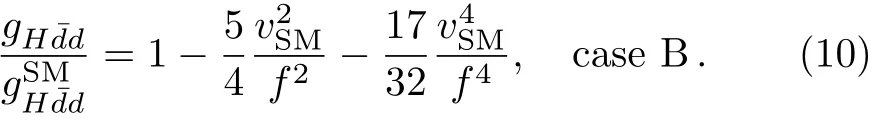
For clarity,we show the coupling ratiosRg(Hdˉd)=as a function of the scaleffor two cases in Fig.1(a).
In the LHT model,the new predicted particles and the modi fied Higgs couplings can in fl uence the branching ratios of the Higgs decay. Here,we show the ratiosas a function of the scaleffor two cases in the right panel of Fig.1(b).We can see that the branching ratios Br(H→γγ)are enhanced with respect to the SM values.

Fig.1The ratios Rg(Hdˉd)and RBr(H→γγ)as a function of the scale f.
3 Higgs and Bottom Quarks Associated Production at LHC
At the parton level,there are two ways to perform the computation,which are usually called four-and fivefl avour schemes(abbreviated with 4FS and 5FS henceforth,respectively). In the 4FS with nobquarks in the initial state,the lowest order exclusive processes areshown in Fig.2,where both bottom jets are tagged.In the 5FS,the lowest order inclusive process isshown in Fig.3,while if one demands that at least onebquark be observed,the leading semiinclusive process isbg→bHshown in Fig.4.

Fig.2 Feynman diagrams for in the 4FS.Not shown are diagrams that can be obtained by crossing the initial state gluons,or radiating the Higgs o ffan antibottom quark.

Fig.3 Feynman diagrams for
At the LHC,there are mainly three different types of production processes:i)the inclusive one,where no bottom quark jet is tagged,dominated by the bottom quark fusion processthe semi-inclusive one,where only one bottom quark is tagged,dominated by processbg→bH,iii)the exclusive one where both bottom jets are tagged,almost entirely dominated bywith only a small contribution from

Fig.4 Feynman diagrams for bg→bH.
We calculate the cross sections using the CalcHEP 3.6.25,[6]where the CTEQ6L[7]is used as the parton distribution function and the renormalization/factorization scale is set to beμR=μF=mH.In our calculations,the conjugate processes have been considered,unless otherwise noted. Considering the constraints in Ref.[8],we take the relatively loose parameter space 500 GeV≤f≤1500 GeV.The relevant SM parameters are taken as follows[9]


We show the relative correctionδσ/σas a function of the scaleffor case A and case B in Fig.5(a).We can see that the relative correctionsδσ/σare negative,which originates from the negativecoupling correction.The relative correctionsδσ/σare larger for case B due to the larger negative correction.Besides,the relative corrections of the three processes for case A are coinci-dent due to the samecoupling correction involved,and the similar things happened for case B.Due to the strong dependence of the leading order(LO)predictions for these processes on the renormalization/factorization scale,we also show the cross sections as a function of the renormalization/factorization scaleμforf=1000 GeV in Fig.5(b).We can see that the dependence of these three processes on the scaleμis different,where the processis most sensitive to the scaleμ.This dependence can be signi ficantly reduced when higher-order QCD corrections are included.

Fig.5 The relative correction δσ/σ as a function of the scale f and the cross sections as a function of the renormalization/factorization scaleμ.

Fig.6 The normalised distributions ofafter the basic cuts in the Higgs to diphoton channel at 14 TeV LHC for f=1000 GeV.
In order to investigate the observability,we display some kinematical distributions of the final states in theH→γγchannel.We generate the signal events by using MadGraph 5[10]and set the renormalization/factorization scaleμR=μF=mHto be the event-by-event value.The parton shower and hadronization are performed with PYTHIA,[11]and the fast detector simulations are performed with Delphes.[12]We show the normalised distribu-tions of the transverse momentumthe separation?Rγ1γ2and the invariant massMγ1γ2at 14 TeV LHC forf=1000 GeV in Fig.6 after the basic cuts

We can see that the peak of the ?Rγ1γ2is at?Rγ1γ2~3 for these three processes,which means that the two leptons incline to fl y back-to-back.Besides,we can see that the spreading of theγ1γ2invariant mass peaks atmHfor these three processes,which can be used to remove the backgrounds effectively through a narrow invariant mass cut.
4Production ate+e? Collider
At thee+e?collider,the dominant Higgs and bottom quarks associated production process isWe show the lowest order feynman diagrams of this process in Fig.7,which is almost entirely dominated by Fig.7(a)due to the smallcoupling.

Fig.7 Feynman diagrams for

Fig.8 The cross sections as a function of the scale f and the energy in the(un)polarized beams.
Considering the polarization of the initial electron and positron beams,the cross section ate+e?collider can be expressed as[13]

whereσRLis the cross section for completely right-handed polarizede?beam(pe=+1)and completely left-handed polarizede+beamand other cross sectionsσRR,σLLandσLRare de fined analogously. In the following calculations,we take the polarized beam withp(e?,e+)=(?0.8,0.3)and the same SM parameters as Sec.3.We calculate the cross sections using the CalcHEP 3.6.25 and set the renormalization/factorization scale
In Fig.8(a),we show the cross sections as a function of the scalefin(un)polarized beams for two typical energyWe can see that the cross sections can be enhanced obviously by the polarized beams.In order to see the dependence of the cross sections on the energy,we show the cross sections as a function of the energyin(un)polarized beams for two scalesf=(600,1000)GeV.
In order to investigate the observability,we display some kinematical distributions of final states through the channelwhich implies that the events contain one pair of photons and twob-jets.We generate the signal events by using MadGraph 5 and perform the parton shower and hadronization with PYTHIA.The fast detector simulations are performed with Delphes,where theis used.We show the normalised distributions of the transverse momentumand the invariant massin the Higgs to diphoton channel at 500 GeV-ILC forf=1000 GeV in Fig.9.Obviously,we can see that the spreading of theγ1γ2invariant mass peaks atmHand theb1b2invariant mass peaks atmZdue to the resonance effects.

Fig.9 The normalised distributions ofin the Higgs to diphoton channel at unpolarized 500 GeVILC for f=1000 GeV.
5 Summary
In this paper,we discuss the Higgs production in association with bottom quarks at the LHC and futuree+e?collider in the LHT model.For the LHC,we calculate the cross sections and the relative correction of processesFor thee+e?collider,we calculate the cross sections of processin(un)polarized beams.In order to investigate the observability,we display some typical final state distributions of these processes in the Higgs to diphoton channel,which will help to detect the signal at experiments.
[1]G.Aad,et al.,[ATLAS Collaboration],Phys.Lett.B 716(2012)1.
[2]S.Chatrchyan,et al.,[CMS Collaboration],Phys.Lett.B 716(2012)30.
[3]H.C.Cheng and I.Low,J.High Energy Phys.0309(2003)051;J.High Energy Phys.0408(2004)061;I.Low,J.High Energy Phys.0410(2004)067.
[4]C.R.Chen,K.Tobe,and C.P.Yuan,Phys.Lett.B 640(2006)263.
[5]D.A.Dicus and S.Willenbrock,Phys.Rev.D 39(1989)751;M.A.Aivazis,J.C.Collins,F.I.Olness,and W.K.Tung,Phys.Rev.D 50(1994)3102;J.C.Collins,Phys.Rev.D 58(1998)094002.
[6]A.Belyaev,N.D.Christensen,and A.Pukhov,Comput.Phys.Commun.184(2013)1729;A.Belyaev,C.R.Chen,K.Tobe,and C.P.Yuan,Phys.Rev.D 74(2006)115020.
[7]J.Pumplin,D.R.Stump,J.Huston,et al.,J.High Energy Phys.07(2002)012.
[8]X.F.Han,L.Wang,J.M.Yang,and J.Y.Zhu,Phys.Rev.D 87(2013)055004;B.F.Yang,G.F.Mi,and N.Liu,J.High Energy Phys.10(2014)047;N.Liu,L.Wu,B.F.Yang,and M.C.Zhang,Phys.Lett.B 753(2016)664;B.F.Yang,J.Z.Han,and N.Liu,Phys.Rev.D 95(2017)035010;H.Y.Wang and B.F.Yang,Adv.High Energy Phys.2017(2017)5463128.
[9]C.Patrignani,et al.,(Particle Data Group),Chin.Phys.C 40(2016)100001.
[10]J.Alwall,et al.,J.High Energy Phys.07(2014)079.
[11]T.Sjostrand,S.Mrenna,and P.Z.Skands,J.High Energy Phys.0605(2006)026.
[12]J.de Favereau,et al.,J.High Energy Phys.1402(2014)057.
[13]G.Moortgat-Pick,et al.,Phys.Rep.460(2008)131.
 Communications in Theoretical Physics2018年3期
Communications in Theoretical Physics2018年3期
- Communications in Theoretical Physics的其它文章
- A First-Principles Study on the Vibrational and Electronic Properties of Zr-C MXenes?
- Cole-Hopf Transformation Based Lattice Boltzmann Model for One-dimensional Burgers’Equation?
- Thermally Radiative Rotating Magneto-Nano fl uid Flow over an Exponential Sheet with Heat Generation and Viscous Dissipation:A Comparative Study
- Decoherence Effect and Beam Splitters for Production of Quasi-Ampli fied Entangled Quantum Optical Light
- Application of Connection in Molecular Dynamics
- Wilsonian Renormalization Group and the Lippmann-Schwinger Equation with a Multitude of Cuto ffParameters?
