盧肖勇 張小章 張志忠

1)(清華大學(xué)工程物理系,北京 100084)

2)(核工業(yè)理化工程研究院,天津 300180)

(2017年10月29日收到;2018年1月24日收到修改稿)

1 引 言

原子的選擇性光電離是原子蒸氣激光同位素分離中關(guān)鍵的一步,因為它直接影響分離過程的選擇性和目標(biāo)同位素的利用率.為了提高激發(fā)電離效率以及電離過程的同位素選擇性,科研人員對其中的原子選擇性光電離過程開展了大量的理論研究[1?7].這些研究中通常將原子蒸氣看作是光學(xué)薄介質(zhì),也就是認(rèn)為原子蒸氣介質(zhì)對激光脈沖沒有影響.然而在實際的激光同位素分離過程中,原子蒸氣的密度以及激光在作用區(qū)內(nèi)傳輸距離都是比較大的.實驗結(jié)果表明,脈沖激光通過光學(xué)厚原子蒸氣過程中不僅功率會發(fā)生顯著變化,同時還有脈沖延遲和脈沖變形[8?13],因此將原子蒸氣視作光學(xué)薄介質(zhì)來處理光電離過程是不合適的.為了從理論上更有針對性地開展研究,必須將原子蒸氣視為光學(xué)厚介質(zhì),在考慮它對脈沖激光影響的條件下研究光電離過程則更具實際意義.

有一些研究考慮了厚介質(zhì)條件下的電離過程,但是大多只考慮了原子蒸氣中的目標(biāo)同位素[14?17],主要關(guān)注了激光傳播路徑上激光脈沖的演化和空間單點(diǎn)電離率的變化[18?21],缺少對整個厚介質(zhì)中平均電離率和選擇性的研究,這是激光同位素分離理論研究的一個不足之處.本文考慮了光學(xué)厚介質(zhì)中兩種同位素的吸收過程對脈沖激光的影響,并計算了原子蒸氣中不同位置處激光脈沖形狀、兩種同位素的電離率和電離選擇性.在此基礎(chǔ)上,研究了原子蒸氣的平均電離率和平均選擇性隨激光參數(shù)和原子蒸氣參數(shù)的變化趨勢,并對上述參數(shù)給出了優(yōu)化方向.

2 數(shù)學(xué)理論模型

圖1為原子三步光電離模型,同位素A為目標(biāo)同位素,同位素B為非目標(biāo)同位素,原子受到3束激光的作用.前兩束激光可以將原子從基態(tài)激發(fā)到第2激發(fā)態(tài),第3束激光將原子激發(fā)到電離限之上的連續(xù)能區(qū),使原子電離.由于原子的第3步激發(fā)過程涉及連續(xù)態(tài)或者多電子激發(fā),所以在本文采用的密度矩陣方法中進(jìn)行了唯像處理.激光1,2與同位素A的能級躍遷共振,由于同位素位移的存在,這兩束激光對同位素B的激發(fā)是失諧的.設(shè)兩束激光沿著z方向傳播,其光場可以表示為

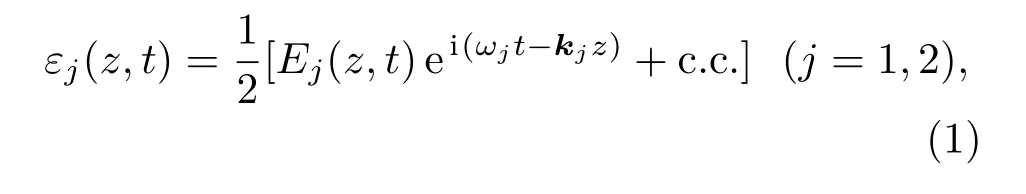
式中Ej(z,t)為激光場的復(fù)振幅;ωj為激光的圓頻率;kj為波矢.

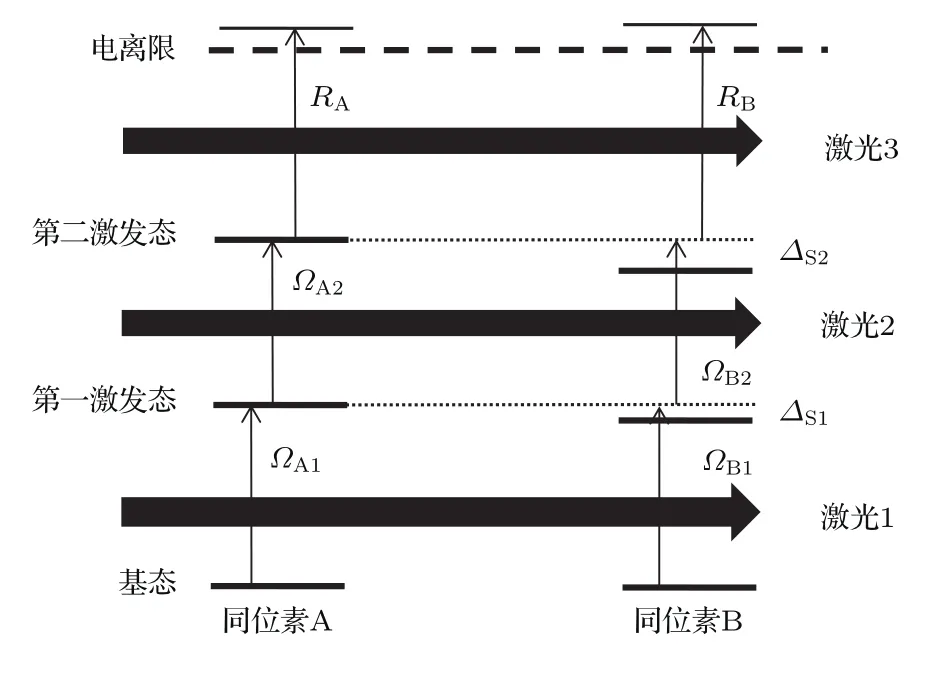
圖1 原子三步光電離路徑圖Fig.1.Schematic diagram of three-step photoionization of atom.

根據(jù)文獻(xiàn)[1],對電離躍遷做唯像處理之后,可以得到光傳播路徑上任意位置z處原子三步光電離的密度矩陣方程組為:

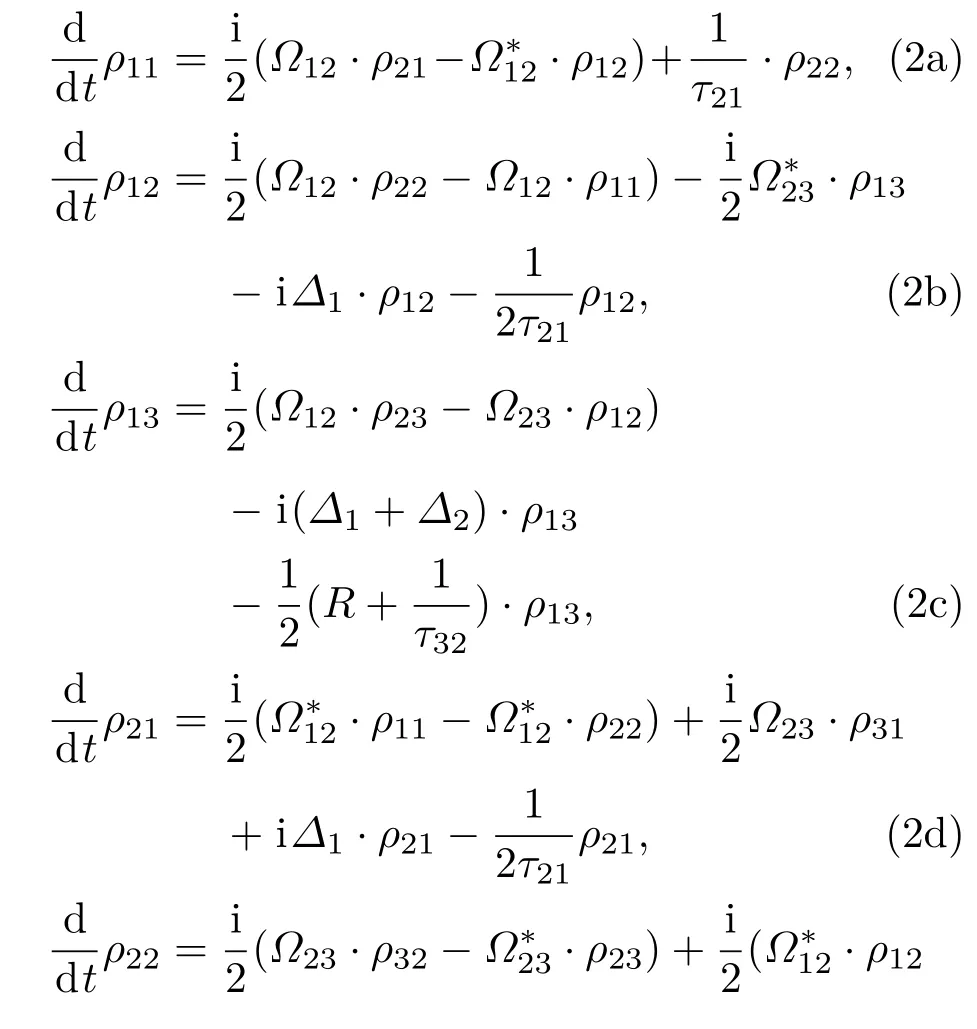
式中ρmn(m,n=1,2,3)為密度矩陣元;?1和?2為第1步和第2步躍遷的激光失諧量;τ21和τ32分別為第一激發(fā)態(tài)和第二激發(fā)態(tài)的自發(fā)輻射壽命;R為電離速率;?12和?23為第1步和第2步躍遷的Rabi頻率,其表達(dá)式為

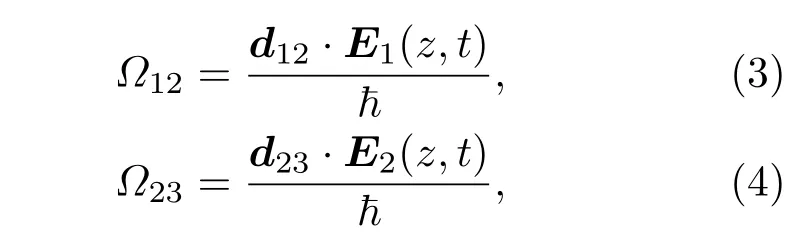
其中d12和d23為原子躍遷的電偶極矩.(2a)—(2i)式表示成矩陣形式則為

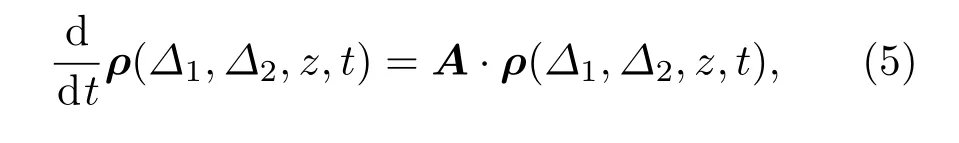
式中ρ(?1,?2,z,t)=[ρ11ρ12···ρ33]T,對于原子蒸氣中存在A,B兩種同位素的情況,A和B躍遷的動力學(xué)方程分別為:

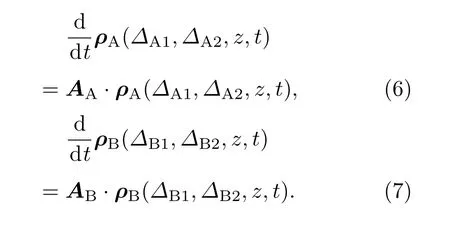
激光場在原子蒸氣介質(zhì)中的傳播采用慢變振幅近似下的Maxwell方程描述[9]:

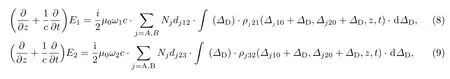
式中μ0為真空磁導(dǎo)率;ω1,ω2分別為兩束激光的圓頻率;c為真空光速;Nj(j=A,B)為兩種同位素的原子數(shù)密度;?j10和?j20為激光失諧量,是原子吸收譜線中心波長與激光波長的差;f(?D)為原子吸收譜線的線型函數(shù),?D為原子吸收譜線的Doppler展寬.取延時坐標(biāo),做如下變換:t′=t?z/c,ξ=z,則(6)—(9)式變?yōu)?/p>

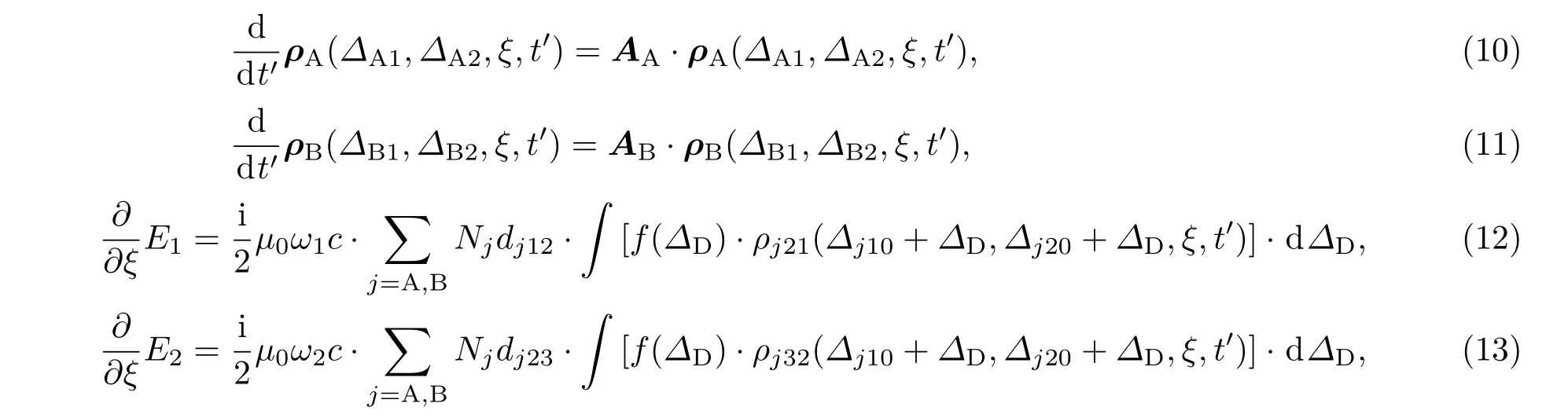
(10)—(13)式即為激光在原子蒸氣介質(zhì)中傳播的耦合方程組.一般情況下,(10)—(13)式方程組無法求得解析解,因此本文采用數(shù)值方法求解.對密度矩陣方程(10)式和(11)式用4階Runge-Kutta方法求解,對Maxwell方程(12)式和(13)式采用預(yù)報校正方法求解[22,23].

設(shè)t0時刻兩束激光脈沖均完全穿越原子蒸氣,則原子蒸氣中不同位置ξ處同位素A,B的電離率由(14)式得到

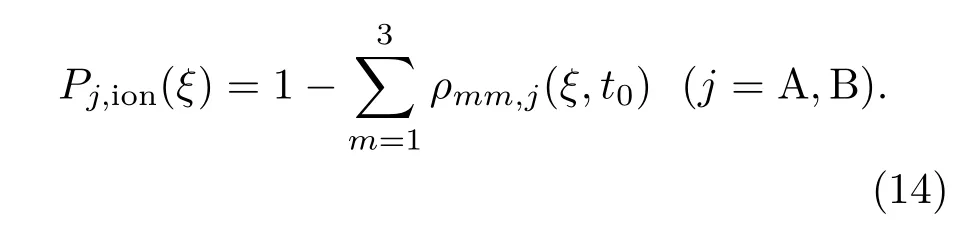
對于厚度為L的原子蒸氣介質(zhì),其平均電離率Pj,ion和平均選擇性S計算式分別為

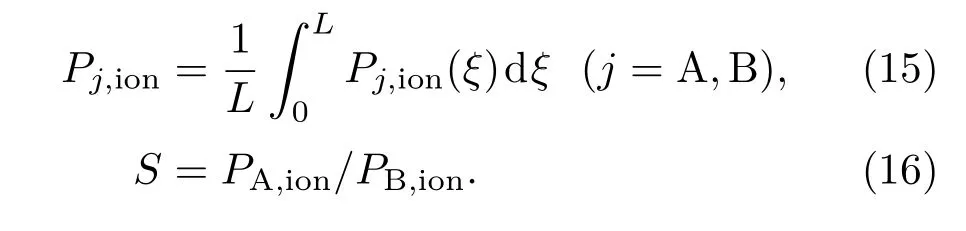
3 結(jié)果與討論

在以下的計算結(jié)果中,如不做額外說明,均使用以下計算參數(shù):同位素A原子密度NA=1.0×1018m?3;兩步躍遷的偶極矩dA12=1.0×10?30C·m,dA23=1.0×10?30C·m;第一激發(fā)態(tài)和第二激發(fā)態(tài)壽命分別為40 ns和100 ns;電離速率RA=0.2×109s?1,同位素B和同位素A的以上參數(shù)相同.原子吸收譜線的Doppler展寬為600 MHz.兩步激光波長均取為500 nm,脈寬30 ns,激光脈沖的形狀為Gauss型,其峰值對應(yīng)的電場強(qiáng)度均為2.0×105V/m,兩束激光之間無延時.兩束激光與同位素A共振,與同位素B兩個躍遷的失諧量分別為?S1=2.0 GHz,?S2=2.0 GHz.

圖2為不同傳播距離處的激光脈沖形狀.圖3表示在圖2的計算條件下,不同傳播距離處兩種同位素的電離率及該處的選擇性.從圖2可以看出,兩束脈沖在介質(zhì)中的損耗情況存在差異:第一,原子的第1步躍遷先于第2步躍遷,因此隨著傳播距離的增加,第1束激光的損耗集中在脈沖的前端(圖2中激光脈沖左側(cè)),第2束激光的損耗主要集中在后端;第二,光電離過程中原子在基態(tài)和第一激發(fā)態(tài)布居數(shù)的不同,原子蒸氣介質(zhì)對兩束激光的折射率存在差異,這導(dǎo)致第1束激光在介質(zhì)中的傳播速度小于第2束激光.上述兩個過程共同作用使兩束激光在傳播過程中產(chǎn)生相對延時,激光的激發(fā)強(qiáng)度減弱,最后導(dǎo)致了兩種同位素的電離率下降.由于非目標(biāo)同位素是失諧激發(fā)的,這種電離率下降對非目標(biāo)同位素更為明顯,所以選擇性反而會升高.當(dāng)兩束激光在時間上完全分開后,如圖2中7 m之后的位置,第一激發(fā)態(tài)自發(fā)輻射會造成第1束激光的損耗,第1束激光脈沖在介質(zhì)中傳播時逐漸損耗并消失,第2束激光脈沖則相當(dāng)于在真空中傳播,脈沖形狀不發(fā)生變化,電離率降為0.

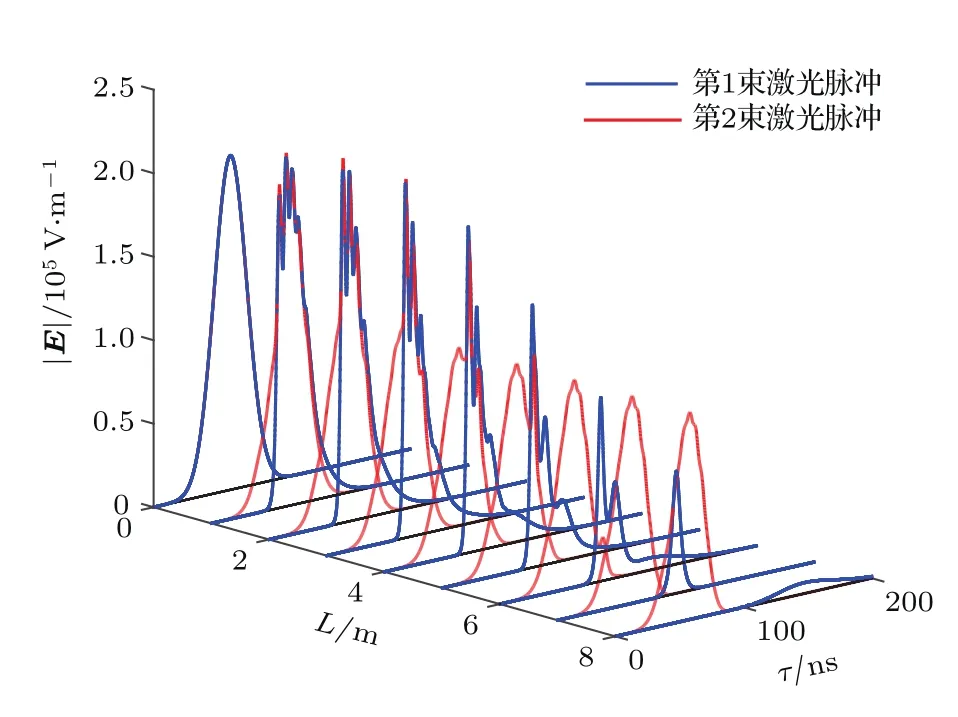
圖2 激光脈沖形狀在原子蒸氣介質(zhì)中的演化Fig.2.Evolution of laser pulse shape in a thick atom vapor medium.

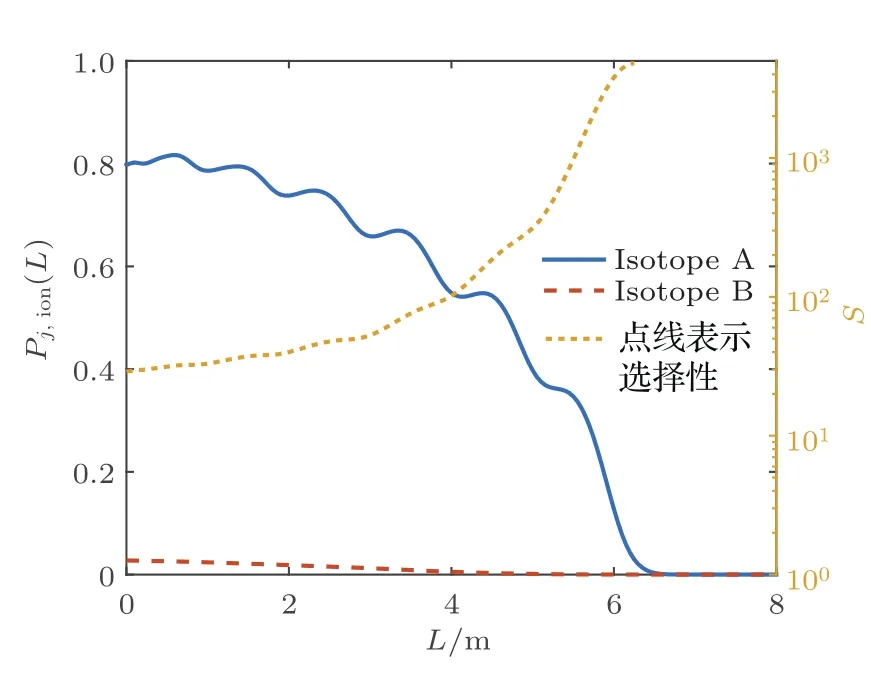
圖3 電離率和選擇性隨空間位置的變化Fig.3.Variation of ionization yield and selectivity with space distribution.

圖4 為第1束激光強(qiáng)度取不同值時,原子的平均電離率(此處的平均電離率均指同位素A的平均電離率,下同)和平均選擇性隨原子蒸氣厚度的變化曲線.設(shè)定平均選擇性停止增加的位置為激光的有效電離長度(見圖4箭頭).可以看出,隨著激光強(qiáng)度的增加,兩束激光在更長的傳播距離內(nèi)保持同步,其有效電離長度增加.對于較厚的原子蒸氣,平均電離率隨著激光強(qiáng)度的增加而增加;而對于相對較薄的原子蒸氣,比較圖4(a)中的3條曲線可以發(fā)現(xiàn),第1束激光強(qiáng)度的增加則使平均電離率下降,這是因為激光過強(qiáng)會引起原子在基態(tài)和第一激發(fā)態(tài)之間快速的布居振蕩,影響了后續(xù)的激發(fā)電離過程,當(dāng)?shù)?束激光的光強(qiáng)很大時也有此現(xiàn)象[3,19,24].而隨著激光線寬和原子吸收譜線Doppler展寬的增加,這種現(xiàn)象會逐漸減弱至消失.因此,當(dāng)原子蒸氣的厚度相對較小時,選擇低的激光強(qiáng)度有利于同時獲得高的平均選擇性和平均電離率,而對于激光同位素分離中的厚原子蒸氣介質(zhì),激光功率的增大可以提高原子的電離率,但是會使光電離的選擇性下降.

圖5為原子蒸氣厚度一定時(L=8 m),兩種同位素的平均電離率和平均選擇性隨兩束激光脈寬的變化曲線(單個激光脈沖的能量保持不變).可以看出,隨著激光脈寬的增大,同位素A的平均電離率有小幅度提高,而同位素B平均電離率的下降則十分明顯,這是因為隨著激光脈寬的增加,脈沖作用時間內(nèi)的激光功率下降,由于同位素A原子為過飽和激發(fā),功率下降對其激發(fā)電離速率影響不大,脈沖寬度的增加則可以提高激發(fā)電離過程的時間,因此電離率升高,對于光學(xué)薄介質(zhì)亦有此現(xiàn)象[25,26];而同位素B由于為非共振激發(fā),對脈沖作用時間內(nèi)的功率下降更為敏感,因此其電離率下降,相應(yīng)的平均選擇性有較大幅度的提高.因此在光電離過程中應(yīng)盡量增加激光脈沖寬度.

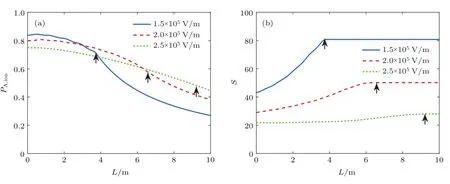
圖4 (a)平均電離率和(b)平均選擇性隨原子蒸氣厚度的變化Fig.4.Variation of(a)average ionization yield and(b)average selectivity with thickness of atom vapor.

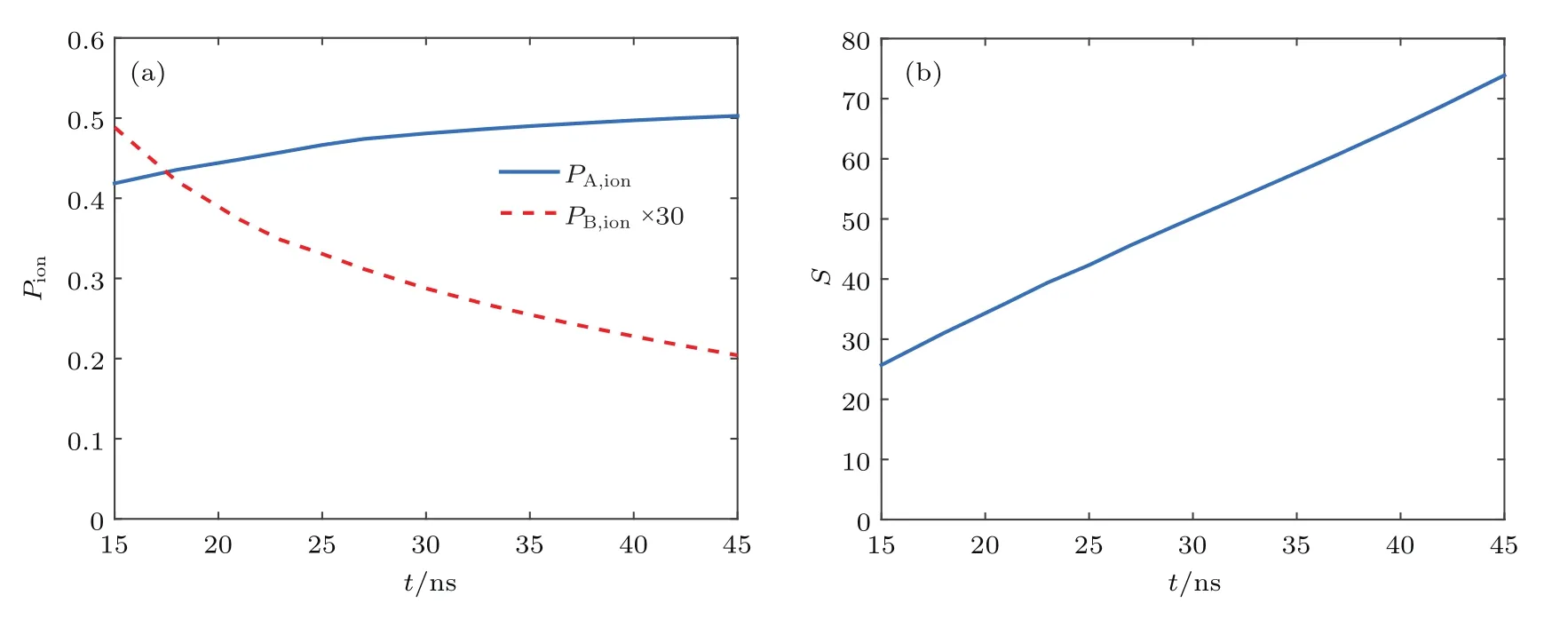
圖5 (a)平均電離率和(b)平均選擇性隨激光脈寬的變化Fig.5.Variation of(a)average ionization yield and(b)average selectivity with laser pulse width.

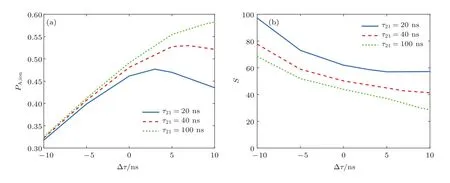
圖6 (a)平均電離率和(b)平均選擇性隨激光延時的變化Fig.6.Variation of(a)average ionization yield and(b)average selectivity with laser pulse time delay.

圖6 為原子蒸氣厚度一定(L=8 m),當(dāng)?shù)谝患ぐl(fā)態(tài)壽命取不同值時,同位素A的平均電離率和平均選擇性隨激光延時的變化曲線,假設(shè)第1束激光相對第2束激光超前時延時為正.從圖6中可以看出,存在一個最佳正激光延時,使同位素A原子的平均電離率達(dá)到最大.這是因為隨著激光延時的增大,第2束激光脈沖前端的能量也得到利用,且由于第1束激光脈沖的傳播速度小于第2束激光脈沖,有效電離長度增加,因此同位素A的平均電離率增加;當(dāng)激光延時繼續(xù)增大,則第1束激光脈沖的前端僅使原子在基態(tài)和第一激發(fā)態(tài)間做Rabi振蕩,直到第2束激光到來時才會有后續(xù)的激發(fā)電離過程,這相當(dāng)于第1束激光的有效強(qiáng)度減弱了,因此平均電離率下降.與已發(fā)表的薄介質(zhì)中激光延時對電離過程影響的文獻(xiàn)[27,28]相比較發(fā)現(xiàn),為了獲得更高的電離率,薄介質(zhì)光電離過程中激光延時的設(shè)置可以使更多的原子處于高激發(fā)態(tài);而厚介質(zhì)中激光延時的設(shè)置則更多地考慮到傳播路徑上兩束光的同步傳播.且最佳正激光延時隨著原子第一激發(fā)態(tài)壽命的增加而增加.圖6(b)則顯示平均選擇性隨著激光延時的變化趨勢與平均電離率相反.因此在光電離過程中,應(yīng)當(dāng)綜合考慮目標(biāo)同位素的電離率和選擇性兩方面來選擇合適的激光延時.

圖7為原子蒸氣厚度一定(L=8 m),當(dāng)兩束激光的脈沖寬度取不同值時,同位素A的平均電離率和平均選擇性隨激光延時的變化曲線.從圖7中可以看出,隨著激光脈寬的增加,同位素A的平均電離率和平均選擇性得到了同時提高,且當(dāng)激光延時為負(fù)值時,平均電離率的提高尤為明顯.另外,從圖7(a)中也可以看出,激光脈寬的增加也使平均電離率隨延時變化的曲線變緩、最佳激光延時增大.這說明在實驗時增加激光的脈沖寬度,不僅有利于同時提高平均電離率和平均選擇性,還可以降低對激光脈沖之間相對延時的控制精度.

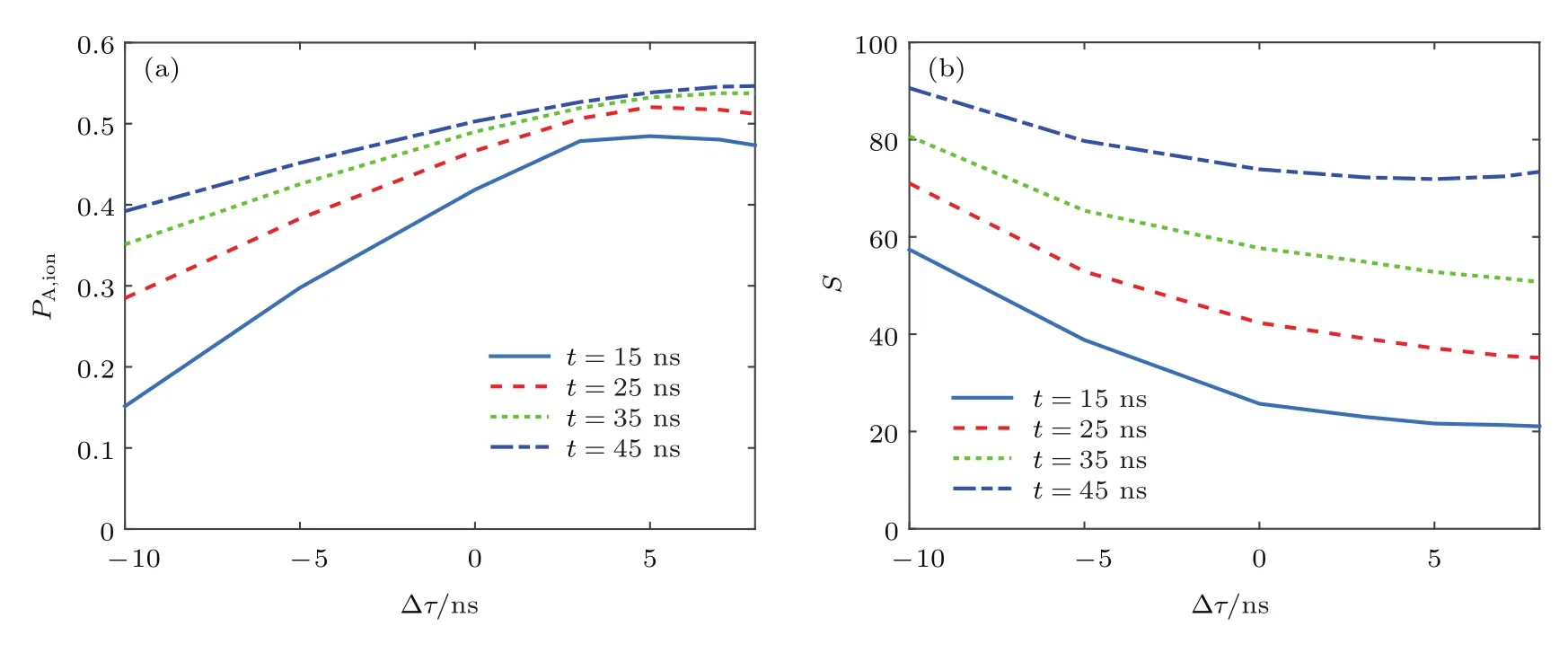
圖7 不同激光脈寬下(a)平均電離率和(b)平均選擇性隨激光延時的變化Fig.7.Variation of(a)average ionization yield and(b)average selectivity with laser pulse time delay for dif f erent laser pulse widths.

4 結(jié) 論

在考慮厚原子蒸氣介質(zhì)中同時存在的兩種同位素都與激光有相互作用的情況下,對厚介質(zhì)中目標(biāo)同位素的平均電離率和平均選擇性進(jìn)行了計算,得到了如下的結(jié)論:兩束同時發(fā)射的激光脈沖在介質(zhì)中傳播時會產(chǎn)生相對延遲,導(dǎo)致在激光傳播路徑上,原子蒸氣單點(diǎn)的電離率下降,選擇性升高.對于較厚的原子蒸氣介質(zhì),增加激光功率可以使平均電離率升高,但是平均選擇性則會下降;對于較薄的介質(zhì),適當(dāng)?shù)亟档图す夤β蕜t可以同時提高平均電離率和平均選擇性.在原子蒸氣參數(shù)不變的條件下,存在一個正的激光延時使平均電離率達(dá)到最大,平均選擇性隨激光延時的變化趨勢則與電離率相反.另外,固定單個激光脈沖的能量,盡量延長激光脈沖的寬度不僅可以同時提高目標(biāo)同位素的平均電離率和平均選擇性,還可以降低對激光脈沖之間相對延時的控制精度.

[1]Wang D W 1999Theory and Application of Laser Isotope Separation(Beijing: Atomic Energy Press)pp167–170(in Chinese)[王德武 1999激光分離同位素理論及其應(yīng)用(北京:原子能出版社)第167—170頁]

[2]Yuan K X,Yu C J 1994J.Atom.Mol.Phys.11 71(in Chinese)[袁奎訓(xùn),于長江 1994原子與分子物理學(xué)報 11 71]

[3]Fan F Y,Wang L J 2011Acta Phys.Sin.60 093203(in Chinese)[范鳳英,王立軍 2011物理學(xué)報 60 093203]

[4]Qi X Q,Wang F,Dai C J 2015Acta Phys.Sin.64 133201(in Chinese)[戚曉秋,汪峰,戴長建2015物理學(xué)報64 133201]

[5]Saleem M,Hussain S,Rafiq M,Baig M A 2006J.Appl.Phys.100 053111

[6]Wang L J,Yu H Y 2004Acta Phys.Sin.53 4151(in Chinese)[王立軍,余慧鶯 2004物理學(xué)報 53 4151]

[7]Das R M,Chatterjee S,Iwasaki M,Nakajima T 2015J.Opt.Soc.Am.B32 1237

[8]Siddons P 2014J.Phys.B:At.Mol.Opt.47 093001

[9]Li fl2006Advanced Laser Physics(Beijing:Higher Education Press)pp128–138(in Chinese)[李福利 2006高等激光物理學(xué)(北京:高等教育出版社)第128—138頁]

[10]Nomaru K,Izawa Y,Nakai S,Chen Y W,Yamanaka C 1994J.Nucl.Sci.Technol.31 914

[11]Nomaru K,Izawa Y,Nakai S,Chen Y W 1997J.Nucl.Sci.Technol.34 1147

[12]Yi J,Park H,Rhee Y,Lee J 2000Jpn.J.Appl.Phys.39 1128

[13]Ji W,Wu C,Raymer M G 2007J.Opt.Soc.Am.B24 629

[14]Jiang M H,Lin F C 1990Acta Phys.Sin.39 1887(in Chinese)[蔣孟衡,林福成 1990物理學(xué)報 39 1887]

[15]Xiao L,Lin F C 1998Acta Opt.Sin.18 1001(in Chinese)[肖玲,林福成 1998光學(xué)學(xué)報 18 1001]

[16]Chen Y W,Izawa Y,Nakai S,Yamanaka C 1995Jpn.J.Appl.Phys.34 504

[17]Xuan K D,Minh D H,Van D L,Huy B N 2017Optik131 497

[18]Jiang M H,Lin F C 1991Acta Opt.Sin.11 769(in Chinese)[蔣孟衡,林福成 1991光學(xué)學(xué)報 11 769]

[19]Xie S L,Wang D W,Ying C T,Zhu X H 1998Chin.J.Laser25 65(in Chinese)[謝世亮,王德武,應(yīng)純同,諸旭輝1998中國激光25 65]

[20]Xiao L,Lin F C 1999Acta Opt.Sin.19 1009(in Chinese)[肖玲,林福成 1999光學(xué)學(xué)報 19 1009]

[21]Chen Y W,Yamanaka C,Niki H,Adachi S,Izawa Y,Nakai S 1994J.Opt.Soc.Am.B11 1585

[22]Zhang H R,Li C,Yu X Y 2010Acta Phot.Sin.39 6(in Chinese)[張華榮,李成,余向陽 2010光子學(xué)報 39 6]

[23]Li C,Zhang H R,Yu X Y 2009Acta Sci.Nat.Univ.Sunyatseni.48 36(in Chinese)[李成,張華榮,余向陽2009中山大學(xué)學(xué)報(自然科學(xué)版)48 36]

[24]Xie S L,Wang D W,Ying C T 1997Chin.J.Nucl.Sci.Eng.17 166(in Chinese)[謝世亮,王德武,應(yīng)純同 1997核科學(xué)與工程17 166]

[25]Lu B S,Cui Z F 1998J.Atom.Mol.Phys.15 553(in Chinese)[盧秉嵩,崔執(zhí)鳳 1998原子與分子物理學(xué)報 15 553]

[26]Wang X L,Yao G X,Zhang X Y,Xu X S,Feng E Y,Ji X H,Cui Z F 2005Chin.J.Laser32 1211(in Chinese)[汪小麗,姚關(guān)心,張先熠,許新勝,鳳爾銀,季學(xué)韓,崔執(zhí)鳳2005中國激光32 1211]

[27]Liu B,Ning X J 2001Phys.Rev.A64 013401

[28]Li Z M,Zhu F R,Deng H,Ren X J,Zhai L H,Wang C H,Zhang L X 2006J.Atom.Mol.Phys.23 185(in Chinese)[李志明,朱鳳蓉,鄧虎,任向軍,翟利華,王長海,張利興2006原子與分子物理學(xué)報23 185]