Which Information Theoretic Quantity Should We Choose for Steric Analysis of Water Nanoclusters (H2O)n (n = 6, 32, 64)?
ALIPOUR Mojtaba
Department of Chemistry, College of Sciences, Shiraz University, Shiraz, Iran.
1 Introduction
As one of the key concepts in chemistry, steric effects have long been known to play imperative roles in various fields of science such as chemistry, biochemistry, pharmacology, etc.1. Steric effect is related to this fact that atoms and molecules occupy a certain space volumes. The hindrance induced when they are brought together changes various factors like energy, shape, reactivity. Notwithstanding qualitative considerations on the steric effects, like many other concepts in science there is no exact quantitative description of this effect. As a matter of fact, there is no physically observable variable associated with the steric effect and quantum mechanically speaking it is a noumenon2-5. Aiming to propose a quantitative scheme in this respect, a density functional theory (DFT)6-9description of the steric effects has pragmatically been proposed by Liu10. This approach is based on a new energy partition scheme in which the total electronic energy is decomposed into contributions from three independent parts steric, electrostatic, and fermionic quantum effects, leading to the steric energy ES[ρ] in terms of electron density ρ(r) and its gradient as follows
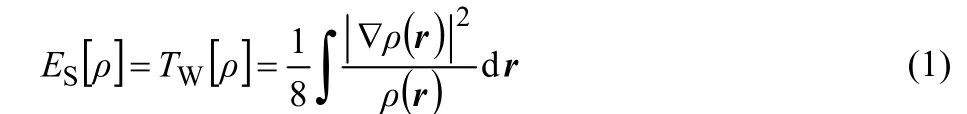
where TW[ρ] is the Weizs?cker kinetic energy11. Following the original paper,10this proposal has been employed for different purposes, see for instance Refs.12-25. We have also proposed another version of quantitative description of steric effects in momentum space and tested the resulting expressions for some phenomena in which the steric effects come into play17,19.
From a different perspective, the definition of steric energy in Eq.(1) is related to the Fisher information functional IF[ρ]26of information theory26-29,

In more details, Eq.(1) without the multiplying factor 1/8 is the definition of Fisher information and therefore the steric energy can be rewritten as ES[ρ] = (1/8)IF[ρ]. Information theory is a branch of applied mathematics, electrical engineering, and computer science which deals with the quantification of information which is often a probability distribution function. In recent years, much effort has been devoted for understanding and description of the physical and chemical processes in the framework of the information theory30-44.
Considering this point that the ground state electron density determines everything, various information theoretic functionals should be related45-47.Accordingly, we anticipate that the quantitative description of the steric effect can be rationalized based on information theoretic quantities other than Fisher information, as has been shown in our recent study48. On the other hand, it has also been revealed that the quantitative definition of steric effect in Eq.(1) and consequently Fisher information provide a quantitative tool for description of the trend of relative order of stability in molecular nanoclusters49,50. Putting all these perceptions together, it can be expected other information theory functionals should also be able to reproduce the relative energies of nanoclusters. Perusing this issue and comparing the obtained results from different information theoretic quantities for the steric effects of water nanoclusters constitute the subjects of the present investigation. In short, we plan to identify which information theoretic quantity is able to better describe the relative energies of water nanoclusters and whether or not it reveals any superiority over other functionals.
2 Information theoretic quantities
In addition to Fisher information, the central information theory functionals of concern are Shannon entropy Ss[ρ]27, Onicescu information energy EO[ρ]28, and Ghosh-Berkowitz-Parr (GBP) entropy SGBP[ρ]29. These functionals are respectively defined as follows
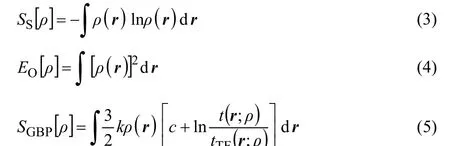
Regarding the functionals of information theory, several points are in order. From the information theory viewpoint, Shannon entropy is a global measure of the spatial delocalization of the electron density while Fisher information is a local measure of the sharpness or localization of the electron density. Considering the discrete forms of the Shannon entropy and Fisher information instead of continuous forms, using the mathematical arguments on the behaviour of their expressions in terms of probability distributions, and analyzing the continuity and discontinuity of their graphical curves the global and local natures of the Shannon entropy and Fisher information, respectively, can be justified51. On the other hand, for Fisher information, Eq.(2), an equivalent expression ashas also been proposed45.It has been shown that although the two forms of the Fisher information are identical in value, the local behaviours of the respective densities are not.The GBP entropy has been resulted from the reformulation of the ground state density functional theory into a macroscopic local version of thermodynamics to describe the behaviour of microscopic electrons through introduction of the concept of local temperature. Finally, Onicescu information energy can be considered as a finer measure of dispersion distribution than Shannon information entropy and since it does not have the dimension of energy in the physical sense it is a purely statistical concept.
3 Computational details
The richness of stable local minima characterizing the potential energy surface (PES) of clusters makes their structural investigations as a challenging task. In such kinds of PESs, determination of the ground state is not an easy task. As one of these PESs, PES of water nanoclusters should be named where the definitive assignments to specific conformations were not always possible due to the presence of multiple isomers. As systems under study in the present work, we have considered 24 structural isomers of (H2O)6 nanocluster as a representative model52. To examine the effect of the size of nanoclusters on the extent of applicability of the information theory functionals, four different isomers of the water 32- and 64-mers, (H2O)32and (H2O)64, at the recommended geometries have also been included in our calculations53. For all the considered water nanoclusters, the corresponding wave functions and densities have been derived at the B3LYP/6-311++G(d,p) level of theory using the Gaussian 09 suite of programs.54On the used level of theory it is noted here that in previous efforts it has been shown that there is no visible dependence on the choice of basis sets and functional forms for steric and informational analyses of the systems21. Moreover, in another work15, it has also been pointed out that there is possibility for defining and computing the steric effects using the ab initio wave function-based approaches similar to the already proposed scheme in DFT. All the computations of the information theoretic functionals have been run in multifunctional wave function analyzer program developed by Lu and Chen55. Atomic units were used throughout.
4 Results and discussion
Shown in Fig.1 are the geometrical structures of various isomers of (H2O)6nanoclusters along with the reference relative electronic energy with respect to the most stable isomer (I)52. We can see that at least fifteenth structural isomers are located within 3 kcal·mol-1(1 kcal = 4.1868 kJ) of the most stable isomer. This in turn leads to a very complex PES for (H2O)6nanocluster. The corresponding correlations between the relative information theoretic quantities and the relative electronic energies with respect to the first isomer for the considered (H2O)6nanoclusters are displayed in Fig.2.
It can be seen from the figure that there are relationships between the relative steric energies computed using various information theory functionals and the reference relative electronic energies with the following order: F > S > O > GBP. The best correlation was found for a local measure of information theory, Fisher information (R2= 0.963). Moreover, the positive slope of the correlations indicates that a larger value of relative electronic energy corresponds to a more positive value of relative information theory functionals and thus to a larger steric effect. In other words, the more stable a water hexamer, the smaller its information theoretic functional which in turn suggests that for a lower energy structure, its steric repulsion should be smaller. On the other hand, in agreement with the minimum steric repulsion principle, since a lower steric repulsion implies smaller size, more stable clusters are often compact and small49.

Fig.1 Geometrical structures of the water hexamers under study.Colour conventions: black (oxygen) and light gray (hydrogen). The numbers below the structures are the CCSD(T) reference relative energies (kcal·mol-1) from Ref.52.
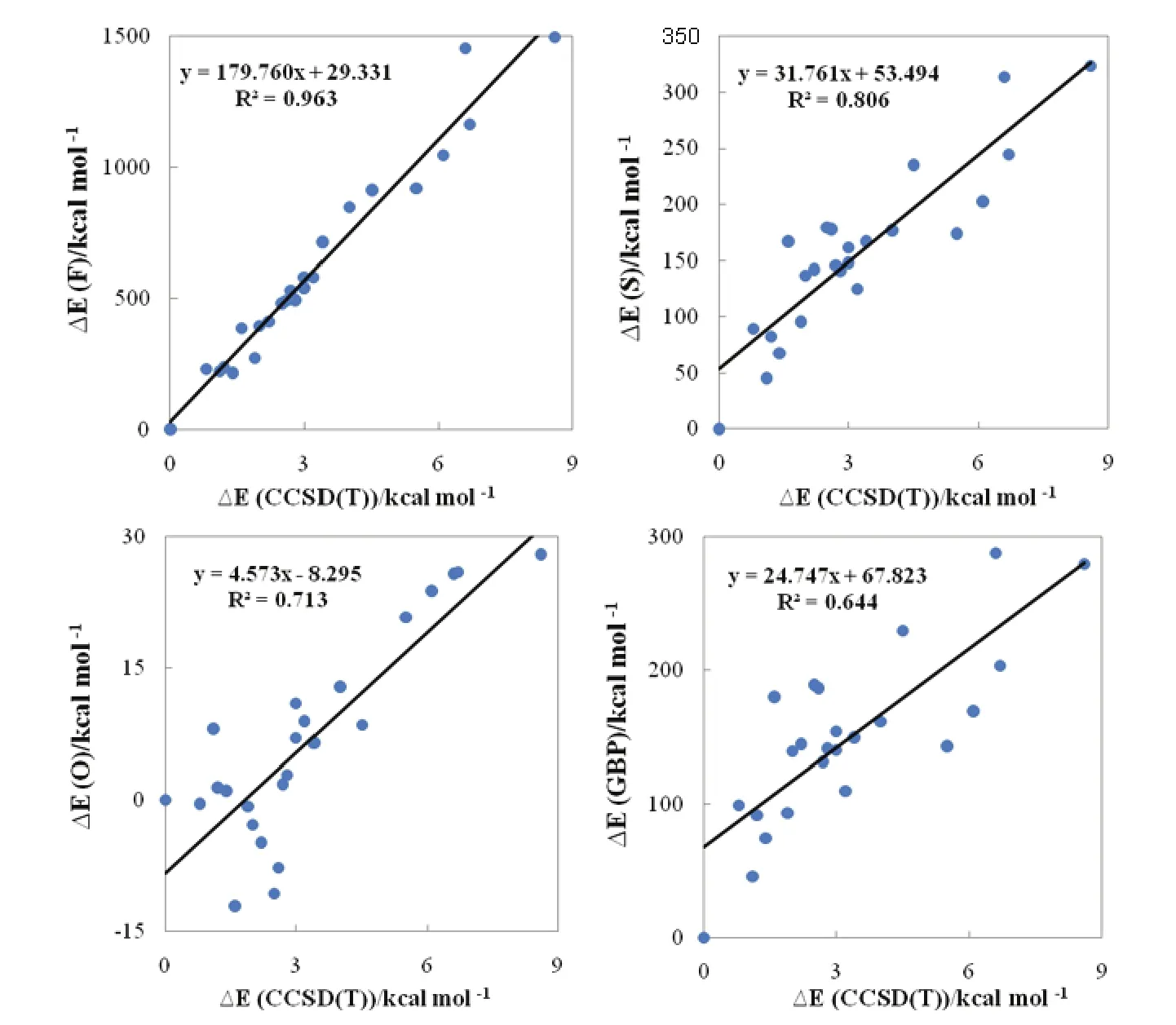
Fig.2 Correlations between the relative steric energies computed using various information theory functionals and the reference CCSD(T)relative electronic energies with respect to the most stable isomer for the considered water nanoclusters (H2O)6.
We plot in Fig.3 the local distributions of various information theory functionals under study for the isomers VI and XIV of (H2O)6nanoclusters as illustrative examples. Although the shape of the isomers preserves when employing each of the information theory functionals, their different steric contributions are discernible from the corresponding maps. We find from the figures that the local behavior of Fisher information, Onicescu information energy, and Ghosh-Berkowitz-Parr entropy are similar and substantially different from the local distribution of Shannon entropy. This in turn affects the predictability power of various information theory functionals for the steric effects. Moreover, in agreement with the energetic analysis of the two hexamers which shows more stability of isomer VI (1.6 kcal·mol-1) compared to isomer XIV (3.0 kcal·mol-1) with respect to the first isomer52, we found from our data that the steric contribution in the isomer VI of water hexamer is smaller than that provided for isomer XIV, indicating larger stability for the former isomer.
As demonstrated in recent related works56,57, simultaneous employing the information theoretic quantities together can generate a totally different outcome and more accurate description of the system. This is because these quantities are quantitative measures of different properties of the electron density distribution and show different scaling properties. However, there are numerous possible forms for considering more than one information theoretic quantity. For simplicity, in this work we have adopted the linear combination of these quantities aswhere P is the property under study (relative electronic energies),iQ are the information theoretic quantities of concern, andia are the coefficients to be determined by the least-squares fitting. The fitted formula as ΔE(CCSD(T)) = 0.605ΔE(F) + 35.855ΔE(S) + 14.224ΔE(O) - 28.195ΔE(GBP) + 0.216 was obtained. The regression coefficient for the correlation between the fitted relative energies from this formula and the reference values was found to be 0.980, larger than that provided from each information theoretic quantity individually. This in turn reveals that when the information theoretic quantities put together they can provide more accurate predictions of the order of stabilities in water nanoclusters. However, there is also other possibilities to extend this approach to different properties and using other forms to consider information theoretic quantities simultaneously (other than linear combination), whose result may be reported in future investigations. Lastly, these findings confirm again the proposal introduced by Liu et al.56, who proposed that when using a given known electron density to determine electronic properties of an electronic system, besides using the Kohn-Sham scheme of density functional theory as a conventional approach there is also an alternative route in which the functionals from information theory come into play.
Regarding the extent of accountability of the best information theory functional in our calculations, Fisher information, one might ask whether the obtained results from this measure are applicable to other sizes of the water nanoclusters as well. To answer this question we have also included a few structural isomers of large water nanoclusters (H2O)32and (H2O)64. The corresponding geometrical structures along with the reference relative electronic energy with respect to the first isomer as the most stable isomer are shown in Fig.4.
For (H2O)32, the relative values of Fisher information with respect to the most stable structure were found to be 432.5, 1119.3, and 7307.8 kcal·mol-1, and for (H2O)64 the corresponding values have been obtained as 5421.9, 6356.0, and 6985.0 kcal·mol-1, respectively. Concerning the values of the reference relative energies and these data we find that not only for small size nanoclusters but also for larger ones the Fisher information can well reproduce the relative order of stabilities. Needless to say that, for comprehensive conclusions in this context more analyses on various systems and water nanoclusters with large number of coordinated water molecules are needed58,59.
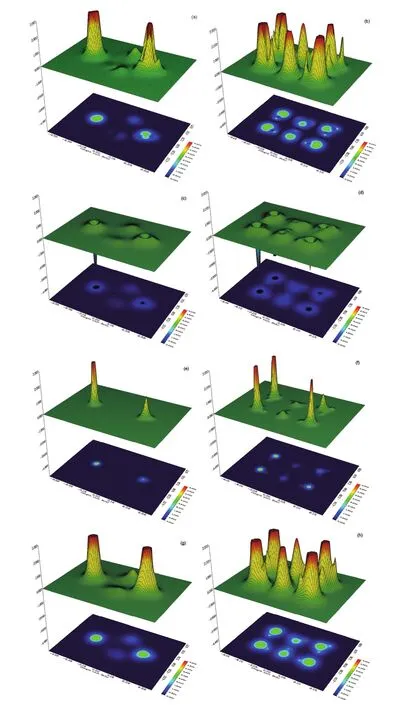
Fig.3 The local distributions of various information theory functionals for isomers VI (left panel) and XIV (right panel) of water hexamers.(a) and (b): Fisher information; (c) and (d): Shannon entropy; (e) and (f): Onicescu information energy; (g) and (h): Ghosh-Berkowitz-Parr entropy.

Fig.4 Geometrical structures of the water nanoclusters (H2O)32 and (H2O)64.Colour conventions: black (oxygen) and light gray (hydrogen). The numbers below the structures are the reference relative energies (kcal·mol-1) from Ref.53.
5 Final comments
In this work, the predictability power of information theory functionals like Fisher information, Shannon entropy, Onicescu information energy, and Ghosh-Berkowitz-Parr entropy has been assessed for the steric analysis of water nanoclusters. We have considered the structural isomers of water hexamers, 32-, and 64-mers as benchmarks and shown that there are relationships between the relative energies of water nanoclusters and the computed steric energies using the information theoretic quantities. From another perspective, the simultaneous consideration of the information theoretic quantities together was also taken into account, leading to more accurate descriptions of the order of stabilities in water nanoclusters. Lastly, the extent of applicability of information theoretic quantities to larger water nanoclusters with 32 and 64 units has also been analyzed. From the obtained data we found that although various information theoretic quantities may be useful for the present purpose, Fisher information has the best performance among other measures.
Acknowledgements: The author is grateful to Shiraz University for providing the needed computational facilities for the present project.
(1) Taft, R. W., Jr. Steric Effect in Organic Chemistry; Newman, M. S. Ed.; Wiley: New York, 1956.
(2) Hoffmann, R. J. Mol. Struct. (THEOCHEM) 1998, 1, 424. doi: 10.1016/S0166-1280(97)00219-4
(3) Ayers, P. W. J. Chem. Phys. 2000, 113, 10886. doi: 10.1063/1.1327268
(4) Parr, R. G.; Ayers, P. W.; Nalewajski, R. F. J. Phys. Chem. A 2005, 109, 3957. doi: 10.1021/jp0404596
(5) Ayers, P. W. Faraday Discuss. 2007, 135, 161. doi: 10.1039/B606877D
(6) Hohenberg, P.; Kohn, W. Phys. Rev. 1964, 136, B864. doi: 10.1103/PhysRev.136.B864
(7) Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, A1133. doi: 10.1103/PhysRev.140.A1133
(8) Parr, R. G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford: New York, 1989.
(9) Tsuneda, T. Density Functional Theory in Quantum Chemistry; Springer: New York, 2014.
(10) Liu, S. B. J. Chem. Phys. 2007, 126, 244103. doi: 10.1063/1.2747247
(11) von Weizs?cker, C. F. Z. Phys. 1935, 96, 431. doi: 10.1007/BF01337700
(12) Liu, S. B.; Govind, N.; Pedersen, L. G. J. Chem. Phys. 2008, 129, 094104. doi: 10.1063/1.2976767
(13) Torrent-Sucarrat, M.; Liu, S. B.; De Proft, F. J. Phys. Chem. A 2009, 113, 3698. doi: 10.1021/jp8096583
(14) Tsirelson, V. G.; Stash A. I.; Liu, S. B. J. Chem. Phys. 2010, 133, 114110. doi: 10.1063/1.3492377
(15) Esquivel, R. O.; Liu, S. B.; Angulo, J. C.; Dehesa, J. S.; Antolín, J.; Molina-Espíritu, M. J. Phys. Chem. A 2011, 115, 4406. doi: 10.1021/jp1095272
(16) Huang, Y.; Zhong, A.-G.; Yang, Q.; Liu, S. B. J. Chem. Phys. 2011, 134, 084103. doi: 10.1063/1.3555760
(17) Alipour, M.; Mohajeri, A. Mol. Phys. 2012, 110, 2895. doi: 10.1080/00268976.2012.679638
(18) Rinco?n, L.; Almeida, R. J. Phys. Chem. A 2012, 116, 7523. doi: 10.1021/jp300160g
(19) Alipour, M.; Mohajeri, A. J. Phys. Org. Chem. 2012, 25, 797. doi: 10.1002/poc.2921
(20) Liu, S. B. J. Phys. Chem. A 2013, 117, 962. doi: 10.1021/jp312521z
(21) Rong, C.; Lu, T.; Liu, S. B. J. Chem. Phys. 2014, 140, 024109. doi: 10.1063/1.4860969
(22) Alipour, M. Chem. Phys. 2014, 434, 11. doi: 10.1016/j.chemphys.2014.02.008
(23) Liu, S. B.; Schauer, C. K. J. Chem. Phys. 2015, 142, 054107. doi: 10.1063/1.4907365
(24) S. B. Liu, J. Phys. Chem. A 2015, 119, 3107. doi: 10.1021/acs.jpca.5b00443
(25) Wu, Z.; Rong, C.; Lu, T.; Ayers, P. W.; Liu, S. B. Phys. Chem.Chem. Phys. 2015, 17, 27052. doi: 10.1039/C5CP04442A
(26) Fisher, R. A. Proc. Cambridge Philols. Soc. 1925, 22, 700. doi: 10.1017/S0305004100009580
(27) Shannon, C. E. Bell Syst. Tech. J. 1948, 27, 379. doi: 10.1002/bltj.1948.27.issue-3
(28) Onicescu, O. C. R. Acad. Sci. Paris A 1966, 263, 25.
(29) Ghosh, S. K.; Berkowitz, M.; Parr, R. G. Proc. Natl. Acad. Sci. U. S. A. 1984, 81, 8028. doi: 10.1073/pnas.81.24.8028
(30) Parr, R. G.; Ayers P. W.; Nalewajski, R. F. J. Phys. Chem. A 2005, 109, 3957. doi: 10.1021/jp0404596
(31) Sen, K. D.; Katriel, J. J. Chem. Phys. 2006, 125, 074117. doi: 10.1063/1.2263710
(32) Ayers, P. W. Theor. Chem. Acc. 2006, 115, 370. doi: 10.1007/s00214-006-0121-5
(33) Nagy, á. Chem. Phys. Lett. 2007, 449, 212. doi: 10.1016/j.cplett.2007.10.026
(34) Borgoo, A.; Geerlings, P.; Sen, K. D. Phys. Lett. A 2008, 372, 5106. doi: 10.1016/j.physleta.2008.05.072
(35) Nagy á.; Liu, S. B. Phys. Lett. A 2008, 372, 1654. doi: 10.1016/j.physleta.2007.10.055
(36) Angulo, J. C.; Antolín, J. J. Chem. Phys. 2008, 128, 164109. doi: 10.1063/1.2907743
(37) Tsirelson, V. G.; Nagy, á. J. Phys. Chem. A 2009, 113, 9022. doi: 10.1021/jp904836j
(38) Nagy, á.; Romera, E. Chem. Phys. Lett. 2010, 490, 242. doi: 10.1016/j.cplett.2010.03.057
(39) Geerlings, P.; Borgoo, A. Phys. Chem. Chem. Phys. 2011, 13, 911. doi: 10.1039/C0CP01046D
(40) Alipour, M. Mol. Phys. 2013, 111, 3246. doi: 10.1080/00268976.2013.777814.
(41) Alipour, M. Chem. Phys. Lett. 2015, 635, 210. doi: 10.1016/j.cplett.2015.06.073
(42) Nagy, á. Int. J. Quantum Chem. 2015, 115, 1392. doi: 10.1002/qua.24812
(43) Esquivel, R. O.; Molina-Espíritu, M.; López-Rosa, S.; Soriano-Correa, C.; Barrientos-Salcedo, C.; Kohout, M.; Dehesa, J. S. ChemPhysChem 2015, 16, 2571. doi: 10.1002/cphc.201500282
(44) Delle Site, L. Int. J. Quantum Chem. 2015, 115, 1396. doi: 10.1002/qua.24823
(45) Liu, S. B. J. Chem. Phys. 2007, 126, 191107. doi: 10.1063/1.2741244
(46) Alipour, M.; Mohajeri, A. Mol. Phys. 2012, 110, 403. doi: 10.1080/00268976.2011.649795
(47) Liu, S. B. Acta Phys. -Chim. Sin. 2016, 32, 98. doi: 10.3866/PKU.WHXB201510302
(48) Alipour, M.; Safari, Z. Phys. Chem. Chem. Phys. 2016, 18, 17917. doi: 10.1039/C6CP02750D
(49) Wang, Y. J.; Zhao, D. B.; Rong, C. Y.; Liu, S. B. Acta Phys.-Chim. Sin. 2013, 29, 2173. doi: 10.3866/PKU.WHXB201308272
(50) Alipour, M. Chem. Phys. 2014, 434, 11. doi: 10.1016/j.chemphys.2014.02.008
(51) Frieden, B. R. Physics from Fisher Information; Cambridge University Press: Cambridge, 1998.
(52) Hincapié, G.; Acelas, N.; Casta?o, M.; David, J.; Restrepo, A. J. Phys. Chem. A 2010, 114, 7809. doi: 10.1021/jp103683m
(53) Yuan, D.; Li, Y.; Ni, Z.; Pulay, P.; Li, W.; Li, S. J. Chem.Theory Comput. 2017, 13, 2696. doi: 10.1021/acs.jctc.7b00284
(54) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; et al., Gaussian 09, Revision B.01; Gaussian Inc.: Wallingford, CT, 2010.
(55) Lu, T.; Chen, F. J. Comput. Chem. 2012, 33, 580. doi: 10.1002/jcc.v33.5
(56) Zhou, X. Y.; Rong, C.; Lu, T.; Zhou, P.; Liu, S. B. J. Phys.Chem. A 2016, 120, 3634. doi: 10.1021/acs.jpca.6b01197
(57) Zhou, X.; Yu, D.; Rong, C.; Lu, T.; Liu, S. B. Chem. Phys.Lett. 2017, 684, 97. doi: 10.1021/acs.jpca.6b01197
(58) Maroulis, G. J. Chem. Phys. 2000, 113, 1813. doi: 10.1063/1.481985
(59) Maroulis, G. Int. J. Quantum Chem. 2012, 112, 2231. doi: 10.1002/qua.23186

