Effects of a Weakly Interacting Light U Boson on Protoneutron Stars Including the Hyperon-Hyperon Interactions?
Zi Yu(喻孜),Yan Xu(許妍), Gui-Qing Zhang(張貴清),and Tao-Ping Hu(胡濤平)
1College of Science,Nanjing Forestry University,Nanjing 210037,China
2Changchun Observatory,National Astronomical Observatories,Chinese Academy of Sciences,Changchun 130117,China
3Department of Physics,Tianjin University of Science and Technology,Tianjin 300457,China
1 Introduction
A weakly interacting light U-boson[1]was used as the interaction propagator of the MeV dark matter and was used to account for the bright 511 keV-ray from the galactic bulge.[2?6]The U-boson is thought to be a favorite candidate to describe the violating of gravity.Gravity is the first force discovered in nature.However,it is still the most poorly characterized,compared to three other fundamental forces that can be favorably unified within the gauge theory.For the further grand unification of four forces,the inverse-square-law(ISL)of gravity is expected to be violated.Deviations from the ISL may be parameterized in terms of the exchanges by the U-boson.To constrain the characteristic scale of the U-boson,the related laboratory experiments are needed.So far,constraints on the deviations from the ISL have been set experimentally in the sub-millimeter scale[7?12]and down to distances~10 fm where effects of light bosons of extensions of the standard model can be expected.[13?17]Constraints on the coupling constants from unobserved missing energy decay modes of ordinary mesons are discussed in Ref.[18].The U boson can escape detection in most laboratory experiments due to its small couplings.However,the U boson interacting with baryons can modify the equation of state(EOS)of nuclear matter.This means the U-boson may influence the structure of neutron stars.Neutron stars are thus a natural testing ground of the U boson.
The global properties of the neutron star are sensitive to the EOS of dense matter.In the year of 2009,an abnormal EOS with a possible super-soft symmetry energy[19?20]was found by analyzing the FOPI/GSI data on the π+/π?radio in relativistic heavy-ion collisions.[21]This finding can result in many consequences,while a direct challenge is how to stabilize a normal neutron star with the super-soft symmetry energy.To solve this problem,one can consider the contribution of the U-boson.When the U-boson is taken into account,a neutron star,even with the super-soft symmetry energy,can be stable.[22]In the year of 2010,using the general relativistic Shapiro delay,the mass of PSR J1614-2230 was precisely measured to be 1.97±0.04M⊙,[23]making it the new holder of the maximum mass of neutron stars.This finding means the EOS of star matter should be very stiff.The hyperons were excluded as suggested in Ref.[23]since the EOS with hyperons seems too soft.However,as argued in some researches,[24?25]the EOS with hyperons in some models can be still very stiff.So the hyperons can not be excluded in large-mass neutron stars.In another way,one can also consider the contribution of the U boson since the U boson can stiffen the EOS.PSR J1614-2230 may include hyperons when the U boson is included.[26]In fact,with the inclusion of the U boson,the maximum mass of neutron stars can not rule out any soft EOS even if the hadron-quark phase transition appears.[27]At present,many researchers have studied the effects of the U boson on the neutron star.[26?29]
A protoneutron star is formed in the aftermath of the gravitational collapse of the core of a massive star.Neutrinos produced by the electron capture process are trapped in the star due to their short mean free path.[30]Therefore,a protoneutron star has rich leptons.This is different from the neutron star in which the neutrinos have run away.An interesting issue is that how the U-boson influences the star with rich leptons.The research is still scarce.[31]On the other hand,a protoneutron star is a highly compact object.At high densities,hyperons can appear in the stars.The hyperon-hyperon(YY)interaction should be play an important role.There are two ways to describe the YY interactions now.One is the strong YY interaction deduced from the early experiments[32?34](?BΛΛ~ 5 MeV).The other is the weak YY interaction deduced from the later observation of the double-Λ hypernucleus[35](?BΛΛ~ 1 MeV).Either one of these two YY interactions has remarkable effects on the structure of neutron star matter.[36?45]It is expected that the YY interactions should play an important role in protoneutron star matter.Up to now,the YY interactions have always not been included in the researches on protoneutron star matter.Consequently,we do not know how the U-boson affects the properties of the protoneutron stars with the inclusion of the YY interactions.This article aims to answer this question in the framework of the relativistic mean field theory(RMFT).[46?47]In addition,the effects of the U-boson on the protoneutron star in two cases of the YY interactions will be compared.The possible way to constrain the U-boson will be discussed.
2 The Theory Model
In the standard RMFT,the Lagrangian density of protoneutron star matter is,
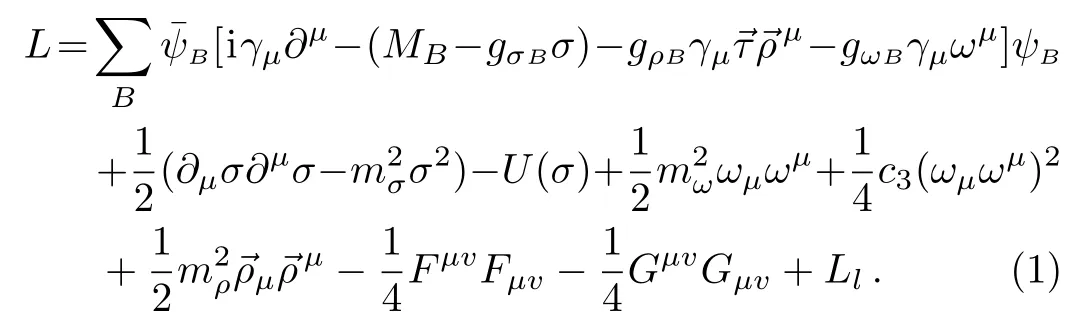
Nevertheless,the standard RMFT is not able to reproduce the observed strongly attractive ΛΛ interaction.The situation can be remedied by introducing two additional meson fields,namely,the scalar meson σ?(975)and the vector meson ? (1020).[48?49]The additional Lagrangian,which can reproduce the hyperon-hyperon interactions has the form of,


where σ?and ? are only coupled to hyperons.
In protoneutron stars,chemical equilibrium among the baryons and leptons implies the relation,
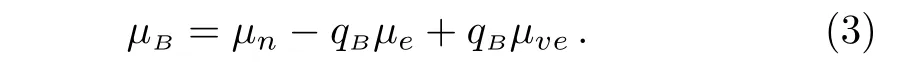
Electrical neutrality requires
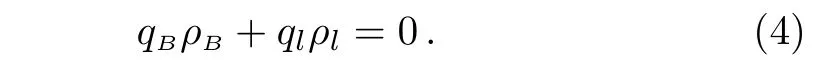
qBand qlstand for the electric charge of the baryon B and lepton l.Gravitational collapse calculations of the iron core of massive stars indicate that,the electron lepton number is Yl~0.4 in neutrino-trapped matter.[50]In this case,the fraction of muons are very small compared to that of electrons especially when the hyperons are present.[51]The effects of the muons on the EOS would be moderate.So the muons are not included in this article and Yμ=0 is imposed for convenience.The lepton fraction of protoneutron star matter can be defined as,

In the mean field approximation,the motion of field equations for mesons are,

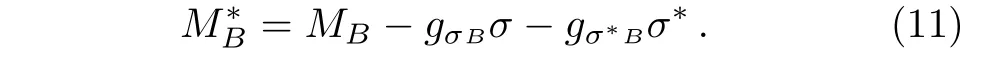
The chemical potentialμBhas the form of,
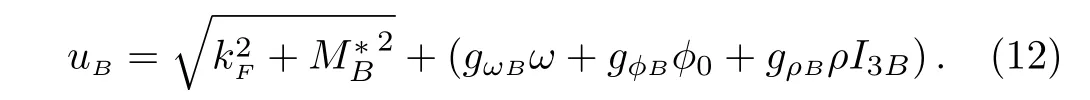
The pressure and energy density in the high-density range have the forms of,
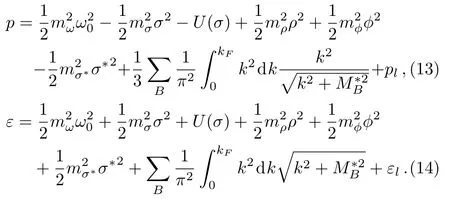
pland εlstand for the contributions from leptons.
The deviation from the ISL of gravity is always characterized by adding a Yukawa term to the normal gravitational potential,

where α is a dimensionless strength parameter, λ is the length scale and G∞is the universal gravitational constant. In the boson exchange picture,α=±g2/(4πG∞M2B)and λ =1/μ.The g2,μ,and MBare coupling constant of the U boson with baryons,the U boson and baryon mass,respectively.The effect of the U boson on the energy density of nuclear matter can be evaluated by averaging the corresponding Yukawa potential,
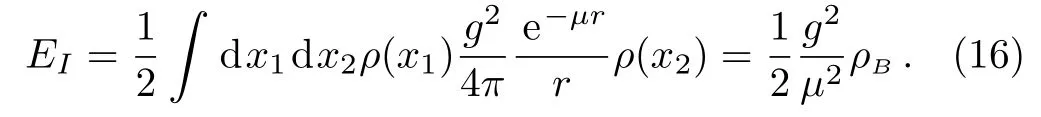
A flavor-singlet vector boson gives equal contributions to the chemical potentials of the octet baryons and does not violate the chemical β-equilibrium.[29]In this article,the U boson is assumed to be a flavor-singlet vector boson.
In the calculation,the TM1[52]set is used(see Table 1).The hyperon couplings are not relevant to the ground state of properties of nuclear matter but information about them can be gathered from levels in hypernuclei.Hence,one can use SU(6)symmetry for the vector coupling constants
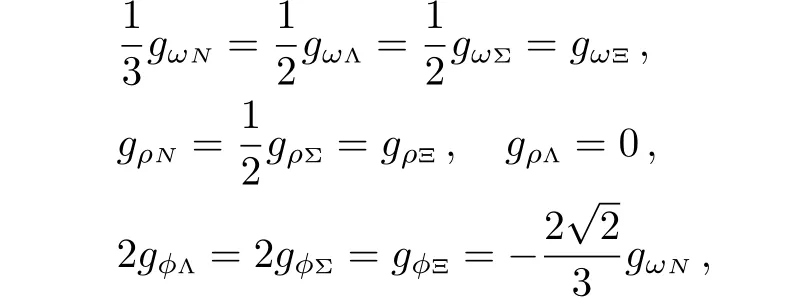
and fix the scalar coupling constants to the potential depth of the corresponding hyperon in normal nuclear matter.Following Refs.[53–55],we choose,

to determine the scalar coupling constants gσΛ,gσΣand gσΞ.For gσ?Λ,gσ?Σand gσ?Ξ,we consider two cases of the YY interactions.The strong YY interactions deduced from the earlier measurement[32?34]suggests that,
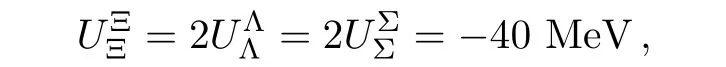
while the weak YY interaction implied by the later measurement[35]suggests that,

The scalar coupling constants for the hyperons are shown in Table 2.With the above coupling cets,the coupled equations can be solved self-consistently.Then,the global properties of the protoneutron star are obtained.

Table 1 The TM1 set.

Table 2 The hyperon scalar coupling constants.
3 Numerical Results
The particle fractions Yi= ρi/ρBas a function of the baryon density in two cases of the YY interactions are shown in Fig.1.When the Fermi energy of nucleons exceeds the rest mass of hyperons,the conversion from nucleons to hyperons is energetically favorable.As the density increases,the Λ, Ξ and Σ hyperons appear one by one.With the weak(strong)YY interaction,the threshold densities for Λ,Ξ?and Ξ0are 0.38(0.38)fm?3,0.69(0.64)fm?3and 0.88(0.77)fm?3,respectively.The Σ?,Σ0,Σ+with the strong YY interaction begins to appear at 1.13 fm?3,1.16 fm?3,1.19 fm?3,respectively,whereas they do not appear in protoneutron star matter with the weak YY interaction.The strong YY interaction supplies stronger additional attractive interactions for hyperons than the weak YY interaction.Consequently,the strong YY interaction favours earlier onsets of Ξ?and Ξ0hyperons and leads to larger fraction of hyperons than the weak YY interaction at high densities.The fraction of electrons is the same as that of the protons at low densities due to the electrical neutrality.They become different after the onset of the new charged specie of the Ξ?hyperon.The trapped neutrinos distinguish a protoneutron star from a normal neutron star.For the fixed value of YL=0.4,the neutrino fraction changes with the density in a different trend from the electron fraction.It is shown in Fig.1 the fraction of neutrinos decreases with the density at first and then increases.The appearance of hyperons rises the abundance of neutrinos.This phenomenon can be understood by the inherent relation between hyperons and electrons.For this reason,the weak YY interaction,calculated with which the abundance of hyperons is smaller,leads to less amount of neutrinos than the strong YY interaction at high densities.
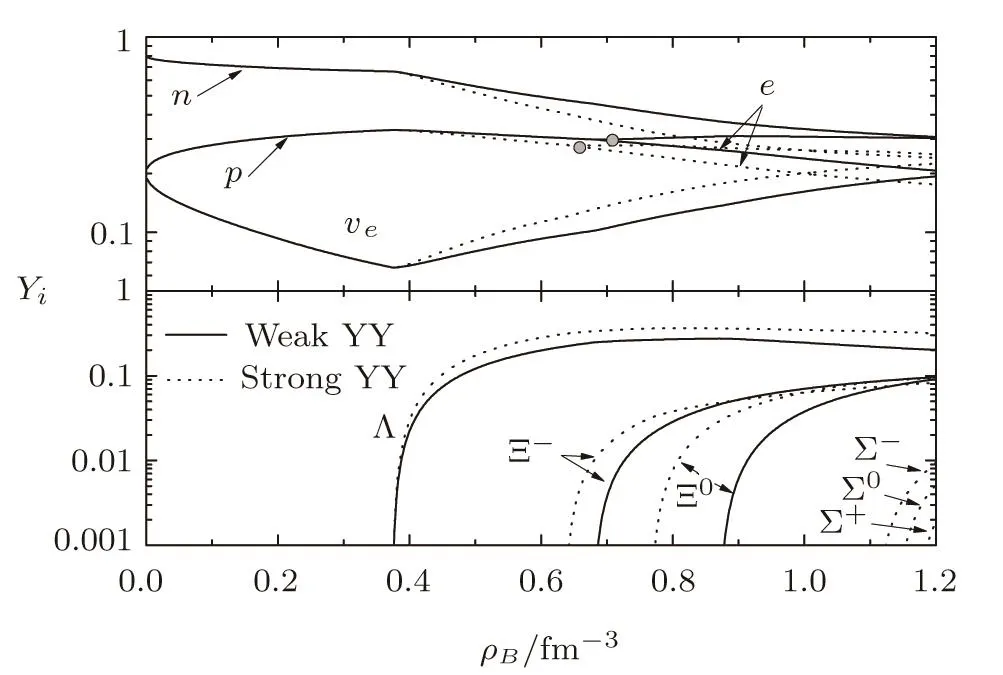
Fig.1 The particle fraction Yi= ρi/ρBas a function of the baryon density in protoneutron star matter.The critical positions where the curves for the electron and the proton start to separate are marked as gray circles.
Figure 2 shows the EOS of protoneutron star matter for a set of values of U-boson constant(g2/μ2).The abundance of hyperons with the strong YY interaction is larger than that with the weak YY interaction as shown in Fig.1.Therefore,the EOS with the strong YY interaction is softer than that with the weak YY interaction.In the RMFT approximation,the contribution of the U-boson has the form of a vector meson,which provides the additional repulsive interaction besides ω meson.Consequently,the U-boson stiffens the EOS.It is noticed that the effects of the U-boson on the EOS in two cases of the YY interactions have some differences.The EOS with the strong YY interaction acquires a more apparent stiffening than that with the weak YY interaction by including the U-boson.It can be seen from Fig.2,as g2/μ2increases,the curves in two cases of the YY interactions become closer and closer to each other.The reason is as follows.Compared to the standard model with the σ-ω-ρ mesons,the model with the YY interaction introduces two additional mesons of σ?and ?,which supply the additional attractive and repulsive interactions,respectively.Their contributions in the pressure are the opposite as shown in Eq.(13).If the subtraction of the repulsion and attraction in the pressure,namely,the value of the expression of(see Eq.(13)),is smaller,the role of the U-boson in modifying the pressure will be more important.The model with the strong YY interaction provides much stronger attraction from the σ?-meson than that with the weak YY interaction,while the repulsive interactions from the ?-meson in two models are close to each other.The?V with the strong YY interaction is smaller in the pressure.The modification to the pressure by the U-boson with the strong YY interaction is more significant(shown in the inner panel in Fig.2).The contribution of the σ?and ? mesons in the energy density are both positive as shown in Eq.(14).The U-boson plays a relatively marginal role in changing the energy density.Therefore,the U-boson can modify the correlation between the pressure and energy density more obviously in the model with softer EOS.
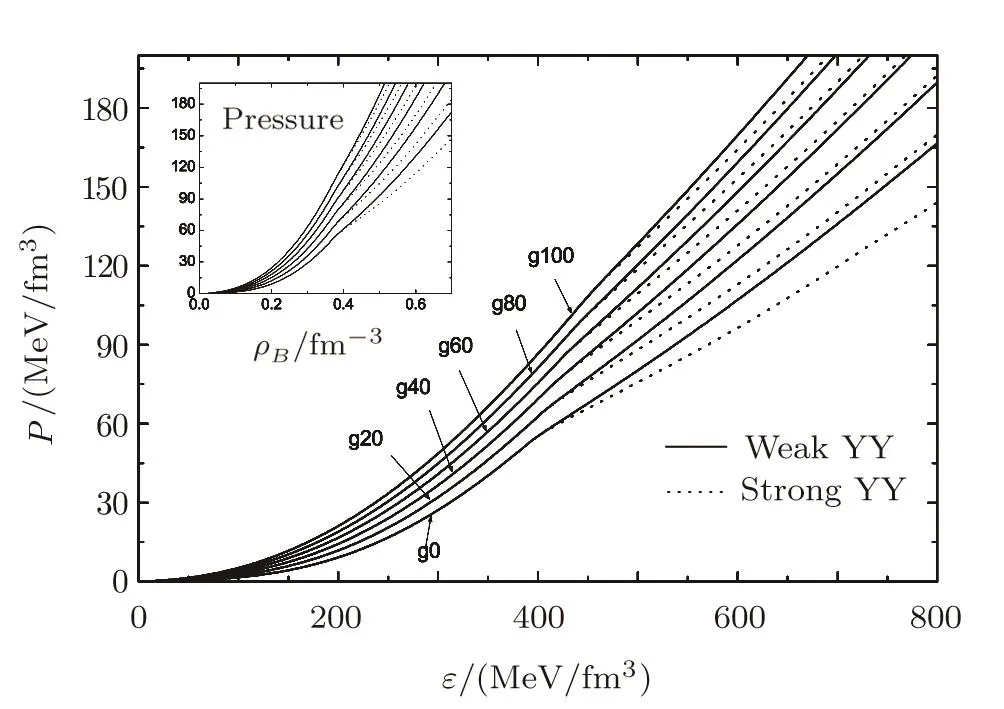
Fig.2 The EOS of protoneutron star matter.The inner panel shows the pressure as a function of the baryon density.gχstands for the U-boson contribution with g2/μ2= χ GeV?2.
The mass-radius relations calculated with two types of the YY interactions is shown in Fig.3.The U-boson leads to the rise of the maximum mass.As g2/μ2increases from 0 to 100 GeV?2,the maximum mass with the weak YY(strong YY)interaction increases from 1.92(1.82)M⊙to 2.66(2.65)M⊙,the increment reaching 39%(46%).The maximum mass with the strong YY interaction is more sensitive to the coupling strength of the U-boson than that with the weak YY interaction.This is due to the U-boson-induced modification to the EOS in two cases of the YY interactions as shown in Fig.2.It is interesting to compare the modification to the maximum mass by the U-boson in the protoneutron star with that in the neutron star.Thus,the maximum mass of neutron star is calculated in the same range of g2/μ2=0~ 100 GeV?2,which is shown in the inner panel in Fig.3.As g2/μ2increases from 0 to 100 GeV?2,the maximum mass of the neutron star with the weak YY(strong YY)interaction increases from 1.75(1.56)M⊙to 2.71(2.69)M⊙,the increment reaching 55%(72%).The maximum mass of the neutron star acquires a larger increment than that of the protoneutron star.The phenomenon can be understood as follows.There are rich leptons in the protoneutron star.The rich leptons prevent the produces of the hyperons.The small abundance of hyperons leads to a stiffEOS,which weakens the effect of the U-boson.Therefore,compared to the maximum mass of the neutron star,that of the protoneutron star is less sensitive to the U-boson.In addition to the rise of the star maximum mass,the U-boson also yields a very apparent expansion of the star size as shown in Fig.3.
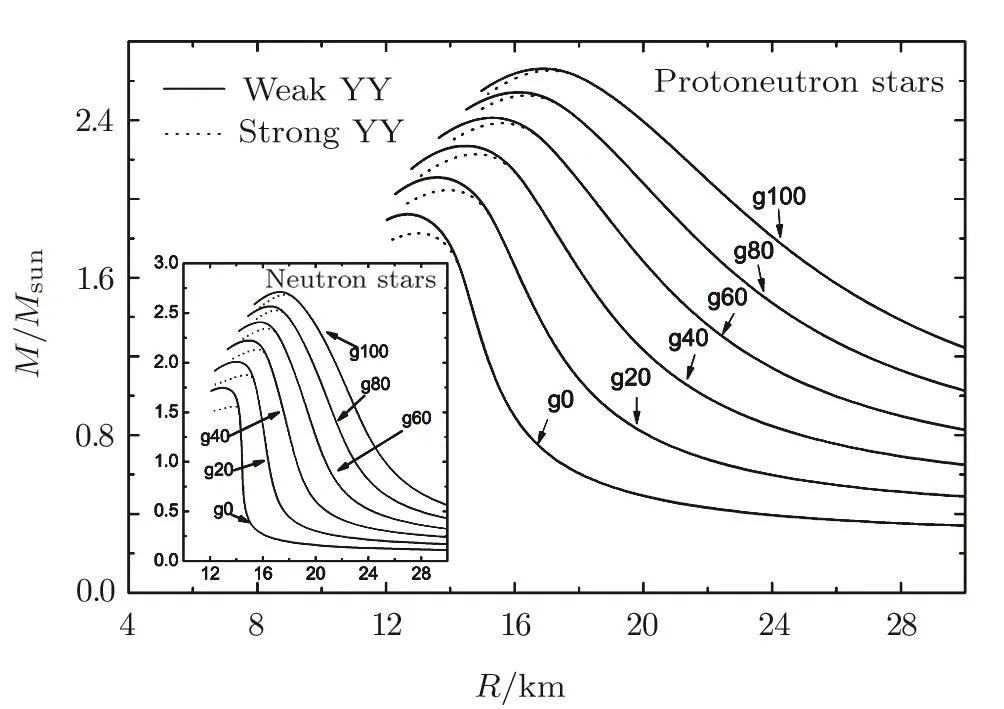
Fig.3 The mass-radius relations of the protoneutron stars calculated with the weak YY and strong YY interaction.The inner panel is the mass-radius relations of the neutron stars for the comparison.gχstands for the U-boson contribution with g2/μ2=χ GeV?2.
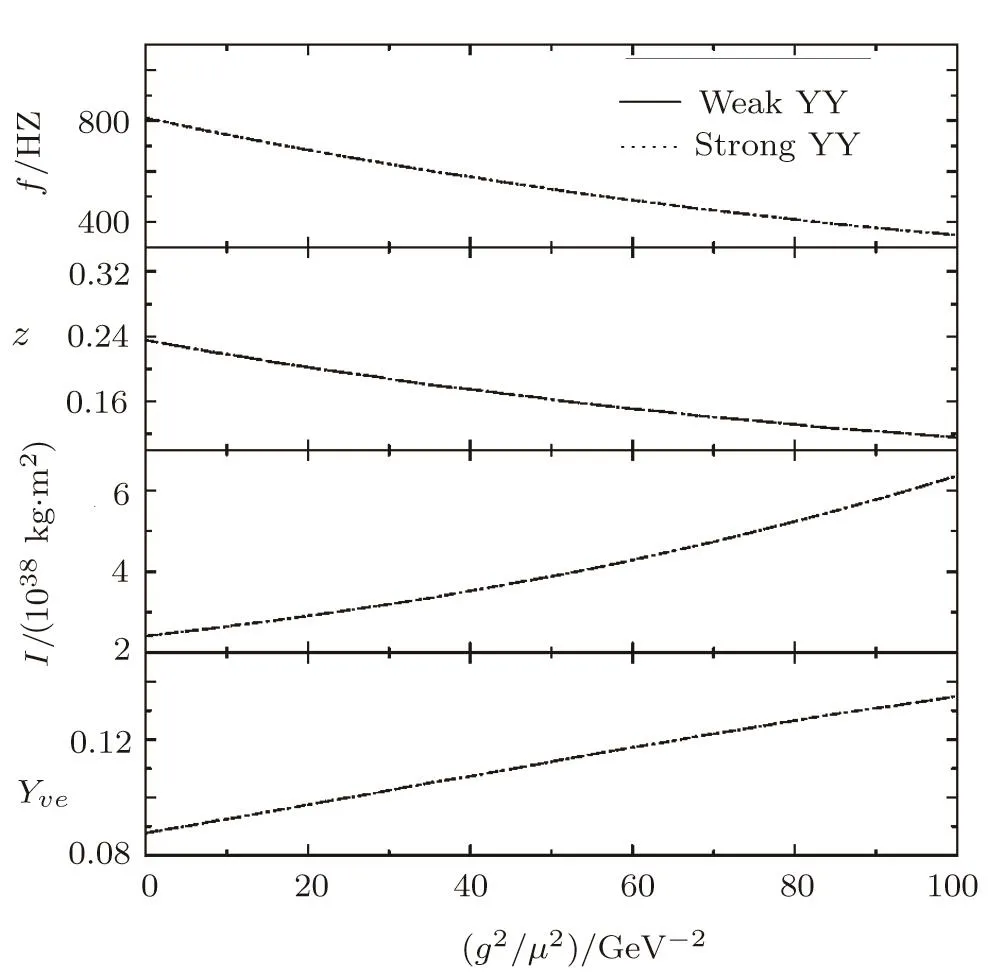
The non-nucleon degree of freedom in stellar matter is always an important topic.Whether the hyperons can appear in the neutron star used to cause some controversy.[23,56?57]The article will examine this issue in the case of the protoneutron star.For this purpose,the central density corresponding to the maximum mass is drawn in the top panel in Fig.4.The central density corresponding to the maximum mass is the maximum central density for stable protoneutron stars.One specie of hyperon can appear in a stable protoneutron star only when its critical density is smaller than the maximum central density.As g2/μ2increases from 0 to 100 GeV?2,the maximum central density with the weak YY(strong YY)decreases from 0.86(0.82)fm?3to 0.52(0.51)fm?3.If the maximum central density becomes lower than the critical density for one specie of hyperon,this hyperon cannot appear in any stable protoneutron star.Λ begins to appear in protoneutron star matter at densities higher than 0.38 fm?3in both two cases of the YY interactions.The maximum central density of the protoneutron star is higher than 0.38 fm?3.Therefore,the protoneutron star can contain Λ. Ξ?begins to appear when the density exceeds 0.69(0.64)fm?3with the weak(strong)YY interaction.As the coupling strength of the U-boson increases,the maximum central density will decrease to the values below 0.69(0.64)fm?3.Then,the protoneutron star can not contain Ξ?.When g2/μ2exceeds 36(44)GeV?2,Ξ?can not appear in the protoneutron star with the weak(strong)YY interaction.Ξ0begins to appear when the density exceeds 0.88(0.77)fm?3with the weak(strong)YY interaction.With the weak YY interaction,the protoneutron star can not contain Ξ0.With the strong YY interaction,the protoneutron star can not contain Ξ0when g2/μ2exceeds 8 GeV?2.The thresholds for these hyperons are marked as black circles in Fig.4.In both middle and bottom panels of Fig.4,two curves are drawn.Upper curve represents the maximum mass(Mmax)while lower curve represents the threshold mass(Mth)corresponding to the central density ρc=0.38 fm?3(the critical value for the appearance of Λ hyperon).The mass of a hyperonized protoneutron star should satisfy the condition of Mth Fig.4 The top panel shows the central density corresponding to the maximum mass as a function of the coupling sets of the U-boson.The thresholds for the values of g2/μ2,exceeding which the hyperon can not appear in the star was marked as dark circles.The middle and bottom panels show the mass window for the hyperonized protoneutron stars with the weak YY interaction and the strong YY interaction,respectively.The species of hyperons,which can appear in the star are labeled in the region between two curves.The vertical lines for the boundary are drawn. To find out possible way to constrain the U-boson,the dependence of the star global properties on g2/μ2will be discussed in the following.PSR J1903-0327 has a mass of 1.67±0.02M⊙.[58]Using the mass of PSR J1903-0327,the global properties in the whole range of g2/μ2=0–100 GeV?2can be given.Figure 5 shows four types of the global properties of PSR J1903-0327 as a function of the coupling strength of the U-boson.In this article,the rotation frequency is estimated by following the work in Ref.[59] The momentum of inertia can be well approximated as[61] The total neutrino fraction is defined as, where Nveand NBstand for the total number of the neutrinos and baryons in the protoneutron star,respectively.The values of f,z,and I depend on the mass-radius relations according to the above equations.For a mass of 1.67 M⊙,the mass-radius relations with two different YY interactions are the same as shown in Fig.3.So with two different YY interactions,f,z and I are nearly the same.In the calculation,it is found that the central density of PSR J1903-0327 with the weak(strong)YY interaction changes from 0.43(0.45)to 0.15(0.15)fm?3,corresponding to g2/μ2changing from 0 to 100 GeV?2.At these low densities,the difference of the neutrino fraction in two cases of the YY interactions is very small as shown in Fig.1.Hence,the total neutrino fractions with two types of the YY interactions are also the same. Fig.5 The global properties of PSR J1903-0327 with 1.67M⊙ as a function of the values of g2/μ2. It can be seen from Fig.5 the curves for different cases of the YY interactions coincide.As g2/μ2increases from 0 to 100 GeV?2,the rotation frequency decreases from 811 HZ to 348 HZ,the decrement reaching 57%;the red shift decreases from 0.24 to 0.12,the decrement reaching 50%;the momentum of inertia increases from 2.4×1038kg·m2to 6.4×1038kg·m2,the increment reaching 167%.The effect of the U-boson on these properties are remarkable.It points out the importance of measuring the rotation frequency,the red shift and the momentum of inertia accurately for further constraint on the U-boson.The total neutrino fraction of PSR J1903-0327 is also sensitive to the U-boson as shown in the bottom panel of Fig.5.As g2/μ2increases from 0 to 100 GeV?2,the total neutrino fraction of PSR J1903-0327 increases from 9%to 13%,the increment reaching 44%.This will have implications in the cooling of the protoneutron star,since the amount of neutrinos defines whether the star decays into a low mass black hole or into a neutron star.In addition,it is very interesting to find that the curves for four types of the global properties are approximate straight-lines.The four global properties of PSR J1903-0327 change with g2/μ2in an approximate linear trend. This article investigates the effects of the U-boson on the properties of the protoneutron stars with the inclusion of the YY interactions.Using different YY interactions,the attractive interactions between hyperons are different in stellar matter.This directly leads to some consequences.The weak YY interaction results in later onsets of the Ξ?and Ξ0in protoneutron star matter than the strong YY interaction.It also leads to smaller abundance of the hyperons while larger fraction of neutrinos at high densities than the strong YY interaction.Calculated with the weak YY interaction,a stiffer EOS will be get.The maximum mass with the weak YY interaction is therefore larger than that with the strong YY interaction.When the U-boson is included,the properties of the protonturon star with two types of the YY interactions are both remarkably changed.As g2/μ2increases,the maximum mass increases while the central density corresponding to the maximum mass decreases.The species of hyperons,which can appear in a stable protoenturon star decreases when g2/μ2becomes high.The U-boson narrows down the mass window for a hyperonized protoneutron star.The rotation frequency,the red shift,the momentum of inertia and the total neutrino fraction of PSR J1903-0327 are sensitive to the U-boson.The four kinds of properties change with g2/μ2in an approximate linear trend.In addition to the modification to these four kinds of properties,the U-boson also increases the star radius remarkably.In this article,the possible in-medium effects of the U-boson have not been included.It is noticed that by considering the exchange of the weakly interacting light U-boson with appropriate in-medium parameters,the star radius can attain larger reduction,can even lie in the range of R<10 KM.[62?63]At present,there would be a few constraints on the radius though the star radius is still far o ffcertain.However,few models can predict so small radius,namely,R<10 KM.Therefore,if so small radius is established by the observation in the future,the U-boson as well as its in-medium effects will become very important.Of course,the validity of this should be eventually tested by more precise measurements of neutron star radii. This article also compares the sensitive roles of the U-boson under different conditions.The EOS with the strong YY interaction will acquire a more apparent stiffening by the U-boson than that with the weak YY interaction.Consequently,the maximum mass with the strong YY interaction is more sensitive to the U-boson.The U-boson also leads to a larger increase of the maximum mass for the neutron star than for the protoneutron star.Including the U-boson,the protoneutron star with the strong YY interaction is more likely able to contain multi specie of hyperons than that with the week YY interaction. To constrain the values of U-boson has been a longstanding goal of many terrestrial experiments and astrophysical observations. Here,the coupling constant we used is g2/μ2,which is equivalent to the|α|λ2. The recent experimental constraints on g2/μ2can be found in Ref.[29].To stabilize a neutron star using the EOS with super-soft symmetry energy,[19?20]the ratio g2/μ2–100 GeV?2was found to be needed.[22]In this work,the effect of the U-boson is investigated within the range of g2/μ2=0–100 GeV?2.This range can be consistent with constrains from the terrestrial experiments.For further constrains,one may turn to the effects of the U-boson on protoneutron stars.Calculated with g2/μ2=0–100 GeV?2,the U-boson is found to be able to affect the global properties of the protoneutron star remarkably.In particular,this work firstly found that the amount of neutrinos in the protoneutron star is very sensitive to the coupling constants of the U-boson.The amount of neutrinos is significant for the evolution of a protoneutron star.Therefore,accurate measurements of the star global properties as well as observations on the evolution of the protoneutron star should be helpful for further constraining the U-boson and studying the non-Newtonian gravity. [1]P.Fayet,Phys.Lett.B 95(1980)285 [2]C.Boehm,D.Hooper,J.Silk,et al.,Phys.Rev.Lett.92(2004)101301. [3]C.Boehm and P.Fayet,Nucl.Phys.B 683(2004)219. [4]E.G.Adelberger,B.R.Heckel,and A.E.Nelson,Annu.Rev.Nucl.Phys.Sci.53(2003)77. [5]M.Reece and L.T.Wang,J.High Energy Phys.07(2009)051. [6]P.Jean,J.Kn?dlseder,V.Lonjou,et al.,Astron.Astrophys.407(2003)L55;J.Kn?dlseder,V.Lonjou,P.Jean,et al.,Astron.Astrophys.411(2003)L457. [7]D.J.Kapner,T.S.Cook,E.G.Adelberger,et al.,Phys.Rev.Lett.98(2007)021101. [8]A.A.Geraci,S.J.Smullin,D.M.Weld,et al.,Phys.Rev.D 78(2008)022002. [9]S.K.Lamoreaux,Phys.Rev.Lett.78(1997)5. [10]R.S.Decca,D.L′opez,H.B.Chan,et al.,Phys.Rev.Lett.94(2005)240401. [11]V.M.Mostepanenko,R.S.Decca,E.Fischbach,et al.,J.Phys.A 41(2008)164054. [12]M.Bordag,V.M.Mostepanenko,and I.Y.Sokolov,Phys.Lett.A 187(1994)35. [13]R.Barbieri and T.E.O.Ericson,Phys.Lett.B 57(1975)270. [14]V.V.Nesvizhevsky and K.V.Protasov,Class.Quantum Grav.21(2004)4557. [15]Yu.N.Pokotilovski,Phys.Atom.Nucl.69(2006)924. [16]V.V.Nesvizhevsky,G.Pignol,and K.V.Protasov,Phys.Rev.D 77(2008)034020. [17]Y.Kamyshkov,J.Tithof,and M.Vysotsky,Phys.Rev.D 78(2008)114029. [18]P.Fayet,Phys.Rev.D 75(2007)115017. [19]Z.G.Xiao,B.A.Li,L.W.Chen,et al.,Phys.Rev.Lett.102(2009)062502. [20]Z.Q.Feng and G.M.Jin,Phys.Lett.B 683(2010)140. [21]W.Reisdorf,M.Stockmeier,A.Andronic,et al.,Nucl.Phys.A 781(2007)459. [22]D.H.Wen,B.A.Li,and L.W.Chen,Phys.Rev.Lett.103(2009)211102. [23]P.B.Demorest,T.Pennucci,S.M.Ransom,et al.,Nature(London)467(2010)1081. [24]I.Bednarek,P.Haensel,J.L.Zdunik,et al.,Astron.Astrophys.543(2012)A157 [25]W.Z.Jiang,B.A.Li,and L.W.Chen,Astrophys.J.756(2012)56 [26]Z.Yu,W.B.Ding,Tmurbagan Bao,et al.,Chin.Phys.Lett.28(2011)089701. [27]D.H.Wen,B.A.Li,L.W.Chen,et al.,arXiv:astroph.SR/1101.1504. [28]D.R.Zhang,P.L.Yin,W.Wei,et al.,Phys.Rev.C 83(2011)035801. [29]M.I.Krivoruchenko,F.S.imkovic,and A.Faessler,Phys.Rev.D 79(2009)125023. [30]A.Burrows,J.Hayes,and B.A.Fryxell,Astrophys.J.450(1995)830. [31]B.Hong,H.Y.Jia,X.L.Mu,et al.,Chin.Phys.C 6(2016)35. [32]M.Danysz,K.Garbowska,J.Pniewski,et al.,Nucl.Phys.49(1963)121;R.H.Dalitz,D.H.Davis,P.H.Fowler,et al.,Proc.R.Soc.A 426(1989)1. [33]D.J.Prowse,Phys.Rev.Lett.17(1966)782. [34]S.Aoki,S.Y.Bahk,K.S.Chung,et al.,Prog.Theor.Phys.85(1991)1287. [35]H.Takahashi,J.K.Ahn,H.Akikawa,et al.,Phys.Rev.Lett.87(2001)212502. [36]J.Schaffner and I.N.Mishustin,Phys.Rev.C 53(1996)1416. [37]J.Schaffner-Bielich,M.Hanauske,H.St?cker,and W.Greiner,Phys.Rev.Lett.89(2002)171101. [38]H.Shen,Phys.Rev.C 65(2002)035802. [39]W.L.Qian,R.K.Su,and H.Q.Song,J.Phys.G 30(2004)1893. [40]I.Bednarek and R.Manka,J.Phys.G 31(2005)1009. [41]A.Li,W.Zuo,A.J.Mi,et al.,Chin.Phys.16(2007)1934. [42]F.Yang and H.Shen,Phys.Rev.C 77(2008)025801. [43]A.J.Mi and W.You,Commun.Theor.Phys.53(2010)133. [44]Z.Yu,G.Z.Liu,M.F.Zhu,et al.,Nucl.Phys.A 834(2010)97c. [45]Z.Yu and W.B.Ding,Commun.Theor.Phys.55(2011)643. [46]M.Rufa,J.Schaffner,J.Maruhn,et al.,Phys.Rev.C 42(1990)2469. [47]B.D.Serot and J.D.Walecka,Advances in Nuclear Physics,16 eds.J.W.Negele and E.Vogt,Plenum,N.Y.(1986);B.D.Serot,Rep.Prog.Phys.55(1992)1855. [48]J.Schaffener,C.B.Dover,A.Gal,et al.,Phys.Rev.Lett.71(1993)1328. [49]J.Schaffner,C.B.Dover,A.Gal,et al.,Ann.Phys.235(1994)35. [50]M.Prakash,I.Bombaci,M.Prakash,et al.,Phys.Rept.280(1997)1. [51]H.Zhang and H.Y.Jia,Commun.Theor.Phys.45(2006)901. [52]Y.Sugahara and H.Toki,Nucl.Phys.A 579(1994)557. [53]I.Vidana,A.Ramos,and A.Polls,Phys.Rev.C 70(2004)024306. [54]J.Schaffner-Bielich and A.Gal,Phys.Rev.C 62(2000)034311. [55]J.K.Bunta and S.Gmuca,Phys.Rev.C 70(2004)054309. [56]F.?zel,Nature(London)441(2006)1115. [57]M.Alford,D.Blaschke,A.Drago,et al.,Nature(London)445(2007)7. [58]S.M.Ransom,J.W.T.Hessels,I.H.Stairs,et al.,Science 307(2005)892. [59]N.B.Zhang,B.Qi,S.Y.Wang,et al.,Int.J.Mod.Phys.E 22(2013)1350085. [60]D.L.Benjamin,N.Mohit,and J.O.Benjamin,Phys.Rev.C 73(2006)024021. [61]J.M.Lattimer and B.F.Schutz,Astrophys.J.629(2005)979. [62]W.Z.Jiang,B.A.Li,and F.J.Fattoyev,Eur.Phys.J.51(2015)119. [63]D.R.Zhang,W.Z.Jiang,S.N.Wei,et al.,Eur.Phys.J.52(2016)142.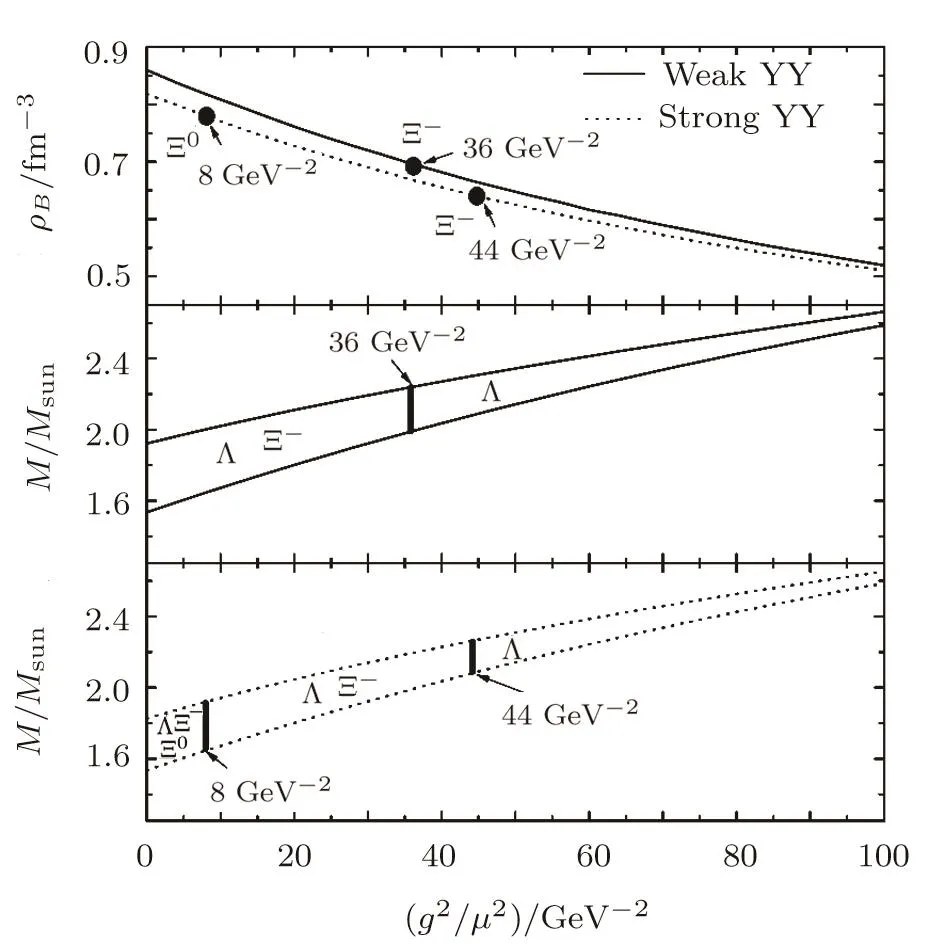
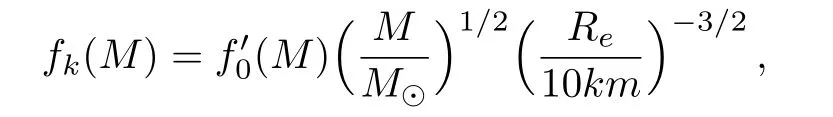
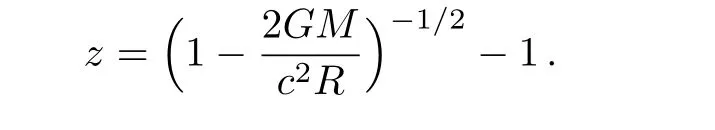

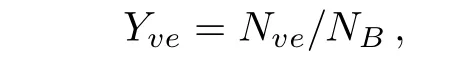
4 Conclusions and Discussions
 Communications in Theoretical Physics2018年4期
Communications in Theoretical Physics2018年4期
- Communications in Theoretical Physics的其它文章
- Effects of Low Anisotropy on Generalized Ghost Dark Energy in Galileon Gravity
- Influence of Non-linear Radiation Heat Flux on Rotating Maxwell Fluid over a Deformable Surface:A Numerical Study
- Numerical Study of Mixed Convective Peristaltic Flow through Vertical Tube with Heat Generation for Moderate Reynolds and Wave Numbers
- Melting Heat in Radiative Flow of Carbon Nanotubes with Homogeneous-Heterogeneous Reactions
- Controlling Thermal Conduction by Graded Materials?
- Direct Urca Processes Involving Proton1S0Superfluidity in Neutron Star Cooling?
