Alexander A.Okandeji,Muhammad R.A.Khandaker,WONG Kai Kit,ZHANG Yangyang,and ZHENG Zhongbin

(1.Department of Electrical and Computer Engineering,Ighinedion University Okada,PMB 0006,Benin city,Edo State,Nigeria;

2.Department of Electronic and Electrical Engineering,University College London,WC1E 7JE,United Kingdom;

3.Kuang Chi Institute of Advanced Technology,Shenzhen 518057,China;

4.East China Institute of Telecommunications,China Academy of Information and Communications Technology,Shanghai 200001,China)

1 Introduction

Since the continuous operation of wireless devices is mostly constrained by the limited capacity of their power sources,radio frequency(RF)energy harvesting(EH)has been identified as a promising technique to power future wireless devices.Technically,RF signals that carry information can also be used as a vehicle for transporting energy at the same time.For this reason,the study of simultaneous wireless information and power transfer(SWIPT)has attracted huge interest from industrial and academic communities[1][7].Effectively,wireless data and energy access can be made available to mobile users through the application of SWIPT,which in turn gives mobile users great convenience.SWIPT technology has been practically deployed in wireless communication networks.For example,[8]considered the practical deployment of SWIPT in a wireless sensor network mounted at a remote and difficult to access location,and powered only by a battery with limited operation time.Recharging or replacing the battery may be inconvenient,and often attract huge cost.Consequently,electromagnetic energy emanating from numerous radio and television broadcasting in the environment may serve as an opportunistic as well as greener alternative for harvesting energy to power such devices.

SWIPT was first introduced in[9]to describe the trade off between the rates at which energy and dependable information is transmitted over a noisy channel and thus,a capacity energy function was proposed.A key assumption in[9]was the possibility of the receiver capable of simultaneously decoding information and harvesting energy from the same received signal.However,this assumption does not hold in practice as practical circuits for harvesting energy from the received signal are notable to decode information directly.Consequently,to facilitate wireless information and power transfer at the receiver,the work done in[10]proposed two practical receiver architecture designs for SWIPT,namely time switching(TS)and power splitting(PS).Specifically,in the TS design architecture,the receiver switches over time to achieve information decoding and energy harvesting,while with PS,the receiver splits the receive signal into two streams of different power in order to decode information and harvest energy separately.It was shown in[10]that PS generally achieves better performance than TS as the TS receiver architecture scheme,in general,can be regarded as a special form of PS with only a binary split power ratio.In this paper,we focus on the PS design architecture.

Conventionally,half-duplex(HD)communication modes,in which the transmission and reception of radio signals occur over orthogonal time or frequency resources in order to avoid crosstalk,have been employed for wireless communications.Recent advances,however,suggest full-duplex(FD)communications that allow simultaneous transmission and reception of signals over the same radio channel in order to maximally use the limited available spectral resource[11],[12].The key challenge to achieve FD communications is the presence of self-interference(SI).Thus,for wireless communication systems to communicate in FD mode,the generated SI must be significantly suppressed,if not can celled completely,to receiver’s noise floor[13].Digital SI cancellation(SIC)for FD wireless systems was studied in[14].Authors in[14]demonstrated the possibility of achieving SIC of 70 dB and 76 dB for antenna separation and digital cancellation at 20 cm and 40 cm spacing,respectively,between interfering antennas.It suffices to say therefore that radios can work in FD if SI can be significantly suppressed.Interestingly,the study of FD systems brings a new opportunity for SWIPT in FD systems[1],[7].In particular,authors in[1]investigated the end-to-end sum-rate maximization approach for SWIPT in FD system while maintaining the energy harvesting threshold at each node by optimizing the receive power splitter and transmit power at each node.In contrast,[7]investigated the joint optimization of the transmit power at the source nodes and the two way relay beamforming matrix for SWIPT with a FD MIMO amplify and forward(AF)relay employing PS,where the achievable sum-rate is maximized subject to energy harvesting and individual power constraints.

Wireless communication networks are susceptible to eavesdropping;however,SWIPT systems are more susceptible to eavesdropping due to the inherent characteristics of SWIPT and the open nature of wireless channel.The security issue in SWIPT systems is therefore a critical issue that needs to be addressed.Existing works on communication security have adopted the cryptographic technique.Although this technique may guarantee communication security to some degree in the application layer,the suitability of these technique on SWIPT systems is not guaranteed since it requires complex encryption/decryption algorithms and key distribution[15].Alternatively, physical-layer(PHY)security has been identified to perfectly guarantee secure wireless information transmission against eavesdropping by using the physical properties of wireless channels such as fading and interference[16],[17].In this context,artificial noise(AN),injected into the transmitted signal,is used to confuse the eavesdropper[18].

The fundamental study of the integration of PHY security and SWIPT was first considered in[15].In particular,authors in[15]investigated the joint design of the beamforming vectors and power allocation to maximize the secrecy rate or the total harvested energy under a multi-user multiple-input single-output(MISO)SWIPT scenario.The work done in[19]proposed a robust secure transmission scheme which mini mises the total transmit power in a multi-user MISO SWIPT system.In contrast,authors in[20]and[21]extended the study of PHY security into a multiple-input multiple output(MIMO)broadcast SWIPT system.To maximise the secrecy rate in a MIMO SWIPT scenario,[20]investigated the secure transceiver beamforming design while ensuring efficient energy harvesting.On the other hand,authors in[21]considered the harvested energy maximization approach subject to secure information transmission by designing the transmit covariance.

In contrast to existing works,this paper considers the novel integration of SWIPT,FD technology and PHY security.In particular,this paper extends the secure HD MISO SWIPT communication scenario in[22]to the FD case,where the harvested energy at the MSs is utilized to send feedback information to the BS.We aim to minimize the end-to-end transmit power for SWIPT in FDMISO systems(Fig.1)while satisfying the secrecy rate at each MSs,and the QoS requirements for each MS by optimizing jointly the receive PS ratio and the transmit power at the MSs,the beamforming matrix at the BS,and the AN covariance matrix.Specifically,we assume perfect CSI,which is accomplished from fine estimation by transmitting dedicated training symbols at the receiver,for the uplink and downlink channels for the MISO SWIPT system.In contrast,loop channels are assumed to be imperfect due to the fact that the distribution of SI channels are unknown.Also,SI channel measurement results obtained in[23]indicate that the SI channel has a multi path nature.Specifically,it was shown in[23]that multiple paths arising from SI channel measurements are known to have higher power relative to the line-of-sight(LOS)path.Consequently,there is the need to suppress SI with multiple path nature,through the use of an adaptive cancellation technique whose measurement can be used to cancel both the LOS path and the delayed version of the same,which is not the objective to be achieved in this work.Nonetheless,for convenience,SI channels can be modelled as Gaussian channels[7].Accordingly,due to insufficient knowledge of the SI channel,a deterministic model for channel uncertainties is considered,where the magnitude of the estimation error as well as the SI power is bounded.Since the problem is non-convex,we propose an alternating optimization approach.

We denote scalars by non bold letters and boldface lowercase letters are used to represent vectors,while boldface uppercase letters are used for matrices.For a square matrix A,Tr(A),Rank(A),ATand AHdenote its trace,rank,transpose and conjugate transpose,respectively,whilemeans that A is a positive semidefinite matrix.Also,Indenotes an n×n identity matrix,‖?‖returns the Euclidean norm.The distribution of a circularly symmetric complex Gaussian(CSCG)random vector with mean μ and covariance matrix C is denoted by(μ,C).Finally,?m×ndenotes the space of m×n complex matrices.

2 System Model and Problem Statement

2.1 System Model

In this paper,we consider the end-to-end transmit power minimization approach for secure SWIPT in a MISO FD system where the BS simultaneously transmits K independent confidential messages to K dual-antenna(one for transmission,one for reception)receivers in the downlink,in the presence of L external single-antenna eavesdroppers,and receives information in the uplink in FD mode.In addition to the external eavesdroppers,each receiver attempts to eavesdrop messages intended for other receivers.Hence we call them potential eavesdroppers.To ensure secure information transmission,AN is superimposed to the transmitted signal to confuse these potential as well as the external eavesdroppers.We denote the number of transmit and receive antennas at the BS,respectively,as Ntand Nr,and each MS uses an identical pair of transmitter and receiver antennas for signal transmission and reception.In the downlink transmission,the BS performs transmit beamforming to send information to the receivers while the MSs,using the harvested energy from the received signal,send feedback to the BS in the uplink with transmit power Pup,k,k=1,...,K.Therefore,the complex baseband signal transmitted at the BS is expressed as

where sk～(0,1)denotes the confidential message intended for the k th receiver,ak∈ ?Nt×1denotes the corresponding precoding vector.b ∈ ?Nt×1is the AN vector modelled as b ～(0,V),where V=bbHdenotes the covariance matrix of b.For convenience,we use={1,...,K},?={1,...,L}and?k={1,...,k1,k+1,...,K}to denote the index set of receivers,external eavesdroppers,and receivers except the k th receiver,respectively.The received signal at the k th receiver and l th external eavesdropper can be expressed as

Then,the energy harvesting rate(i.e.,power)at the k th EH can be expressed as[22]

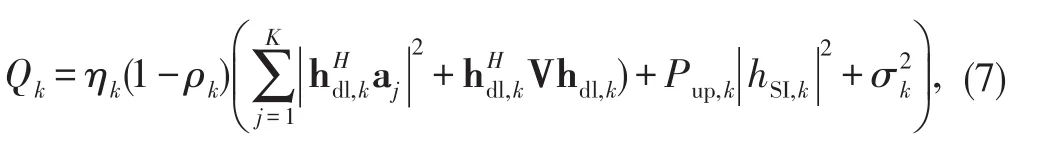
where ηkis the energy conversion efficiency which for notational simplicity is assumed to be unity throughout this paper.

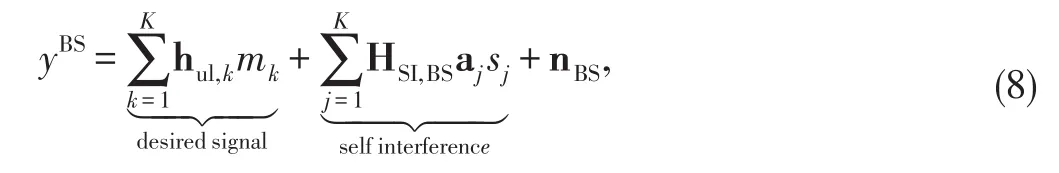
where hulis the channel vector from the MS to the transmit antennas at the BSand nBSdenotes the additive white Gaussian noise(AWGN)vector at the BS modelled asTo equalize the uplink signal from MS,we assumekthat the BS applies a receive beamformer wkexpressed as given in[24]

Therefore,the SINR at the BS for the k th user’s signal can be written as[24]

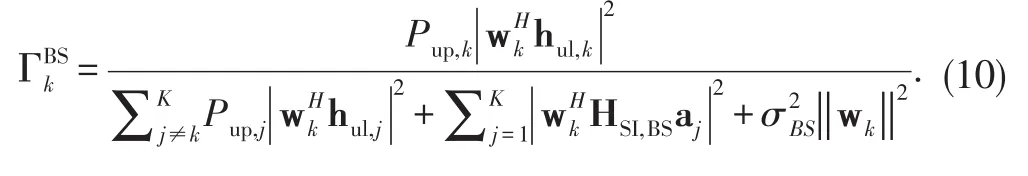
As in[22],we also assume that the legitimate receivers themselves may attempt to overhear the signals transmitted to other receivers and we want to guarantee secrecy against any such attempt.As such,we denote the received SINR which corresponds to the signal transmitted for the k th receiver at the m th potential eavesdropper and the l th external eavesdropper as

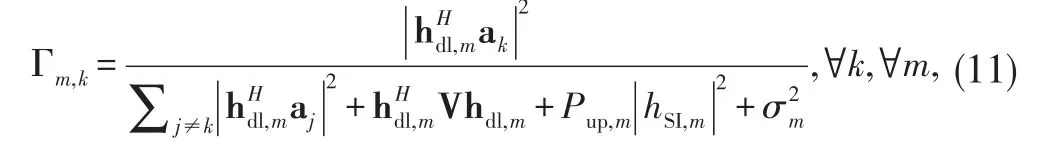
and

In this work,the communication security is considered from the viewpoint of individual security[25],[26].Consequently,the achievable individual secrecy rate at the k th receiver is given as[22]

where[x]+=max(0,x).

2.2 Modelling the SI

Due to the insufficient knowledge of the SI channel,it is impossible to completely eliminate residual SI(RSI).For this reason,we consider a deterministic model for imperfect SI channels.In particular,the actual SI channels hSI,kand HSI,BSare assumed to respectively lie in the neighbourhood of the estimated channels h?SI,kand H?SI,BSthat are available at the corresponding nodes.Therefore,the actual channels due to imperfect channel estimates can be modelled as

where△hSI,kand△HSI,BSrepresent the channel uncertainties assumed to be bounded as

for some ?1,?2≥0.It is worth noting that the bounding values{?k} are dependent on the accuracy of the CSI estimates.Consequently,to efficiently define the worst case SI level,we modify(14a)and(14b)using the triangle inequality and the Cauchy Schwarz inequality,respectively[27].It follows from(14a)and(14b)that

Note that in the absence of statistical information about the error,we use?kto represent the minimal knowledge of the upper bound of the channel error which is sufficient enough to describe the error.Thus from(16a)and(16b),we obtain

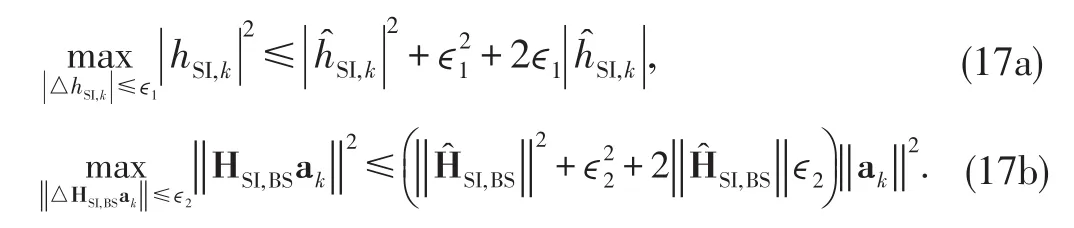
In addition,it holds that

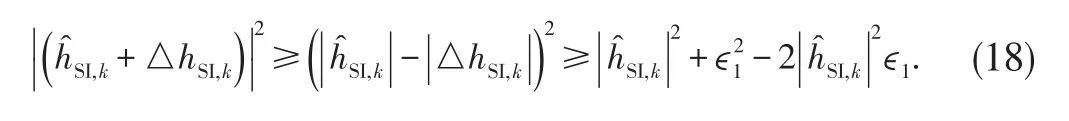
Here,we assume,in general,thatimplies that the erroris sufficiently small relative to the estimate or the estimate is not meaningful.Consequently,

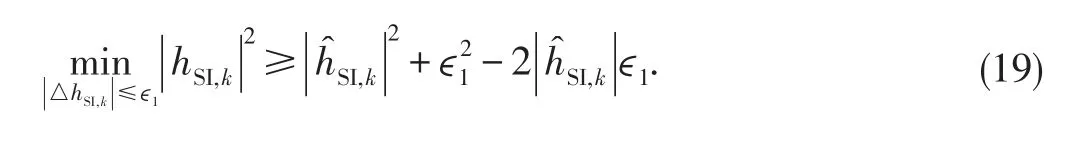
2.3 Problem Statement

In this work,we consider the case where each MSkis characterised by strict quality of service(QoS)requirement.In particular,to ensure a continuous information transfer,the QoS constraints require that the SINR of the downlink channel at all times should be above a given threshold denoted by.Furthermore,it is required that the harvested energy by each MSmustbe above a certain useful level specified by a prescribed threshold denoted by Qk,?k.In addition,for the uplink channel,we also assume that each MS is expected to send feedback to the BS and a strict QoS is required such that the SINR of the uplink channel is expected to be higher than a given threshold denoted as

FD communication is feasible subject to the effective cancellation of SI.As an increase in transmit power causes a corresponding increase in the SI,it is important for communication nodes to transmit at optimality.To this end,our aim is to minimize the total transmit power while maintaining the achievable secrecy rate and energy harvesting constraints at each receiver as well as the nonzero uplink and downlink SINR( γUL＞0;γDL＞0).We achieve this by jointly designing the transmit beamforming vector(a)at the BS,the AN covariance(V),the uplink transmit power(Pup,k)and the receive PS ratio( ρk)at MSk,k=1,...,K.Thus we formulate the optimization problem as

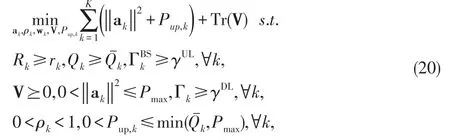
where Rkand Qˉk,respectively,denote the required secrecy rate and the energy harvesting constraints at each receiver.Problem(20)can explicitly be written as given in(21).Problem(21)is a non-convex problem due to the coupled optimization variables in the constraints,and hence it is very difficult to solve in closed form.Thus,we solve(21)in an alternating manner.

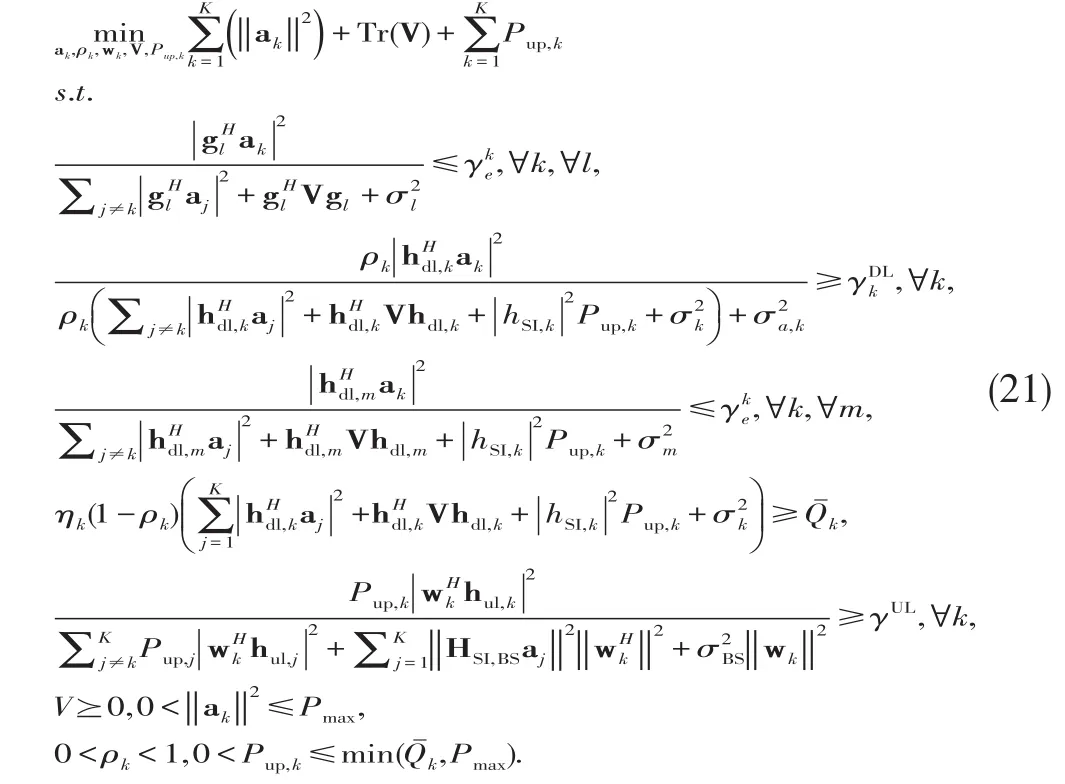
It is worth noting that the upper bound of the SI at the BS and the MSkis obtained when the source node transmits at maximum available power[24],i.e.,.Consequently,we denote the upper bounds of the SI power at the BS and MSkas Eˉand Gˉ,respectively.Thus,the optimization problem in(21)can be upper bounded as given in(22).

To solve problem(22),first we observe that the QoS uplink constraint does not have the PS coefficient and this is because the BS does not need to harvest energy.As a consequence,problem(22)can be decomposed into two subproblems given in(23)and(24),

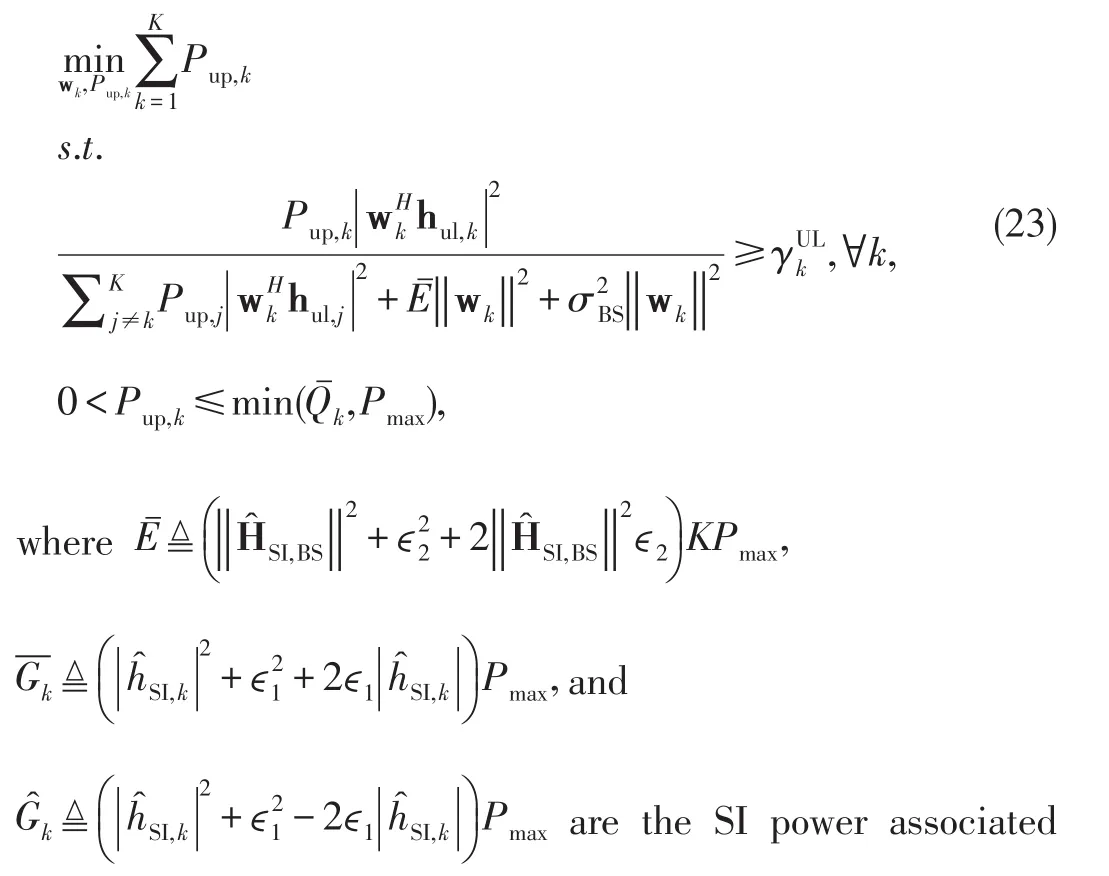
with the energy harvesting constraints.

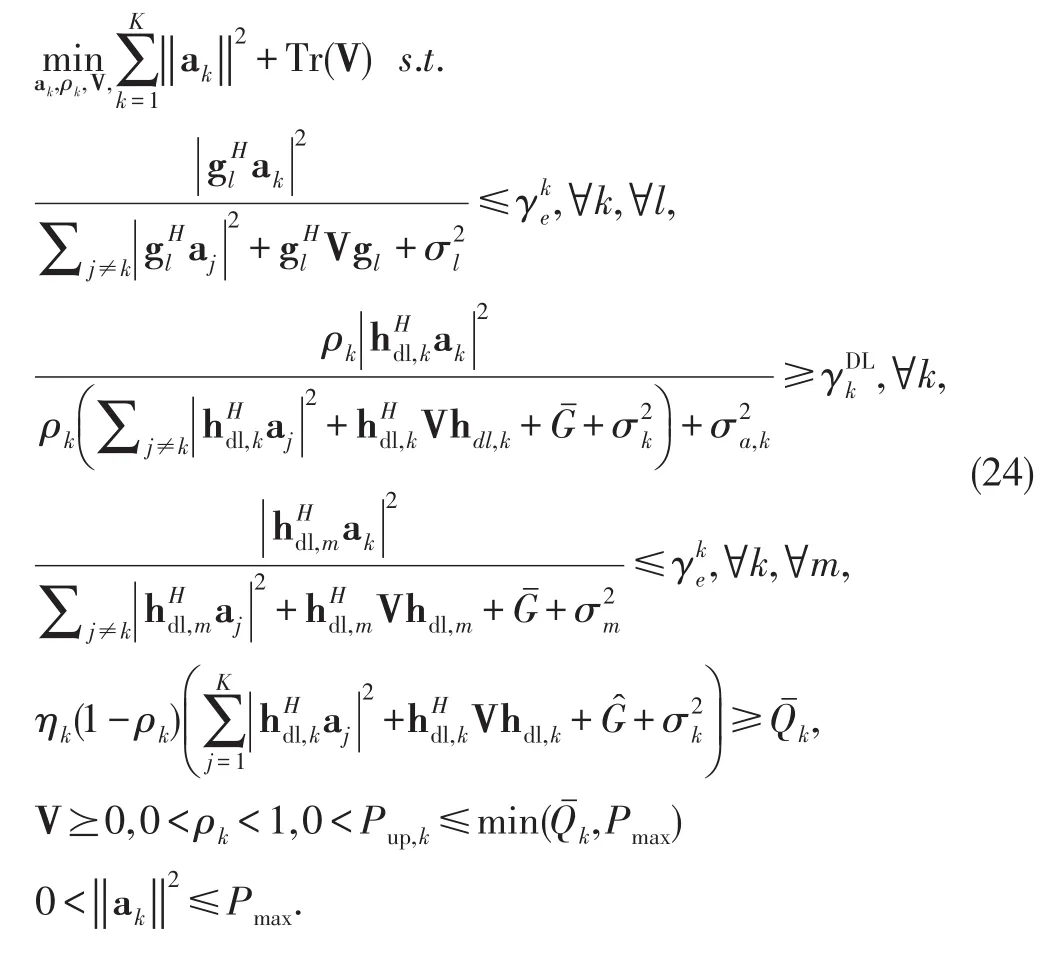
Note that problem(23)corresponds to optimizing the variables involved in the uplink while problem(24)corresponds to those in the downlink.We then apply semidefinite relaxation(SDR)to the subproblems as discussed below.

3 Proposed Solution

Clearly,even with the fixed set of,problem(22)is non-convex.As a result of the possibility of decomposing problem(22)into two subproblems,namely,problems(23)and(24),we will solve problem(23)analytically and use SDR technique to solve(24).

We first proceed by solving problem(23)to determine the optimal value ofandThe optimal receivercan be defined as the Wiener filter[28]

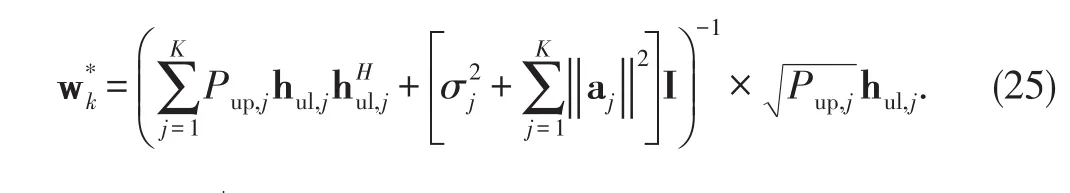
s.t.

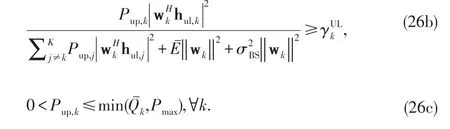
Upon investigation,the optimalis the minimum Pup,kwhich satisfies(26b)to equality.Consequently,optimalis given by

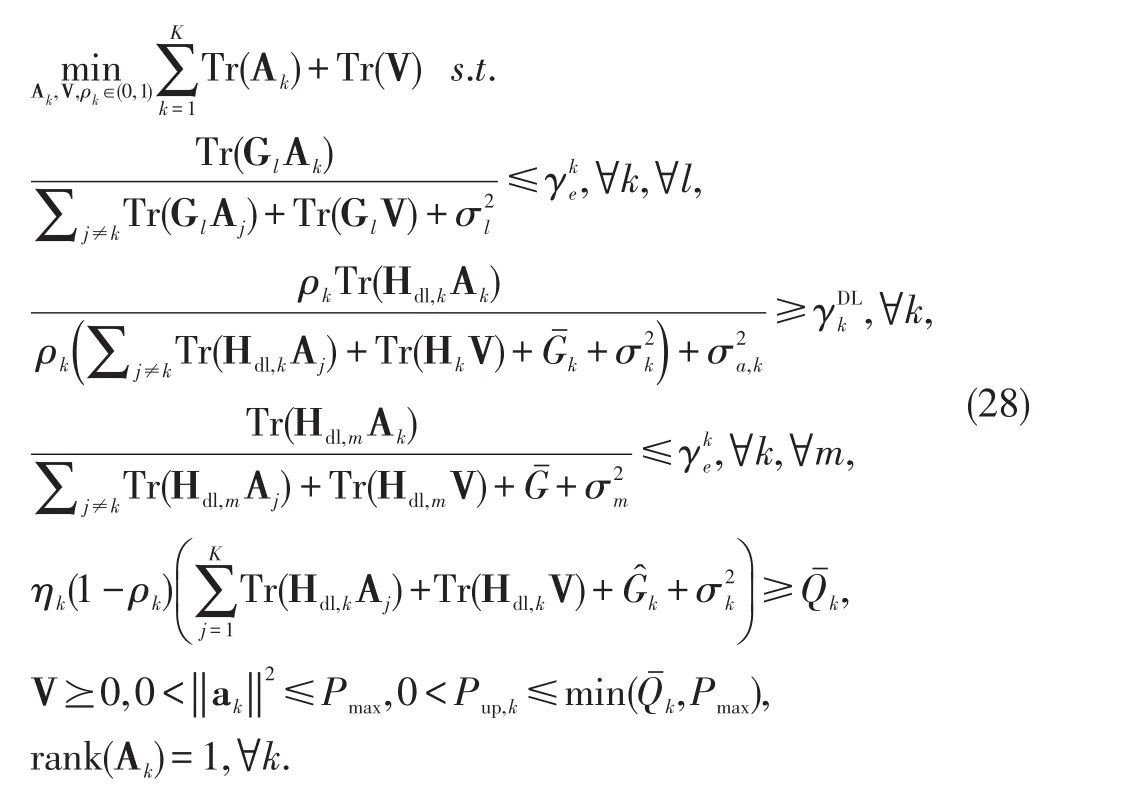
Note that problem(28)is still non-convex due to the non-convex rank-one constraints and the coupled optimization variables Akandρk.Applying SDR technique,after dropping the rank-one constraint,problem(28)can be reformulated into the following problem:

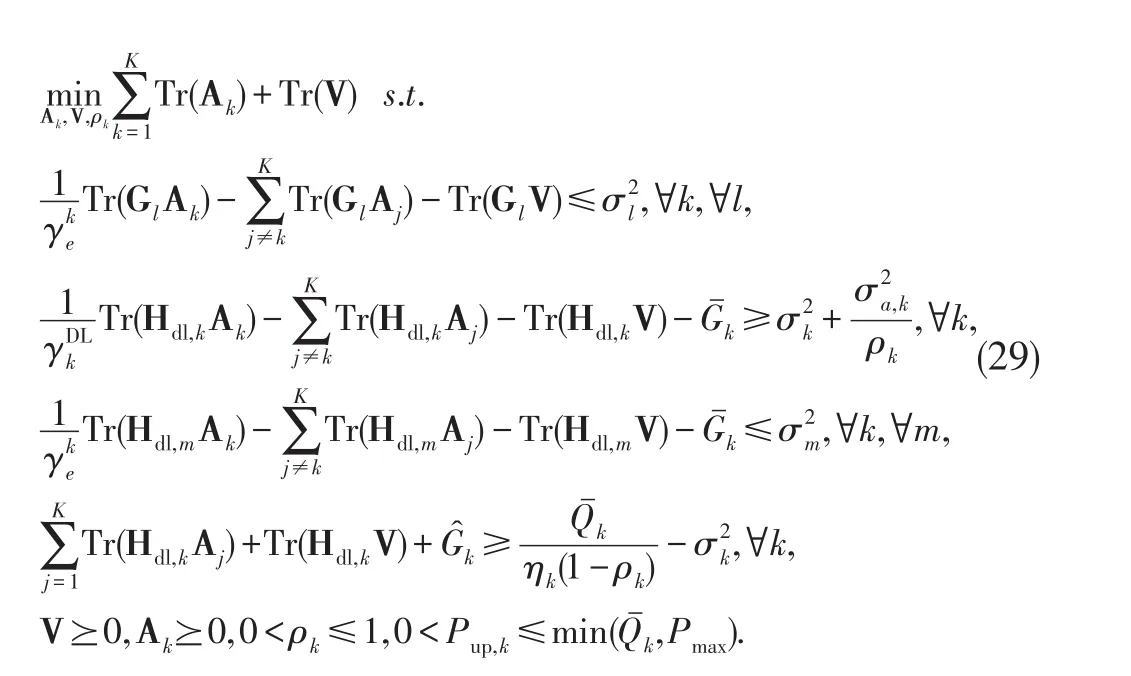
Proposition 1:There always exists an optimal solutionfor problem(29)such that rank

To summarise,Proposition 1 implies that the relaxation is tight,and thus the globally optimal solution of problem(24)can be obtained.SWIPT in MISO FD system versus the harvested power threshold for given values of the uplink and downlink SINR.As can be observed,as the harvested power threshold increases,the secrecy sum rate increases.Technically,an increase in the harvested power allows more power to be directed to the ER of each MS,thus less power for SI,which invariably increases the secrecy sum-rate.

In Fig.4,the achievable secrecy sum-rate for secure

4 Numerical Exam p les

In this section,numerical examples are provided.In particular,the performance of the proposed joint beamforming design(Joint Opt in Fig.2)for secure SWIPT in MISO FD systems is evaluated through simulations.We simulate a flat Rayleigh fading environment in which the channel fading coefficients are characterized as complex Gaussian numbers with zero mean and are independent and identically distributed,and we assume there are K=2 MSs and all MSs have the same set of parameters,i.e.,and yE=15 dB.We also assume that 70%of the SI power has been cancelled using existing SI cancellation techniques[14].All simulations are averaged over 1000 independent channel realizations.

In Fig.2,we investigate the achievable secrecy sum-rate for secure SWIPT in MISO FD system versus the uplink SINR target for all MSs for fixed values of the downlink SINR(γDL=5 dB),the harvested power threshold,and the eavesdropper’s SINR(yE=15 dB).Fig.2 shows the performance comparison between the joint optimization and the fixedρoptimization.As can be observed,an increase in the uplink SINR corresponds to a decrease in the secrecy sum-rate due to increase in transmission power which invariably increases the generated SI.However,the joint optimization scheme outperforms the fixed ρ optimization.Also,as the harvested power threshold increases,the secrecy sum-rate decreases,but the joint optimization scheme outperforms the fixed ρoptimization scheme.

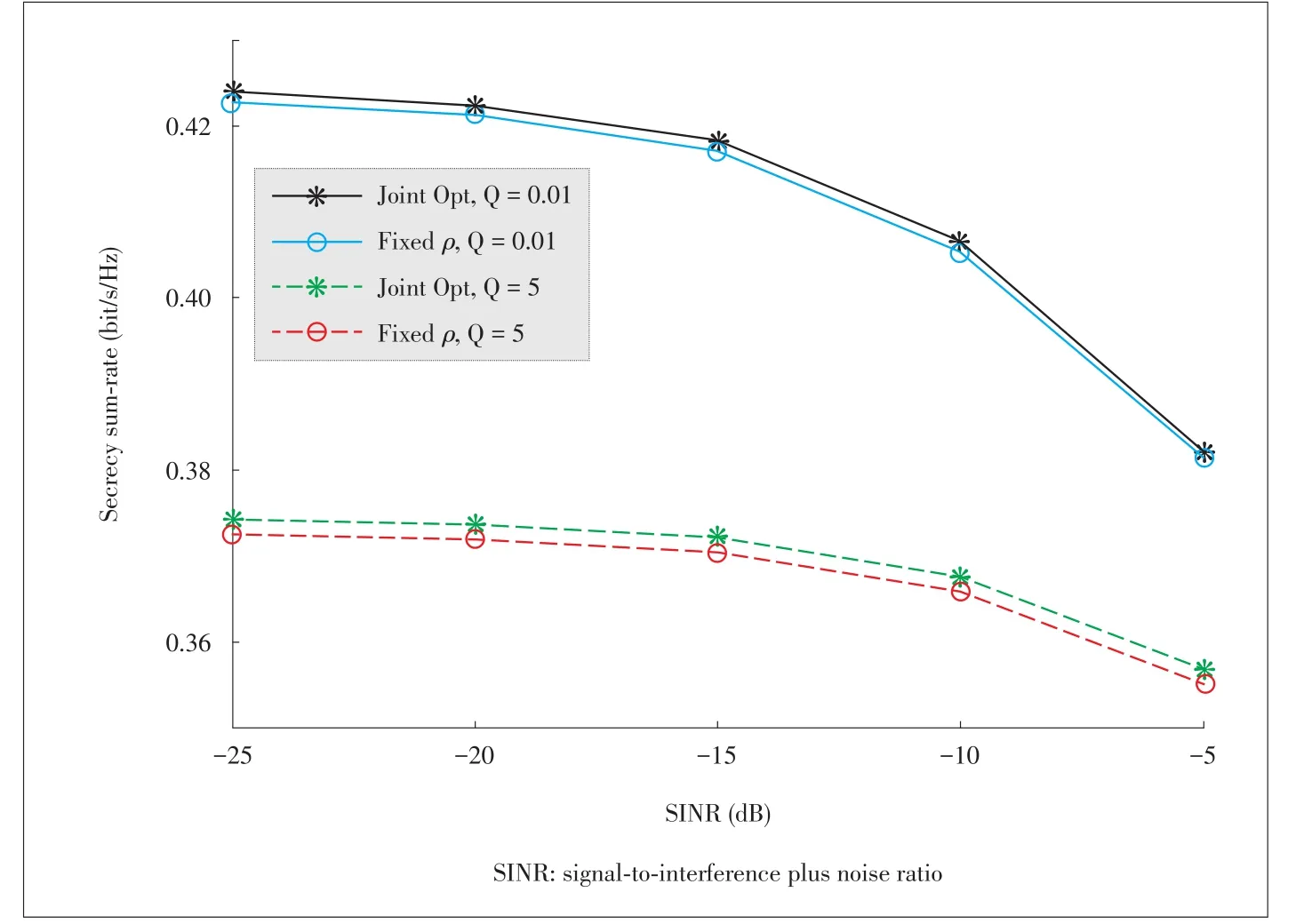
▲Figure2.Secrecy sum-rate versus SINR γUL.

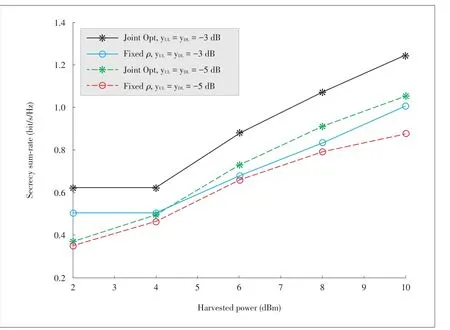
▲Figure3.Secrecy sum-rate versus harvested power.

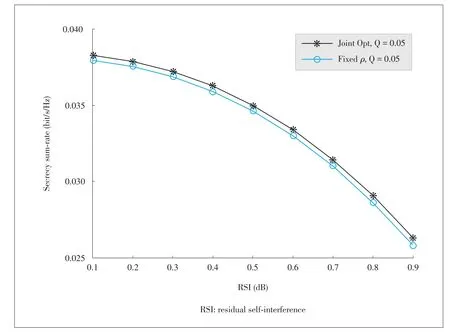
▲Figure4.Secrecy sum-rateversus RSI.

In Fig.3,we further investigate the achievable secrecy sum-rate for secure SWIPT in MISO FD system versus the residual SI is investigated.In particular,we investigate the performance comparison of the proposed system for both joint optimization,and optimization with a fixedρ.Clearly,an increase in the RSI results in a corresponding decrease in the achievable secrecy rate.However,the joint optimization scheme outperforms the optimization scheme with fixed ρ.Thus,a need for joint optimization is justified.

5 Conclusions

In this paper,we investigated the secure beamforming design for SWIPT in MISO FD system.To reduce SI and achieve secure FD transmission,the end-to-end sum transmit power has been minimized subject to the given SINR and harvested power constraints for each MS.In particular,to achieve optimal system performance,using SDR technique,we jointly optimized the transmit beamforming vector at the BS,and the received PS ratio and the transmit power at the MSs,and the AN covariance matrix.We show the need for joint optimization of system parameters through the numerical results.

[1]A.A.Okandeji,M.R.A.Khandaker,and K K.Wong,“Wireless information and power transfer in full-duplex communication systems,”in Proc.IEEE International Conference on Communications,Kuala Lumpur,Malaysia,2016.doi:10.1109/ICC.2016.7511169.

[2]A.A.Okandeji,M.R.A.Khandaker,and KK.Wong,“Two way relay beamforming optimization for full-duplex SWIPT systems,”in Proc.24th European Signal Processing Conference,Budapest,Hungary,2016.doi:10.1109/EUSIPCO.2016.7760674.

[3]J.Liao,M.R.A.Khandaker,and K.K.Wong,“Robust power splitting SWIPT beam forming for broadcast channels,”IEEE Communications Letters,vol.20,no.1,pp.181184,2016.doi:10.1109/LCOMM.2015.2498928.

[4]M.R.A.Khandaker and K.K.Wong,“SWIPT in MISOmulticasting systems,”IEEE Wireless Communications Letters,vol.3,no.3,pp.277280,2014.doi:10.1109/WCL.2014.030514.140057.

[5]M.R.A.Khandaker and K.K.Wong,“QoS based multicast beamforming for SWIPT,”in Proc.IEEE SECON Workshop Energy Harvesting Communications,Singapore,Singapore,2014,pp.6267.doi:10.1109/SECONW.2014.6979707.

[6]Q.Shi,L.Liu,W.Xu,and R.Zhang,“Joint transmit beam forming and receive power splitting for MISO SWIPT systems”IEEE Transactions on wireless Communications,vol.13,no.6,pp.32693280,Jun.2014.doi:10.1109/TWC.2014.041714.131688.

[7]A.A.Okandeji,M.R.A.Khandaker,KK.Wong,and Z.Zheng,“Joint transmit power and relay two way beam forming optimization for energy harvesting full-duplex communications,”in Proc.IEEE Globecom International Workshop on Full Duplex Wireless Communications,Washington DC,USA,2016.doi:10.1109/GLOCOMW.2016.7848948.

[8]R.Zhang and C.K.Ho,“MIMO broadcasting for simultaneous wireless information and power transfer,”IEEE Transactions on wireless Communications,vol.12,no.5,pp.19892001,May 2013.doi:10.1109/TWC.2013.031813.120224.

[9]L.Varshney,“Transporting information and energy simultaneously,”in Proc.IEEE International Symposium on Information Theory,2008,pp.16121616.doi:10.1109/ISIT.2008.4595260.

[10]X.Zhou,R.Zhang,and C.K.Ho,“Wireless information and power transfer:architecture design and rate energy trade off,”IEEE Transactions on Communications,vol.61,no.11,pp.47544767,Nov.2013.doi:10.1109/TCOMM.2013.13.120855.

[11]M.Duarte,C.Dick,and A.Sabharwal,“ Experiment driven characterization of full-duplex wireless systems,”IEEE Transactions on Wireless Communications,vol.11,no.12,pp.42964307,Dec.2012.doi:10.1109/TWC.2012.102612.111278.

[12]Y.Hua,P.Liang,Y.Ma,A.C.Cirik,and Q.Gao,“A method for broad band full-duplex MIMO radio,”IEEE Signal Processing Letters,vol.19,no.12,pp.793796,Dec.2012.doi:10.1109/LSP.2012.2221710.

[13]E.Ahmed and A.M.Eltawil,“Alldigital self-interference cancellation technique for full-duplex systems,”IEEE Transactions on Wireless Communications,vol.14,no.7,pp.35193532,Jul.2015.doi:10.1109/TWC.2015.2407876.

[14]M.Duarte and A.Sabharwal,“Fullduplex wireless communication using off the shelf radios:feasibility and first result,”in IEEE ASILOMAR,Pacific Grove,USA,2010.doi:10.1109/ACSSC.2010.5757799.

[15]L.Liu,R.Zhang,and K.C.Chua,“Secrecy wireless information and power transfer with MISO beamforming,”IEEE Transactions on Signal Processing,vol.62,no.7,pp.18501863,Apr.2014.doi:10.1109/TSP.2014.2303422.

[16]W.C.Liao,T.H.Chang,W.K.Ma,and C.Y.Chi,“ QoS based transmit beam forming in the presence of eavesdroppers:an optimized artificial noiseaided approach,”IEEE Transactions on Signal Processing,vol.59,no.3,pp.13171322,Mar.2011.doi:10.1109/TSP.2010.2094610.

[17]J.Zhu,R.Schober,and V.K.Bhargava,“Secure transmission in multicell massive MIMO systems,”IEEE Transactions on Wireless Communications,vol.13,no.9,pp.47664781,Jul.2014.doi:10.1109/TWC.2014.2337308.

[18]Q.Liand D.Han,“Sum secrecy rate maximization for full-duplex two way relay networks,”in Proc.IEEE International Conference on Acoustics,Speech and Signal Processing,Shanghai,China,pp.36413645,Mar.2016.doi:10.1109/ICASSP.2016.7472356.

[19]D.W.K.Ng,E.S.Lo,and R.Schober,“Robust beam forming for secure communication in systems with wireless information and power transfer,”IEEE Transactions on Wireless Communications,vol.13,no.8,pp.45994615,Aug.2014.doi:10.1109/TWC.2014.2314654.

[20]Q.Shi,W.Xu,J.Song,and E.Song,“Secure beamforming for MIMO broadcasting with wireless information and power transfer,”IEEE Transactions on Wireless Communications,vol.14,no.5,pp.28412853,May 2015.doi:10.1109/TWC.2015.2395414.

[21]W.Wu and B.Wang,“Efficient transmission solutions for MIMO wiretap channels with SWIPT,”IEEE Communications Letters,vol.19,no.9,pp.15481551,Jun.2015.doi:10.1109/LCOMM.2015.2451179.

[22]H.Zhang,Y.Huang,C.Li,and L.Yang,“Secure beamforming design for SWIPT in MISO broadcast channel with confidential messages and external eavesdroppers,”IEEE Transactions on Wireless Communications,vol.15,no.11,pp.78077819,Nov.2016.doi:10.1109/TWC.2016.2607705.

[23]A.Sethi,V.Tapio,and M.Junti,“Self interference channel for full duplex Transceiver”in Proc.IEEE Wireless Communications and Networking Conference,Istanbul,Turkey,2014.doi:10.1109/WCNC.2014.6952167.

[24]A.A.Okandeji,M.R.A.Khandaker,KK.Wong,et al.,“SWIPT in MISO full-duplex systems,”Journal of Communications and Networks,to be published.

[25]J.Lie,Z.Han,M.A.V.Castro,and A.Hjorungnes,“Secure satellite communication systems design with individual secrecy rate constraints,”IEEE Transactions on Information Forensics and Security,vol.6,no.3,pp.661671,Sept.2011.doi:10.1109/TIFS.2011.2148716.

[26]A.S.Mansour,R.F.Schaefer,and H.Boche,“The individual secrecy capacity of degraded multi-receiver wiretap broadcast channels,”in Proc.IEEE International Conference on Communications,London,UK,2015,pp.41814186.doi:10.1109/ICC.2015.7248979.

[27]S.Boyd and L.Vandenberghe,Convex Optimization.Cambridge,UK:Cambridge University Press,2004.

[28]D.H.N.Nguyen,L.B.Lem,and Z.Han,“Optimal uplink and downlink channel assignment in a full-duplex multi-user system,”in Proc.IEEE International Conference on Communications,Kuala Lumpur,Malaysia,May 2016.doi:10.1109/ICC.2016.7510742.

[29]M.Grant and S.Boyd.(2010,Apr.).CVX:Matlab software for disciplined convex programming[Online].Available:http://cvxr.com/cvx