湖北省陽新縣高級中學(xué)(435200) 鄒生書

題目1 已知x,y,z∈R+,且x+y+z=1,求S=x2+2y2+z3的最小值.

分析本題是一道約束條件下的三元函數(shù)的最小值問題.約束條件和所求式子都是多項式,變量之間除了整體的關(guān)系相對獨立沒有交集,并且所求式子中變量的指數(shù)都比條件中相同變量的指數(shù)高.象這樣約束條件是低次的多元等式或不等式,所求的是高次的多變元函數(shù)的最小值問題,我們可以通過引入待定常數(shù)將所求與已知融合,然后獨立構(gòu)造以各個變元為自變量的函數(shù),最后以各個獨立函數(shù)的最小值換取整體的最小值.

解因為x+y+z=1,引入待定常數(shù)λ∈[0,1],則

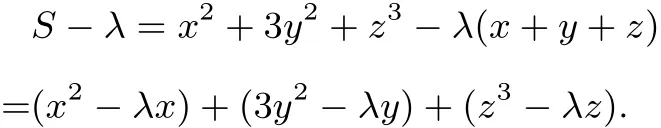
設(shè) f(x)=x2? λx,x ＞ 0,則 f′(x)=2x? λ,易知當(dāng)時,f(x)取最小值.

設(shè) g(y)=3y2? λy,y ＞ 0,則 g′(y)=6y ? λ,易知當(dāng)時,g(y)取最小值.設(shè) h(z)=z3? λz,z ＞ 0,則 h′(z)=3z2? λ,易知當(dāng)時,h(z)取最小值.

題目2已知x,y,z∈R+,且,求的最小值.

解因為,引入待定常數(shù)λ∈[0,1],則

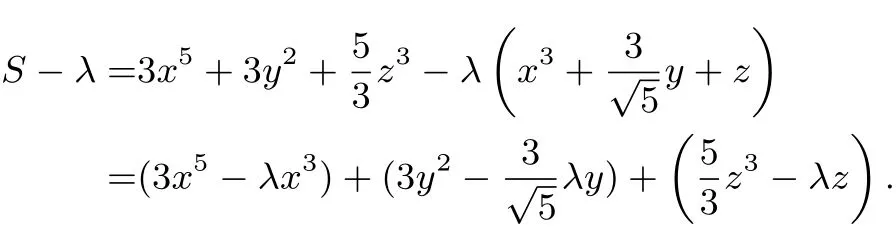
設(shè) f(x)=3x5?λx3(x ＞ 0),則 f′(x)=3x2(5x2?λ),易知當(dāng)時,f(x)取最小值.

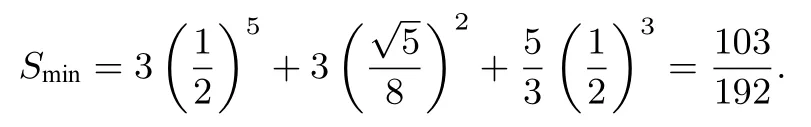
題目3已知非負(fù)實數(shù)x,y,z滿足x+y+z=1,求的最大值和最小值.

解由題設(shè)知x,y,z∈[0,1],所以x3≤x,等號當(dāng)且僅當(dāng)x=0或x=1時成立;y2≤y,等號當(dāng)且僅當(dāng)y=0或y=1時成立.所以,等號當(dāng)且僅當(dāng)x=y=0,z=1時成立.故的最大值為

因為x+y+z=1,引入待定常數(shù)λ∈[0,1],則

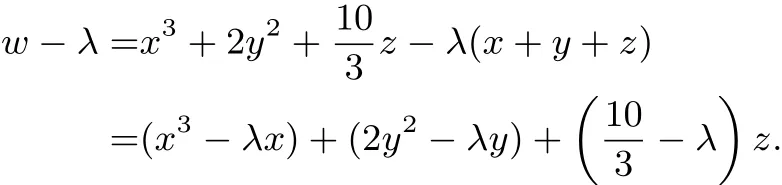
設(shè)f(x)=x3?λx,則f′(x)=3x2?λ,易知當(dāng)時,f(x)取最小值.

設(shè) g(y)=2y2? λy,則 g′(x)=4y? λ,易知當(dāng)時,g(y)取最小(值.)

題目4(《中等數(shù)學(xué)》2016年第7期數(shù)學(xué)奧林匹克高中訓(xùn)練題的第205題)已知5x+16y+33z≥136(x,y,z∈R+),則x3+y3+z3+x2+y2+z2的最小值為___.

解設(shè)f(x)=x3+x2?5x,x ＞ 0,則f′(x)=3x2+2x?5=(x?1)(3x+5),當(dāng)0＜x＜1時,f′(x)＜0;當(dāng) x ＞ 1時,f′(x)＞ 0,所以 f(x)min=f(1)= ?3,即x3+x2?5x≥?3,

設(shè) g(y)=y3+y2? 16y,y ＞ 0,則 g′(y)=3y2+2y?16=(y?2)(3y+8),當(dāng)0＜ y＜ 2時,g′(y)＜ 0;當(dāng) y＞ 2時,g′(y)＞ 0.所以 g(y)min=g(2)= ?20,即y3+2y2?16y≥?20,

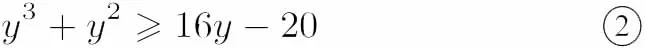
設(shè) h(z)=z3+z2? 33z,z ＞ 0,則 h′(z)=3z2+2z?33=(z?3)(3z+11),當(dāng)0＜ z＜ 3時,h′(z)＜ 0;當(dāng) z＞ 3時,h′(z)＞ 0.所以 h(z)min=h(3)= ?63,即z3+z2?33z≥?63,

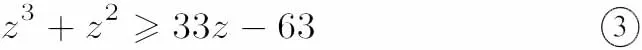
將不等式①—③相加得x3+y3+z3+x2+y2+z2≥5x+16y+33z?86,當(dāng)且僅當(dāng)x=1,y=2,z=3時等號成立.又當(dāng)x=1,y=2,z=3時,不等式5x+16y+33z≥136,等號成立,所以當(dāng)x=1,y=2,z=3時,x3+y3+z3+x2+y2+z2≥136?86=50,故所求最小值為50.

評注與前面三題相比本題條件是不等式并且構(gòu)造的函數(shù)有三項相比多了一項,若用待定系法求解反而非常困難,從上面解法不難看出,若用待定系數(shù)法,本題的待定的系數(shù)恰好是1,非常特殊,正是無巧不成書.題目巧雕作,解法本天成,妙手偶得之.

[1]劉康寧.從一道聯(lián)賽題談固定變量法求最值[J].中學(xué)數(shù)學(xué)教學(xué)參考(上),2017(11).

[2]萬家練,阮征.堅持獨立思考[J].數(shù)學(xué)通訊,2017(2上半月).