邢宇航 李 敏

(火箭軍工程大學(xué) 西安 710025)

(xianxyh404@163.com)

具備初值敏感性和偽隨機(jī)性的混沌系統(tǒng)是非線性的.混沌映射是定義在實數(shù)域上的,然而由于計算精度問題,造成混沌序列有非常短的周期和不動點[1-3].近年來,圖像加密成為了一個研究熱點[4-11],基于混沌的加密算法多用在圖像加密上.但是混沌序列的短周期限制了混沌系統(tǒng)的應(yīng)用[12].解決有限精度的方法[13-18]主要有:一是增大參數(shù)空間;二是構(gòu)造多維混沌系統(tǒng);三是增加擾動;最后一個是增大混沌序列周期.增大參數(shù)空間不能根本上解決有限精度的問題;構(gòu)造多維混沌可以避免不動點問題,但是其穩(wěn)定性和數(shù)字化錯誤仍然存在;擾動可以避免有限精度短周期影響,但是擾動實際上改變了混沌系統(tǒng)的特性.

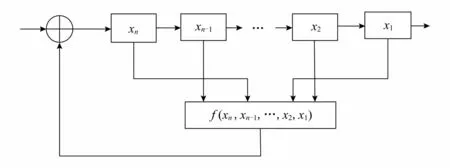
圖1 線性反饋移位寄存器

由于計算精度的影響,混沌映射在迭代過程出現(xiàn)短周期現(xiàn)象.理論上,如果沒有有限精度問題,混沌序列隨機(jī)性是非常好的,但計算機(jī)是有精度要求的.增加擾動的目的也是不讓混沌序列進(jìn)入小周期循環(huán),與其擾動,不如采用高精度,在有限精度內(nèi)重置混沌映射初始狀態(tài).根據(jù)混沌映射初值敏感性,不同的高精度初始值得到的混沌序列不可能相同,利用這樣得到的混沌序列作為加密序列是完全可以實現(xiàn)的.這種設(shè)計既不改變混沌序列本身隨機(jī)特性,也能克服短周期序列的缺陷.同時,盡量在1個混沌序列周期內(nèi)完成對圖像的加密.如果需要加密大量明文圖像,對明文圖像進(jìn)行分組即可保證使用的密鑰流也在1個周期內(nèi).因此,只要確保每次加密使用的密鑰流都在1個周期內(nèi),而且加密不同明文圖像時使用不同的混沌序列,可以保證每次加密都使用不同的密鑰流,而且根據(jù)混沌映射的初值敏感性,不同的初值得到不同的混沌序列,相當(dāng)于一次一密.為了實現(xiàn)這種思想,需要解決混沌映射的初值生成問題,因此,本文設(shè)計由線性反饋移位寄存器(LFSR)狀態(tài)序列作為混沌映射的初值生成算法,每給定一個128b的初值,就可以得到需要的連續(xù)不斷的128b的LFSR狀態(tài)序列,根據(jù)需要加密的明文圖像的需求來決定實際需要多少個128 b密鑰,盡管混沌序列存在短周期,但如果僅僅使用1個周期內(nèi)的密鑰序列,分析者就無法利用短周期的缺陷,從而保證明文圖像的安全.

1 混沌映射初值生成

實際上,每給定一個初始狀態(tài),LFSR都能產(chǎn)生一條偽隨機(jī)序列.當(dāng)初始狀態(tài)固定時,設(shè)計好狀態(tài)轉(zhuǎn)移矩陣,很容易獲得狀態(tài)序列和其任意組合的序列,而且可以獲得非常大周期的偽隨機(jī)序列,LFSR是根據(jù)初始狀態(tài)和狀態(tài)轉(zhuǎn)移矩陣開始工作的.一般地,LFSR包含記憶存儲單元和布爾函數(shù)(反饋函數(shù)),其中反饋函數(shù)是線性的,LFSR的結(jié)構(gòu)如圖1所示.

圖1中,x1,x2,…,xn為寄存器每級存儲單元,(xn,x n-1,…,x1)為移位寄存器的狀態(tài),n級移位寄存器的狀態(tài)總數(shù)為2n個,而f(xn,x n-1,…,x1)是以狀態(tài)中的元素為變量的移位寄存器的反饋函數(shù).當(dāng)移位寄存器的反饋函數(shù)(聯(lián)結(jié)多項式)是本原多項式時,得到的輸出序列就是m序列,m序列具有LFSR的最大周期2n-1,同時序列的隨機(jī)性非常好.根據(jù)移位寄存器的特點,狀態(tài)序列的周期和輸出序列的周期是一樣的.本文則利用這種特性,獲取混沌映射的初始值.給定一個128 b的LFSR的初始狀態(tài),選擇1個本原多項式,就會得到1條最大周期的狀態(tài)序列,把每個狀態(tài)的128b的0,1值,轉(zhuǎn)化為混沌映射的初值.由于混沌映射定義在實數(shù)上,且計算精度最大有16位有效位,把128b的狀態(tài)均分成32 b,然后轉(zhuǎn)化為實數(shù),作為混沌映射初值的小數(shù)部分,其整數(shù)部分為0,從而可以做成混沌映射的4個初始值.由于狀態(tài)序列的周期足夠大,可以保證得到連續(xù)不斷的初始值來構(gòu)造混沌序列,且由于LFSR的1步平移特性,連續(xù)的狀態(tài)不會出現(xiàn)重復(fù),加上混沌映射的初值敏感性,得到的混沌序列也不會發(fā)生重復(fù).具體的初始值生成方法如下:

1)選擇LFSR的初始狀態(tài)(即初始密鑰)產(chǎn)生并記下狀態(tài),不失一般性,產(chǎn)生的T個時刻的狀態(tài)序列記為,并把每個狀態(tài)均分為4組x1i,x2i,x3i,x4i,即

si=(x1i,x2i,x3i,x4i),0≤i≤T.

2)記x1i,x2i,x3i,x4i對應(yīng)的混沌映射的初始值為x1(i),x2(i),x3(i),x4(i),混沌映射初始值計算方式為:

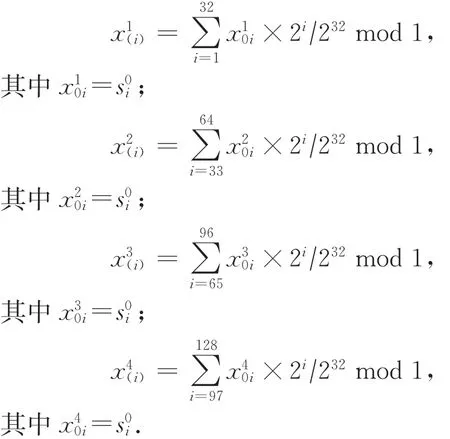
2 圖像加密方案

2.1 圖像置亂

一般地,圖像加密有2個過程.第1個過程是置亂[19],對需要加密的圖像像素進(jìn)行混亂,消除圖像像素之間的相關(guān)性,常用的辦法是利用線性變換,即置換.原始圖像的相鄰像素的極大相關(guān)性會降低直接加密的安全性.本文采用對明文圖像像素進(jìn)行置換,即重新排序,為了增加置換對圖像加密的安全性保護(hù),這里同樣采用混沌映射來設(shè)計置換函數(shù),線性置換的實現(xiàn)思路如下所述:

1)根據(jù)明文圖像實際大小情況,首先計算圖像像素和像素個數(shù).如果是60×60的灰度圖像,那么總的像素個數(shù)就是3600.

2)利用第1個混沌映射初值產(chǎn)生1條混沌序列,任意截取3 600長度的混沌序列值,并按大小順序?qū)煦缧蛄羞M(jìn)行排序.

3)利用步驟2)的排序結(jié)果作為明文圖像像素的置換表,然后對明文像素進(jìn)行新的排序和置亂.

4)把置亂后的圖像保存即為置亂后的結(jié)果.

2.2圖像擴(kuò)散

實際上,根據(jù)2.1節(jié)的變換結(jié)果,像素已經(jīng)得到了有效置亂.仿真結(jié)果表明,經(jīng)過置亂,明文圖像的相鄰像素相關(guān)性已被打破,但這是一個線性變換,考慮明文圖像的安全性,需要對明文圖像實現(xiàn)擴(kuò)散變換,即非線性變換.顯然,這里用混沌序列對已置亂的圖像進(jìn)行加密變換.文中利用余下的3個混沌映射初值生成3條混沌序列,利用混沌序列對像素進(jìn)行加密變換.具體的圖像擴(kuò)散過程如下:

1)根據(jù)需要加密的明文圖像大小,首先計算像素和像素個數(shù).如果是60×60的灰度圖像,那么總的像素個數(shù)就是3600.

2)利用后3個混沌映射初值產(chǎn)生3條1個周期內(nèi)的混沌序列,在1個周期內(nèi)任意截取并保留每條序列3600×8個混沌序列值.

3)由于像素都是0～255之間的值,通過轉(zhuǎn)化把每條序列3600×8個混沌序列值轉(zhuǎn)化為0～255之間的值,然后建立3個混沌矩陣依次與像素值進(jìn)行模256加運算,獲得最終的矩陣值,即新的像素值.

4)把擴(kuò)散后的圖像保存即為加密后的密文圖像.

2.3 加密算法

算法1.加密算法.

輸入:明文圖像P1,P2,…,P T,混沌映射及參數(shù);

輸出:密文圖像P′1,P′2,…,P′T.

步驟:

1)計算明文圖像P1尺寸M1×N1,同時建立圖像像素矩陣;

2)選擇LFSR的初始狀態(tài)(即初始密鑰)產(chǎn)生并記下狀態(tài),任意選擇第t1時刻LFSR狀態(tài)記為st1,并把st1均分為4組,x1i,x2i,x3i,x4i,每組32b,即

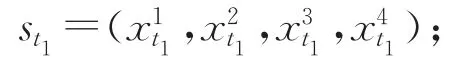
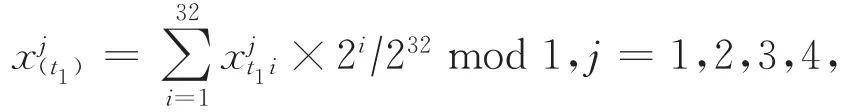
利用初始值x1(t1)得到混沌序列A1,截取任意M1×N1長混沌序列,根據(jù)大小排序建立混沌置換矩陣;

4)根據(jù)混沌置換矩陣把明文圖像P1像素矩陣置亂得到P11;

5)利用混沌初值x2(t1),x3(t1),x4(t1)得到3條混沌序列A2,A3,A4,截取任意3條M1×N1長混沌序列,并把混沌實數(shù)序列二進(jìn)制量化后與像素矩陣P11進(jìn)行按位模加;

6)輸出密文圖像P′1;

7)利用上述加密思路,選擇st2,st3,…,stT分別實現(xiàn)對明文圖像P2,…,P T的加密,得到密文圖像P′2,…,P′T.

實際上,算法1中的混沌映射的初值生成可以在預(yù)處理過程完成,對不同明文圖像的加密可以并行進(jìn)行運算,從而提高加密的效率.

3 實驗和仿真

根據(jù)第2節(jié)的加密方案,算法的參數(shù)選擇如下:

LFSR選擇的是128級的移位寄存器,移位寄存器的生成多項式是128級的本原多項式

f(x)=x128+x29+x27+x2+1,初始密鑰為:

不失一般性,本原多項式產(chǎn)生的移位寄存器序列的第1個狀態(tài)即為初始密鑰.實際應(yīng)用時,可以從狀態(tài)周期序列中任意時刻截取.

混沌映射函數(shù)選擇Tent映射,其函數(shù)表達(dá)式如下所示:

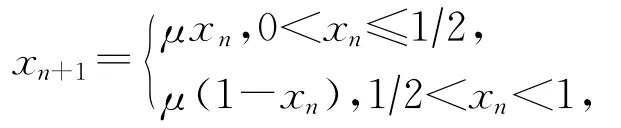
這里取μ=1.9.混沌映射初值按下列方式獲取:

是混沌映射的初值,由其得到的混沌序列用于明文圖像置亂,也是混沌映射的初值,其獲得的混沌序列作為圖像擴(kuò)散過程的加密密鑰.Tent映射具有較好的遍歷均勻性,是應(yīng)用較為廣泛的混沌映射之一,且易于實現(xiàn)和運算速度快.本文正是基于此,選擇此映射作為加密方案的混沌映射算法.在實驗中,對Tent映射的輸出進(jìn)行二進(jìn)制量化時采用的是常規(guī)的量化函數(shù):

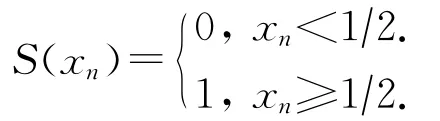
仿真結(jié)果是以1幅圖像為例,在Matlab環(huán)境中進(jìn)行,采用雙精度實數(shù)進(jìn)行實驗.

3.1 圖像置亂實驗結(jié)果

圖2是圖像置亂實驗結(jié)果:經(jīng)過置亂,像素得到重新排序后,已無法識別出原圖像的特征,也就是說,從置亂后的圖像無法直接獲取原始圖像的信息.如果想從置亂后的圖像恢復(fù)原始圖像,必須找到置亂矩陣,即混沌序列;或者利用窮舉的辦法,遍歷所有的(256×256)!個置換.

圖2 明文圖像置亂對比圖

圖3 明文圖像加解密對比圖

3.2 圖像擴(kuò)散實驗結(jié)果

圖3是明文圖像加解密實驗結(jié)果,加解密效果較好.明文圖像經(jīng)過3個混沌序列加密后,不能從明文圖像獲得原始圖像的信息.同時,由于3條混沌序列的初值不同,再根據(jù)混沌映射的初值敏感性,3條混沌加密序列是相互獨立的,這樣保證了初值的密鑰空間足夠大.只有獲得3個初值,才有可能恢復(fù)出明文圖像.同時,由于加密圖像的混沌序列都在1個周期內(nèi),通過統(tǒng)計尋找明密文的規(guī)律是不現(xiàn)實的,如果一次加密的明文圖像數(shù)量大時,又改變了使用的混沌初值,更無統(tǒng)計規(guī)律可言,即使個別密文被破譯,也不會影響其他明文圖像的安全.

3.3 圖像直方圖測試

圖4是明文直方圖和密文直方圖的比較結(jié)果,顯然,經(jīng)過加密后,明文直方圖得到了明顯的改變,明文直方圖的顯著特征在密文圖像中都不存在,密文直方圖分布比較均勻,使得通過統(tǒng)計直方圖尋求明文特征的統(tǒng)計攻擊變得困難,能夠抵抗統(tǒng)計攻擊.

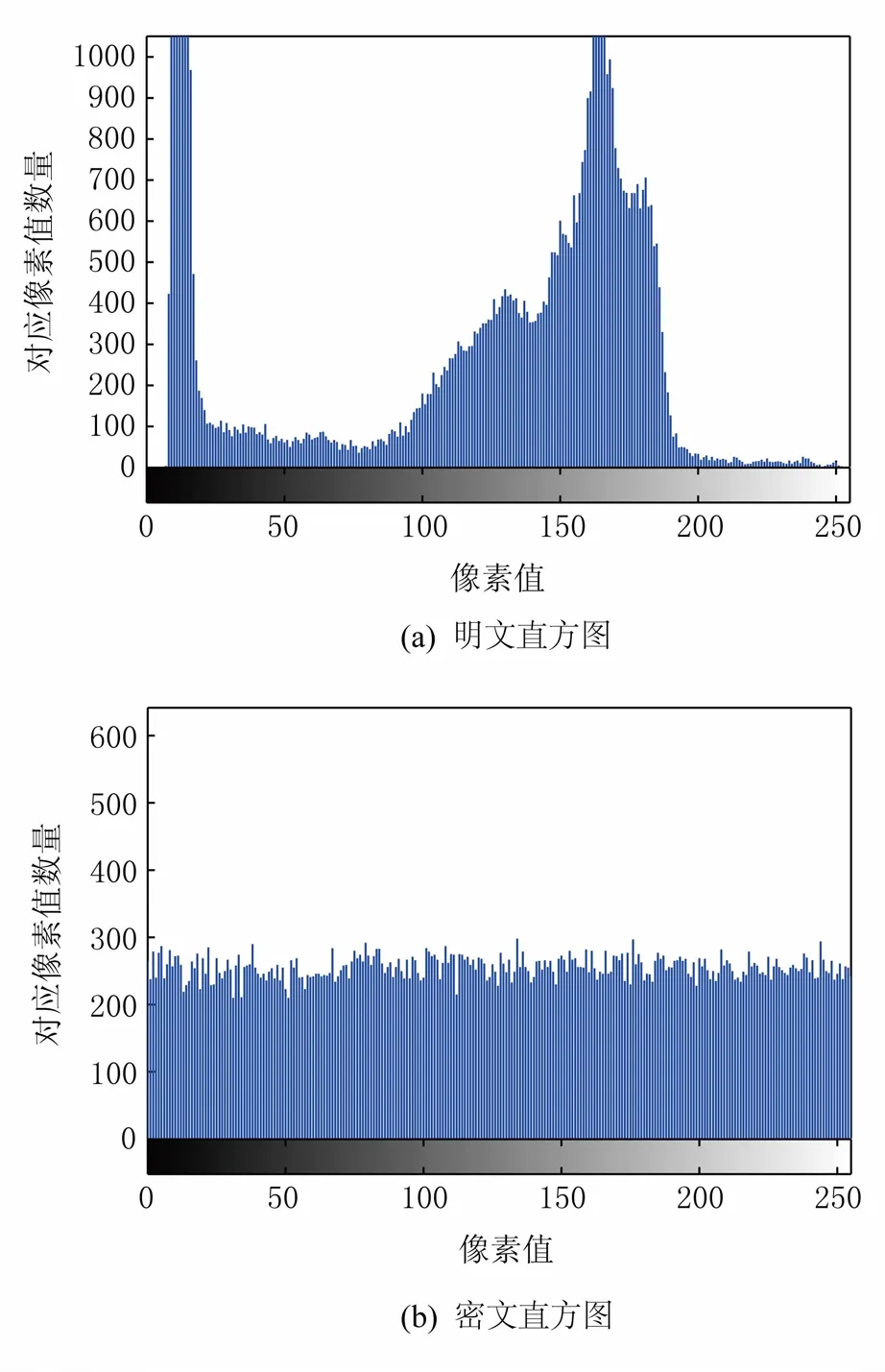
圖4 明密文圖像直方圖對比

3.4 相關(guān)性測試

圖5是圖像的對角相關(guān)性實驗結(jié)果:經(jīng)過加密的圖像的對角方向相關(guān)性明顯降低,相關(guān)性值的分布非常均勻,表明經(jīng)過加密后,對角方向上像素的相關(guān)性得到了降低,不能從密文圖像的像素相關(guān)性來找明文的像素相關(guān)性.同理,水平和垂直方向的相關(guān)性亦有同樣的結(jié)果.

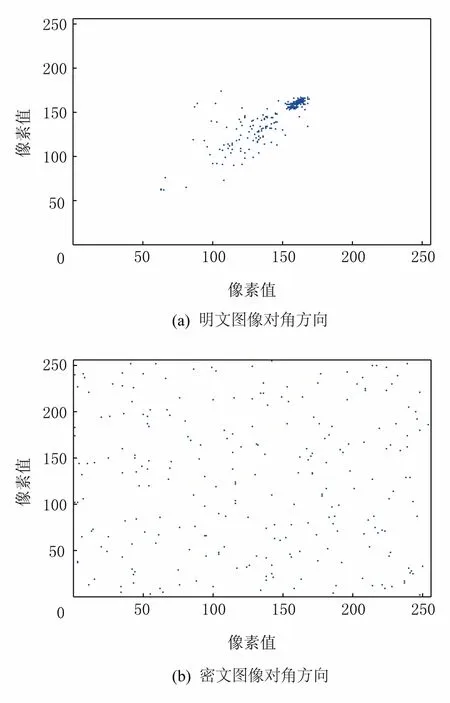
圖5 明密文圖像對角像素分布對比

3.5 密鑰空間分析

密鑰空間大小是衡量算法安全性的重要指標(biāo),其可以直觀看出算法能否抵抗窮舉攻擊.本文加密方案中的混沌映射的初值x1(i),x2(i),x3(i),x4(i)生成的混沌序列相互獨立,因此,LFSR的初始密鑰的長度是128b,整個方案的密鑰空間就是2128,能夠抵抗窮舉攻擊.

4 結(jié) 論

本文提出了一個針對批圖像處理的混沌序列加密方案,該方案可以克服混沌加密系統(tǒng)密鑰空間小和有限精度問題,保持混沌映射的特點,利用混沌映射的初值敏感特點,通過設(shè)計混沌映射初值,進(jìn)而實現(xiàn)混沌加密方案的設(shè)計.為了保證混沌加密系統(tǒng)的安全性,初值生成利用了LFSR的128 b狀態(tài)序列,保證了初值生成過程的安全性.為了消除混沌系統(tǒng)的短周期問題,在對明文圖像進(jìn)行加密時,采用了一次一密的思想,并利用多輪混沌加密的思想,在保證密鑰空間足夠大的同時,使得密鑰和明文進(jìn)行充分混合,進(jìn)而達(dá)到擴(kuò)散的目的.同時,初值生成算法可以獲得連續(xù)的不同的密鑰序列,可以對大量圖像進(jìn)行并行加密操作,實現(xiàn)了圖像的批加密功能.又由于每幅圖像加密的密鑰序列均不相同且僅使用1個周期內(nèi)的混沌序列進(jìn)行加密,達(dá)到了一次一密的加密效果,保證了明文圖像的安全性.

[1]Li Chunhu,Luo Guangchun,Qin Ke.An image encryption scheme based on chaotic tent map[J].Nonlinear Dynamics,2017,87(1):127-133

[2]Huang X L.Image encryption algorithm using chaotic Chebyshev generator[J].Nonlinear Dynamics,2012,67:2411-2417

[3]胡英輝,羅軍,蘇輝.一種改善混沌序列有限精度效應(yīng)的新方法[J].系統(tǒng)仿真學(xué)報,2012,24(11):2349-2352

[4]翟依依,王光義.基于Tent混沌序列的數(shù)字圖像加密方法[J].現(xiàn)代電子技術(shù),2014,37(12):73-77

[5]Li J,Li X,Yang B,et al.Segmentation-based image copymove forgery detection scheme[J].IEEE Trans on Information:Forensics Security,2015,10(3):507-518

[6]Sui Liansheng,Xin Meiting,Tian Ailing.Multiple-image encryption based on phase mask multiplexing in fractional fourier transform domain[J].Optics Letters,2013,38(11):1996-1998

[7]Sui L,Gao B.Single-channel color image encryption based on iterative fractional fourier transform and chaos[J].Optics Laser Technology,2013,48(7):117-127

[8]Abuturab M R.Security enhancement of color image cryptosystem by optical interference principle and spiral phase encoding[J].Application Optics,2013,52(8):1555-1563

[9]Volos C,Kyprianidis I,Stouboulos I.Image encryption process based on chaotic synchronization phenomena[J].Signal Process,2013,93(5):1328-1340

[10]Wang X,Teng L,Qin X.A novel colour image encryption algorithm based on chaos[J].Signal Process,2012,92(4):1101-1108

[11]Li Xiaowei,Li Chengqing,Lee In-Kwon.Chaotic image encryption using pseudo-random masks and pixel mapping[J].Signal Process,2016,12(5):48-63

[12]劉嘉輝,張宏莉.基于可擴(kuò)展精度的Logistic混沌隨機(jī)序列的并行計算方法[J].2011,41(9):834-845

[13]張永紅,張博.一種改善混沌序列有限精度效應(yīng)的新方法[J].計算機(jī)應(yīng)用研究,2015,32(6):1770-1773

[14]Akhshani A,Akhavan A,Lim S-C,et al.An image encryption scheme based on quantum logistic map[J].Communications in Nonliner Science and Numerical Simulation,2012,17(12):4653-4661

[15]Zhang W,Wong K,Yu W,et al.An image encryption scheme using reverse 2-dimensional chaotic map and dependent diffusion[J].Communications in Nonliner Science and Numerical Simulation,2013,18(8):2066-2080

[16]El-Latif,Li L,Wang N,et al.A new approach to chaotic image encryption based on quantum chaotic system,exploiting color spaces[J].Signal Process,2013,93(11):2986-3000

[17]何朗日,李萍,陳水華.基于m序列持續(xù)擾動Logistic混沌序列的視頻加密及FPGA實現(xiàn)[J].激光雜志,2015,36(9):56-59

[18]Papamarkou T,Lawrance A J.Nonlinear dynamics of trajectories generated by fully-stretching piecewise linear maps[J].International Journal Bifurcat Chaos,2014,24(5):1450071

[19]朱曉升,廖曉峰.基于圖像分區(qū)的置亂算法[J].計算機(jī)技術(shù)與發(fā)展,2015,25(12):52-55