Guanghui Qing·Junhui Mao·Yanhong Liu

1 Introduction

In standard finite element displacement methods,the displacements are usually computed first,then the stresses or/and strains are calculated by numerically differentiating,based upon the constitutive relations and compatible equations at element level,usually resulting in loss of accuracy.Meanwhile,the values of the strain component computed from different elements connected at a node are different.Consequently,a smoothing or recovery procedure for nodal stresses may be carried out over the local or whole finite element domain.The boundary nodal stresses obtained from such finite element analysis are inconsistent with the prescribed stresses in displacement methods[1,2].

For equilibrium finite element methods,stresses are equilibrated within the element and tractions are balanced at interelement boundaries.However,equilibrium methods have been found to have limited use in general-purpose computer codes because of their behavior without judicious choice of basis functions[2].

Numerous mathematical models result from physical problems in the form of systems of partial differential equations involving several physically disparate quantities that need to be approximated simultaneously.The finite element approximations of such problems are well known as mixed finite element methods.Generally,the dual variable is computed as a fundamental unknown in mixed methods.Early contributions towards mixed methods can be found in Refs.[3–10].More recent developments can be found in Refs.[11–25].As a class of numerical methods,mixed models are widely used in the field of fluid mechanics;For example,displacement models are impractical for the Stokes problem.For such problems,mixed methods represent the simplest and most direct alternative[25].Several main advantages and disadvantages of mixed methods can be summarized as follows:

(1)Linear interpolation functions are often sufficient to give satisfactory results for practical applications.Boundary and interelement conditions can be represented properly,and no difficulties arise due to higher derivatives;

(2)The stress or strain variables,as the main design parameters of a structure,are the direct results of the finite element governing equation without requiring differentiation of displacements.This is also advantageous for physically nonlinear analysis,in which yield conditions etc.are expressed in terms of stresses[8,11];

(3)It is well known that,for nearly incompressible and incompressible materials,finite element computations based on the standard displacement formulation fail due to the onset of the locking phenomenon.Classical mixed formulations are a valid alternative to locking-affected methods,since they provide mathematical models capable of treating both compressible and incompressible elasticity problems in a unified framework[8,26];

(4)Compared with displacement methods,the mathematical theory of mixed methods is relatively complex.For mixed methods based on the Hellinger–Reissner(H–R)variational principle alone,stability is paramount.The stability of numerical results is related to the invertibility of the coefficient matrix of the finite element governing equation.A main drawback of mixed methods is the indefiniteness of the resulting system matrix[20].It is not easy to construct a pair of finite elements for the displacement vector and symmetric stress tensor which satisfies the stability conditions of Brezzi’s theory[4].

Some representative studies on mixed methods published in recent years should be mentioned here:Arnold and Winther[16]suggested some stable elements for a two dimensional problem,while the corresponding method in three-dimensional space was first characterized by Adams and Cockburn[17],and thorough analyses of the finite elements were provided in Ref.[19].The construction of these elements is not convenient for computer programs, since they are of high polynomial order,implying high cost even for the lowest-order scheme.A family of symmetric tensor-valued finite elements of arbitrary order was constructed using the tangential-displacement normal-normal-stress(TDNNS)formulation in Ref.[10].However,the mathematical theory and the process of construction of the TDNNS formulation are not simple and not suitable for engineers.

No doubt,some open questions remain in connection with displacement methods,equilibrium methods,and mixed methods for two-or three-dimensional elasticity problems.For mixed methods,some questions of stable elements require further study.

The objective of this work is to propose two simple generalized mixed methods without any stable element schemes but with automatically stable numerical results.

2 Variational principles for elasticity

Consider a body under static loading.The body occupies the volumeV.Sis the surface of the body.S=Su∪Sσ,whereSuandSσare the segments ofSwhere displacements and surface tractions are prescribed,respectively;the outward unit normal onSis denoted byN≡ni.Let?be the gradient operator in the deformed body which,under the assumption of infinitesimal deformation,is indistinguishable from the deformed body.

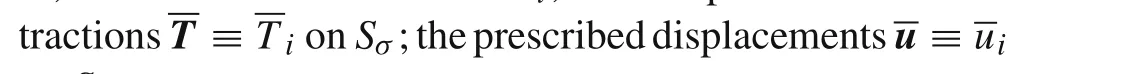
Assuming the displacement boundary conditionsu?u=0 is satisfied a priori for all variational principles in the following.

The minimum potential energy principle for elasticity problems has the form

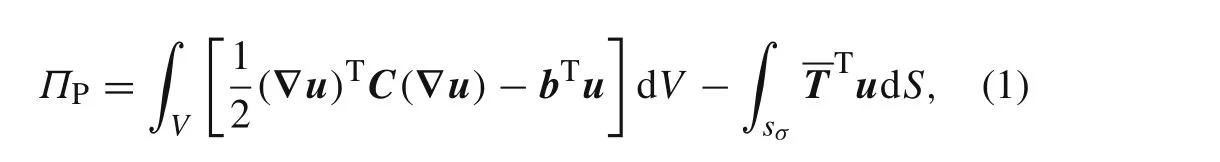
whereCis the symmetric stiffness matrix of a material.

The H–variational principle [27] for elasticity problems contains both displacement and stress fields

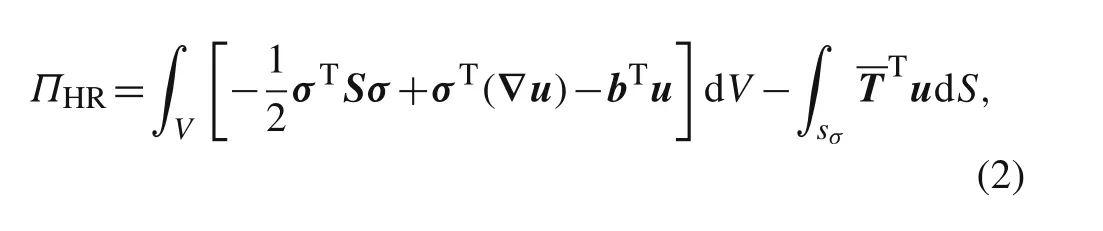
whereS=C?1is the compliance matrix.

Like the H–R variational principle,there are also both displacement and stress fields in the generalized variational principle[28].This principle can be expressed in the following form

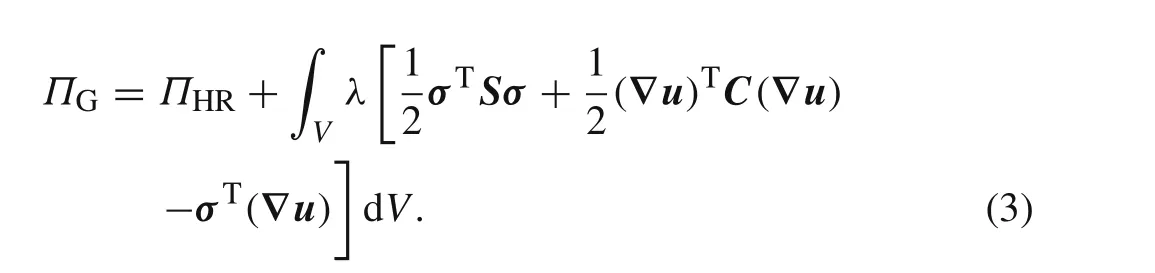
It should be pointed out that Felippa[29,30]constructed a one-parameter family of mixed variational principles for linear elasticity in 1989.Equation(3)is such a one-parameter family of mixed variational principles.

Generally,we expect to take 0?λ?1 in Eq.(3).Values of the parameterλ＜0 orλ＞1 are not of practical interest.It is clear that,lettingλ=0,Eq.(3)becomes the H–R variational principle.Meanwhile,lettingλ=1,one obtains the minimum potential energy principle in Eq.(1).

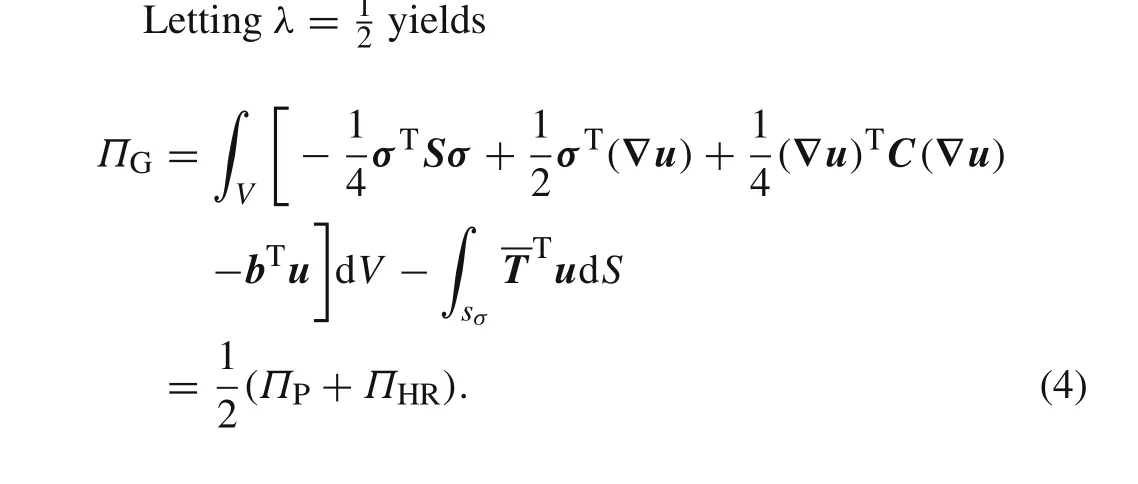
It is interesting that the generalized variational principle above is one-half of the sum of the minimum potential energy principle and H–R variational principle.Our practice shows that,indeed,only forλ=1/2 can good accuracy and stability of the generalized mixed method be obtained.

Note that the H–R variational principle in Eq.(2)and generalized variational principle in Eq.(4)are the principles of stationarity.For the principles in Eqs.(2)and(4),the nonvariational constraint is the constitutive relations.The equilibrium equations,the tractions boundary condition can be satisfied a posteriori.

3 Element formulations

3.1 Compatible mixed element formulations

Without loss of generality,consider first ann-node compatible linear element for 3D problems.Both the displacement vectoruand stress vectorσare expressed using the same shape functions

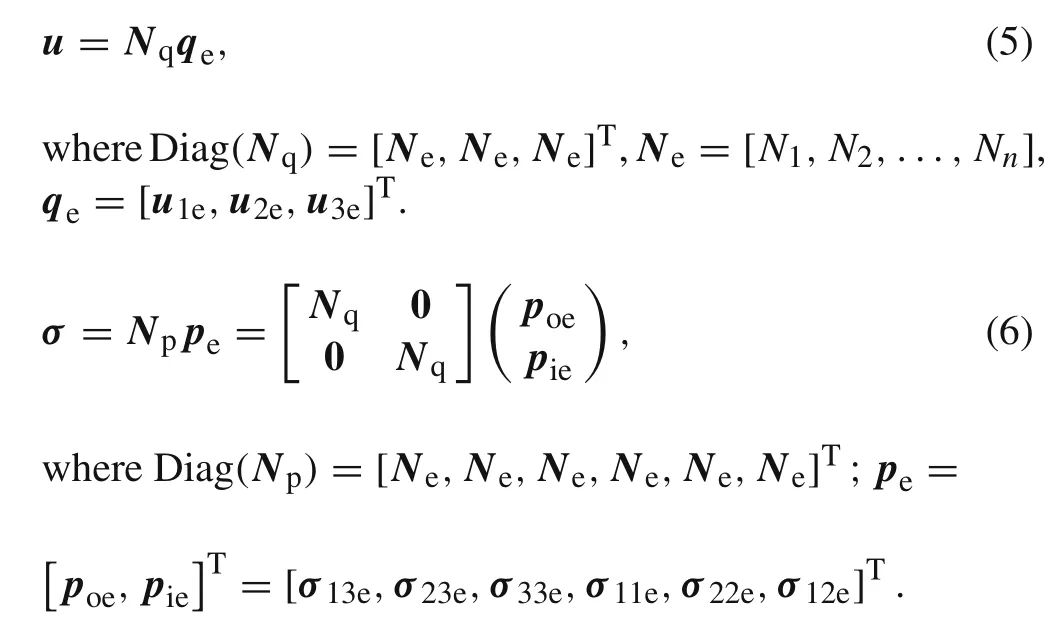
It is well known that,inserting Eqs.(5)and(6)into Eq.(2)and performing the energy integration,one obtains the discrete form of the H–R variational principle

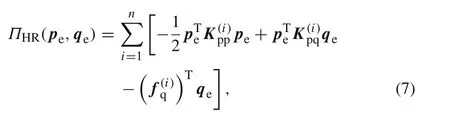
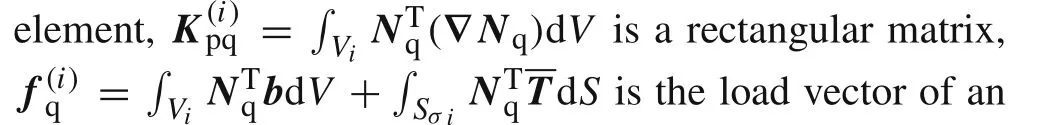
In what follows,the superscript“i”will be dropped for clarity.

Considerpeandqeas independent variables.ByδΠHR(pe,qe)=0,one has two Euler–Lagrange(EL)equations

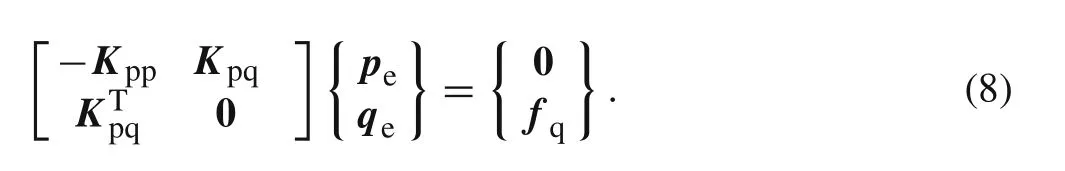
It can be seen that the classical formulation in Eq.(8)resulting from the H–R variational principle of various physical problems is symmetric,but it possesses zeros on the diagonal.Indeed,the coefficient matrix of Eq.(8)is non-positive definite.If stable elements[16,20,26]are not employed,it is very difficult to obtain stable solutions directly from Eq.(8).

3.2 Compatible displacement element formulations

In the same way,using Eq.(5),the discrete form of the minimum potential energy principle in Eq.(1)is

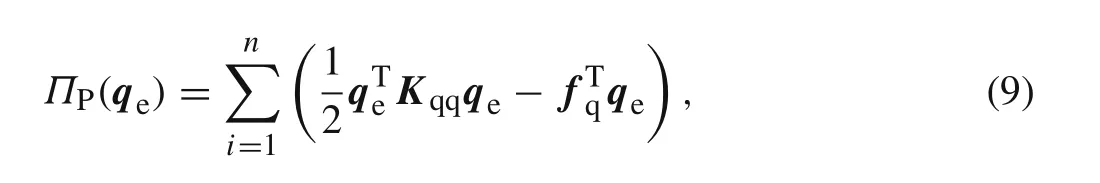
3.3 Compatible generalized mixed element formulations

It is of interest to see that adding Eq.(10)to the second equation of Eq.(8)yields

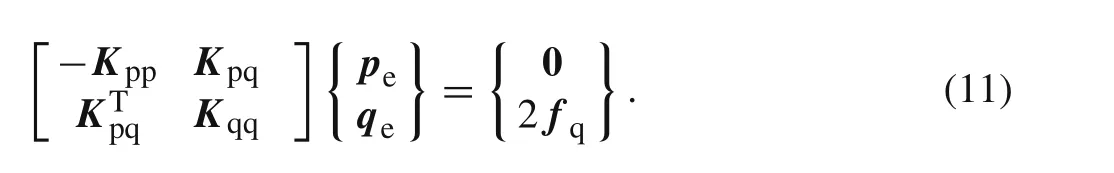
In the above equation,the coefficient matrix is not only symmetric,but also there are no zeros on the diagonal.This is a main difference from Eq.(8).Equation(11)is termed the compatible generalized mixed element with 8 nodes(CGME8)for 3D problems in this work.

Certainly,Eq.(11)can be proved by the generalized variational principle in Eq.(4).Using Eqs.(5)and(6),the discrete form of Eq.(4)can be written as

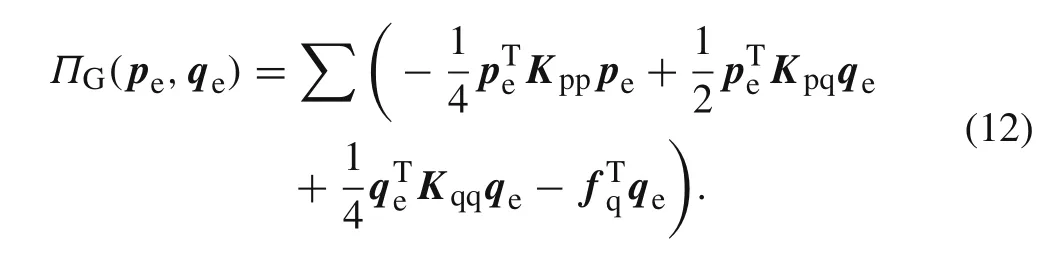
In Eq.(12),the integral expressions ofKpp,Kpq,andfqare the same as those in Eq.(7),respectively;the integral expressionKqqis identical to theKqqin Eq.(9).

Taking the variation of Eq.(12)with respect to variablespeandqeleads immediately to Eq.(11).

The summation of Eq.(11)on all elements gives a novel algebraic system for finite element analysis

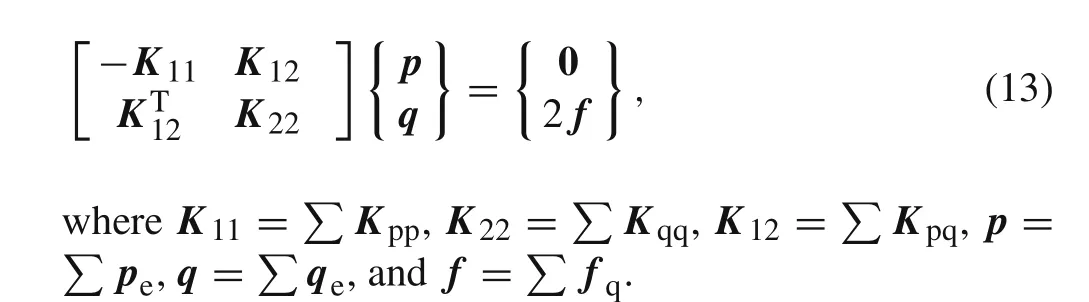
In general,at system level,the whole coefficient matrix has a structure equivalent to that of an element.It is clear that the coefficient matrix of Eq.(13)is characterized by symmetry with respect to the stress and displacement variables of all nodes.Certainly,the coefficient matrix of Eq.(13)is invertible,which implies that its numerical results will be stable[26,31].

3.4 Noncompatible generalized mixed element formulations

On the basis of Refs.[32,33],for a noncompatible element,the element displacementucan be expressed as a sum of the compatible partNqqeand the noncompatible partNrre

Here,Nris the shape function matrix with respect to points within elements;reis the displacement vector corresponding to points within elements.

In a similar way,substituting Eq.(14)into Eq.(1)results in

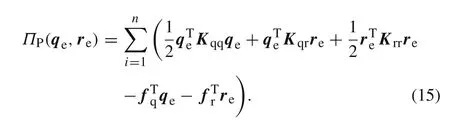
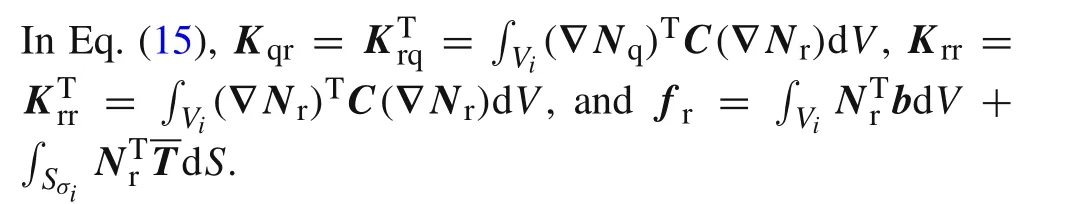
The result of the variation of Eq.(15)with respect toreis given by

Here,Krris an invertible matrix[32,33].From this,one obtains

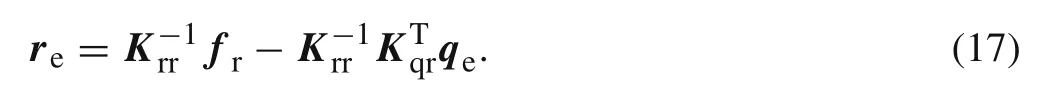
Eliminatingrein Eq.(15)using Eq.(17),the following EL equation can be derived from the new form of Eq.(15)

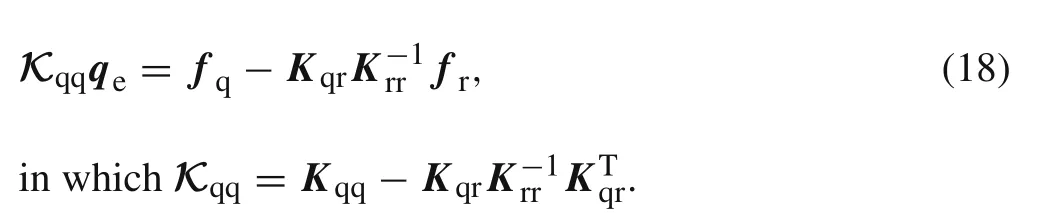
In a similar way,on substitution of Eqs.(6)and(14)into Eq.(2),the resulting noncompatible finite element functional has the form

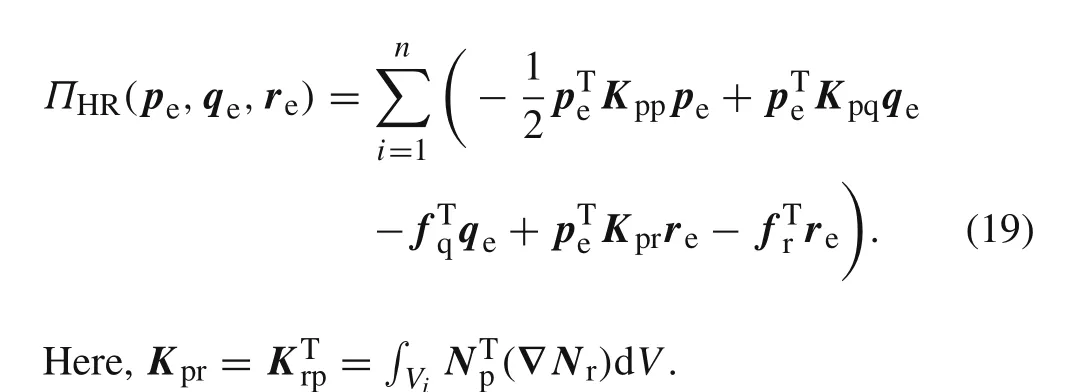
Using Eq.(17),one can also eliminaterefrom the above equation to yield

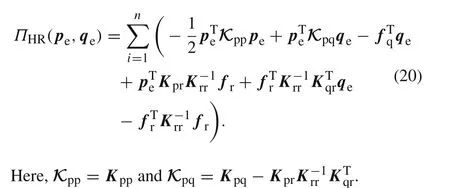
Considering the combination of the result ofδΠHR(pe,qe)= 0 of Eq.(20)with respect topeand Eq.(18),one has

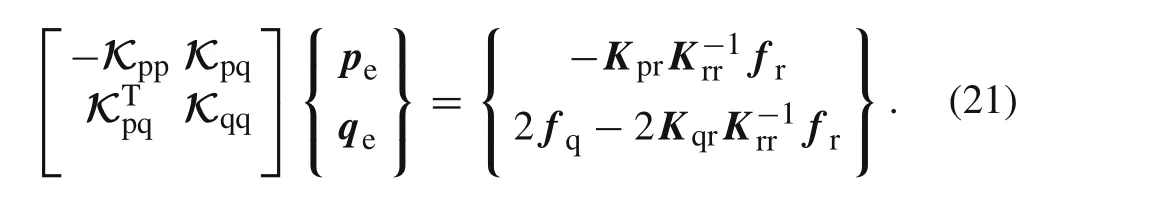
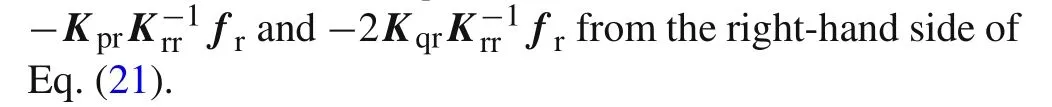
Therefore,the simplified noncompatible generalized mixed element with 8 nodes(NCGME8)for 3D problems is given by

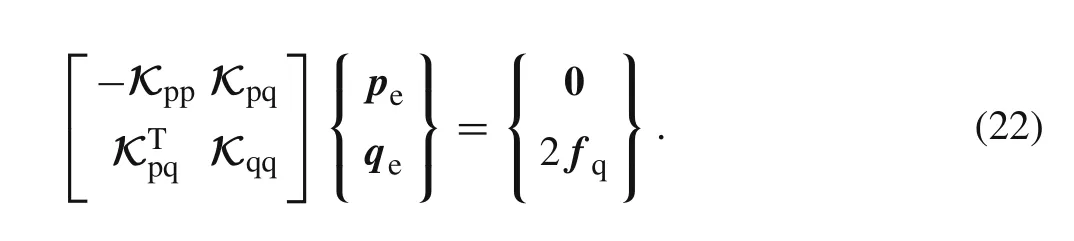
The algebraic system for the finite element analysis corresponding to Eq.(22)has the form

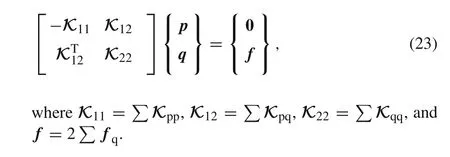
4 Imposing boundary conditions

For common finite element problems with prescribed but nonzero values atvarious locations,one approach in practice is to add a large number or penalty term,for instance 1020,to the leading diagonal of the stiffness matrix in the row corresponding to the prescribed value.The term in the same row of the right-hand side vector is then set to the prescribed value multiplied by the augmented stiffness coefficient[33].

Such a procedure is only successful if small terms are indeed very small relative to 1020.Another prerequisite may be required,i.e.,that the coefficient matrix of the algebraic system is a bandwidth matrix.Our practice shows that this procedure is not suitable for Eqs.(13)and(23),which involve known nonzero stress values(e.g.,the prescribed surface tractions)since the submatrixK12in Eq.(13)orK12in Eq.(23)is not a zero matrix.

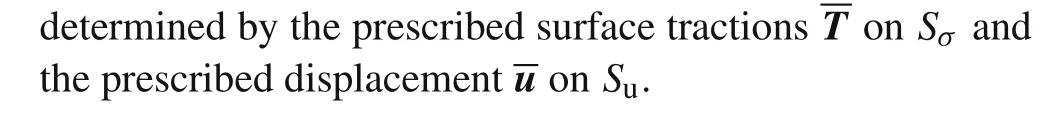
Taking Eq.(23)as an example,interchanging rows and columns,it can be recast into the following form

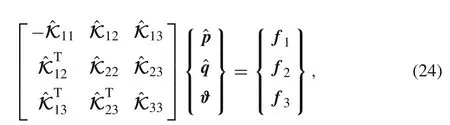
Therefore,one has

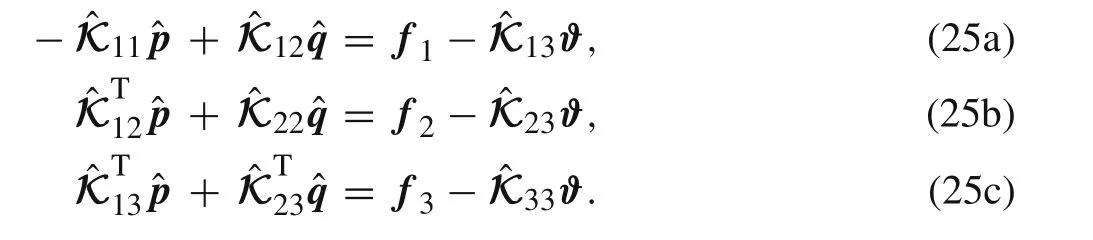
Of course,Eq.(25c)is redundant.Consequently,the final governing equation for the solutions of unknown nodal displacements and stresses is

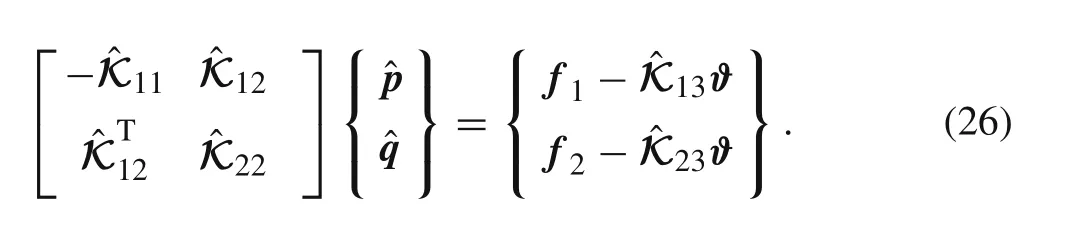
The simple technique presented above for imposing stress and displacement boundary conditions is employed in our program.In the next section,numerical examples show that the boundary nodal stresses are consistent with the prescribed stresses onSσ.

5 Numerical examples and discussion

5.1 A thick rectangular plate with simply supported edges

Consider a thick rectangular plate with in-plane dimensionsa=b=1.0 and total thicknessh=0.10(Fig.1).Here,we assume that the edgesx=0,aandy=0,bare simply supported,and use material propertiesE11=10E22=10E33,G12=G13=0.6E33,G23=0.5E33,andν12=ν13=ν23=0.25.Uniform normal load of 1.0 is applied on the upper surface of the plate[34].

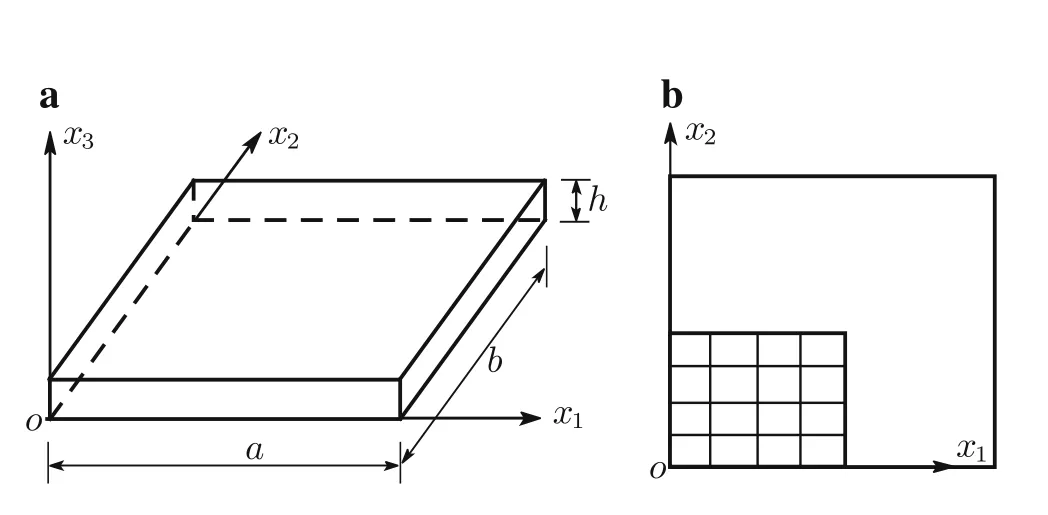
Fig.1 A thick rectangular plate

Using the symmetry about thex1-andx2-axes,only one quarter of the plate(Fig.1b)is analyzed with uniform meshes.The convergence rate and accuracy of displacements and stresses at specific locations are depicted in Figs.2–12.The results for the noncompatible displacement element with 8 nodes(NCDE8)were obtained using commercially available software ABAQUS?.

For Figs.2–10,Table 1 presents the size of each mesh using the notationl×mforlsubdivisions along thex1-axis andmsubdivisions along thex2-axis with the same type of elements,with four subdivisions in thex3direction for all models.

On the basis of the results for the 12×12×4 mesh,the errors presented in the legends to Figs.2–10 were computed using the formula(Exact? Numerical)/Exact× 100%.

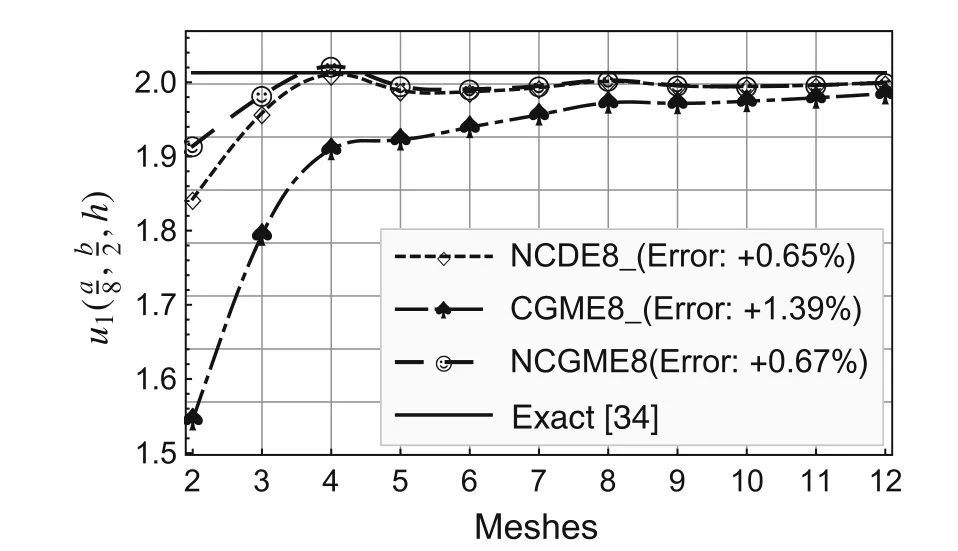
Fig.2 Comparison of displacement

Fig.3 Comparison of displacement

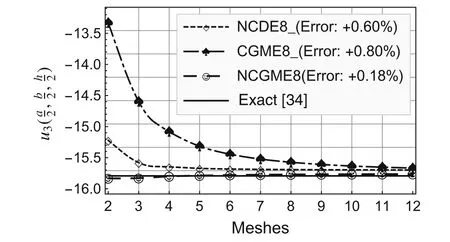
Fig.4 Comparison of displacement

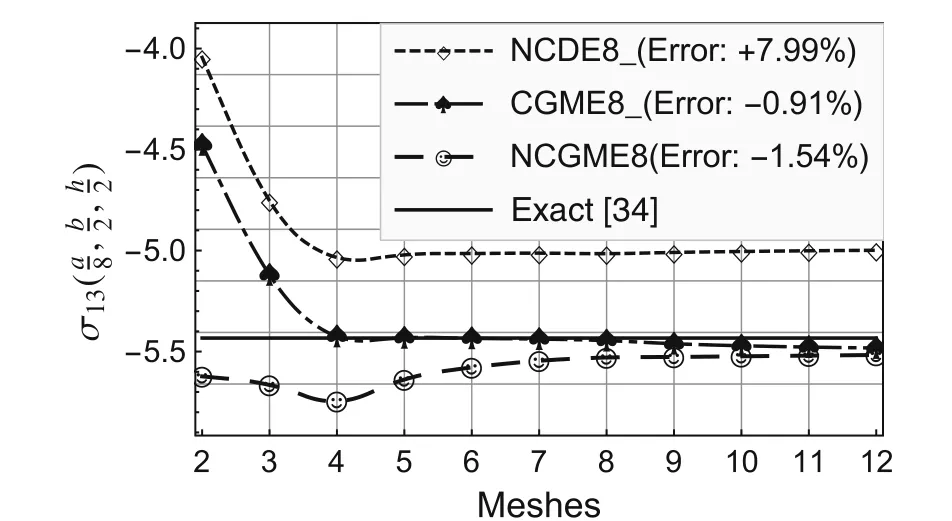
Fig.5 Comparison of stress

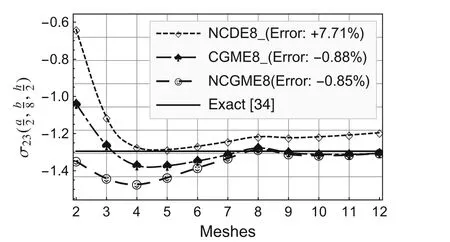
Fig.6 Comparison of stress

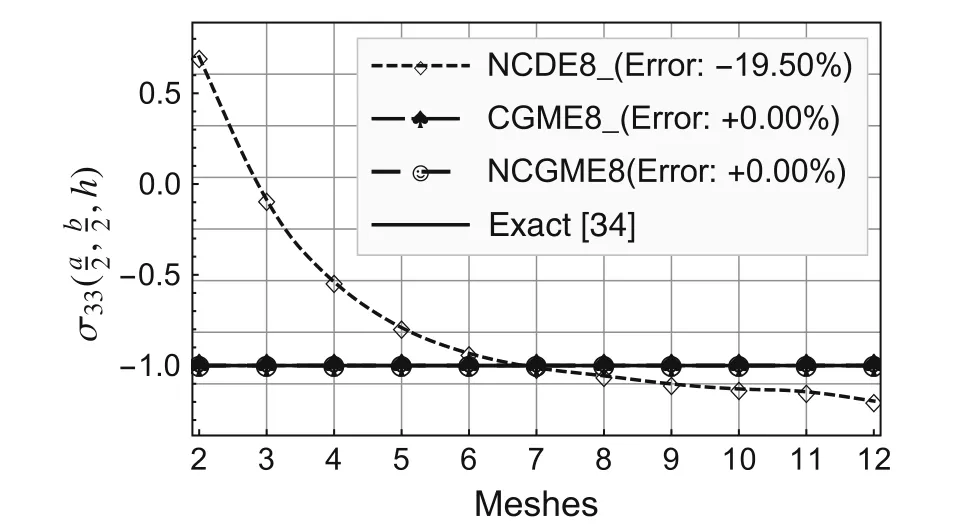
Fig.7 Comparison of stress

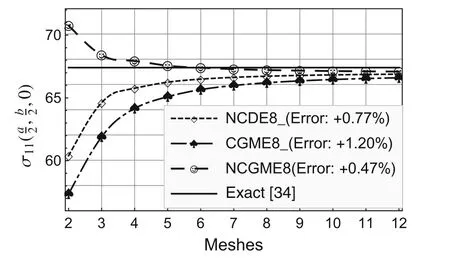
Fig.8 Comparison of stress

In the present computer program,two Gauss quadrature points in each direction were employed for CGME8 and NCGME8.

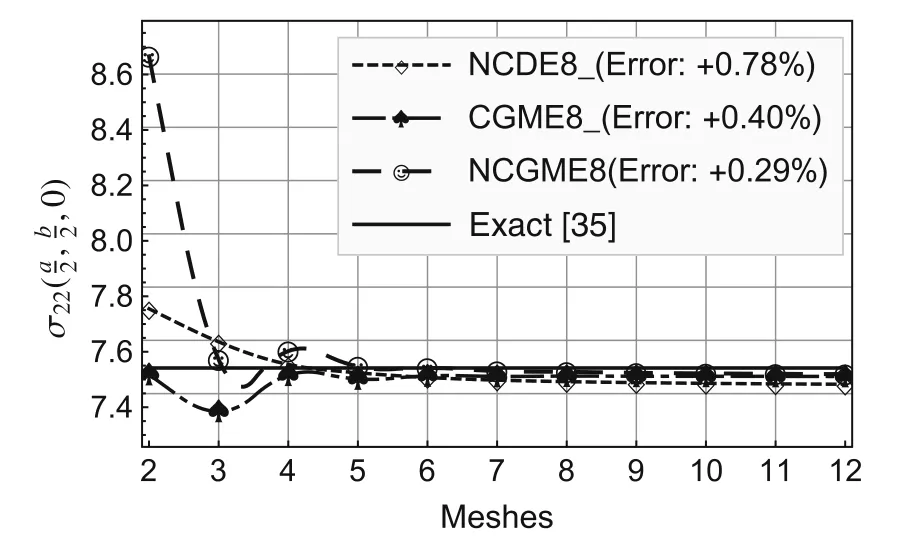
Fig.9 Comparison of stress

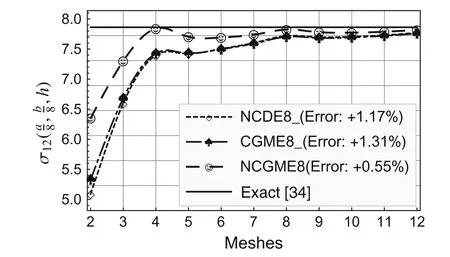
Fig.10 Comparison of stress

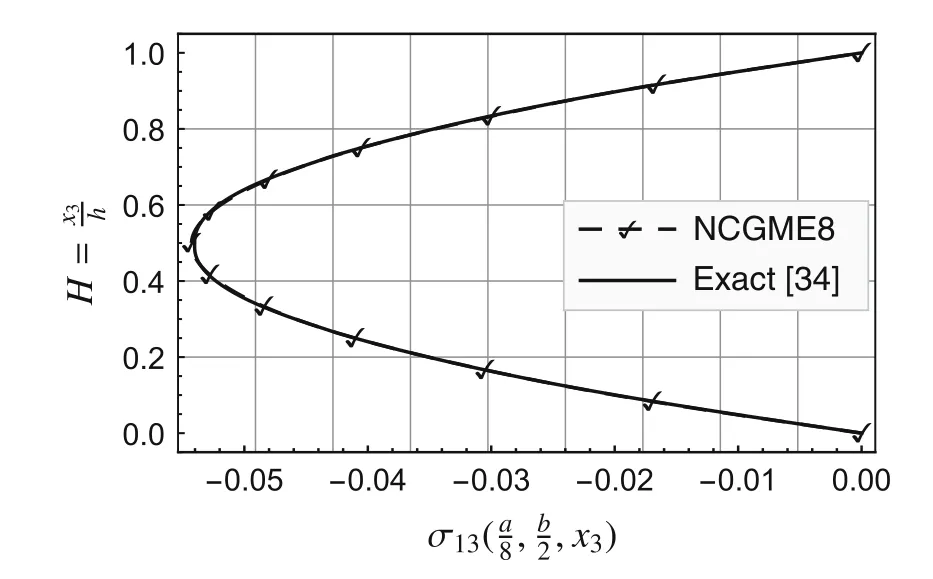
Fig.11 Distribution along thickness of

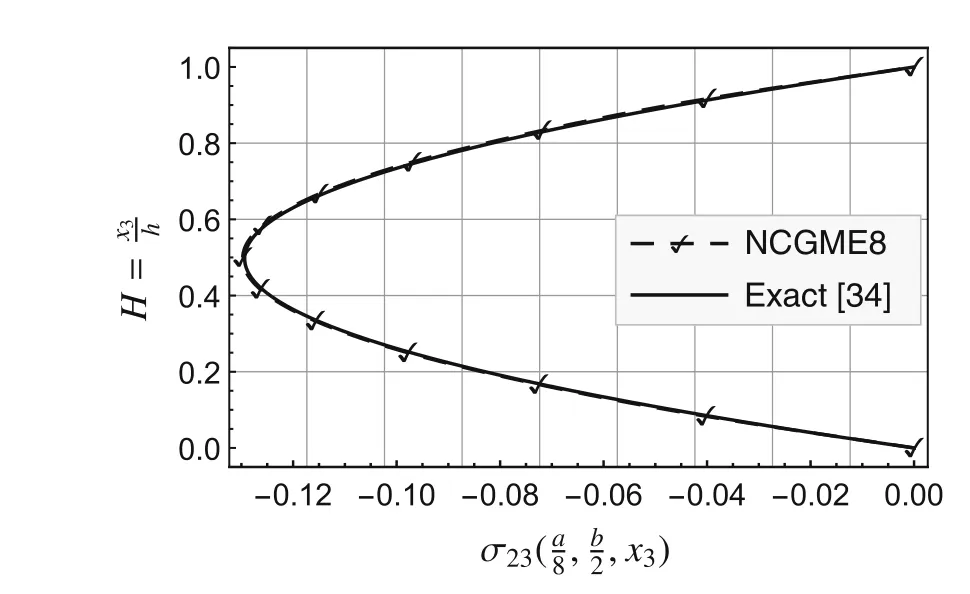
Fig.12 Distribution along thickness of

Table 1 Mesh sizes

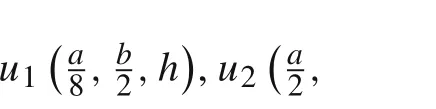
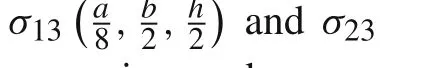
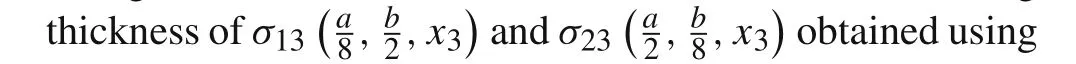
5.2 A classical cantilever beam problem

Consider a cantilever beam[35]under pure bending or acted upon by shear forces at the tip(Fig.13a,b),with geometric dimensions of2×2×10 and material properties ofE=1500 andν=0.25.The vertical displacement at point A and the bending stressσ11at point B for different meshes(as shown in Figs.14–19)are presented in Tables 2–4,respectively,compared withQ S11?1[35],Q S11?2[35],and exact solutions.

Based on the results in Tables 2–5,it can be concluded that:

Most of the displacement and stress results obtained using NCGME8 appear to be more accurate than those obtained using the hybrid stress elementsQ S11?1,Q S11?2,and CGME8.NCGME8 is less sensitive to geometric distortions(see Figs.14–19,in which the elements are severely distorted).It is also very obvious that the accuracy of CGME8 was very poor due to the geometric distortion of the elements.

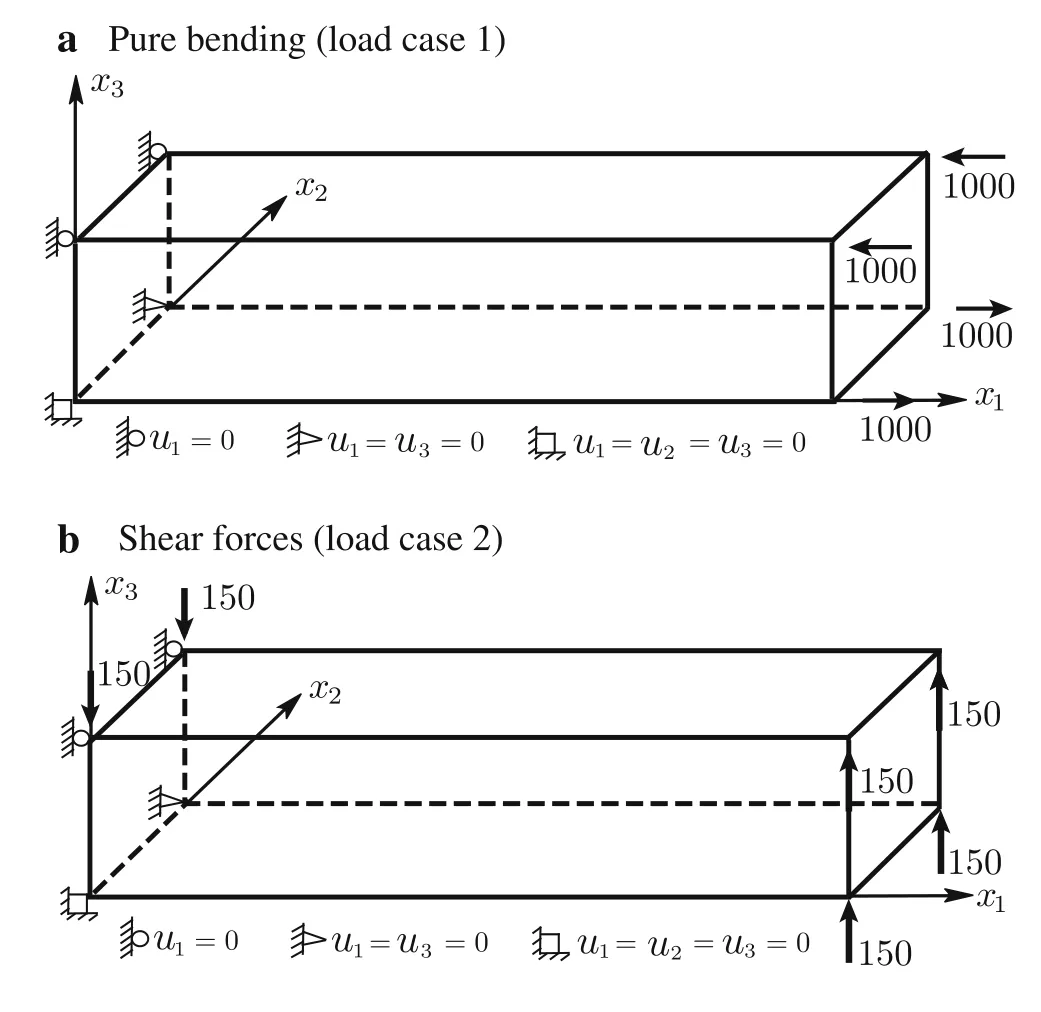
Fig.13 Two load cases for a cantilever beam

Fig.14 Mesh a

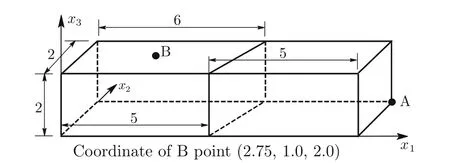
Fig.15 Mesh b

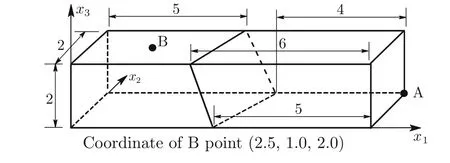
Fig.16 Mesh c

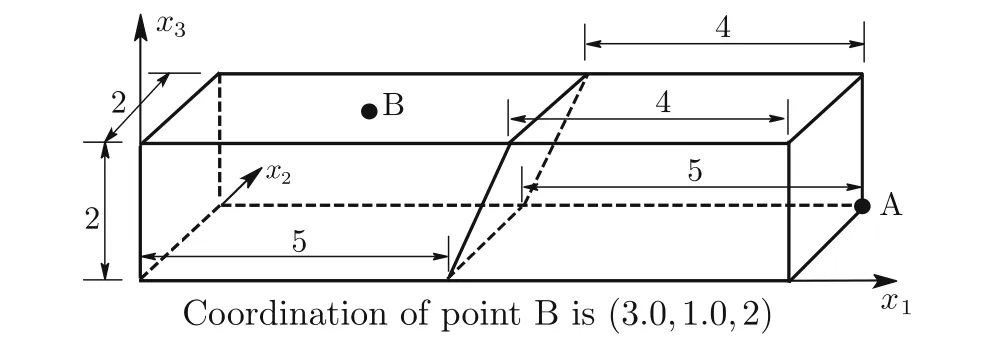
Fig.17 Mesh d

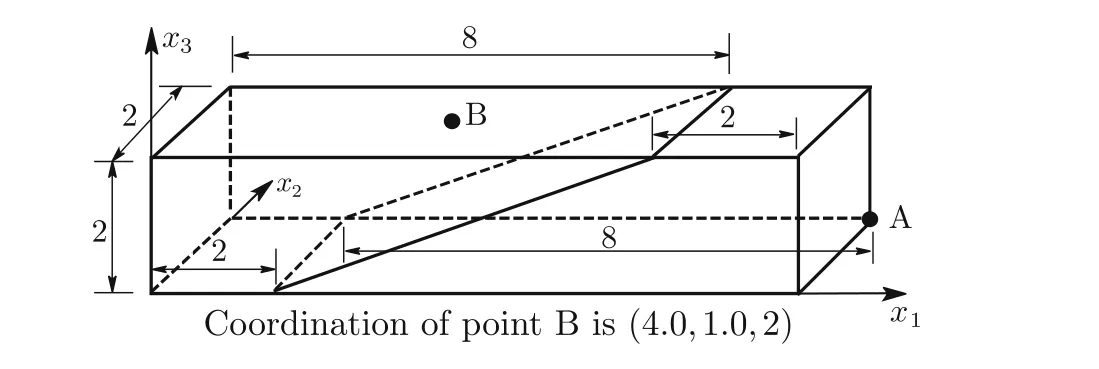
Fig.18 Mesh e

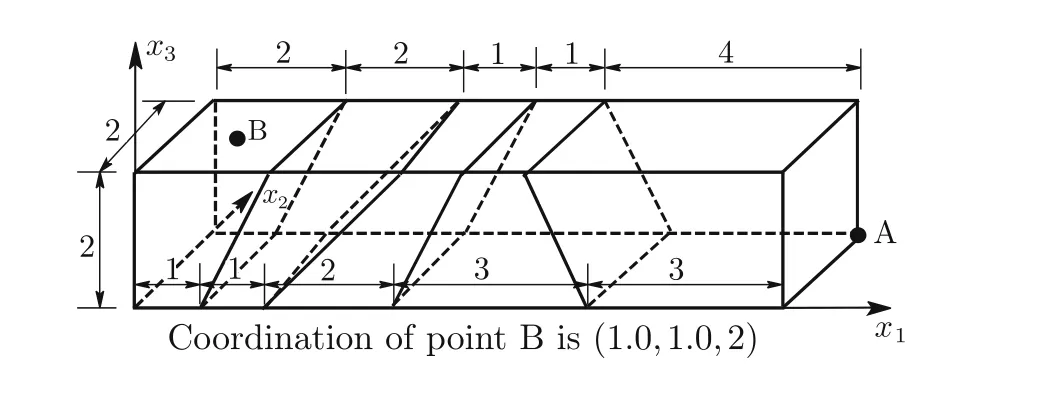
Fig.19 Mesh f

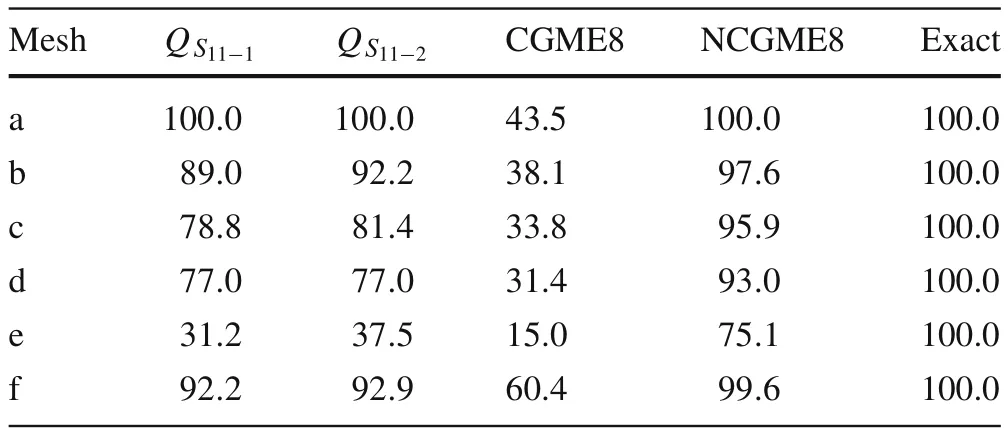
Table 2 Displacement u3 at point A(load case 1)

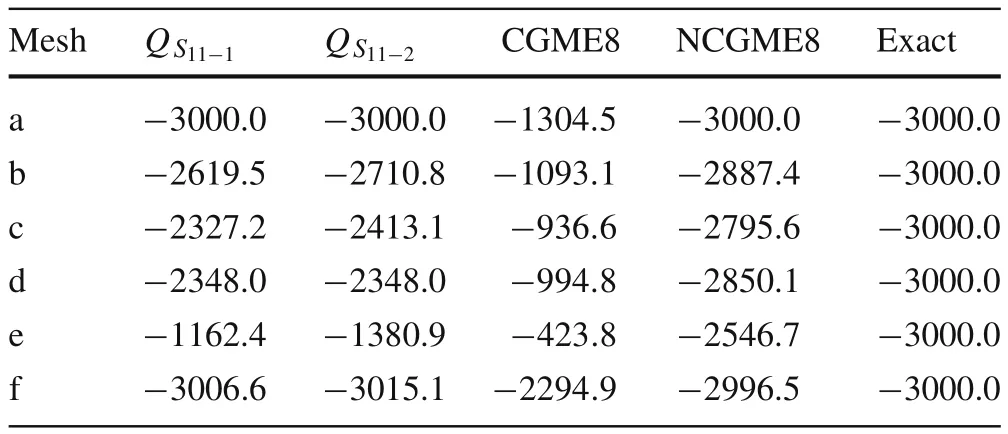
Table 3 Stress σ11 at point B(load case 1)

5.3 Cook’s skew beam

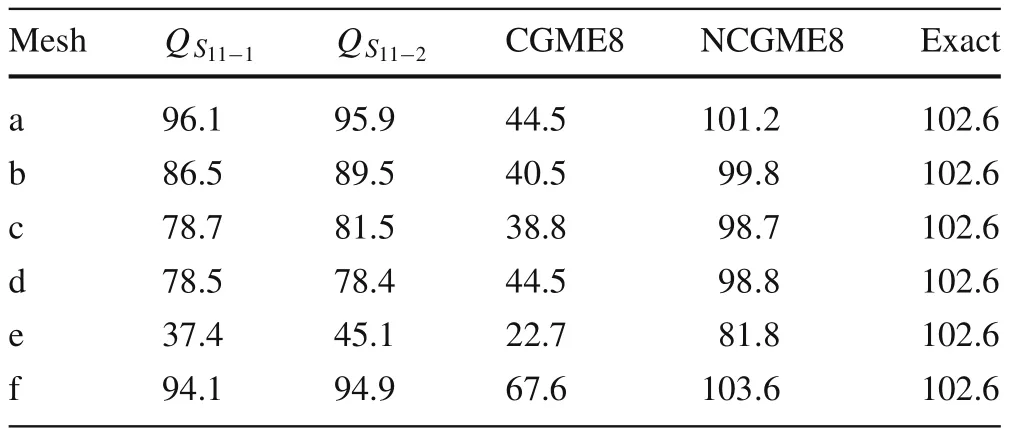
Table 4 Displacement u3 at point A(load case 2)

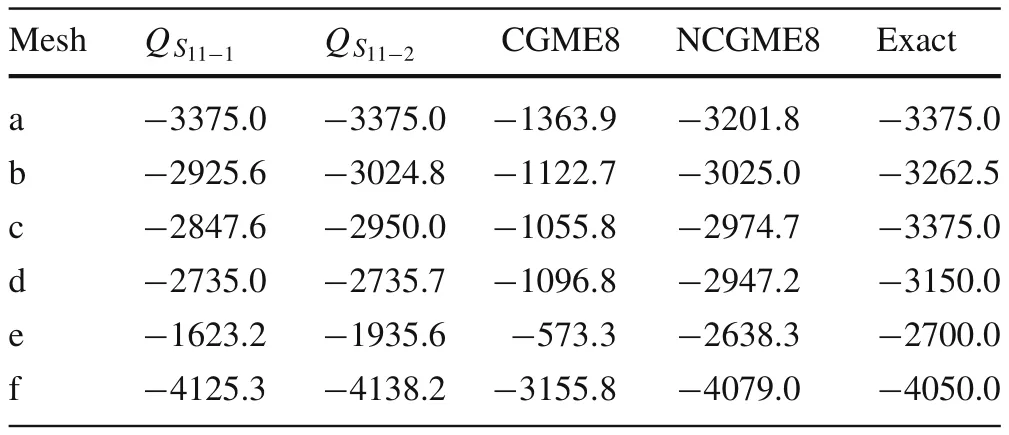
Table 5 Stress σ11 at point B(load case 2)

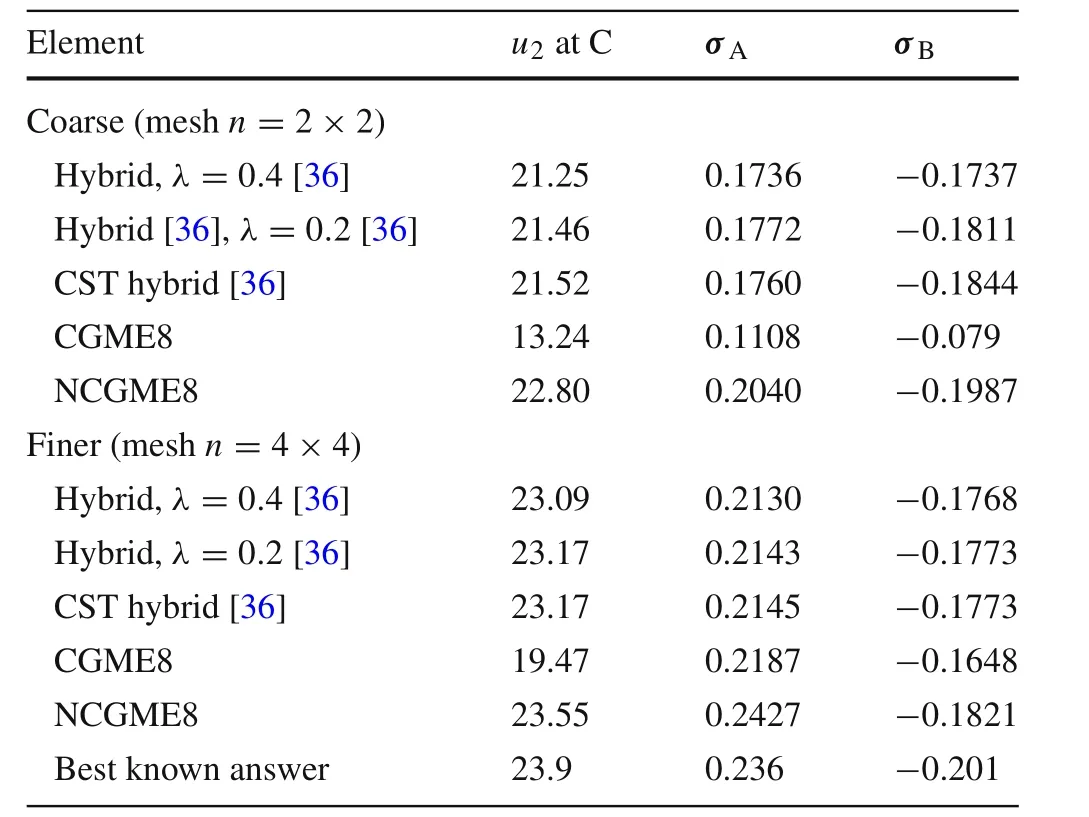
Table 6 Results for Cook’s skew beam(Fig.20)

Fig.20 Cook’s skew beam

The numerical results in Table 6 show that NCGME8 was softer than the other elements in Ref.[36].Without doubt,the results obtained using NCGME8 are closer to the best known answers.

6 Conclusions

Generally,classical mixed methods yield the simplest and most flexible system of equations for finite element analysis of some problems.However,the corresponding mathematical theory is relatively complex due to the requirement for stable elements.

Applying usual linear interpolation functions,two novel and simple generalized mixed elements were developed by combining two variational principles.As mentioned in Sect.3,one of the most prominent advantages of the generalized mixed methods(GMMs)corresponding to the present mixed elements for the 3D problems presented in this work is that symmetry with respect to both displacement and stress variables is guaranteed in the finite element governing equations.On the other hand,the GMMs are preferable for introduction of displacement and tractions boundary conditions simultaneously.The convergence rates of stress and displacement variables using NCGME8 were balanced,stable,and with fine precision.

This noncompatible generalized mixed method should be extended to important applications in a wide range of engineering structures,including treatment of the combination with other structural members and investigation of the possible advantages in stress singularity problems and nonlinear applications which may result for special structures.The pertinent theories of the generalized mixed elements should also be explored deeply,for instance,investigation of local error bounds or practical estimates for variables in threedimensional problems.

If one starts from the generalized variational principles of plate and shell theories,simple corresponding generalized element formulations and generalized mixed methods can also be constructed.

AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grant 11502286).

1.Tian,S.Z.,Pian,T.H.:Variational Principles with Multi-variables and Finite Elements with Multi-variables.Science Press,Beijing(2011).(in Chinese)

2.Hoa,S.V.,Wei,F.:Hybrid Finite Element Method for Stress Analysis of Laminated Composites.Springer Science&Business Media,New York(2013)

3.Herrmann,L.R.:Finite element bending analysis for plates.J.Eng.Mech.Div.ASCE 98,13–26(1967)

4.Brezzi,F.:On the existence,uniqueness and approximation of saddle-point problems arising from lagrangian multipliers.Rev.Fr.Autom.Inf.Rech.Opér.Anal.Numér.8,129–151(1974)

5.Reddy,J.N.,Oden,J.T.:Mathematical theory of mixed finite element approximations.Quart.Appl.Math 33,255–280(1975)

6.Oden,J.T.,Reddy,J.N.:On mixed finite element approximations.SIAM J.Numer.Anal.13,393–404(1976)

7.Strang,G.,Fix,G.J.:An Analysis of the Finite Element Method.Prentice-Hall,Englewood Cliffs(1973)

8.Atluri,S.N.,Gallagher,R.H.,Zienkiewicz,O.C.:Hybrid and Mixed Finite Element Methods.Wiley,New York(1983)

9.Hughes,T.J.:The Finite Element Method:Linear Static and Dynamic Finite Element Analysis.Courier Corporation,North Chelmsford(2012)

10.Morley,M.E.:A family of mixed finite elements for linear elasticity.Numer.Math.55,633–666(1989)

11.Brezzi,F.,Fortin,M.:Mixed and Hybrid Finite Element Methods.Springer Science&Business Media,New York(2012)

12.Belytschko,T.,Liu,W.K.,Moran,B.,et al.:Nonlinear Finite Elements for Continua and Structures.Wiley,New York(2013)

13.Bonet,J.,Wood,R.D.:Nonlinear Continuum Mechanics for Finite Element Analysis.Cambridge University Press,London(1997)

14.Zienkiewicz,O.C.,Taylor,R.L.:The Finite Element Method:Solid Mechanics.Butterworth,London(2000)

15.Arnold,D.N.:Differential complexes and numerical stability.Preprint.arXiv:math/0212391(2002)

16.Arnold,D.N.,Winther,R.:Mixed finite elements for elasticity.Numer.Math.92,401–419(2002)

17.Adams,S.,Cockburn,B.:A mixed finite element method for elasticity in three dimensions.J.Sci.Comput.25,515–521(2005)

18.Arnold,D.N.,Falk,R.,Winther,R.:Mixed finite element methods for linear elasticity with weakly imposed symmetry.Math.Comput.76,1699–1723(2007)

19.Arnold,D.N.,Awanou,G.,Winther,R.:Finite elements for symmetric tensors in three dimensions.Math.Comput.77,1229–1251(2008)

20.Sinwel,A.:A new family of mixed finite elements for elasticity.[Ph.D.Thesis],Johannes Kepler University,Austria(2009)

21.Qiu,W.,Demkowicz,L.:Variable order mixedh-finite element method for linear elasticity with weakly imposed symmetry.II.Affine and curvilinear elements in 2D.Mathematics 11,510–539(2010)

22.Gopalakrishnan,J.,Guzm,J.N.:Symmetric nonconforming mixed finite elements for linear elasticity.SIAM J.Numer.Anal.49,1504–1520(2011)

23.Qiu,W.:Mixed variable orderh-finite element method for linear elasticity with weakly imposed symmetry.Curvilinear elements in 2D.Comput.Methods Appl.Math.11,510–539(2011)

24.Hu,J.,Man,H.G.,Zhang,S.G.:The simplest mixed finite element method for linear elasticity in the symmetric formulation onnrectangular grids.Comput.Math.Appl.71,1317–1336(2013)

25.Liu,Z.D.:Basis of Mixed Finite Element Methods and Its Application.Science Press,Beijing(2006).(in Chinese)

26.Arnold,D.N.:Mixed finite element methods for elliptic problems.Comput.Methods Appl.Mech.Eng.82,281–300(1990)

27.Reissner,E.:On a variational theorem in elasticity.J.Math.Phys.29,90–95(1950)

28.Chien,W.Z.:Method of high-order lagrange multiplier and generalized variational principles of elasticity with more general forms of functionals.Appl.Math.Mech.4,143–157(1983)

29.Felippa,C.A.:Parameterized multifid variational principles in elasticity:I.Mixed functionals.Commun.Appl.Numer.Methods 5,79–88(1989)

30.Felippa,C.A.:Parametrized multifid variational principles in elasticity:II.Hybrid functionals and the free formulation.Commun.Appl.Numer.Methods 5,89–98(1989)

31.Zhong,W.X.:Force,Work,Energy and Symplectic Mathematics.Dalian University of Technology Press,Dalian(2007).(in Chinese)

32.Chen,W.J.:A high preccision eight-node hexahedron element.Chin.J.Theor.Appl.Mech.10,1211–1219(1976)

33.Taylor,R.L.,Beresford,P.J.,Wilson,E.L.:A non-conforming element for stress analysis.Int.J.Numer.Methods Eng.10,1211–1219(1976)

34.Fan,J.R.:Exact Theory of Laminated Thick Plates and Shells.Science Press,Beijing(1996).(in Chinese)

35.Cheung,Y.K.,Chen,W.J.:Isoparametric hybrid hexahedral elements for 3-D stress analysis.Int.J.Numer.Methods Eng.26,677–693(1988)

36.Cook,R.D.:A plane hybrid element with rotational DOF and adjustable stiffness.Int.J.Numer.Methods Eng.24,1499–1508(1987)