Mengjiao Zhang, Weiqiang Tan, Junhui Gao, Shi Jin,＊

1 National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China.

2 School of Computer Science and Educational Software, Guangzhou University, Guangzhou, 510006, China.

* The corresponding author, email: jinshi@seu.edu.cn

I. INTRODUCTION

Since scarce spectrum and large consumption of power have been the essential factors that restrict the development of communication technology, massive multi-input multi-output(MIMO) technology is born to improve spectral efficiency (SE) without sacrificing other communication resources. Massive MIMO, in which the base station (BS) is equipped with very large antenna arrays and simultaneously serves tens of users in the same time-frequency resource, can utilize the freedom of space efficiently and reduce transmit power for the uplink [1] and downlink [2,3]. To achieve MIMO gains, cooperation scheme among BS is very essential and a method based on rateless network coding is proposed without perfect synchronization [4]. In addition, a recent research has investigated the SE of MIMO transmission systems with hybrid architectures based on discrete Fourier transform processing [5]. The achievable SE of millimeter wave MIMO downlink cellular systems is derived when the BS employs a uniform linear array and maximal ratio transmission [6]. Massive MIMO is an important incubator for future energy-efficient and spectrum-efficient broadband networks development [7]. As a result,it’s rather essential to build a Massive MIMO prototype system to promote the development of this technology. The authors in [8] presents a time division duplex (TDD)-based 128-antenna massive MIMO prototype system from theory to reality.

So far, a considerable proportion of literature propose some models based on ideal hardware, but actually the hardware cost and energy consumption scales linearly with the number of antennas and thus can become intolerable. Huge hardware cost and power consumption of digital processing units related to antennas is becoming a bottleneck problem in receiver design. It can be more cumbersome and tricky to design the receiving part of signal in wireless communication systems and the power consumption at the receiver is the main source of whole system’s power consumption. If we take the uplink receiver in a massive MIMO system as an example,the energy consumption is greatly effected by the number of quantization bits. ADC’s power loss increases linearly with the sampling rate and exponentially with the number of bits per sample [9]. As a result, low precision ADC is adopted widely. The authors of [10] developed a framework for studying the best possible estimation performance of the quantized MIMO system by adopting a joint channel-and-data estimation method based on Bayes-optimal inference. However, considerable rate loss and channel estimation challenge are problems that can not be ignored. In order to get a balance between system performance and power consumption, the authors in [11] proposed a mixed-ADC architecture initially, using a fraction of full-resolution ADCs to enhance the system performance and low-resolution ADCs to take power consumption into account. One typical retard in ADC analysis is that relevant computation about predictive quantizer can be dif ficult due to the nonlinear nature of scalar quantizer. According to [12], a classical approach was proposed to handle nonlinearity, where the quantizer is approximated as a line gain with additive Gaussian white noise(AWGN). This model ignores the internal characteristics of the ADCs, and therefore the calculation is simple and convenient. Since previous studies have shown that this type of approximation has well performance, this paper adopts the additive quantization noise model (AQNM) to analyze the quantization problem [13].

This paper investigates the achievable uplink spectral eきciency (SE)of a massive multi-input multi-output(MIMO) system with a mixed analog-to-digital converter (ADC)receiver architecture,in which some antennas are equipped with full-resolution ADCs while others are deployed with low-resolution ADCs.

Most of the literature on massive MIMO assume a conventional architecture built on ideal hardware and the research on mixed-ADC architecture is not suf ficient. The authors of [14] examined the uplink achievable rate for massive MIMO systems under Rayleigh fading channel with low-resolution ADC and maximum ratio combining (MRC) detector.Based on the research result, the authors of[15] obtained the achievable SE of single-cell massive MIMO system with mixed-ADCs and presented the theoretical and approximate expression of the achievable. However, relevant literature that discuss in more general system environment setting, such as Rician fading channel, remain vacant now. The authors of[16] examined the achievable SE of single-cell massive MIMO system with low resolution ADCs and zero-forcing (ZF) detector.

This paper shall go deep into the analysis on massive MIMO system to fill some vacancy based on existing research result. First, the system environment is set in multi-cell system with Rician fading channel. Actually, there have been some research focusing on issues on secure communication and relay network in multi-cell systems [17–20]. The work in [17]investigated the secrecy performance of the target MISO SWIPT system with imperfect channel state information. In [18], the authors adopted a secure switch-and-stay combining protocol for cognitive relay networks. In this work, we investigate the achievable SE of system and deriving approximate expressions of achievable SE under MRC detector. Based on the derived theoretical analysis, the effect of some important insight, including the number of BS antennas, the user transmit power, the number of quantization bits of the low-resolution ADCs, and the proportion of full-resolution ADCs in the mixed structure on the achievable SE is revealed.

As a result, massive MIMO system with mixed-ADC architecture can achieve a considerable proportion of the channel capacity at a relatively small price [21]. To maximum the achievable SE, how to allocate transmit power among users is necessary to discuss.Traditional equal power allocation algorithm can not take advantage of the fading of the wireless channel [1] and an iterative algorithm was previous proposed to optimize transmit power matrix and uplink reception matrix. After learning from previous research, the paper proposes two power allocation algorithms for multi-cell mixed-ADC massive MIMO systems, which reduce computational complexity.As expected, our results showcase that proposed power allocation algorithms have superiority over equal power allocation algorithm and remarkably improve the total achievable SE. With the ZF detector, the theoretical and approximated expression is also derived in multi-cell system under Rayleigh fading channel. Analysis and simulation results showcase that the achievable SE can be improved by increasing of transmit power, the number of antennas, the proportion of full-resolution ADCs and quantization precision of the low-resolution ADCs.

The remaining part of this paper is organized as follows. Section II outlines the system model. Section III derives a closed-form approximation of the achievable SE of massive MIMO system with MRC detector under Rician fading channel and gives a specific analysis of the effects of some key parameters on the achievable SE. Section III presents power allocation algorithms of multi-cell mixed-ADC massive MIMO systems based on the the lower and upper bound of the approximate achievable SE. Section IV discusses the achievable SE of the single-cell system under Rayleigh fading channel with ZF detector and analyzes the in fluencing factor of the achievable SE. Numerical results are presented in Section V to corroborate the analysis. Finally,section VI gives a conclusion of the paper.

Notations—Throughout the paper, vectors and matrices, such as x and X, respectively,are denoted in bold typeface, while scalars are presented in normal typeface, such as x. Moreover, (?)Tdenotes the transpose of a matrix,while ‖?‖ andrepresent the Euclidean norm and the absolute value, respectively.Also, tr(?) and E{?} represent the trace and expectation operators, respectively, IMdenotes an M ×M identity matrix. CN(μ,σ2)denotes a complex Gaussian distribution with mean μ and variance σ2.

II. SYSTEM MODEL

We consider multi-user uplink massive MIMO system with N single-antenna users and M receiver antennas (M ? N) at the BS. A mixed-ADC architecture includes M1full resolution ADCs and the remaining M2(M2=M?M1)ADCs have low-resolution. The proportion of full-precision ADCs is represented by κ,which means κ=M1/M . (0≤κ≤1). Consider a multi-cell multi-user uplink massive MIMO system with Rician fading channel.There are w interference cells around the target cell. For the sake of simplicity, all expressions of analysis are based on the target cell w=0.

In order to have a brief understanding of the transmit model, the received signal at the BS before quantization is denoted simply by

where xw∈?N×1denotes transmit signal vector for w-th cell. Λwis the diagonal matrix,i.e. ,

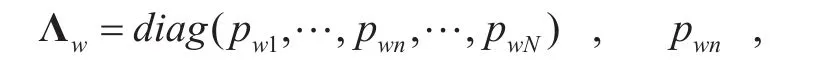
whose entries are used to signify the transmit power of each user. n～CN(0,1) is the AWGN in the channel and Gw∈?M×Nis the channel matrix from the BS to the users. The channel matrix consists of large scale fading and fast fading, which is modeled as

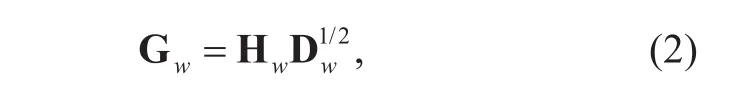
where Dwdenotes the large scale fading whose diagonal element is the large scale fading coefficient of each user in w-th cell,which is presented by expression [D]nn=βn.The fast fading matrix Hwwhich refers to the de finition in [22] embodies two parts, namely a deterministic component corresponding to the LOS signal and a Rayleigh-distributed random component which accounts for the scattered signals. The ratio of the power of the deterministic component to the power of the scattered components is represents by Rician factor κ. According to the de finition of Rician fading channel in [23], the fast fading matrix can be written as

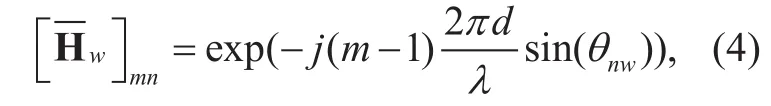
where d denotes the inter-antenna spacing,λ represents the wavelength of the carrier, and θnwdenotes the arrival angle of n-user’s direct path in the cell. For the convenience of calculation, we assume that the inter-antenna spacing equals to d=λ/2.

For a mixed-ADC architecture, the channel matrix is split to two parts according to the property of ADCs as follows

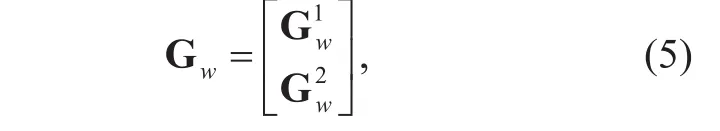
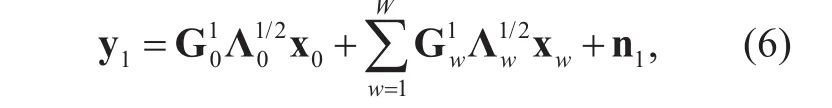
where n1～CN(0,1) is the AWGN in the channel.

For low-precision ADCs structure, the quantization bit of utilized nonlinear scalar quantizer of low resolution ADCs is set as b.We adopt AQNM [25] since previous studies have shown that this type of approximation has well performance [13], [26]. The quantizer can be described as a linear gain, along with additive noise uncorrelated with the quantizer input [13], then the received signal of the low-precision ADC can be approximated as

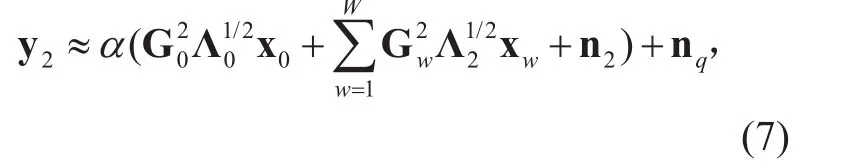
where nqis the additive Gaussian quantization noise vector that is uncorrelated with the input of quantizer. Let α=1?ρ, ρ is the inverse of the signal-to-quantization-noise ratio.Assuming that the input signal via the quantizer is Gaussian and non-uniform scalar minimum mean-square-error quantizer is utilized,the values of ρ are listed in Table I for b≤5 and can be approximated by [14]. Considering the limiting condition, when b→∞, we have α→1.

Synthesizing two types of signals, we can get detailed receiver signals in multi-cell system

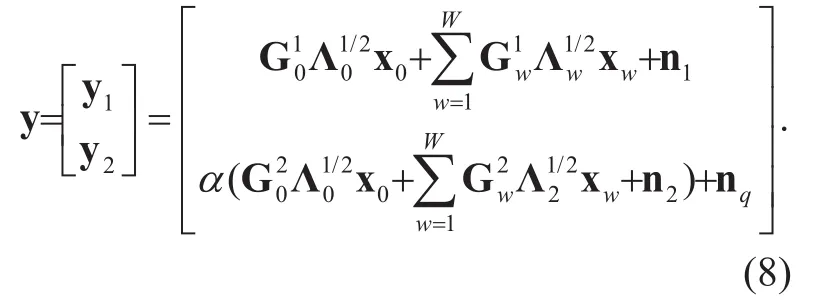
Without loss of generality, we assume that each cell can obtain their own real-time CSI and interference cell’s long-time CSI, including the arrival angle of LOS path θwn, transmit power matrix Λw, large scale fading coef-ficient βwn, and Rician fading factor Kwn. The signal after the channel detection of receiver is as follows:

Table I. ρ for different ADCs quantization bit (b ≤ 5).

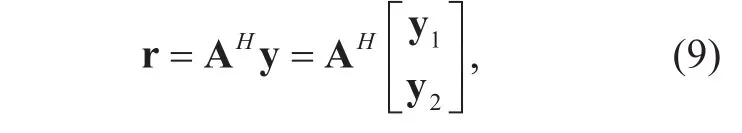
where A is the reception matrix of linear detector, such as MRC detector and ZF detector.(9) can be further expressed as

where A=[A1; A2], among which A1∈?M1×Nwhile A2∈?M2×N. With a combination of(8) and (9), the expression of the signal after channel detection in multi-cell massive MIMO system is derived. Then the n-th element of r can be expressed as

where anis the n-th column of reception matrix A, an1includes the first M1elements while an2includes the last M2elements. gwiis the i-th column of Gw,includes the first M1elements whileincludes the last M2element of gwi.pwiis the speci fied power for i-th user in w-th cell, and xwiindicates the transmit data of i-th user in w-th cell.Then, we can get the preliminary expression of received signal and the model of single-cell multi-user uplink massive MIMO system system is set up.

III. ANALYSIS OF MULTI-CELL SYSTEM WITH MRC DETECTOR

In this section, we calculate the theoretical expression and its closed-form approximation of achievable SE of massive MIMO system with Rician fading channel. Based on the approximate expression, we figure out what impacts some key parameters can have on the achievable SE, including the number of BS antennas, the user transmit power, the number of quantization bits of the low-resolution ADCs, and the proportion of full-resolution ADCs in the mixed structure. Furthermore, we present power allocation algorithms of multicell mixed-ADC massive MIMO systems based on the the lower and upper bound of the approximate achievable SE.

3.1 Achievable SE analysis

MRC linear detector has significantly lower computational complexity than other linear detectors such as the zero-forcing and linear minimum mean square error estimators. In massive MIMO system, very high spectral efficiency can be obtained even with simple MRC processing at the same time as the transmit power can be cut back by orders of magnitude and that this holds true even when taking into account the losses associated with acquiring CSI from uplink pilots [1]. First, it’s necessary to emphasize that all analysis and symbols here in multi-cell system are around the target cell (w=0) and thus, with MRC detector, we can have

and

According to the assumption in [27], we think the interference signal and noise are AWGNs which is uncorrelated with the target signal. Then, the expression of achievable SE is written as (14) shown in the bottom at this page.

It is worth noting that the operation of expectation calculation is for the fast fading factor of the channel and each sample is a concrete realization of the channel. If rigorous analysis on achievable SE is required, we need to analyze the probability density function of the fractional term in the logarithmic function.But, the expression is too complicated to calculate, hence a more stringent approximate expression is necessary for the actual application. An approximate expression of (14) is given in Theorem 1.

Theorem 1. For the uplink of single-cell mixed-ADC massive MIMO systems with ZF detector, under perfect CSI, the achievable SE of the n-th user can be approximated as (16)shown in the bottom at this page.

Proof: To derive theoretical result of the achievable SE, we seek for the approximated result in [20] which is exactly suitable for massive MIMO system. When the number of antennas M is finite but very large, this approximated can be quite efficient. The progressive expression holds as follows

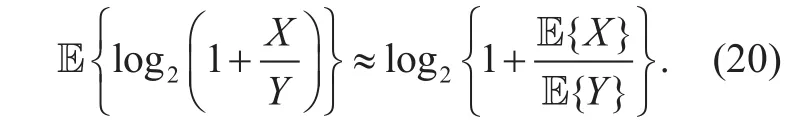
The prerequisites of using this formula is that X and Y are independent and converge to respective mean as M→∞. Then, the achievable SE can be approximated as (21) shown in the bottom at this page.

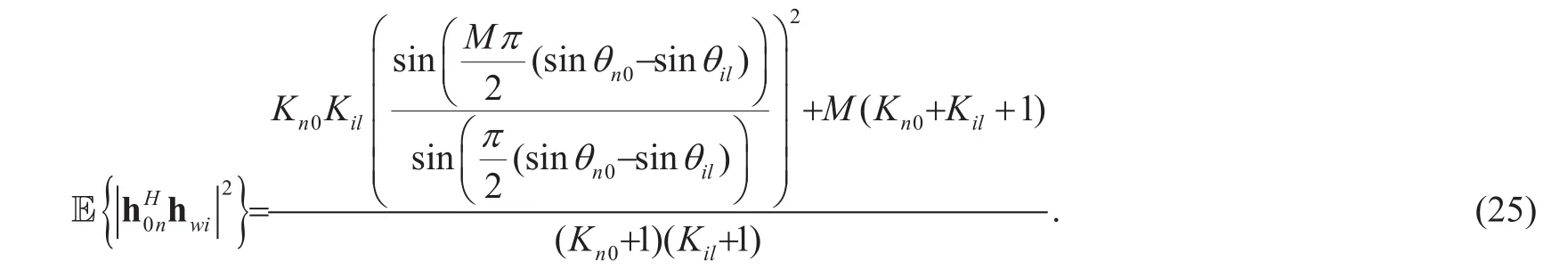
The denominator of (21) contains four sources of noise from the interference signal of the same cell, the interference signal of the surrounding cell, the channel noise, and quantization error. Now the problem is converted into calculating each expectation term in (21).Before we commence calculation, we need some preliminary work [22]. Recall the de finition of the fast fading expression in (3) and (4)and we can figure out

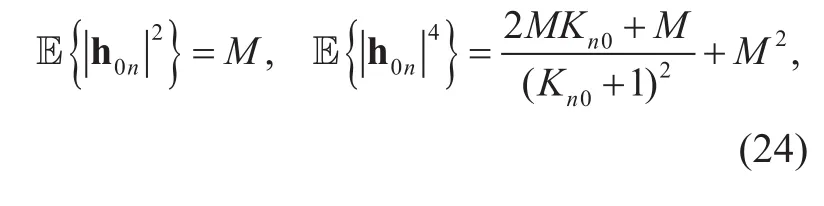
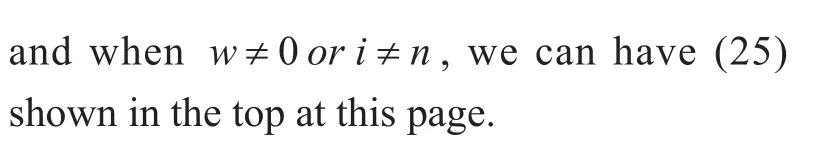
Substituting (24) and (25) into (21), then we can obtain the expectation of the interference signal of the same cell σ1, the expectation of the interference signal of the surrounding cell σ2, the expectation of channel noise. The final expressions of the three parts are shown in the first term of denominator of (16),Ξ1, and the last term of denominator of (16), respectively. The only left term to calculate is expectation of the quantization noise and the key step is to get the covariance matrix of nqfor a fixed channel realization. Using the similar method to the previous subsection,can be given approximately as

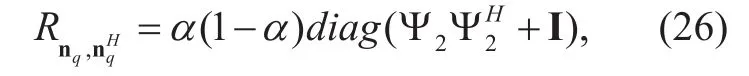
where

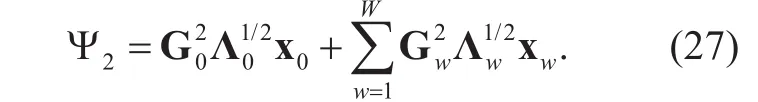
Substituting (26), (24), and (25) intowe obtain the desired result Ξ2. Finally, Theorem 1 is veri fied.

Next, let’s consider some special cases.

1) Assume that there is no LoS component that means the Rician channel reduces to Rayleigh channel, which leads tothe expression of achievable SE degrades to

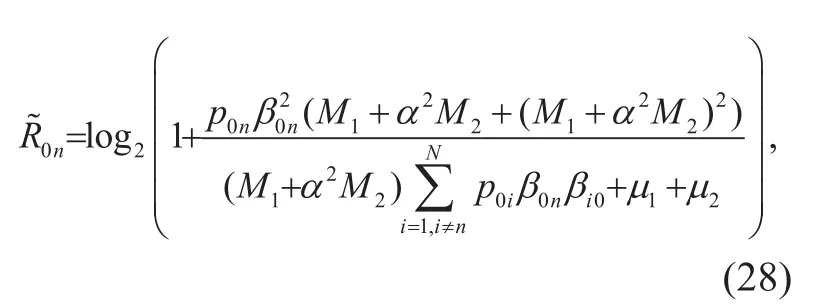
where

and

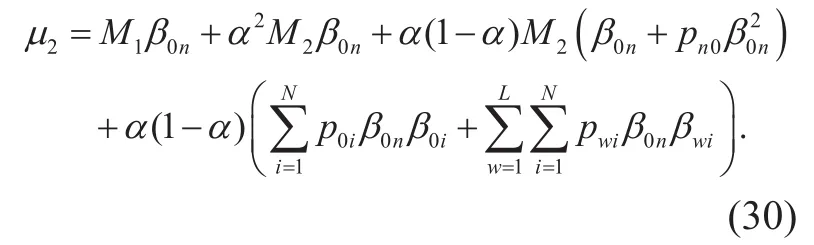
When the interference cell is not considered and the power allocation for each user of each cell is assumed to be equal, the achievable SE expression is further degraded to

where

It is obvious that the achievable SE is a function of the the number of full-resolution ADCs, the number of low-resolution and ADCs, the user transmit power, and the number of quantization bits. We observe that this result is consistent with conclusion in [15]about the achievable SE of single cell MIMO system with Rayleigh fading channel

3.2 Power allocation analysis

The expression of the achievable SE is a function of the transmit power, but it can not be enhanced by increasing the transmit power for the reason that the transmit power has a positive impact on both the target signal and interference signal. The following study is to find a optimized power allocation algorithm to maximize the total achievable SE of the target cellEach user’s transmit power need to meet total power upper bound, i.e.,and minimum transmit power constraint, i.e.,p0n＞. Since above discuss has provedhas a considerable approximation to R0nand in order to simplify calculation, we replace R0nwithto participate in the analysis on power allocation. For convenience, we recordas below.

where μ1is as follows according to (16)

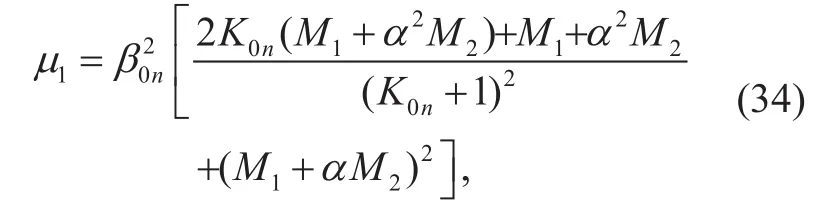
and

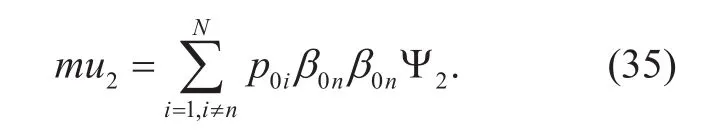
Naturally, μ3is the rest part of the denominator of (16) and the speci fic expression will not be repeated here. Among which, p0nneeds to satisfy the power constraint and we can have

The values besides the inequations imply the two extreme cases of the interference from users within a single cell. The lower bound 0 means that all power is consumed by n-th user and there is no interference from other users. The upper bound μ2max indicates that each user transmit signals as total maximum transmit power.is used to represent the lower bound on the achievable SE whiledenotes the upper bound on the achievable SE.Since μ2appears in the denominator, then the upper bound of δ2corresponds towhile the lower bound of δ2corresponds to.Thus, we have

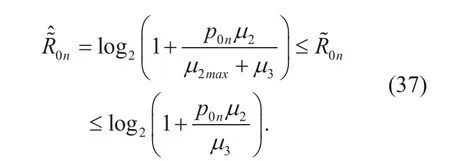
We adopt water-pouring algorithm to allocate transmit power between users. Water-pouring algorithm (also known as annotation algorithm) is based on channel circumstances, where the channel with a large signalto-noise ratio gets more power while the channel with a small signal-to-noise ratio gets less power, to optimize overall performance of the whole cell. Based on the proposed lower bound and upper bound of the achievable SE,the power allocation algorithms in both cases are discussed below according to [28].

For the special case of the lower limit, the goal is to maximize. Allocated transmit power satis fies

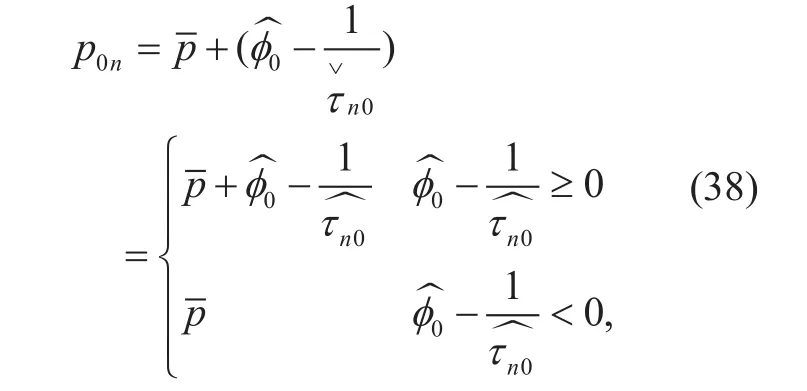
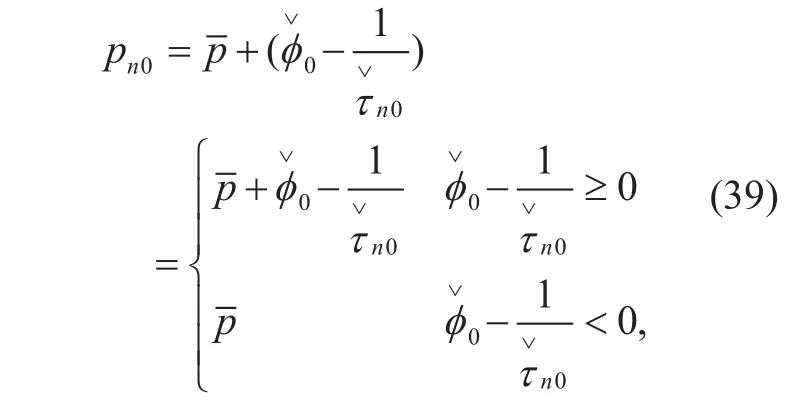
Synthesizing the result of (38) and (39),we can find that this scheme is in line with the avarice of water-pouring algorithm. When the channel has a high SNR, the system tend to allocated more power for it, which is greedy but efficient. Moreover, when the number of BS antenna M→∞,which implies that the proposed two allocation algorithms will be extremely close to equal power allocation algorithm when M becomes large enough.

IV. ACHIEVABLE SE OF SYSTEM WITH ZF DETECTOR

Since MRC detector has a low computational complexity and brings the loss of a proportion of system performance and inter-user interference. This section focus on ZF detector on massive MIMO system and seek some improvements in system performance. The advantage is that ZF detector can remove inter-user interference and brings no estimation-error. Consider the complexity of the approximate expression of the achievable SE,here we just discuss the achievable SE of the single-cell system with Rayleigh fading channel. Let Kiw=0 and w=0 in (14), then we get the theoretical expression of the achievable SE

where

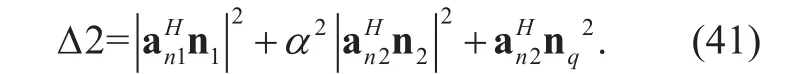
According to the working principle of ZF detector [27–29], the reception matrix can be written as follows

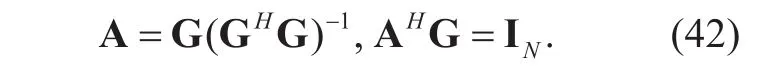
Based on this definition, the result of the achievable SE is shown in Theorem 2.

Theorem 2. For the uplink of single-cell mixed-ADC massive MIMO systems with ZF detector, under perfect CSI, the achievable SE of the n-th user can be approximated as (43)shown in the bottom at this page.

Proof: Before the proof, recalling the approximated result in (20), the achievable SE can be approximated as (45) shown in the bottom at this page.

Therefore, the next step is to calculate each expectation term in (45) and let’s commence with the numerator. From (41), we can seewith i≠n. Since the result ofis independent of the value of m, then we can conclude that

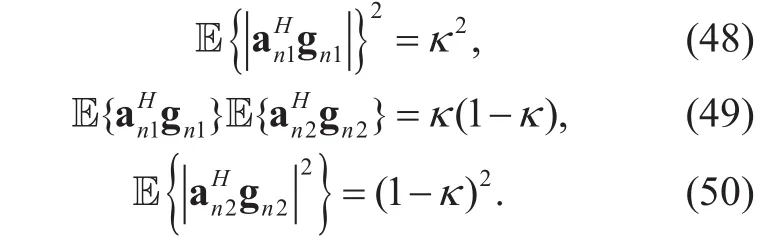
Then, the sum of three expectation terms in the numerator of (45) is (κ+α( 1?κ) )2. The next step is to calculate. First, according to the introduction about complex Wishart matrix in [32], we have

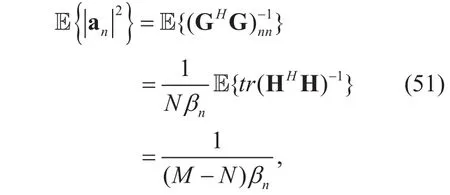
where the basis of the third equal sign is that HHH∈?N×Nhas a complex central wishart distribution with M degrees of freedom. Since the result ofis also independent of the value of m, then we can have

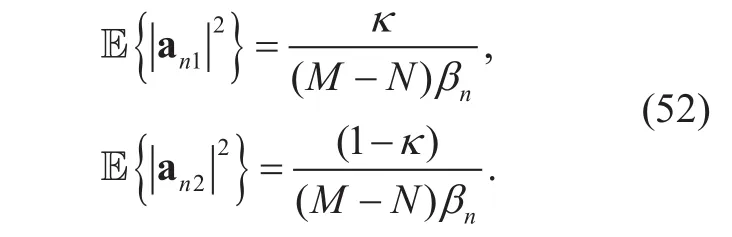
Since the independence of the reception matrix and channel noise, we can easily find

Naturally, recall the definition ofin(46) and we can have

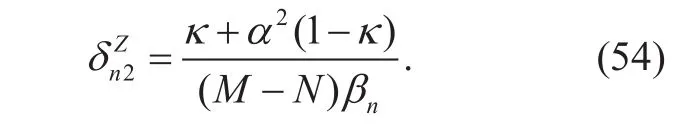
As the expression of reception matrix under ZF detector is involved with the inverse of matrix, the expression of ancan be too complicated and thus substituting it into (45) directly can be very challenging. It is of interest to find approximate solutions by simpler means than outright inversion. The channel matrix of single-cell system can be represented as follows

where D is a diagonal matrix whose diagonal element is the large scale fading coefficient of each user, which is presented by expression[D]nn=βn. With (55), we can get

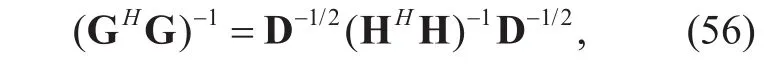
then we have

In hardware, matrix multiplication is strongly preferred over inversion since it does not require any divisions, thus we adopt the polynomial decomposition method to handel inversion in [33], which means

Substituting (58) into (57) and taking the first two terms, we can have

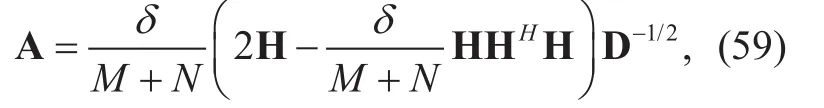
and

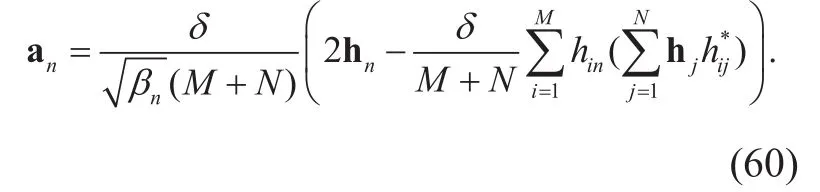
Thus, the m-th element of anis written as

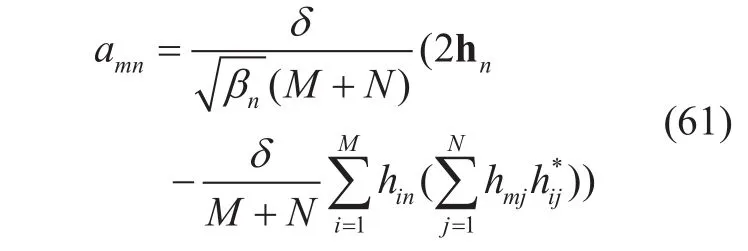
With the AQNM applied in MRC detector,the quantization noise termin ZF detector can expanded as follows

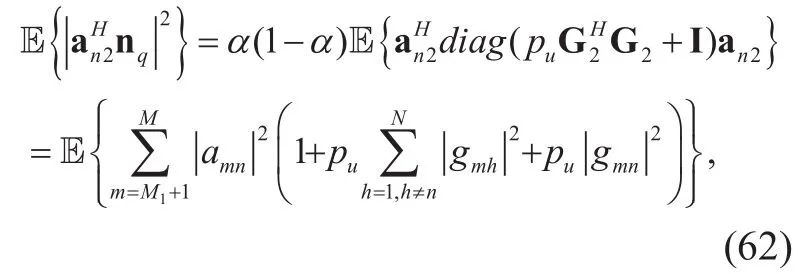
where the expression after the second equal sign consist of three expectation terms and for convenience, we let ?1beExpand ?1further,

and we get

Similarly, we have

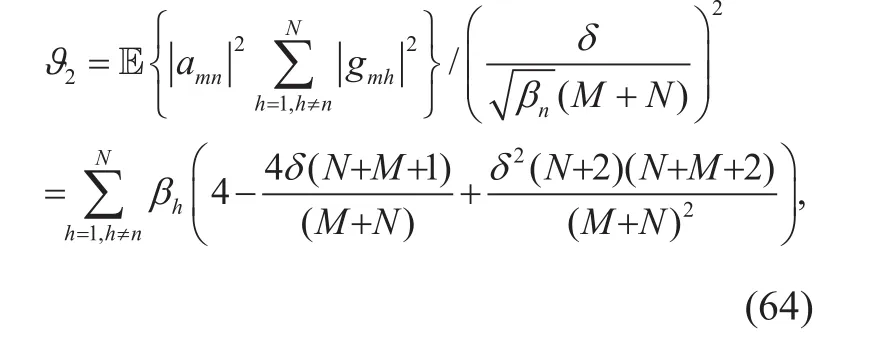
and

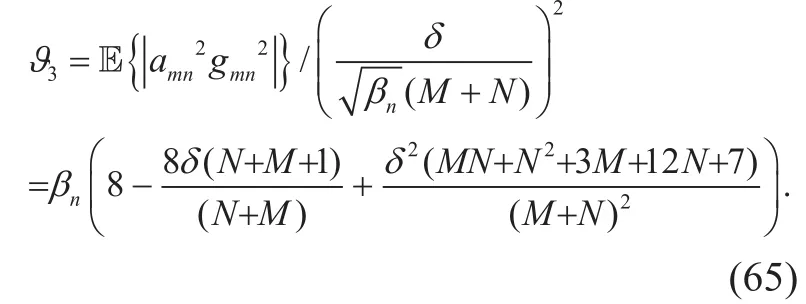
Synthesizing the definitions of ?1,?2, ?3and (62), we can get the final expression of quantization noise term as follows

Moreover, the speci fic process of calculating δnZ

1will not be repeated here and the final expression of interference noise term can be written as

Thus, Theorem 2 is veri fied. Fom Theorem 2, it can be easily found that the achievable SE is a function of the user transmit power,the number of BS antennas, the number of quantization bits and the proportion of the full resolution ADCs.

V. NUMERICAL RESULTS

Fig. 1 Total achievable SE versus the the proportion of full resolution ADCs under various b with MRC detector.

In this section we validate our previous analysis with numerical results. The achievable SE of single-cell system under MRC and ZF detector and multi-cell system is simulated separately. In simulation, we assume that each user is uniformly distributed in a hexagonal cell whose radius is set to rc=1000 m, the guard zone radius is rh=100 m. The large-scale fading coefficient is de fined as βn=zn( rn/rh)?v,the decay exponent is γ=2.1, and znrepresents the shadow-fading coefficient which is log-normal and has standard deviation σ=4.9 dB. The distance from n-th user to the BS is indicated by rnand for multi-cell system, rwndenotes the distance frm n-th user in w-th cell to the BS of the target cell. The total achievable SE of the system is de fined asAll simulation results were obtained by over 100,000 independent channel realizations.

Figure 1 shows the simulated achievable SE and its corresponding analytical approximation results versus the κ. Each sub figure depicts the achievable SE of four quantizers with different ADC bits, i.e. 1, 2, 3 and ∞ bits,and embodies two curves under κ=0.2 and κ=0.4. The achievable SE and the Rician factor K have a positive correlation, and specifically, the achievable SE increases sharply with K when 0 dB ≤K ≤20 dB, and later becomes saturated when K≥20 dB. This shows that when the channel’s Rician factor exceeds 20 dB, the impact of channel fading on achievable SE can be ignored, which means the environment is thought as strong LoS path propagation environment.

In figure 2, we depict total achievable SE versus the number of antenna under various b and K when the number of antennas is fixed at 500. From this figure, we can see the achievable SE increases with M, but growth rate decreases with the ncrease of M. The achievable SE also increases with K, but one problem in multi-cell system is that the increase of K increase the inter-cell interference and restrict the the raise of the achievable SE to some degree. We observe that there is very little advantage of increasing K, which means we can achieve a considerable proportion of the channel capacity at a relatively small price in massive MIMO system with mixed-ADC architecture.

Fig. 2. Total achievable SE versus the number of antenna under various b and K with MRC detector

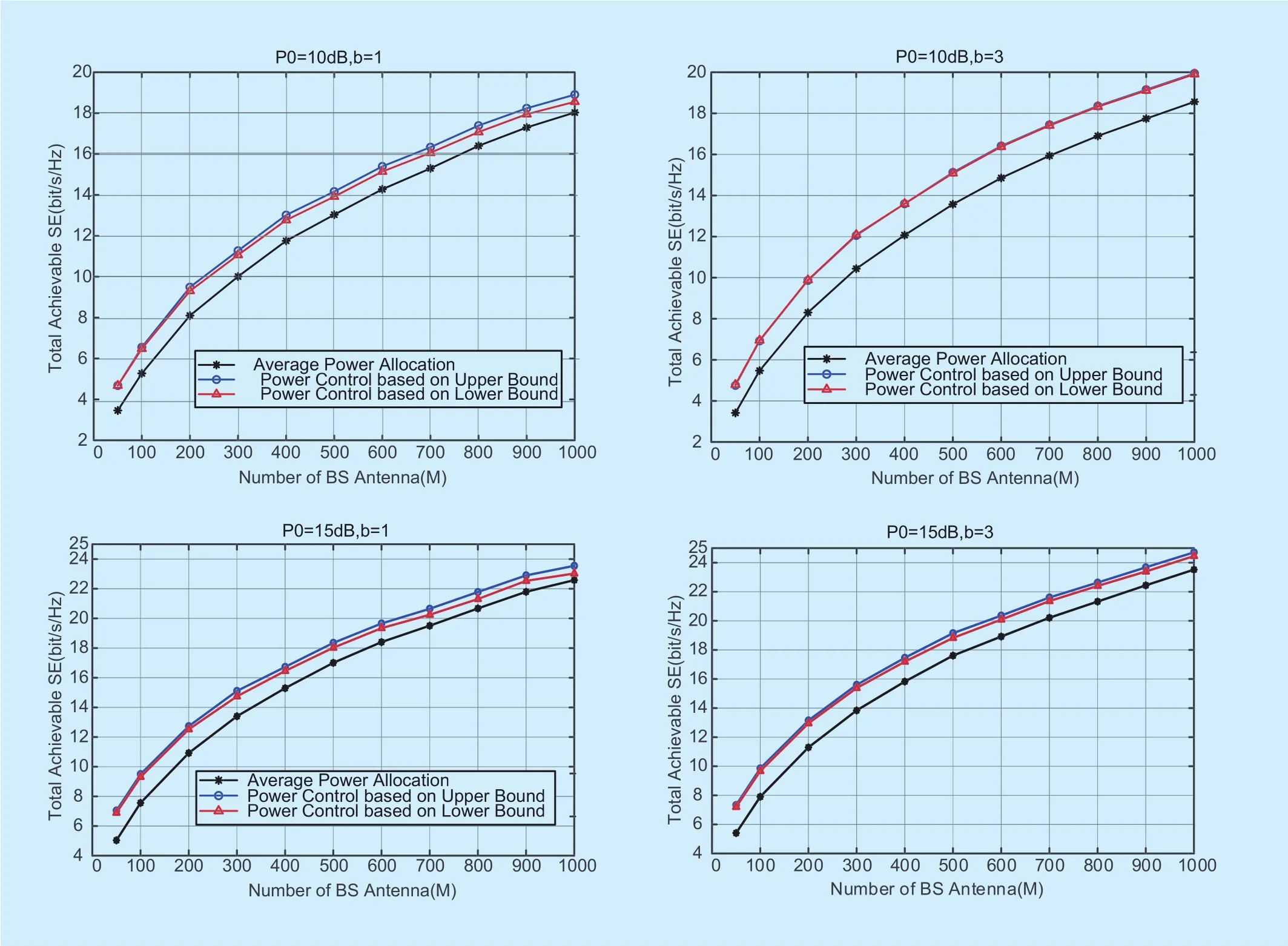
Fig. 3. Total achievable SE versus the number of antenna for three power allocation algorithms with MRC detector .

Figure 3 showcases the total achievable SE versus the number of antenna for three power allocation algorithms. Moreover, the quantization bits and transmit power are regarded as reference factor in this simulation. For convenience, Rician factor is set as 6 dB for every user. Obviously, the increase of transmit power improves the achievable SE efficiently and this improvement gets more obvious as M increases, which is consistent with our analysis result. When in low SNR regime,such as pu=10 dB, two proposed power allocation algorithms perform almost the same and both better than equal power allocation algorithms. But under high SNR regime, such as pu=15 dB, the gap between the algorithm based on the upper bound and algorithm based on the low bound gets larger, factor of b into account, we find that the advantage of which means the former has more adaptability. Taking the proposed power allocation algorithms is more obvious under 1-bit quantization. In all, under different ADC configuration and transmit power, the proposed power allocation algorithms have great superiority over equal power allocation algorithm.

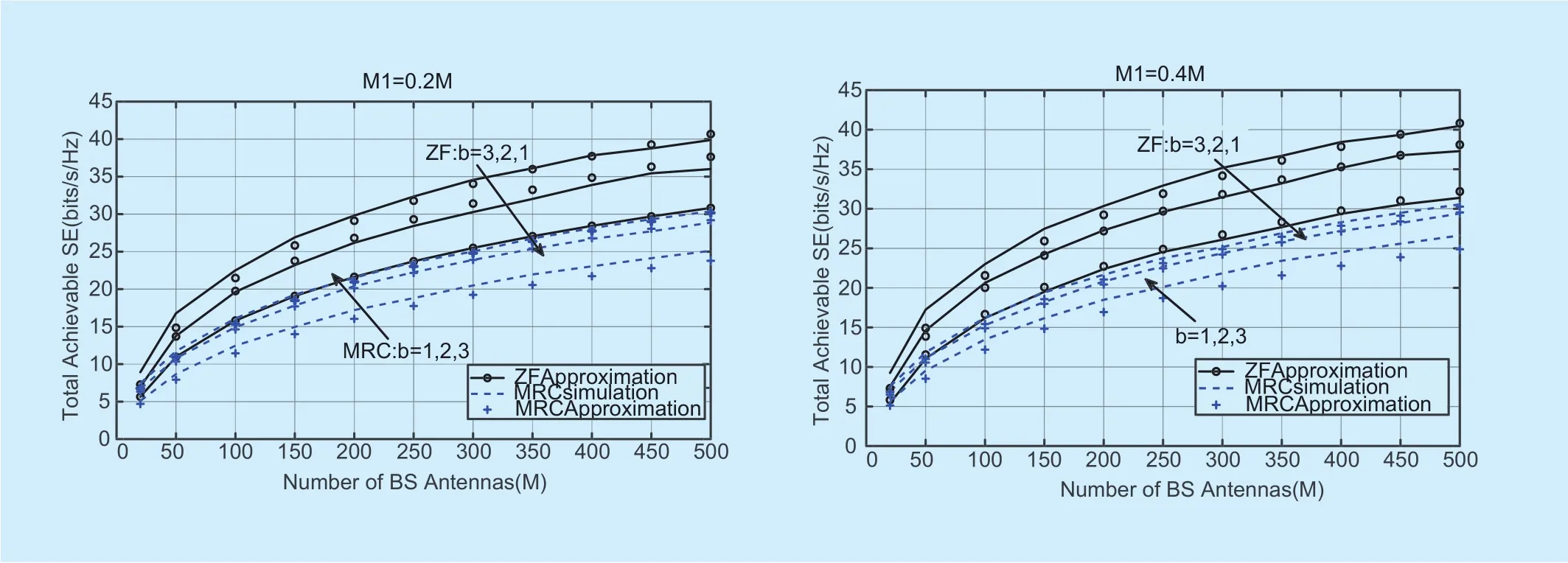
Fig. 4. Total achievable SE versus the number of antenna under various b with MRC and ZF detector.

In figure 4, we illustrate the theoretical achievable SE and its corresponding analytical approximation results versus the number of BS antennas for different ADC quantization bits with MRC and ZF detector in single-cell system with Rayleigh fading channel. At the same time, we take the proportion of full resolution ADCs into account and show the contradistinction using two graphs in figure 4.The average transmit power puis set as 10 dB here. We observe that the achievable SE increases with the number of BS antennas M and quantization bits b for both MRC and ZF detector. The figure showcases that the approximation of SE does not remain so tight with the simulated result for 1-bit quantization, especially with MRC detector, but as b grows,approximation can be considerably precise.It’s noted that ZF detector performs better than MRC detector when under the same ADC configuration, but the former brings about more calculation complexity and energy consumption inevitably. When the proportion of full resolution ADCs κ increases 0.2 to 0.4, we can see that the achievable increase roughly only by 2 bits/s/Hz at M=500 with b=1,2.Thus, increasing κ can be not worth in practise.

VI. CONCLUSION

This paper investigated the uplink achievable SE in multi-cell systems with MRC detector and in single-cell systems with ZF detector under perfect CSI. We obtained a closed-form expression of the achievable SE by considering the additive quantization noise. Analysis on the approximation of the achievable SE demonstrates that the achievable SE increases with the transmit power, the number of antennas, the proportion of full-resolution ADCs and quantization bits of the low-resolution ADCs. It is noteworthy that the improvement of the achievable SE can not be obtained by simply increasing the transmit power, since it can work on interference signals. Furthermore,we proposed the power allocation algorithms based on the lower bound and upper bound of approximate achievable SE for multi-cell systems with Rician fading channel under MRC detector. Comparing to the equal power allocation algorithm, simulation results proved that proposed power allocation algorithms remarkably improve the total achievable SE,which verifies the effectiveness of our proposed schemes.

ACKNOWLEDGEMENT

This work was supported in part by the National Science Foundation (NSFC) for Distinguished Young Scholars of China with Grant 61625106, the National Natural Science Foundation of China under Grant 61531011, the Hong Kong, Macao and Taiwan Science and Technology Cooperation Program of China(2016YFE0123100), and the Guangzhou University project under Grant 27000503123.

[1] H. Q. Ngo, E. G. Larsson, and T. L. Marzetta,“Energy and spectral efficiency of very large multiuser MIMO systems,” IEEE Trans. Wireless Commun., vol. 61, no. 4, pp. 1436-1449, Apr.2013.

[2] A. Fehske, G. Fettweis, J. Malmodin, and G.Biczok, “The global footprint of mobile communications: the ecological and economic perspective,” IEEE Commun. Mag., vol. 49, no. 8, pp.55-62, Aug. 2011.

[3] Weiqiang Tan, Shi Jin and Jide Yuan, "Spectral and energy efficiency of downlink MU-MIMO systems with MRT," in China Communications,vol. 14, no. 5, pp. 105-111, May 2017.

[4] Xiangming Li, Tao Jiang, Shuguang Cui, Jianping An, and Qian Zhang, “Cooperative Communications Based on Rateless Network Coding in Distributed MIMO Systems,” IEEE Wireless Commun., vol. 17, no. 3, pp. 60-67, Jun. 2010.

[5] W. Tan, M. Matthaiou, S. Jin, and X. Li, “Spectral efficiency of DFT based processing hybrid architectures in massive MIMO,” IEEE Wireless Commun. Lett., vol. 6, no. 5, pp. 586-589, Sep.2017.

[6] W．Tan, S. Jin, C. K. Wen, T. Jiang , “Spectral eきciency of multi-user millimeter wave systems under single path with uniform rectangular arrays,” EURASIP J. Wireless Comm. and Networking, vol.181,pp. 458-472, Nov. 2017.

[7] E. G. Larsson, O. Edfors, F. Tufvesson, and T. L.Marzetta, “Massive MIMO for next generation wireless systems,” IEEE Commun. Mag., vol. 52,no. 2, pp. 186-190, Jan. 2014.

[8] X. Yang et al., "Design and implementation of a tdd-based 128-antenna massive MIMO prototype system," in China Communications, vol. 14,no. 12, pp. 162-187, December 2017.

[9] R. H. Walden, “Analog-to-digital converter technology comparison,” in Proc. of 1994 IEEE GaAs IC Symposium, Oct. 1994, pp. 217-219.

[10] C.K. Wen, C.J. Wang, S. Jin, KK Wong, P Ting,“Bayes-optimal joint channel-and-data estimation for massive MIMO with low-precision ADCs,” in IEEE Trans. on Signal Process., vol. 64,no. 10, pp. 2541-2556, May. 2016.

[11] N. Liang and W. Zhang, “A mixed-ADC receiver architecture for massive MIMO systems,” in IEEE Information Theory Workshop (ITW), 2015, pp.229-233.

[12] A. K. Fletcher, S. Rangan, V. K. Goyal, and K.Ramchandran, “Robust predictive quantization:Analysis and design via convex optimization,”IEEE J. Sel. Topics Signal Process., vol. 1, no. 4,pp. 618-632, Dec. 2007.

[13] O. Orhan, E. Erkip, and S. Rangan, “Low power analog-to-digital conversion in millimeter wave systems: Impact of resolution and bandwidth on performance,” in Proc. Of Information Theory and Applications (ITA) Workshop, Jun. 2015, pp.191-198.

[14] L. Fan, S. Jin, C. Wen, and H. Zhang, “Uplink achievable rate for massive MIMO systems with low-resolution ADC,” IEEE Commun. Lett., vol.19, no. 12, pp. 2186-2189, Oct. 2015.

[15] W. Tan, S. Jin, C. K. Wen, and Y. Jing, “Spectral Eきciency of Mixed-ADC Receivers for Massive MIMO Systems,” IEEE Access., vol. 4, pp. 7841-7846, Sept. 2016.

[16] D. Qiao, W. Tan, Y. Zhao, C. K. Wen and S. Jin,“Spectral efficiency for massive MIMO zero-forcing receiver with low-resolution ADC,”in Proc. 2016 8th International Conference on Wireless Communications and Signal Processing(WCSP), Oct. 2016, pp. 1-6.

[17] L. Fan, S. Zhang, T. Q. Duong, G. K. Karagiannidis, “Secure Switch-and-Stay Combining(SSSC) for Cognitive Relay Networks,” IEEE trans.commun., vol. 64, no. 1, pp. 70-82, Jan. 2016.

[18] L. Fan, Shengli Zhang, Trung Q. Duong, George K. Karagiannidis, “On secrecy performance of MISO SWIPT systems with TAS and imperfect CSI,” IEEE Trans. Commun., vol. 64, no. 9, pp.3831C3843, Sep. 2016.

[19] L. Fan, X. Lei, N. Yang, T. Q. Duong, and G.K. Karagiannidis, “Secure multiple amplify-and-forward relaying with cochannel interference,” IEEE Journal of Selected Topics in Signal Processing, vol. 10, no. 8, pp. 1494-1505, Dec.2016.

[20] Lisheng Fan, Rui Zhao, Feng-Kui Gong, Nan Yang, George K. Karagiannidis, “Secure Multiple Amplify-and-Forward Relaying Over Correlated Fading Channels,” IEEE trans. commun., vol. 65,no. 7, pp. 2811 - 2820, Jul. 2017.

[21] T. C. Zhang, C. K. Wen, S. Jin and T. Jiang,“Mixed-ADC massive MIMO detectors: performance analysis and design optimization,” IEEE Trans. Wireless Commun., vol. 15, no. 11, pp.7738-7752, Nov. 2016.

[22] Q. Zhang, S. Jin, K. K. Wong, H. B. Zhu, and M.Matthaiou, “Power scaling of uplink massive MIMO systems with arbitrary-rank channel means,” IEEE J. Sel. Topics Signal Process., vol. 8,no. 5, pp. 966-981, Oct. 2014.

[23] S. Jin, W. Tan, M. Matthaiou, J. Wang, and K. K.Wong, “Statistical eigenmode transmission for the MU-MIMO downlink in Rician fading,” IEEE Trans. Wireless Commun., vol. 14, no. 12, pp.6650-6663, Dec. 2015.

[24] W. Tan, S. Jin, J. Wang, and Y. Huang, “Achievable sum-rate analysis for massive MIMO systems with diあerent array con figurations”, in Proc. IEEE Wireless Commun. and Networking Conference(WCNC), Mar. 2015, pp. 316-321.

[25] Q. Bai, A. Mezghani, and J. A. Nossek, “On the optimization of ADC resolution in multi-antenna systems,” in Proc. Of the Tenth Int. Symposium on Wireless Commun. Systems (ISWCS),Feb. 2013, pp. 1-5.

[26] J. Mo and R. Heath, “High SNR capacity of millimeter wave MIMO systems with one-bit quantization,” in Proc. Of Information Theory and Applications (ITA) Workshop, Mar. 2014, pp.629-635.

[27] B. Hassibi and B. M. Hochwald, “How much training is needed in multiple-antenna wireless links,” IEEE Trans. On Information Theory, vol.49, no. 4, pp. 951-963, Apr. 2003.

[28] L. Fan and S. Jin, “Low complexity power allocation algorithms for uplink of massive MIMO systems,” Journal of Southeast University (Natural Science Edition)., vol. 46, no. 1, pp. 7-12, May 2016.

[29] Q. Bai and J. A. Nossek, “Energy eきciency maximization for 5G multi-antenna receivers,” Trans.on Emerging Telecommun. Technologies. , vol.26, no. 1, pp. 3-14, Jan. 2015.

[30] A. Mezghani and J. A. Nossek, “Modeling and minimization of transceiver power consumption in wireless networks,” in Proc. Of 2011 International ITG Workshop on Smart Antennas , Apr.2011, pp. 1-8.

[31] S. Krone and G. Fettweis, “Achievable rate of single-carrier systems with optimal uniform quantization at the receiver,” in Proc. Of 2010 IEEE Information Theory Workshop, Jul. 2010,pp. 1-5.

[32] A. John, T . Tague, and C. I. Caldwell, “Expectations of useful complex wishart forms,” Multidimensional Systems and Signal Processing, vol. 5,no. 3, pp 263-279, Jul. 1994.

[33] F. Rusek, D. Persson, and B. K. Lau, “Scaling up MIMO: Opportunities and challenges with very large arrays,” IEEE Signal Process. Mag., vol. 30,no. 1, pp. 40-60, Jan. 2013.