Xiaofei Wang＊, Hongkun He, Yan Xu, Yang Lei

School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710072, China

* The corresponding author, email: wxf19910721@foxmail.com

I. INTRODUCTION

In recent years, with the rapid development of wireless communication technology, indoor positioning research steps into a new developing stage. Different wireless technologies have been successfully applied to indoor positioning, such as RFID [1], WIFI [2], Bluetooth[3], UWB [4] etc. Related industries based on indoor location services have emerged one after another. Indoor positioning technology plays an increasingly important role in social life.

At present, wireless indoor positioning is mainly based on fingerprint and ranging,which can achieve the positioning accuracy of 3～4 meters [5]. Compared with the fingerprint-based positioning technology, the positioning technology based on ranging has no requirement for establishing a complex fingerprint database, and can achieve higher positioning accuracy. So it has a wider application prospect [6]. Time of arrival (TOA)is the most widespread ranging technology,whose principle is to get range between the transmitter and the receiver by measuring the signal propagation time [7-8]. The positioning method based on TOA is to calculate the position coordinates of the mobile terminal (MT)through certain mathematical methods while obtaining the desired range. Therefore, the accuracy of TOA ranging will directly affect the accuracy of the indoor positioning.

Range-based positioning error is determined by the geometry position distribution of the access points (APs) and MT [9] as well as the ranging accuracy. In a wireless network,when the positions of APs are fixed, the positioning error of the MT at different positions will vary widely, which makes the positioning system highly unstable and unreliable. Most studies have focused on this issue and the Automatic Precision Control (APC) algorithm proposed in [9] can be used as a good solution. So the work in this paper concentrates on improving ranging quality.

In the implementation of positioning, the complexity of the indoor channel obstructs the accuracy of ranging. Multipath [10] and NLOS[11] propagation etc. in the channel will cause a clear error for ranging, and have a negative effect on positioning accuracy. It is a great challenge for the indoor positioning system to reduce the ranging error and improve the positioning accuracy. The ranging error could be reduced by using ranging redundancy as in [12]. The method reduces the ranging error by sacri ficing the number of positioning APs,which obviously does not meet the positioning requirements of low cost. The authors in [13]proposed a method of ranging error correction according to the ranging error classification based on received signal strength indicator(RSSI). However, it is difficult to ensure the accuracy of the RSSI measurements in actual positioning, resulting in the real effect of the method is not ideal. The method we proposed performs a ranging data correction by taking advantage of the characteristics and related parameters of the TOA ranging error model(TREM) and effectively avoids the existing problems of the methods in [12] and [13]. The experiment results show that the method can greatly reduce the effect of ranging errors on the positioning accuracy, as well improve the positioning performance.

The remainder of this paper is organized as follows. In Section II, we discuss the ranging error distribution under the WIFI indoor channel and build the TREM. In Section III,the method of ranging error correction is described in detail, while the experiments and the simulation results are presented in Section IV. Finally, a conclusion is drawn in Section V.

In this work, we have proposed a ranging error correction method based on a prior error model for wireless indoor environments.

II. RANGING ERROR DISTRIBUTION AND MODELING

The actual indoor channel is so complex, but in terms of ranging, the multipath and NLOS propagation are the major factors that affect the accuracy of ranging. Though different wireless channels have different ranging error distributions, the effects of multipath and NLOS propagation on different channels are similar to a certain extent. In this paper, we consider the WIFI indoor channel to explore the ranging error distribution characteristics and then build the TREM.

2.1 Ranging error distribution characteristics

Fig. 1. The ranging error distribution diagrams. (a) Transceiver distance=20m. (b) Transceiver distance =30m.

Figure 1 shows the ranging error distribution characteristics on different transceiver distanc-es [14-15]. According to figure 1, the TOA ranging error under the WIFI indoor channel has the following characteristics: first of all,the ranging error value is positive and has an upper limits; then, the characteristic of the ranging error spatial distribution is spatial centrality and most of the errors are concentrated in a certain interval, indicated in the figure 1 by red dotted lines, that means the ranging errors beyond the interval make up a very small fraction; besides, the ranging error is related to the transceiver distance and in general, the mean value of the ranging error increases with the increase of the transceiver distance.

2.2 Modeling the ranging error

The construction of the accurate TREM can provide more effective information for reducing the ranging error and improving the indoor positioning accuracy. Modeling the ranging error generally includes the following steps: as the ranging error is related to transceiver distance, the sample frequency histogram of the ranging error on different transceiver distances needs be established first; find or construct a function curve p()ε (ε is the ranging error value) to achieve the best distribution fitting for the sample data. figure 1 illustrates that the distribution characteristics of the ranging error is very similar to that of Rice or Normal,so the probability density function (PDF) of Rice, Normal, or their mixed distribution can be used as a priori condition to get the p()ε.Thus, the ranging error is modeled, and p()ε is the function representation of the TREM.

III. RANGING ERROR CORRECTION

In practical application, the TREM and its PDF p()ε in real positioning scenarios can be obtained through the field measurement.Combining p()ε with the specific localization process, regarding a certain characteristic parameter of the TREM as the ranging error correction value (RECV) and adjusting the RECV reasonably, ranging data is corrected successfully.

3.1 Principle of the ranging error correction

The target positioning equation based on TOA is as follows:

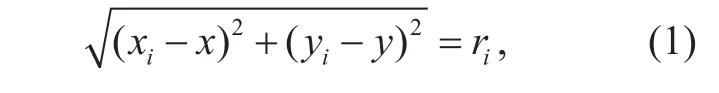
where (x, y) is the coordinate of the MT to be estimated; (xi, yi) is the coordinate of the i-th access point (APi) which is already given;riis the measured value of distance between the MT and APi. Since riis subject to error, it can be expressed as:

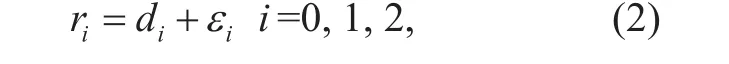
where diis the truth value of distance between the MT to APiand εiis the corresponding ranging error.

The purpose of ranging error correction is to reduce the ranging error and make the corrected riequal to the dias much as possible.Based on the ranging error compensation, a prior parameter μican be used as the RECV to correct the riand then the corrected TOA ranging value ri?can be obtained as below:

Let E [ ] indicate the expectation of the corresponding variable. In order to improve the ranging accuracy,is required whenever possible. Then, μiis given by:

In summary, when μi=E [εi] the expectation ofexactly equals to di. In other words, the mean value of the TOA ranging error changes from E [εi] to 0. Also, the ranging error distributes centrally around the mean value, depending on the distribution characteristics of the ranging error. Thus, the ranging error is effectively reduced.

3.2 Estimation of the RECV

According to the ranging error distribution characteristics, the ranging error tends to be concentrated in a certain interval, and the ranging error beyond the interval represents a tiny fraction, which means it is almost impossible for the ranging error to drop out of the interval in only one ranging process. As, a more effective μicould be obtained by means of considering the ranging error within the interval and sacri ficing the ranging error out of the interval while calculating the E [εi].

A interval function g(εi) is de fined to represent the solution interval of μiand it can be expressed as:

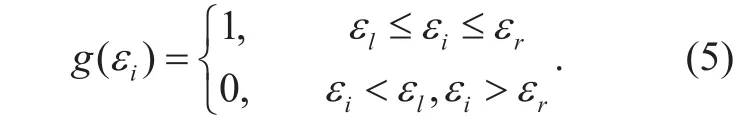
εland εrwhich are the essential parameters of g(εi) can be obtained by the following methods.

Assume that the probability of the ranging error εiin the error interval [εl, εr] is 1?α where α means the interval probability parameter. That is,

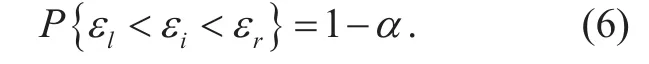
Eq. (6) can be rewritten as:

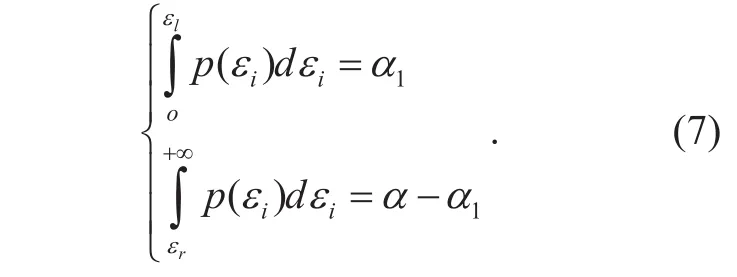
There are many combinations of εland εrsatisfying eq. (7) with different values of α and α1. In the actual process of ranging error correction, α and α1can be selected based on the distribution characteristics of the ranging error. Then εland εrare determined and the expression of g(εi) is uniquely obtained.Finally the RECV μican be estimated by:

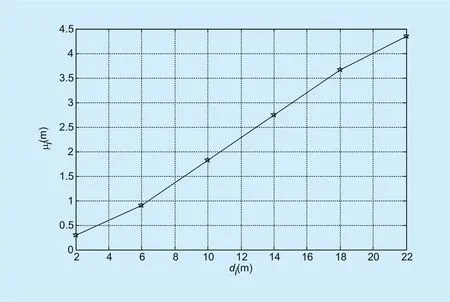
Fig. 2 The fitting curve between di and μi.

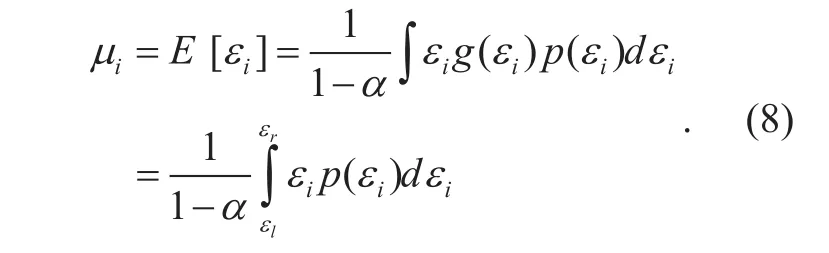
3.3 Primary correction of the ranging error

With the truth TOA ranging value diand its corresponding RECV μihave been known,the curve fitting method can be used to obtain the function expression for diand μilikeμi=f( di). The functional relationship curve[15] between diand μifor typical measurement cases has been plotted in figure 2. It’s worth mentioning that the function expressionμi=f( di) can be mathematically modeled as a piecewise linear function.

When correcting the ranging data ri, theμicannot be obtained directly since the diis unknown. But based on the fact that the corrected TOA ranging value≈di, the function expression μi=f( di) can be replacedis established. Letand then the ri?is given by:

3.4 Adjustment of the RECV

The geometric pattern described by eq. (1) is a circle, namely the positioning circle, where the AP is equivalent to the circle center and the ranging value rirepresents the circle radius. When solving the equation by using the geometric algorithm, it is necessary to find the intersection between any two circles. While the primary correction of TOA ranging error has been achieved, there must be unreasonable corrections for some ranging data, resulting in no intersection between the two circles, which means the equation has no solutions. In order to solve this problem, the RECV μishould be adjusted.

Having done the ranging error primary correction (the RECVs are μiand μj, respec-tively), the radii of any two positioning circles can be expressed as ri?and rj?, respectively(i, j=0,1,2,i≠j). To quantitatively discuss the process of the adjustment of the RECV, we de fine the RECV adjusting function which is used to get a reasonable RECV as:

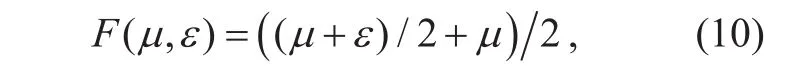
where μ is the current RECV, ε means εlor εrde fined in eq. (5) and the value of F(μ,)ε represents the adjusted RECV. When ε=εl,F(μ,)ε＜μ and F(μ,)ε＞μ while ε=εr.The RECV should be adjusted to become smaller or larger, basing on the geometric position relationship of the positioning circles, so as to make the positioning circles intersected.Suppose M is the maximum number of adjustments for the RECV and a counter m is set for recording the number of adjustments. Then,the speci fic method of adjusting the RECV is as follows:

6) If m＞M, it is considered that the adjustment of the RECV does not reach the expected effect. At this point, the ranging data needs to be re-obtained and re-corrected.

The adjustment of the RECV is realized through the above steps, which effectively solves the problem that the positioning equation has no solutions because of the limitation of the ranging error primary correction.

IV. EXPERIMENTS AND RESULTS

Two experimental evaluations are carried out to demonstrate the superiority of the proposed method. The first experiment evaluates the overall performance of the ranging error correction method from the perspective of ranging and positioning for different interval probability parameters. The second part validates the necessity of adjusting the RECV from the view of algorithm performance.

4.1 In fluence of the ranging error correction on TOA ranging and positioning

In this experiment, three APs are deployed and the locations of AP0to AP2are (25, 25),(25, 75), and (75, 25), respectively. The MT is positioned once per meter in the 2D plane(x∈[30,70],y ∈[30,70]). The distance between the MT and APi(i=0,1,2) is regarded as the TOA ranging value. We use the mean square error (MSE), mean absolute error(MAE) and cumulative distribution function(CDF) as the performance index of the method.

According to the analysis presented in Section III, the value of most ranging errors is approximately equal to the RECV. When the ranging data is corrected by the RECV, it is very possible for the MT to reduce the ranging error meanwhile improving the positioning performance, which is supported by the following simulation results.

The TOA ranging and positioning errors for both the uncorrected and corrected ranging data are present in Table I. The results show the ranging and positioning are found to perform better when the proposed method is applied which clearly fits the theoretical analysis. In the case of (α, α1)=(0.15,0.05), withranging error correction, the MSE and MAE for ranging have been reduced by 87.7% and 64.1%, respectively. Moreover, the MSE and MAE for positioning have been reduced by 88.2% and 65.2%, respectively.

Table I. The variation of TOA ranging and positioning error before and after ranging error correction.

In general, the MSE and MAE do not fully represent the real performance of a positioning system. Considering the RECV is related to the parameters of α and α1, figure 3 and figure 4 show the CDFs of the TOA ranging and positioning errors, respectively for different values of α and α1in order to provide more information. The improvement degree of ranging and positioning performance is different with the changes of α and α1. It can be seen that the best performance is achieved under the condition of (α, α1)=(0.15,0.05). This result is not surprising because the performance of ranging and positioning depends on an effective estimate of RECV, which was achieved according to α and α1through eq. (8). In order to re flect the distribution characteristics of the ranging error as much as possible, the value of α should not be too large and it varies from 0.05 to 0.20 in this experiment. Besides,α1≤α is required to determine the εland εr. When (α, α1)=(0.15,0.05), after ranging error correction, the possibility of the ranging error below 1m is increased from 17.91%to 47.89%; the possibility of the positioning accuracy better than 1m is increased from 17.31% to 48.19% and in particular the fact that positioning errors above 3m have almost been eliminated.

In addition, note the general improvement of ranging error values and positioning error values for the corrected ranges no matter what the values of α and α1are. This observation is consistent with the expectation, which illustrates the generality of the proposed method.

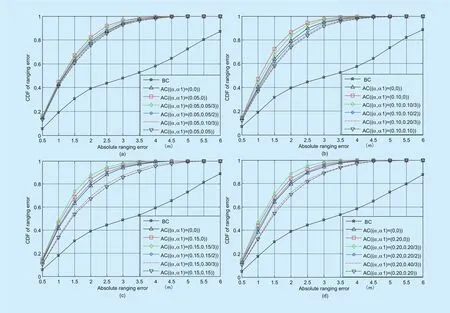
Fig. 3. CDFs of the TOA ranging error before and after applying our proposed ranging error correction method. (a) α=0.05. (b)α=0.10. (c) α=0.15. (d) α=0.20.

Fig. 4. CDFs of the TOA positioning error before and after applying our proposed ranging error correction method. (a) α=0.05. (b)α=0.10. (c) α=0.15. (d) α=0.20.

Above all, the ranging error correction method proposed in this paper plays a good inhibitory effect on the TOA ranging error,and greatly improves the accuracy of indoor positioning.

4.2 In fluence of the RECV adjustment on the algorithm performance

In this part, the deployment of the APs is the same as the last experimental. The MT is positioned at the interval of 0.5m,1.0m and 1.5m respectively in the plane area with 40x40m2. Count the number of the equations without solutions (Num) and the ratio of the equations in total (Rat) before and after the adjustment of the RECV.

is de fined as the gain reference value to indicate the improvement degree of the problem having no solutions for equations.

Table II shows the number of the equations without solutions for both the non-adjusted and adjusted RECVs while M=2. There are a great number of unsolvable equations and such equations occupy a large ratio in total before adjusting the RECV. However, we can see the number of the equations without solutions is signi ficantly decreased, and the ratio of such equations is reduced from about 40% to about 6%. What’s more the gain reference value is almost 8dB, which means a great improvement for this problem.

Figure 5 illustrates the variation of Rat with different values of M. It is clear that Rat de-creases rapidly with the increase of M. When M=8, the Rat is reduced to 0, that is to say, all positioning equations have solutions. A right value of M can be obtained according to the actual positioning requirements.

Table II. The difference of the number of equations without solutions

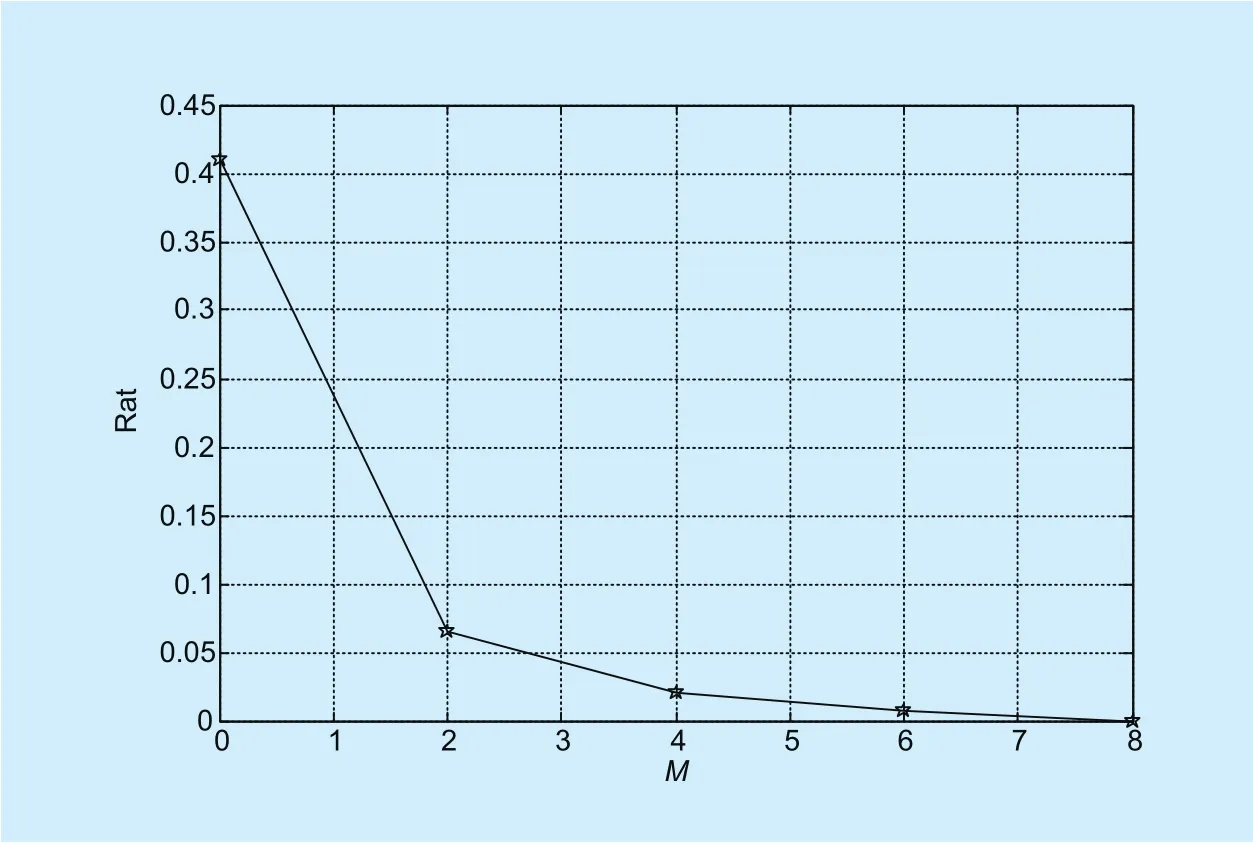
Fig. 5. The variation tend of the Rat with M.

In a word, It is very effective for the adjustment of the RECV to solve the problem which the equations have no solutions, reduce the number of repeated ranging and improve the algorithm performance.

V. CONCLUSION

In this work, we have proposed a ranging error correction method based on a prior error model for wireless indoor environments. Specifically, we take the WIFI indoor channel as an example to study the ranging error distribution characteristics and then set up the ranging error model whose function expression is p()ε.Moreover, we find that the mean value of ranging error in a certain interval is an important parameter related to the ranging accuracy of TOA. Afterwards, the mean value is regarded as the RECV and it is adjusted according to the geometric position relationship of any two positioning circles. The ranging data correction is realized finally. Experimental results demonstrate that the three major indicators including MSE, MAE and CDF that reflect the TOA ranging and positioning performance have been signi ficantly improved, namely the proposed method can effectively reduce the ranging error.

ACKNOWLEDGEMENTS

This work was supported in part by Huawei Innovation Research Program (Grant No.YB2013020011).

[1] R. O. Warther, “Printed planar RFID element wristbands and like personal identi fication devices,” U.S. Patent No. 8,636,220, Jan. 2014.

[2] T. Adame, A. Bel, B. Bellalta, J. Barcelo, and M.Oliver, “IEEE 802.11 ah: the WiFi approach for M2M communications,” IEEE Wireless Communications, vol. 21, no. 6, 2014, pp. 144-152.

[3] D. M. Sangster, C. M. Dreher, J. K. Ngari, C. Manzanedo, and J. C. Marshall, “Systems and methods for pairing bluetooth devices,” U.S. Patent No. 9,363,253, Jun. 2016.

[4] H. K. He and H. S. Shi, “Asynchronous UWB localization method and algorithm for multiple targets,” Journal of System Simulation, vol. 20,no. 7, 2008, pp. 1713-1715+1733.

[5] D. Lymberopoulos, J. Liu, X. Yang, R. R. Choudhury, V. Handziski, and S. Sen, “A realistic evaluation and comparison of indoor location technologies: Experiences and lessons learned,”Proc. Proceedings of the 14th international conference on information processing in sensor networks, 2015, pp. 178-189.

[6] A. Günther, and C. Hoene, “Measuring round trip times to determine the distance between WLAN nodes,” Proc. International Conference on Research in Networking, 2005, pp. 768–779.

[7] K. A. Denney, M. Hamada, Y. Nagao, M. Kurosaki, and H. Ochi, “ToA-based positioning system for industrial wireless LAN,” Proc. Intelligent Signal Processing and Communication Systems (ISPACS), 2016 International Symposium on, 2016,pp. 1-5.

[8] M. Llombart, M. Ciurana, and F. Barcelo-Arroyo,“On the scalability of a novel WLAN positioning system based on time of arrival measurements,”Proc. Positioning, Navigation and Communica-tion, 2008. WPNC 2008. 5th Workshop on, 2008,pp. 15–21.

[9] S. Han, Z. Gong, W. Meng, C. Li, and D. Zhang,“Automatic Precision Control Positioning for Wireless Sensor Network,” IEEE Sensors Journal,vol. 16, no. 7, 2016, pp. 2140-2150.

[10] H. Mazhar, and S. A. Hassan, “Analysis of target multipaths in WiFi-based passive radars,” IET Radar, Sonar & Navigation, vol. 10, no. 1, 2016,pp. 140-145.

[11] X. H. Li, X. Cai, Y. Q. Hei, and R. Y. Yuan, “NLOS identi fication and mitigation based on channel state information for indoor WiFi localization,”IET Communications, vol. 11, no. 4, 2017, pp.531-537.

[12] D. C. Popescu, and M. Hedley, “Range data correction for improved localization,” IEEE Wireless Communications Letters, vol. 4, no. 3, 2015, pp.297-300.

[13] J. He, Q. Wang, Q. X. Zhang, B. F. Liu, and Y. W.Yu, “A practical indoor TOA ranging error model for localization algorithm,” Proc. Personal Indoor and Mobile Radio Communications (PIMRC),2011 IEEE 22nd International Symposium on,2011, pp. 1182-1186.

[14] E. Almazrouei, N. Al Sindi, S. R. Al-Araji, N. Ali, Z.Chaloupka, and J. Aweya, “Measurements and characterizations of spatial and temporal TOA based ranging for indoor WLAN channels,” Proc.Signal Processing and Communication Systems(ICSPCS), 2013 7th International Conference on,2013, pp. 1-7.

[15] J. He, Y. S. Geng, C. Xu, Z. S. Han, and S. H.Duan, “Height dependent TOA ranging error model for near ground localization applications,” Proc. Personal, Indoor, and Mobile Radio Communication (PIMRC), 2014 IEEE 25th Annual International Symposium on, 2014, pp. 2045-2050.