Caihong Kai, Shengli Zhang＊, Lusheng Wang

1 School of Computer Science and Information Engineering, Hefei University of Technology, Hefei 230000, China

2 Department of Communication Engineering, Shenzhen University, Shenzhen 518000, China

* The corresponding author, email: zsl@szu.edu.cn

I. INTRODUCTION

With the rapid deployment of WLANs, it is common today to find multiple 802.11-like networks physically co-located with each other, forming a large-scale wireless network in which links interact and compete for airtime according to the carrier-sensing multiple access (CSMA) protocol. Under CSMA, when a node senses the channel busy, it will refrain from transmission in order to avoid packet collision.

The carrier-sensing relationships among nodes are often “non-all-inclusive” in that each node may sense only a subset of the other nodes and different nodes sense different subsets, leading to drastically different obtained throughputs.Throughput analysis of such a practical network has attracted much interest from the community. Recent tutorial paper [1] summa-rized the performance analysis on “non-all-inclusive” CSMA networks and prior work can be traced there. Although the dependencies and interactions among links (such as carrier sense, frozen and random backoff) in a CSMA network has been well investigated and understood by the research community through a continuous-time Markov model [1-3], packet collisions incurred by simultaneous transmissions have not been captured in such models.On the other hand, in practical 802.11-like networks (such as IEEE 802.11 [4]), the time is divided into discrete mini-slots, and collisions happen if multiple con flicting links backoff to zero in the same timeslot during their backoff process and then transmit simultaneously1When a collision occurs, we assume that all the involved links’packets fail of reception and will attempt to retransmit later..Thus, it is desirable to move forward to explore how collisions in such a network will affect system performance and this paper makes such an attempt.

This paper proposes an Extended Ideal CSMA Network (EICN)model to characterize the collision effects as well as the interactions and dependency among links in the network.

More specifically, we propose an EICN model to capture the effects of collisions caused by two or more transmissions initialized in the same mini-timeslot2The “hidden-node”phenomenon can also cause packet collisions.That is, the transmitters of two links cannot hear the activities of each other, but a collision occurs if the two transmissions overlap. The throughput analysis with collisions incurred by “hidden-node” is left as future work in this paper. Alternatively, we can design protocols, such as the algorithms proposed in[5], to remove the “hidden-node” collisions.. The basic idea of EICN is as follows: observing the fact that collisions can only occur in a state when two or more neighbor links actively count down,we identify all the states when there are two or more neighbor links actively counting down simultaneously. We refer to these states as“collision-stemmed” states because only such states could lead to a collision event. By enumerating all the “collision-stemmed” states as well as the corresponding collision states and analyzing the transition probabilities between states, we could construct a collision-captured state-transition diagram, based on which the link throughputs and collision probabilities of each link can be computed. Simulation results show that the EICN model is of high accuracy. Under various network topologies and protocol parameter settings, the computation error of link throughputs using EICN is kept to 4% or below. Interestingly, we find that unlike expected, the effect of collisions on link throughputs in a modest CSMA wireless network is not significant. For example, in a network in which a link has on average three to four neighbors, the link throughputs do not vary much when collision events are taken into account. This observation enriches our understanding on practical CSMA wireless networks such as Wi-Fi: for a CSMA network in which each link has three to four neighbors, collisions occur while do not affect link throughputs significantly. Thus, in practical WLAN design, it is not necessary to sacri fice throughput performance by increasing the contention window size to avoid collisions.

Related Work

As far as collisions in CSMA wireless networks are considered, Ref. [6] presented a two-dimensional model for IEEE 802.11 networks, assuming the “all-inclusive” case in which all links can sense each other. Unfortunately, it is prohibitive to extend the analysis of [6] to the “non-all-inclusive” case since the network state space becomes intractable due to the heterogeneous behavior of links.

For “non-all-inclusive” CSMA networks,most prior work focused on the continuous time Markov network (CTMN) [1-3] and elegant optimization algorithms are proposed to improve system performance [7,8]. In particular, Ref. [2] proposed an ICN to characterize the interactions and inter-dependencies among links and gave the closed-form expressions of link-throughputs. As shown in [2], the link throughputs can be obtained by the CTMN model although the system process is in fact not Markovian. Ref. [3] studied the capacity region of wireless CSMA/CA multihop networks. Based on the ICN model, the authors of [7,8] proposed elegant adaptive algorithms(ACSMA) for CSMA wireless networks to achieve system utility maximization under the pairwise model and SINR model, respectively.Inspired by the analysis of ICN, a Markovian approximation method was proposed in [9]to solve a set of combinational optimization problems in wireless networks. The temporal starvation phenomenon of CSMA networks was studied in [10]. The authors of [11,12]studied AP placement and AP selection algorithms for WLANs, respectively. Ref. [13]analyzed the throughput analysis and channel assignment in 802.11n and 802.11ac networks with the channel bonding technique. However, an important assumption made in prior analytical work above is that carrier-sensing is perfect and instantaneous. Thus, there is no collision in the network.

Observing that collisions happen in practical CSMA wireless networks, in this paper we will propose the EICN model to incorporate the effects of packets collisions caused by simultaneous transmissions. The link throughputs and collision probabilities can be computed under EICN. Finally, Ref. [14] adopted a decoupling method and derived closed-form throughput expressions for CSMA networks with hidden terminals. We note that [14] is based on a different set of assumptions and modeling techniques. For example, the authors assumed that the successful transmission probability of a link is independent of current system state while we remove this assumption in our analysis.

The remainder of the paper is organized as follows: Section II brie fly reviews the ICN model as well as the collision-free throughput analysis, and then proposes our EICN model. Section III presents the construction of the state-transition diagram under EICN and demonstrates how to compute link throughputs and collision probabilities. Experimental evaluations are performed in Section IV to examine the accuracy of our EICN computation.Finally, Section V concludes the paper.

II. SYSTEM MODEL

This section gives a brief review on the collision-free throughput analysis and then presents our EICN model.

2.1 ICN model (collision-free model)

In ICN [2], the carrier sensing relationship among links is described by a contention graph G=(V,E), where each link (a transmitter-receiver pair) is represented by a vertex i∈V while edges are used to capture the carrier-sensing relationships among links. At any time, a link has two possible states, active or idle. A link is active if there is a data transmission between its two end nodes. A link sees the channel as idle if and only if none of its neighbors is active.

Each link i in the network maintains a backoff timer, Ci, the initial value of which is a random variable tcd. The timer decreases in a continuous manner with dCi/dt =?1 as long as the link senses the channel as idle. The countdown process is frozen (dCi/dt=0) if the channel is sensed busy, and the countdown continues (dCi/dt =?1) with Ciinitialized to the previous frozen value upon the channel becomes idle again. When Cireaches zero,the link transmits a packet. We assume the transmission duration is a random variable ttr.After the transmission, the link resets Cito a new generated value and the process repeats.We de fine the access intensity of link i as the ratio of its mean transmission duration to its mean backoff time: ρi=Ei[ttr]/Ei[ tcd].

Let si∈{0,1} denote the state of link i,where si=1 if linki is active (transmitting)and si=0 if link i is idle (actively counting-down or frozen). The overall system state of ICN is s=s1s2...sN, where N is the number of links in the network. The collection of feasible states corresponds to the collection of independent sets (ISs) of the contention graph[15].

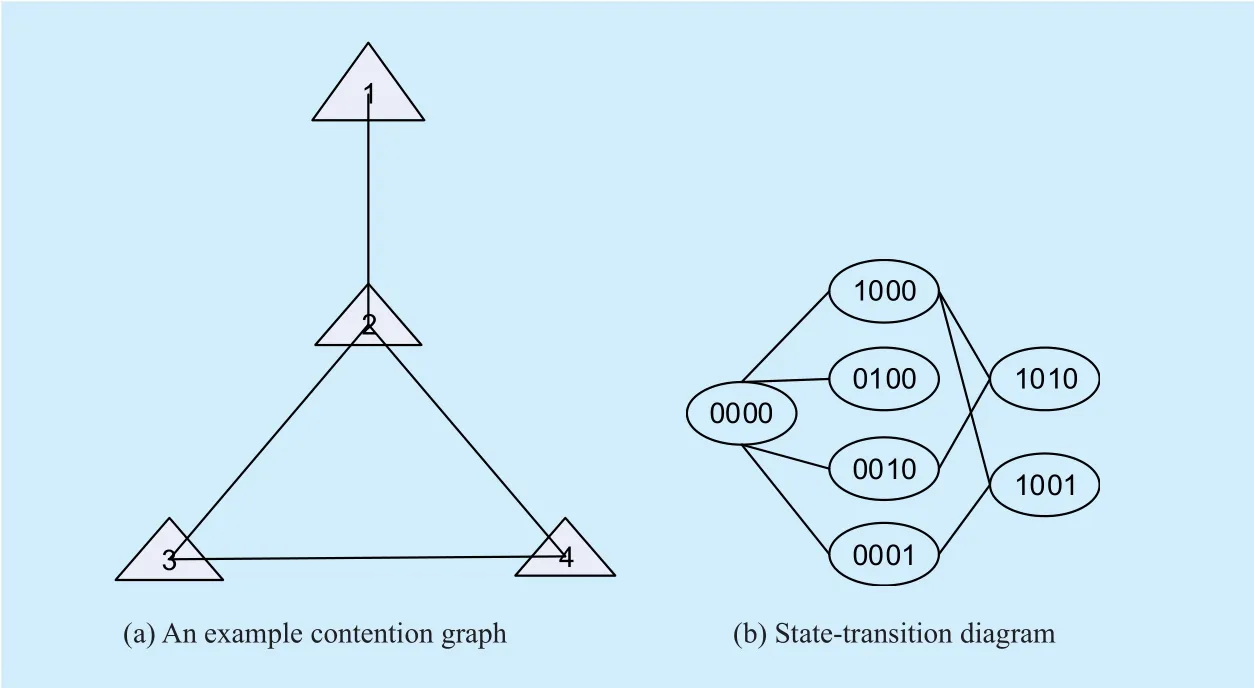
Fig. 1. (a) An example contention graph and (b) its state-transition diagram.

As an illustrating example, figure 1(a)shows a four-link CSMA network in which link 1 only senses link 2 while links 2, 3, and 4 can hear each other, and figure 1(b) shows the associated state-transition diagram3To avoid clutters, we have merged the two directional transitions between two states into one line in figure 1(b).Each transition from left to right corresponds to the beginning of the transmission of one particular link, while the reverse transition corresponds to the ending of the transmission of that link..

2.2 Throughput analysis under ICN

If we assume that both backoff time and transmission time are exponentially distributed, then s( t) is a time-reversible Markov process. For any pair of neighbor states in the continuous-time Markov chain, a transition from the left state to the right state occurs at rate λi=1/Ei[ tcd], and a transition from the right state to the left state occurs at rate μi=1/Ei[ ttr].

Let S denote the set of all feasible states.From [2], the stationary distribution of state s can be written as

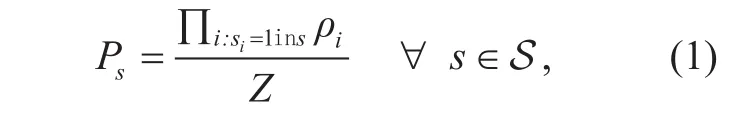
The fraction of time during which link i transmits is thi=∑s:si=1Ps, which corresponds to the normalized throughput of link i.

The above analytical throughputs have been adopted in several prior work and elegant algorithms have been proposed to analyze and optimize the CSMA wireless protocol [3], [7-10], [13]. However, collisions are unavoidable in practical 802.11-like networks since the backoff process is performed in discrete minitimeslots and the propagation delay is non-zero. We next describe our EICN model and attempt to investigate how such collisions affect the system performance in modest practical CSMA networks.

2.3 EICN model with collisions

In EICN we remove the “collision-free” assumption in ICN. Specifically, in EICN the time is divided into mini-timeslots. Link i maintains a backoff timer, Di, the initial value of which is an integer variable that is uniformly distributed between [0, CWi], where CWiis the size of the contention window [4]. The timer decreases by one for each timeslot when the link senses the channel as idle. Also, the backoff process is frozen when the channel is sensed busy. When the timer reaches zero, the link transmits a packet. We assume that the packet transmission duration is a fixed value equal to Ttrmini-timeslots. The other parts of the protocol are similar to the ICN model.Thus, in EICN, the access intensity of a link is ρ=2Ttr/CW4It is necessary to note that the analysis in this paper can be easily extended to the case in which links have diあerent access intensities..

It is important to note that different from ICN in which the feasible state is the ISs of the contention graph (i.e., no collision events), in EICN multiple links can backoff to zero in the same mini-timeslot and transmit simultaneously. That is, the states of two neighbor links, siand sjcan both be 1 at the same time. When a collision happens, we assume the two collided packets are lost5We do not consider the“signal capture” effect observed in [16].. Furthermore, to make the analysis tractable, we make the following two assumptions:

Assumption 1: No matter whether the last transmission is successful, the newly-generated backoff timer is initialized to a random integer that is uniformly distributed between [0,CWi]. That is, the contention window is NOT doubled upon collisions.

Assumption 2: The transmission time is fixed to length of Ttrmini-timeslots. This corresponds to the case in which the upper-layer applications running on top of the CSMA wireless network are of a unique type, e.g.large file-downloading, VoIP and so on.

To justify Assumption 1, we will show that the impacts of the contention-window-doubling mechanism are not signi ficant for modest CSMA networks through extensive simulations in Section IV. Note from Assumption 2 that in EICN, the links involved in a collision are “synchronized”. That is, both links involved in a collision must begin transmission in the same timeslot and will end transmission in the same timeslot after Ttrtimeslots. It can be shown that under this assumption, the system process is still time-reversible. We note that Ref. [7] made the same assumptions to design CSMA-based scheduling algorithms.Different from [7] where a new scheduling algorithm was proposed, this paper focuses on the throughput analysis of widely-deployed CSMA protocols such as WLANs.

Let qndenote the collision probability of a particular actively-countdown link with n actively-countdown neighbors. We have

III. THROUGHPUT ANALYSIS UNDER EICN

The outline of throughput analysis under EICN is as follows: among the ISs of the contention graph, we first identify all the states starting from which a collision may occur (referred to as the collision-stemmed states). For each such state, we can identify the transition rates between it and its neighbor states, and then construct a collision-captured state-transition diagram, from which we can compute the stationary probability of each state, the collision probabilities of each link, and finally obtain the normalized link throughputs.

In Part 3.1 below, we calculate the conditional collision probability beforehand, which will be used in the analysis of Part 3.2.

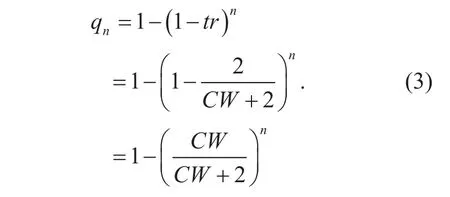
Take the typical value of contention window in IEEE 802.11b network, CW=31,as an example, the average distance between two transmission time slots is 15.5, and the transmission probability of an actively counting-down station over each timeslot is tr=1/ 16. 5 . The probability of collision starting from a state s with n+1 actively counting-down links is then 1?(15. 5/ 16. 5)n.Furthermore, from (3), we have

3.1 Conditional collision probability

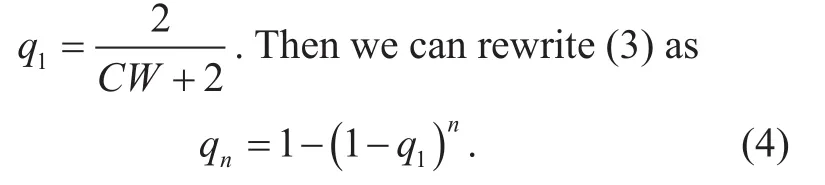
We note that for each collision event incurred when two or more neighbor links backoff to zero in the same mini-timeslot and transmit together, the multiple neighbor links involved in the collision must be actively counting-down before the collision occurs. We next compute the collision probability of a particular link with n actively-countdown neighbors.

Let us look at the mini-timeslots in which the link is not frozen (i.e., no neighbor links of the link is transmitting). The link alters between actively counting-down and transmitting over these mini-timeslots. Denote the transmission probability of an actively counting-down station over each timeslot by r. Recall that in EICN the backoff countdown time of each link is uniformly distributed between[0, CW], if we treat transmission slot as one countdown backoff slot6In CSMA network the system time is synchronized among different links, and each link determines whether to transmit only at the beginning of each mini-timeslot. Thus,the real packet transmission time is not important when calculating the transmission probability and we can treat the transmission time as one countdown backoff minitimeslot in the analysis., then the average distance between two transmission time slots is CW/2. Thus, the transmission probability of an actively counting down station over each timeslot is

As will be seen in Part 3.2, (4) is used in our algorithm to compute the transition rates between the collision states and its neighbor states.

Remark 1: Filling in the typical value of CW=31, the typical value of q1is 0.0607.When q1is small (such as the typical value of 0.0607), q12is rather smaller. Thus, for quick computation we could approximate qnas

3.2 Construction of the collisioncaptured state-transition diagram

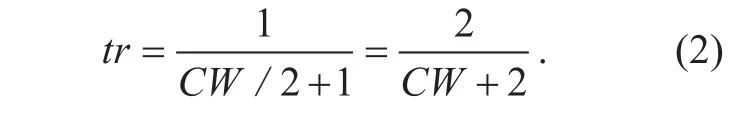
We next construct a state-transition diagram that captures the collision events. Speci fically,we first identify all possible collision-related states under EICN and construct a complete state-transition diagram, based on which we can compute the stationary probability of each state, the collision probability of each link,and obtain the normalized link throughputs.

3.2.1 System states of EICN

Definition of Collision-stemmed states:for each IS of the contention graph, if there are two or more neighbor links that are actively counting-down, we call this IS a collision-stemmed state.

Collision only occur starting from a collision-stemmed state in EICN. Take the network in figure 1 as an example, collision events only occur when the system is in state 0000 or 1000. In state 0000, all links are actively counting-down and each pair of the neighbor links in the contention graph may collide with each other. Similarly, in state 1000, links 3 and 4 have the chances to suffer from a collision,while the other states cannot lead to a collision because no two or more neighbor links are actively counting-down.

By enumerating all the ISs of the contention graph, we can identify all the collision-stemmed states and construct a new state-transition diagram GC. Denote the set of collision-stemmed states by M, for each s∈M, the collision states connected to s are represented by a single state, denoted by COLS. State COLSincludes all possible states in which a two-link collision occurs from state s, and the stationary probability of state COLSis the sum of the probabilities of these states.In the network of figure 1, M={0000 ,1000},a n d COL0000={1100, 0110, 0101, 0011},COL1000={1011}. Table 1 lists the collision-involved states of the network shown in figure 1.

Remark 2: It is important to note that in practical CSMA wireless networks the number of neighbors does not grow with the network size, thanks to geographical constraints, power control and orthogonal channels. Typically, in WLANs a link usually has no more than six neighbors regardless of the number of nodes in the network. On the other hand, in practical system the probability q1is small (i.e.,q1=0. 0607) and the event that more than twolinks countdown to zero at the same timeslot is of negligible probability (i.e.,=0. 0037).Observing this, to simplify the analysis we only consider the collision events of two links and the events that more than two links collide are not incorporated in the analysis.

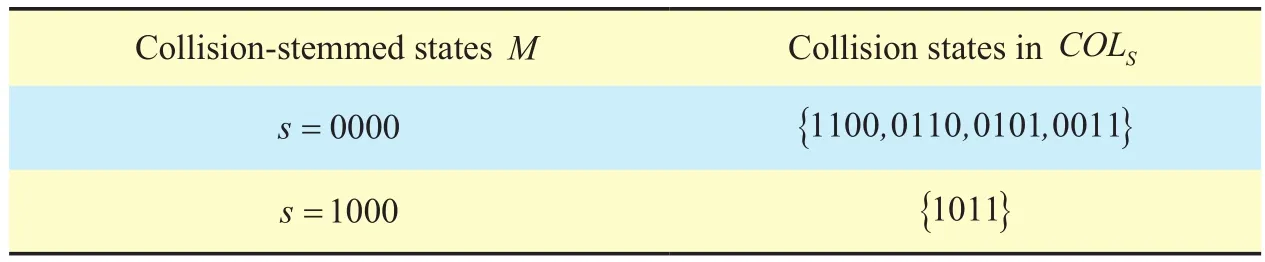
Table I. Collision-involved states of the network shown in figure 1.

3.2.2 Transition rates between states in EICN

We next compute the transition rate between states in GC. For each state s in M, we compute the transition rates to/from its neighbor states.

i). Transition Rates between states s andCOLs

To identify the transition rate from state s to COLs, rsCOLs, we first count the pairs of the neighbor links that are actively counting down in state s, which is equal to the number of collision states in COLs. Note that each pair of such neighbor links contribute a transition rate of q1λ from s to COLs. Thus, given that the collision probability of two actively counting-down links is q1, the transition rate from state s to COLsis

ii). Transition Rates between state s and its non-collided states

For each state s∈M, we separate its non-collided states into two subsets: the left neighbors Lsand the right neighbors Rs.

· For each s′∈ Rs, recall that s′ has one extra link that is transmitting compared to s, and denote this link by link i. Assuming that link i has niactively counting-down neighbors in state s, the transition rate from s to s′ is given by

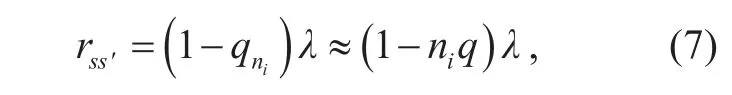
where qniis the collision probability of a link with niactively-countdown neighbors that can be computed by (4). We note that the approximation (1?qni)λ≈(1?niq) λ in (7) is only for quick computation. If more accurate analysis is required, we just use rss′=(1?qni)λ in computation. The transition rate from s′ to s is fixed to μ.

· Compared to s each state s′∈ Lshas one less link that is transmitting, the transition rate from s to s′ is fixed to μ , while the transition rate from s′ to s is determined by whether s′ is a collision-stemmed state. If s′? M, rλs′s=, otherwise, the transition rate from state s′ to state s is given by (7). Thus,we have

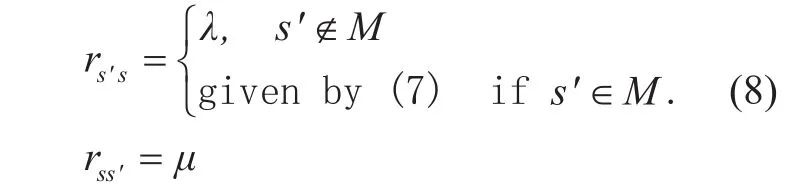
Excluding the collision states and the neighbors of the collision-stemmed states, we can easily fix the transition rates between the other states: the transition from a left state to a right state occurs at rate λ and the transition rate from a right state to a left state is μ.

In the network shown in figure 1, invoking(7) and (8), we have

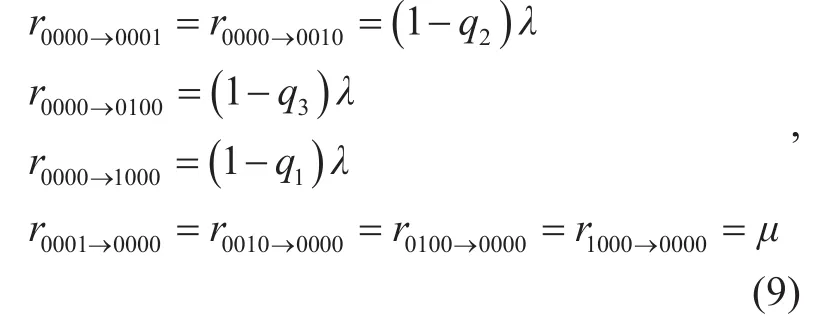
and

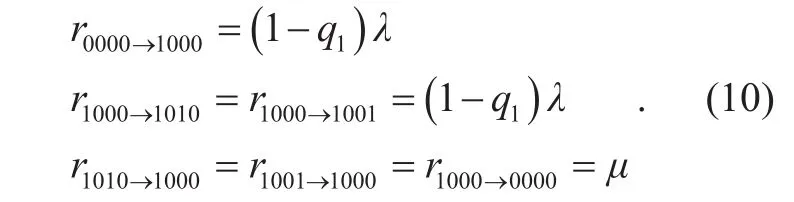
Thus far, we have constructed a complete collision-captured state-transition diagram under EICN model. For the network in figure 1,its collision-captured state-transition diagram with transition rates is presented in figure 2.Next we can compute the stationary probability of states, collision probabilities and throughputs of links.

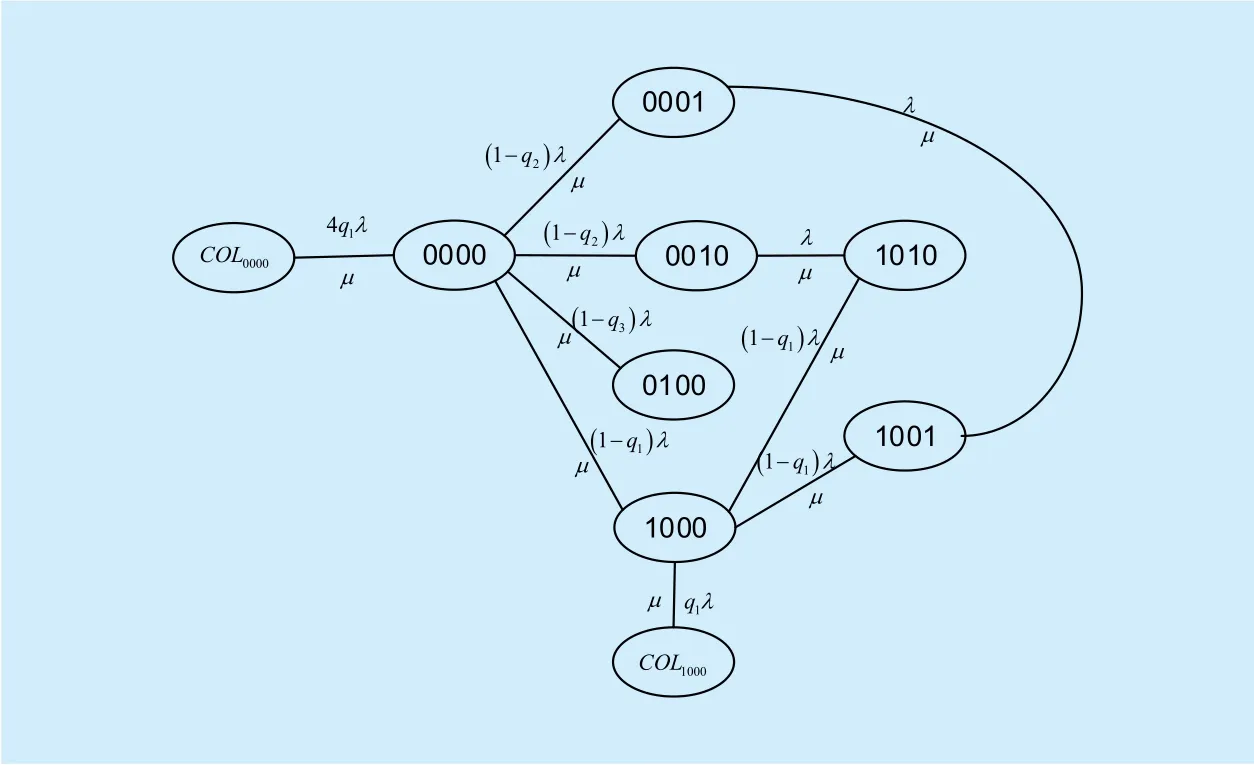
Fig. 2. The collision-involved state-transition diagram of the network shown in figure 1.

3.3 Link throughput computation under EICN

Assuming that the stationary probability of EICN has the product form as (1) in ICN,we next compute the stationary probability distribution of states in EICN. Based on this stationary distribution, we can compute:

i). links’ normalized throughputs

ii). the collision probability of each link(11) shown in the top at next page.

For the network in figure 1, we have (12)shown in the top at next page.and the collision probabilities

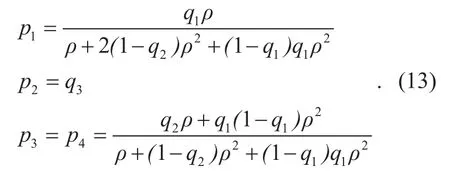
Given a typical value of ρ=83/ 15. 5 ,the normalized link throughputs and collision probabilities are

and

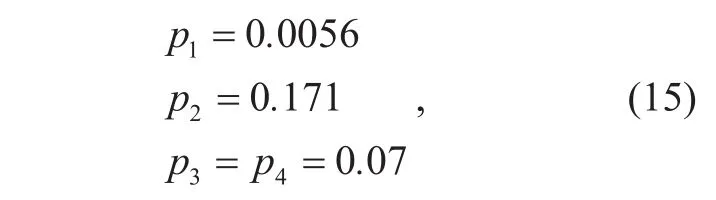
respectively. MATLAB simulations validated this result.

Remark 3: In the analysis we make the assumption that the stationary probabilities of EICN have the product form as (1). Indeed,we can prove that the system process of EICN is still time-reversible, which is a necessary condition for the stationary distribution to have the product form. In general, as stated in[17], the stationary probability distributions of many time-reversible non-Markovian stochastic processes have the product form. Unfortunately, we have not yet figured out a suf ficient condition for the stationary probability distributions of EICN to have the product-form.More mathematical proof was left for future work.

Remark 4: If we compute link throughputs using (1) and ρ=83/ 15. 5 without considering collision effects in CSMA wireless network, we have

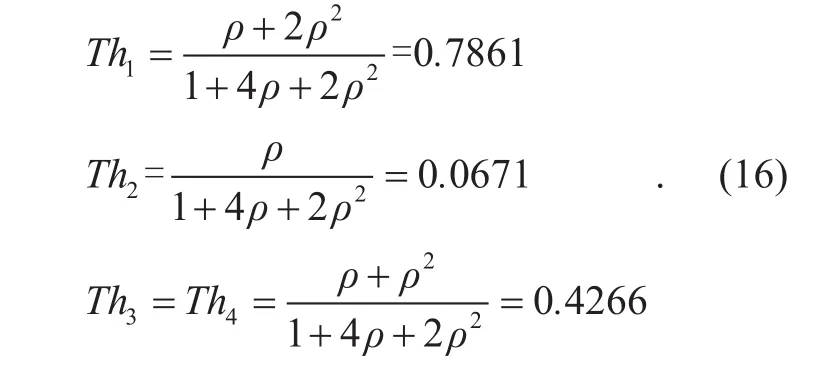
Compared (15) with (16), the link collision probabilities in the network can be rather high.For example, the collision probability of link 2 is 17.1% when link 2 has three neighbor links.However, we observe that although it could suffer from non-trivial collisions, the link throughputs do not vary largely (e.g., 0.0671 if we do not consider collisions and 0.0604 if collisions are taken into account).

Remark 5: Note that we consider IEEE 802.11 DCF Basic mode in this paper. Our treatment on DCF in the Basic mode can be easily extended to the RTS/CTS mode by updating the related parameters. Speci fically, in RTS/CTS mode, the packet transmission time is

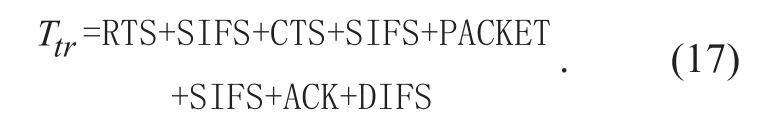
If a collision occurs, the collided transmission time becomes

When the IEEE 802.11 protocol is operated in RTS/CTS mode, we need to compute the packet transmission time and the collided transmission time using (17) and (18), respectively. The other procedures are the same as the Basic mode.

IV. SIMULATION EVALUATION

We next conduct simulations to verify the accuracy of EICN and examine the effects of collisions on link throughputs in CSMA networks. Specifically, besides NS2 simulations, we also implement the discrete-time CSMA protocol using MATLAB programs(i.e., a discrete-time CSMA simulator) to examine the interactions among links. The link throughputs computed by ICN and EICN are compared with that obtained from the discrete-time CSMA simulator as well as NS2 simulations. For EICN, we further compare the collision probabilities of links with that collected in simulation. For a typical IEEE 802.11b network, the contention window is 31 mini-timeslots (CW=31), and the packet transmission time is 83 mini-timeslot7The detailed mapping from IEEE 802.11 protocol and ICN model can be found in [2]..

Typical 802.11b and default NS2 parameters were used in the simulations: (i) data rate and basic rate of 11Mbps and 1 Mbps, respectively; (ii) we set carrier-sensing range to 550m; (iii) packet length of 1460 Bytes; (iv)for each UDP session, a CBR flow of 7Mbps was used to ensure link saturation. Finally,the link length was fixed to 200m for all links.Each simulation runs for 200 seconds.

We note that in our analysis, as shown in Assumption 1 of Section II-2.3, we assume that the contention window is NOT doubled upon collisions, which is not consistent with practical 802.11-like protocols. To justify this assumption, we perform the MATLAB simulations under two different protocol settings:simulations with window-doubling (WD) disabled and simulations with window-doubling enabled. The purpose is to evaluate whether Assumption 1 makes our analysis of EICN lose accuracy. Furthermore, to extensively examine the accuracy of EICN, we perform simulations under different network topologies and protocol parameter settings.

4.1 Speci fic network topologies

We first consider two sets of speci fic network topologies in figure 3 and figure 4, where the first column is the tested network topology,the second and the third column list the link throughputs and the collision probabilities computed by ICN and EICN, respectively. The fourth and the fifth columns list the simulated link throughputs and the collision probabilities collected from the CSMA simulator without or with the window-doubling mechanism, respectively, and the sixth column lists the simulated results using NS2.

As can be seen from figure 3 where CW is set to 31, the normalized link throughputs and the link collision probabilities computed by EICN are very close to the simulations (especially for the case that the window-doubling mechanism is disabled) for all the topologies tested. Also, for all the topologies, EICN is more accurate than ICN, since ICN does not take packet collisions into account. In general,the normalized throughputs collected in NS2 are a bit smaller than those from MATLAB simulations, since more protocol details and overheads are involved under NS2 environment.

Second, unlike often expected, under typical protocol settings link throughputs do not change largely when collision effects are taken into account. That is, for a modest-size CSMA wireless network where each link has three to four neighbors, we could ignore the effects of collision events when computing link throughputs. Furthermore, figure 3 shows that when we disable the WD mechanism, the link collision probabilities are a bit higher. However,the link throughputs remain almost the same.

We next examine the accuracy of EICN by setting CW=7 so that packet collision occur with higher probability8We note that in IEEE 802.11a/b/g networks,the minimum contention window size is 15. Here we use an extreme value (i.e.,CW=7) to examine the accuracy of EICN under severe collisions.. Figure 4 shows the comparison between the normalized link throughputs and the link collision probabilities for the case CW=7. As can be seen, the packet collision probabilities largely increase in contrast to the case of CW=31. Even for the network with two connected links, the collision probability is up to 22.22%. In this case,the computation of ICN loses its accuracy in some topologies. However, the computation of EICN keeps high accuracy compared with the simulation results even when WD mechanism is enabled. Meanwhile, we note that although the collision probabilities in networks with and without WD mechanism are different, the normalized link throughputs do not vary much.Thus, our assumption of no window-doubling mechanism (Assumption 1) does not lose much accuracy as far as the link throughputs are concerned.

In addition to the simulations in figure 4,we also simulate the fully-connected clique network where all links can sense each other and each node has the same experience in channel competition. It is known that the clique network has the highest collision probabilities. Table 2 below shows the computed normalized link throughputs/collision probabilities of ICN/EICN, the simulated normal-ized link throughputs/collision probabilities both with/without WD mechanism. Since this is a symmetric network and each link has the same experience, we only list the throughput/collision probability of a single link in table 2.

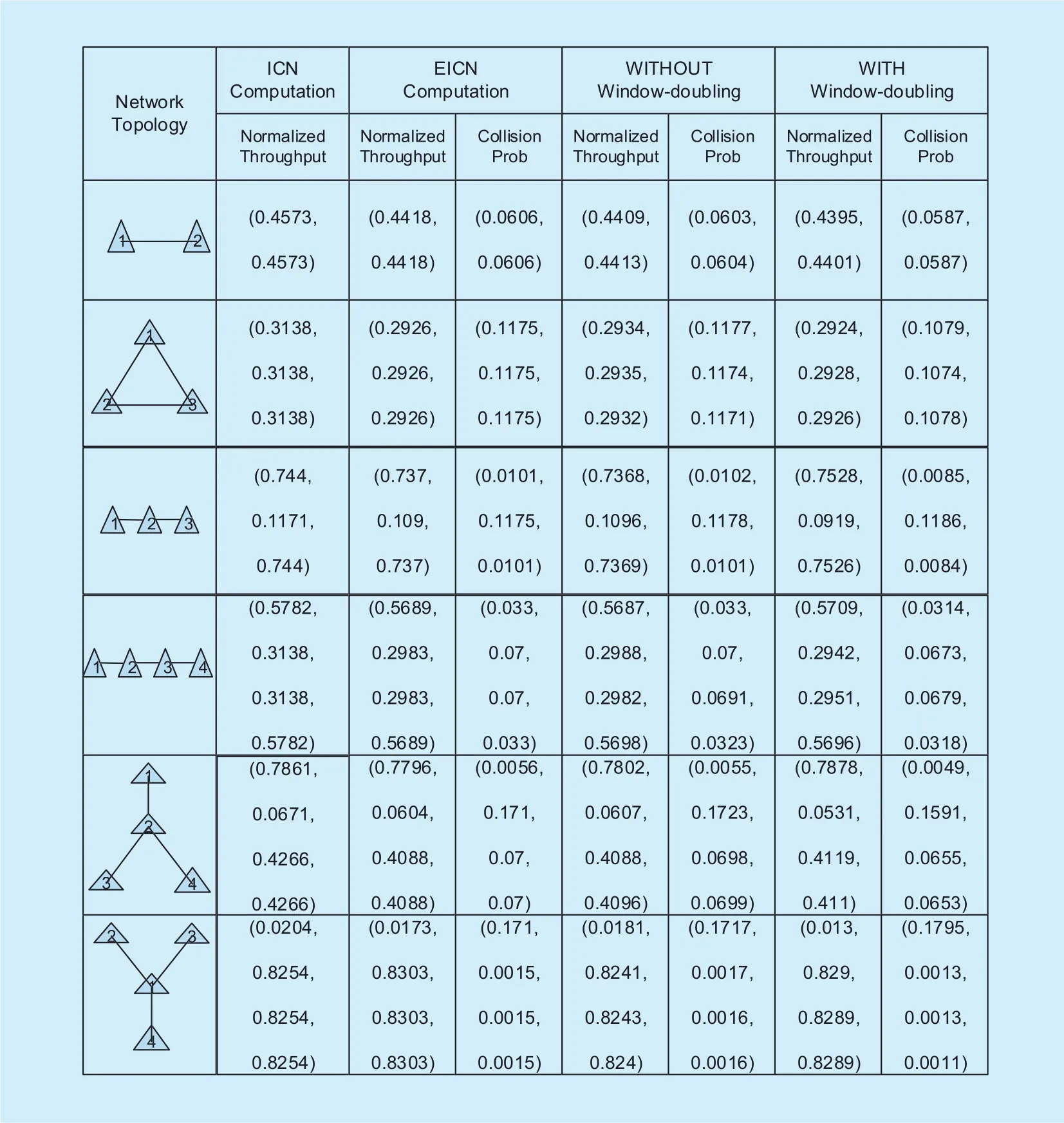
Fig. 3. Contention graphs of various network topologies and the corresponding ICN, EICN computed link throughputs/Collision probabilities simulation results (both with and without WD mechanism) where CW=31.

4.2 Random network topologies

For random networks, we run three sets of ten randomly generated 6-link networks.

Setting 1:we generate networks with different mean degree of links (i.e., the number of neighbors per link in the contention graph)to around two and three.

Setting 2:for the ten networks with mean link degree to two, we adjust the contention-window size.

Setting 3:for the ten networks with mean link degree to two and CW=31, we enable/disable the window-doubling mechanism.

For each network, we define the mean link throughput error to beand mean collision probability error to bewhere thiand pidenote the normalized throughput and the normalized collision probability of link i computed by EICN, while thi′ and pi′ denote the normalized throughput and the normalized collision probability of link i collected from the CSMA-simulator or NS2 simulation.

Fig. 4. Contention graphs of various topologies and the corresponding ICN, EICN computed throughputs/collision probabilities and simulation results (both with and without mechanism) where CW=7.

Table 3, 4, and 5 list the mean link throughput errors and the mean collision probability errors for the three simulation settings, respectively. In these tables, each datum is averaged over ten random networks. As can be seen, the normalized link throughputs and the link collision probabilities computed by EICN are very close to the simulated results obtained from the CSMA-simulator and NS2 simulation.

The mean link throughput error and the mean collision probability error of EICN are kept below 4% for all tested scenarios. To sum up,our EICN computation is of high accuracy.

Furthermore, we note that for all the scenarios tested, the WD mechanism does not signi ficantly improve the system performance.This is due to the fact that in a typical practical CSMA wireless network (i.e., a modest-size network in which a node has four to five neighbors), the link throughputs do not decrease much due to packet collisions incurred by two neighbor links’ counting-down to zeroat the same mini-timeslot and transmitting together. For example, as shown in the left column of table 3, the differences of simulated results between With/Without WD Mechanism is kept to 1% or below.

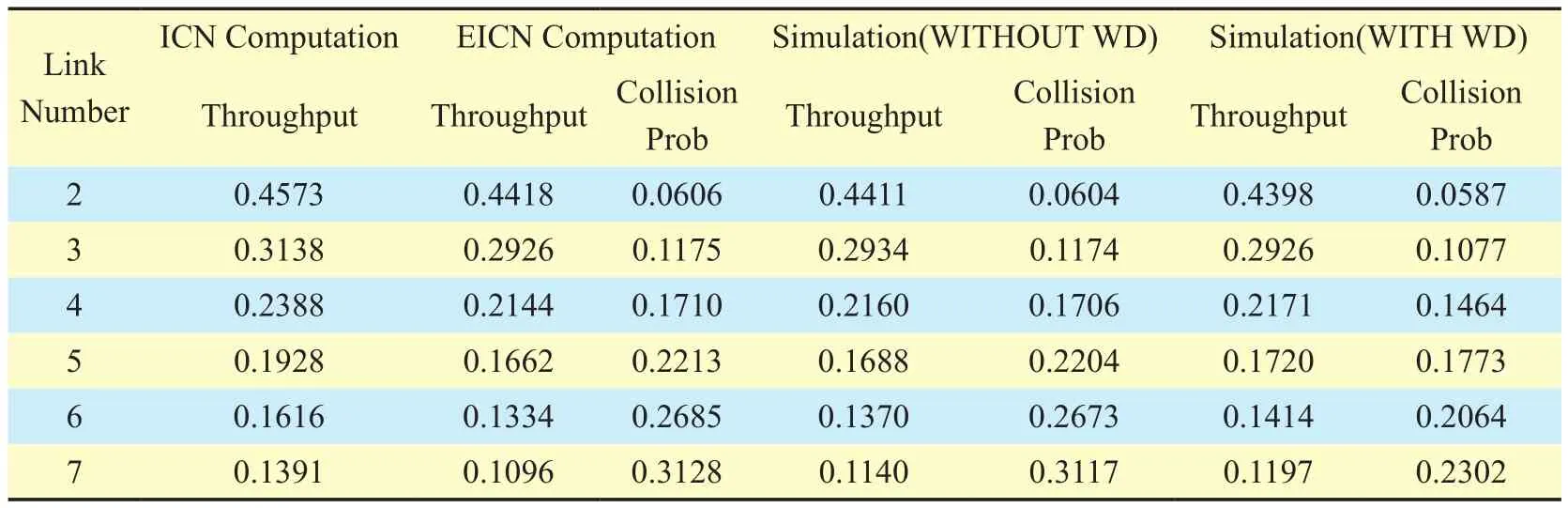
Table II. Mean normalized link throughput/collision probability of ICN and EICN for fully-connected networks.

V. CONCLUSION

This paper presented an EICN model to characterize the collision effects in CSMA wireless networks. By identifying the collision states and constructing a collision-captured state-transition diagram, we provide a method to compute the link throughputs and collision probabilities. Simulation results validate the accuracy of EICN computation. For various network scenarios tested, EICN is of higher accuracy than ICN, especially when the packet collision probabilities are high. Furthermore, the impacts of packet collisions on link throughputs are evaluated for various CSMA wireless networks. Therefore, this work can be considered as an important step towards the understanding on practical CSMA wirelessnetworks, such as Wi-Fi. For example, we find that unlike expected, the effect of collisions in a modest CSMA wireless network is not significant as far as the link throughputs are concerned. However, to keep mathematical traceability we also made some assumptions in the analysis, such as a fixed transmission time. The removal of such assumptions awaits further work.

Table III. Mean normalized link throughput/collision probability errors for networks with different mean link degrees (CW=31).

Table IV. Mean normalized link throughput/collision probability errors for networks with different contention windows (mean degree=2).

Table V. Mean normalized link throughput/collision probability errors for network with/without WD mechanism (CW=31, mean degree=2).

ACKNOWLEDGEMENT

This work was partially supported by the National Natural Science Foundation of China under Grant 61571178, Grant 61771315 and Grant 61501160.

[1] B. Bellalta, A. Zocca, C. Cano, A. Checco, J.Barcelo, and A. Vinel, “Throughput Analysis in CSMA/CA Networks Using Continuous Time Markov Networks: A Tutorial,” Wireless Networking for Moving Objects, Protocol, Architectures,Tools, Services and Applications. Springer, vol.8611, 2014, pp. 115-133.

[2] S. C. Liew, C. H. Kai, H. C. Leung, and P. Wong,“Back-of-the-Envelope Computation of Throughput Distributions in CSMA Wireless Networks,” IEEE Trans. on Mobile Computing,vol. 9, no. 9, Sep. 2010, pp. 1319-1331,

[3] R. Laufer and L. Kleinrock, “On the Capacity of Wireless CSMA/CA Multihop Networks,” Proc.IEEE INFOCOM, Apr. 2013, pp.1312-1320.

[4] IEEE Std 802.11-1999, IEEE 802.11 Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Speci fications.

[5] C. K. Chau, W. H. Ho, Z. Situ, S. C. liew, and J.Zhang, “Effective Static and Adaptive Carrier Sensing for Dense Wireless CSMA Networks,”IEEE/ACM Trans. Mobile Computing, vol. 16, no.2, 2017, pp. 355-366.

[6] G. Bianchi, “Performance Analysis of the IEEE 802.11 Distributed Coordination Function,” IEEE J. Selected Areas in Communications, vol. 18, no.3, March 2000, pp. 535-547.

[7] L. Jiang and J. Walrand. “Approaching Throughput-Optimality in Distributed CSMA Scheduling Algorithms With Collisions,” IEEE/ACM Trans. on Networking, vol. 19, no. 3, June 2011, pp. 816-829.

[8] S. P. Subrahmanya, G. R. Krishna, and J. Krishna,“Adaptive CSMA under the SINR model: efficient approximation algorithms for throughput and utility maximization,” IEEE/ACM Trans. On Networking, vol. 25, no. 4, 2017, pp. 1968-1981.

[9] M. H. Chen, S. C. Liew, Z. Y. Shao, and C. H. Kai,“Markov Approximation for Combinatorial Network Optimization,” IEEE Trans. on Information Theory, vol. 59, no. 10, 2013, pp. 6301-6327.

[10] C. H. Kai and S. C. Liew. “Temporal Starvation in CSMA Wireless Networks,” IEEE Trans. on Mobile Computing, vol. 14, no. 7, July 2015, pp. 1515-1529.

[11] S. Tang, L. Ma, and Y. Xu, “A novel AP placement algorithm based on user distribution for indoor WLAN system,” China Communications, vol. 13,no. 10, 2016, pp. 169-180.

[12] R. H. Hou, J. D. Li, M. Sheng, and C. G. Yang,“Access point selection in heterogeneous wireless networks using belief propagation,” Science China Information Sciences, vol. 57, no. 6, 2014,pp. 1-10.

[13] B. Bellalta, A. Checco, A. Zocca, and J. Barcelo,“On the Interactions between Multiple Overlapping WLANs Using Channel Bonding,” IEEE Trans. on Vehicular Technology, vol. 65, no. 2,2016, pp. 796–812.

[14] B. Nardelli and E. W. Knightly, “Closed-form throughput expressions for CSMA networks with collisions and hidden terminals,” Proc. IEEE INFOCOM, 2012, pp. 2309–2317.

[15] R. Diestel, “Graph Theory,” Oberwolfach Reports,vol. 311, no. 1, 2000, pp. 67-128.

[16] A. Kochut, A. Vasan, A. Shankar, and A. Agrawala. “Sniきng out the correct Physical Layer Capture model in 802.11b,” Proc. 12th IEEE Inter.Conf. on Network Protocols, Oct. 2004, pp. 252-261.

[17] F. P. Kelly. “Loss networks,” The Annals of Applied Probability, vol. 1, no. 3, 1991, pp. 319-378.