Community detection in multiplex networks via consensus matrix
Ning Nianwen, Wu Bin
?
Community detection in multiplex networks via consensus matrix
Ning Nianwen, Wu Bin
(Beijing University of Posts and Telecommunications, Beijing 100876, China)
In complex network of real world, there are many types of relationships between individuals, and the more effective research ways for this kind of network is to abstract these relationship as a multiplex network. More and more researchers are attracted to be engaged in multiplex network research. A novel framework of community detection of multiplex network based on consensus matrix was presented. Firstly, this framework merges the structure of multiplex network and the information of link between each node into monoplex network. Then, the community structure information of each layer network was obtained through consensus matrix, and the traditional community division algorithm was utilized to carry out community detection of combine networks. The experimental results show that the proposed algorithm can get better performance of community partition in the real network datasets.
multiplex network, community detection, consensus matrix
1 Introduction
Community structure is widely present in a variety of real-world networks including social, technology and computer science brain, biological networks and technological systems. Community is a set of nodes with dense connections among themselves, and with only sparse connections to other communities in a network[1]. The relationship of community members are generally admitted to share common proprieties, it can give us many insights about the overall structure of the network by mining this relationships in complex system and network. Community detection is a process that finds an underlying community structure in complex networks and has attracted signi?cant attention during the past several years. Several methods has been proposed to address the problem of community detection in multiplex network. However, a most of literature only have focused on analyzing simple static networks, where all edges are of the same type. Real networks often are heterogeneous, dynamic and multi-relational that actors in a group are tied together by various types of relationships[2,3]. The concept of multiplex network has been introduced in order to ease modeling such networks. For example, the multiple of relationships in social network can be abstracted as multilayer network comprised of multiple interdependent networks, where each network represents an aspect. Multiplex networks are a special type of multilayer network where contains same set of nodes but nodes cannot be interconnected with other nodes in other layers, don’t consist of layer couplings[4].
Multiplex network mining is often used for social network analysis. Fig.1 shows an example of an undirected multiplex network. Graph G is an example consists of 7 nodes participating in three layers. If we analyze each layer separately, each layer has the same number of nodes and different number of edges. The essence of forming edges between the nodes in each layer is not the same. This network can represent a different relationship between the same nodes in different scenarios of real-world, such as: 1) a set of friendship between users in heterogeneous information networks, e.g. Facebook, Twitter and LinkedIn[5], 2) a set of different types of online and offline relationships between the same of employees in the daily life, e.g. Leisure, Work, Lunch[6]. Aim at to detect community in multiplex network exposes several challenges. How to exploit and fuse the multiple aspects of information to enhance the performance of community detection algorithms. How to consider the topology information of each layer network to detect community is an important open question. A large number of theory and approaches on community detection have been proposed for monoplex network(i.e., single-type links or single property). But these concepts and methods need to be redefined in a multiplex network.
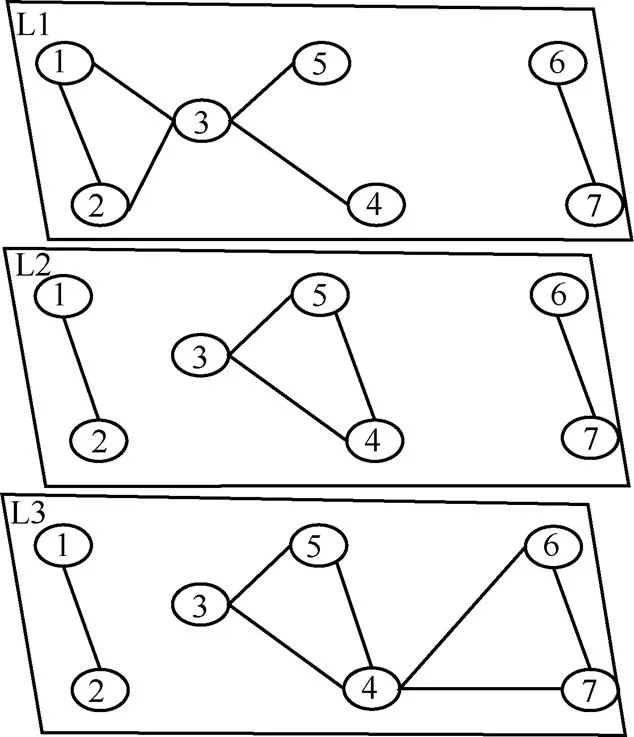
Fig. 1 Graph G is an example consists of 7 nodes
In this paper, we address the problem of community detection in multiplex networks inspired by literature[7] to fuse information of the multiple layers. The paper is organized and our contributions are as follows. In section II, we introduce brief literature review of multiplex community detection theory, methods and mains notations used later in this paper. In section III, we present in details of our approaches including the theory, layer aggregation function, consensus matrix, formulations and algorithm flows in multiplex network. Section IV presents comparison of four kinds community detection approaches and analyze the experimental results in multiplex networks. Section V summarizes our results.
2 Related works
2.1 Multiplex network
Multiplex network have proved to be a useful tool to model structural complexity of a variety of complex systems in different domains including sociology, biology, ethology and computer science. A multiplex network is represented by a graph={,,} in whichis set of nodes,is set of edges andis a set of layers, each member of which is a different type of links, andconsists of triples(,,) with,∈and∈. Each layer contains the same set of nodes but interconnected by different types of links. This visual extension of the basic graph model is powerful enough, and it allows modeling different types of networks including Ref.[8,9]. 1) Multi-relational network: where each layer encodes one relation type. 2) Dynamic network: where a layer corresponds to network state at a given time stamp, where the order of layers encode the arrow of time. 3) Attributed network: where additional layers can be de?ned over the node set as a similarity graph induced by a similarity measure applied to the set of node’s attributes.
In the recently research, aim at to rede?ne most of the basic concepts and metrics usually used for complex network analysis including: node’s degree[10]and centralities[11,12], the influence of layers[12], neighborhood[10,13], community structure. In this paper, we mainly focus on the Multi-relational network of research. The structure of Multi-relational network not allows for layers to be connected and ordered by inter-layer. Therefore, how to detect community from the Multi-relational network was regard as a challenge.
2.2 Community detection
In the monoplex networks, a huge number of community detection algorithms and theories are proposed. However, many types of connections may reside between any two nodes in real networks. Note that individuals often have multiple accounts across different social networks, as well as relations of different types can be available for the same population of a network. Traditional community detection and based monoplex network methods are no longer applicable to the current situation. Nevertheless, studying about monoplex network seems to be a better practice to complement our analyses of community discovery concept and methods. Thence, the most of solutions to the problem of multiplex network community detection is based on classical approach. The main solution strategy is as follows.
2.2.1 Based monoplex network approach
The research on monoplex network provides a well-grounded for solving the problem. Typically, this frame that solve to detect community in multiplex via classical method mainly has the following two steps.
1) Flatten the network into composite network
This operation consists on applying aggregation function to transform the multiplex into a monoplex network. A simple aggregation functionftransform a graph
consist of two weighted networks layerL= (V,E,W) andL=(V,E,W) into a composite graph={,,}.
={:∈(V∪V)},
= {(,): (,)∈(E∪E),,∈},
={:w+w=w, (,, w)∈E, (,, w)∈E) }
The result of applying the function to the network in Fig.1 is shown in Fig.2. The literature [14] proposed a 3-uniform hyper-graph to map multiplex network. Given the network adjacency matrix of-th layer is[k], a hyper-graph={V,E},V=V∪1,…,, (,,)∈Eif ?:A,v≠0,,∈,∈1,…,. The method based on quantum theory to reduce the number of layers to a minimum was proposed by Ref.[15]. Although, the performance was implemented by maximizing the distinguishability between the multilayer network and the corresponding aggregated graph, transportation systems can be reduced by up to 75%, rather than forming a monoplex network.
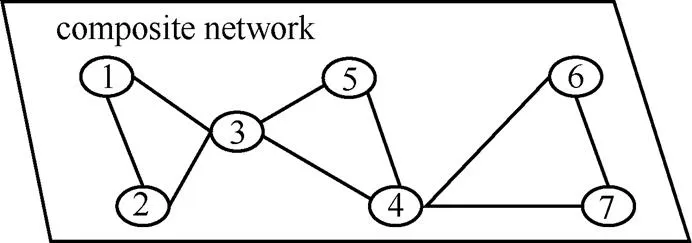
Fig.2 A aggregation function f transform into a composite graph
2) Classical community detection in composite network
We have acquired composite network from the last step, and can use classical method to detect community based on this network, e.g. Spectral clustering algorithm, Graph partition Hierarchical clustering, Louvain method, Modularity maximization method, Label propagation method and so on.
The use of aggregation will result in the loss of information in the network. The Ref.[16] refers to the community partition that identified by many multiplex community detection approaches, which is best ?ts all given layers, i.e. The community of these method detection is shared by all layers. But some communities may be shared only by a subset of layers are ignored. In this paper, we also take into account the problem in the process of community division, so introduce the consensus cluster algorithm to store community information of each layer.
2.2.2 Extending monoplex approaches
There are few ways to simultaneously detect community in multiplex network. The Ref.[17] developed a generalized framework of network quality functions that allowed us to study the community structure of arbitrary multislice networks, which are combined of individual networks coupled through links that connect each node in one network slice to itself in other slices.
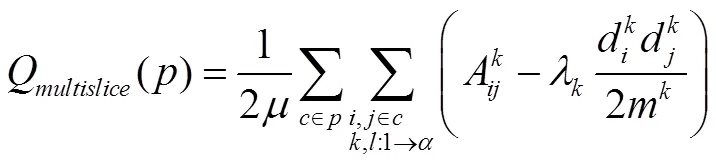
2.3 Definitions and Notations
The Multiplex networks: definitions and notations are shown in Table 1.
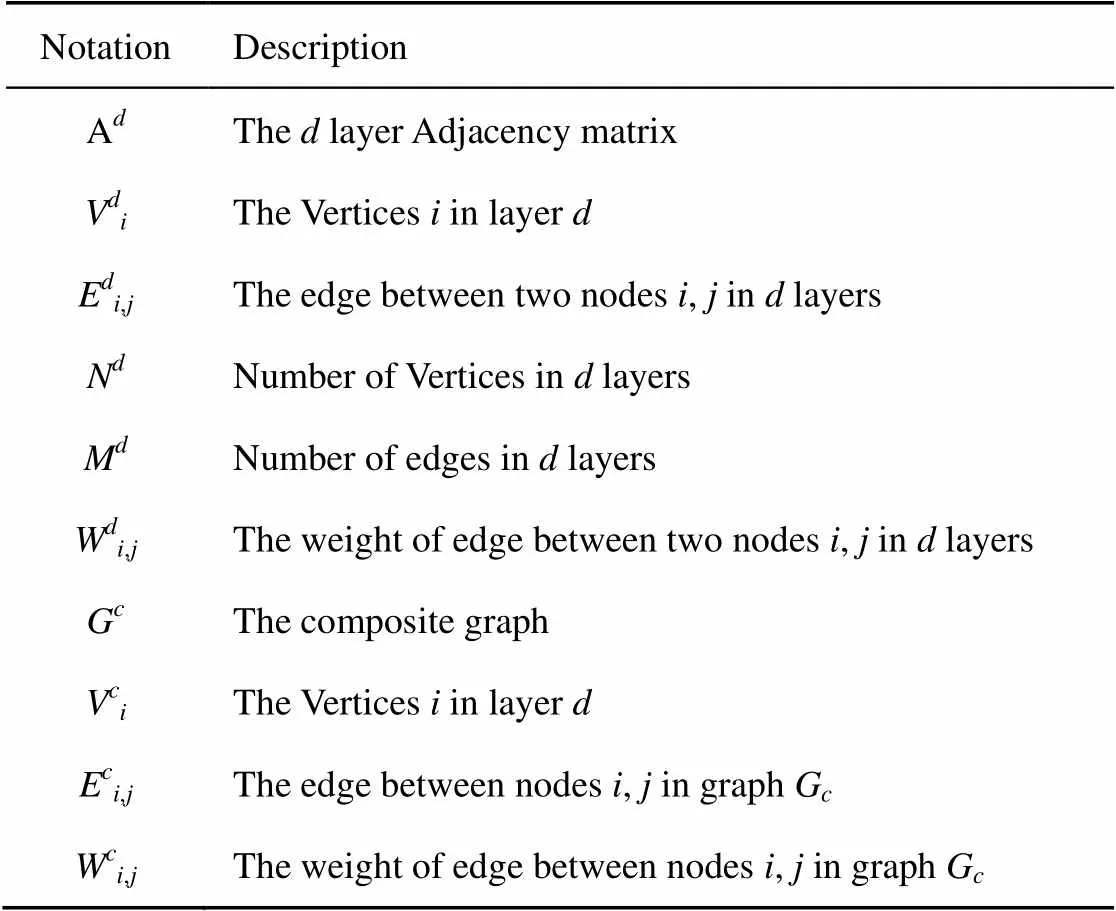
Table1 Multiplex networks: notations
2.4 Multiplex networks datasets
In this paper, we will validate and compare the performance of the algorithm in seven multiplex networks datasets, Details are as follows.
The EU-air transportation multiplex network is composed by thirty-seven different layers each one corresponding to a different airline operating in Europe. Nodes represent airports, while links stand for direct flights between two airports. On the other hand, each commercial airline corresponds to a different layer, containing all the connections operated by the same company.
The CS-Aarhus multiplex social network consists of five kinds of online and offline relationships (Facebook, Leisure, Work, Co-authorship, Lunch) between the employees of Computer Science department at Aarhus. These variables cover different types of relations between the actors based on their interactions. All relations are dichotomous which means that they are either present or absent, without weights.
The Kapferer tailor shop multiplex network present that interactions in a tailor shop in Zambia (then Northern Rhodesia) over a period of ten months. Layers represent two different types of interaction, recorded at two different times (seven months apart) over a period of one month. TI1 and TI2 record the "instrumental" (work and assistance-related) interactions at the two times, TS1 and TS2 the “sociational” (friendship, socioemotional) interactions. The data are particularly interesting since an abortive strike occurred after the first set of observations, and a successful strike took place after the second.
The Lazega law firm multiplex network consists of 3 kinds of (Co-work, Friendship and Advice) between partners and associates of a corporate law partnership. The symmetrized collaboration relation was used between the 36 partners in the firm, where a tie is defined to be present if both partners indicate that they collaborate with the other.
The London multiplex network transport network was collected in 2013 from the official website of Transport for London and manually cross-checked Nodes are train stations in London and edges encode existing routes between stations. Underground, Overground and DLR stations are considered. The multiplex network used in the paper makes use of three layers corresponding to: 1) The aggregation to a single weighted graph of the networks of stations corresponding to each underground line (e.g., District, Circle). 2) The network of stations connected by Overground. 3) The network of stations connected by DLR. Raw data and geographical coordinates of stations are provided. We also provide the multiplex networks after considering real disruptions occurring in London.
The Pedgett Florentine Families multiplex network consists of 2 layers (marriage alliances and business relationships) describing florentine families in the Renaissance. The particular one we chose describes the marital relations among 16 most prominent Florentine families in the 15th century. Each family is a node and two families are connected if there is a marriage between them. The two included attributes are “wealth”, which is measured in thousands of lira and indicates economic power, and “priorates”, which is the number of seats held in the civil council and indicates political power.
The Pierre Auger multiplex network consists of layers corresponding to different working tasks within the Pierre Auger Collaboration. We considered all submissions between 2010 and 2012 and assigned each report to 16 layers according to its keywords and its content, with manual disambiguation to avoid spurious results from an automated process. The multiplex network used in the paper makes use of 16 layers corresponding to: Neutrinos, Detector, Enhancements, Anisotropy, Pointsource, Mass-composition, Horizontal, Hybrid-reconstruction, Spectrum, Photons, Atmospheric, SD-reconstruction, Hadronic-interactions, Exotics, Magnetic, Astrophysical-scenarios.
3 Community detection
In this section, we present a community detection frame-work via consensus matrix(CDCM),and consider that the loss of information, especially community structure information when the multiplex network is transformed into a composite network, eventually leads to the obvious community structure and the incorrect community structure in the composite network. Therefore, the existent information of edge between the same nodes and community structure information of each layer to retaining the multiplex network structure. We treat the number of edges formed between the same nodes as the information of edge in each layer. In order to achieve to retain community structure information when network merging, the consensus matrix algorithm which integrates the community information into consensus matrix and then acts on composite network is applied. Finally, Louvain method based on modularity maximization to calculate and tests community structure in the multiplex network and the composite network.
3.1 Generate composite network
We propose simple layer aggregation function that flattens the multiplex network into a composite network and retain the edge information of multiplex network. In this way edges formed between the same nodes in each layer is transformed into the edge weight information in the final composite network. The edge weight information reflects the situation of link between the nodes in multiplex network, the detailed process is showed as Algorithm 1.
Input:{L, L,, L}
Output:Monoplex network G = {V , E , W }
():
G = {V , E , W }
For
If VV
V ={V , V}denote VinlayerputedintoV ;
EndIf
EndFor
For,1(V )
0;
For1
If E ,jisexist
If E ,j E,j
E,j{E ,j, E,j}denotethe V, Varelinked;
EndIf
;
EndIf
EndFor
W,j;
EndFor
Return the composite graph G
EndFunction
Algorithm 1 implements the transformation between multiplex network with monoplex network and here weightrepresents the occurrences of connections among pairs of nodes . On the basis of the generated composite network, a more accurate discovery of the community structure and other operations can be realized. The result of applying the algorithm to the graph G in Fig.1 is shown in Fig.3. The composite graph consists of all nodes and edges of graph G. The= {[(1, 2), 3]}, [(1,3),1], [(2,3),1],[(3,5),3],[(3,4),3],[(4,5),2],[(4,6),1],[(4,7),1],[(6,7),1]}. [(1,2),3] indicates that the edges formed between the nodes 1 and 2 are present in the 3 layers. Hence, the result graph reflects the situation the link between the nodes of multiplex graph.
3.2 Consensus Clustering
We present an effective method fusing community structure information of multiplex via consensus matrix. When the multiplex network is transformed into a composite network, the loss of information, especially for community structure information, leads to community structure is non-obvious even wrong community partition in the composite network. As to the community structure in different layers, we use consensus clustering for acquiring and fusing community structure information. Consensus clustering is a well-known technique used in data analysis to solve this problem. Typically, the goal is to search for the so-called median (or consensus) partition, i.e. the partition that is most similar, on average, to all the input partitions. Consensus matrix can preserve and integrate various community partition information.
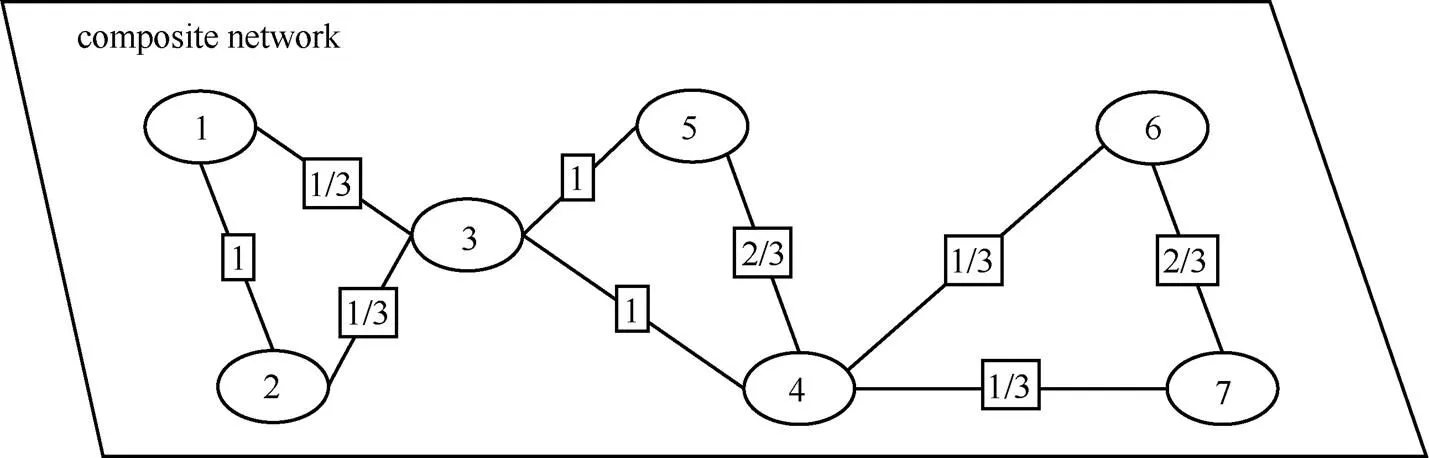
Fig.3 Alg.1 transform a graph G in Fig.1 into a composite graph
In the monoplex network, such as modularity maximization algorithm, label propagation algorithm and so on, the partition result of network is always unstable because of many algorithms are random. A consensus clustering algorithm based on consensus matrix was proposed by Ref.[7]. The algorithm integrates multiple partitioned community structures, which enhances correct community partition and weakens the division and misclassification caused by randomness. Among them, consensus matrix bases on the co-occurrence of vertices in clusters of the input partitions. The consensus matrix is an input for the graph clustering technique adopted, leading to a new set of partitions, which will generate a new consensus matrix, etc. until a terminate condition is finally reached. This process of algorithm can quickly achieve a stable and higher quality of community partition. The link-prediction enhances consensus clustering for complex networks proposed in Ref.[20]. The prediction performance of algorithm improved by this method. In this paper, we use consensus matrix to retain the community structure information of multiplex network, the process of calculating the consensus matrix is as Algorithm 2.
The starting point is a networkwith n vertices and a clustering algorithm. Applyontimes to yieldpartitions,{1,2,…, L}. Computing the consensus matrix, whereDis the number of partitions in which verticesandofare assigned to the same cluster, divided by.
Input:{1,2,…, P},Monoplex network G
Output:Combine network G = {V , E , W }
(, G):
G =G
For1
’(P)denote communitydetectionofgraph PusingAlgorithm,withtheresult’;
EndFor
For,1(V )
0;
For1
If,j∈,jand,aresamecommunityCount;
EndIf
EndFor
W ,j= W ,j();
EndFor
Return the composite graphG
EndFunction
3.3 The community detection algorithm via consensus matrix
The framework of community detection via consensus clustering based on the formation of composite network in the previous section. The main idea of the method as follows:
Firstly, the community structure of each layer is obtained by some method, and the consensus matrix is formed by the community partition of each layer. This step mainly uses the consensus matrix to retain the community structure information of the multiplex network.
Secondly, the multiplex network merges into a composite network using the method of Alg.1, and the weight of edges in the composite network are calculated by the consensus matrix, and the fusion network is obtained. The method is mainly to make the fusion network, which has the multiplex network community structure information;
Finally, some method detects the community structure in the fusion network.
The method of community detection is, such as, consensus clustering, Louvain method, or other. The pseudocode and processing steps of the CDCM framework shows as follows.
Input:{1,2,, L}
Output:Community network G = {V, E, W}
():
G = Function GenerateFunction()
G = Combinefunction(, G)
G = f(G)
EndFunction
4 Experimental Results
In order to verify the performance of CDCM framework for multiplex network community, we propose a multiplex network community detection algorithm based on Louvain algorithm. We use the modularity in Equation 1 and seven kinds of recognized multiplex network datasets as the evaluation metric of the algorithm performance, whereλ= 1. The algorithm of comparative multi-layer network community is used in this paper is as follows.
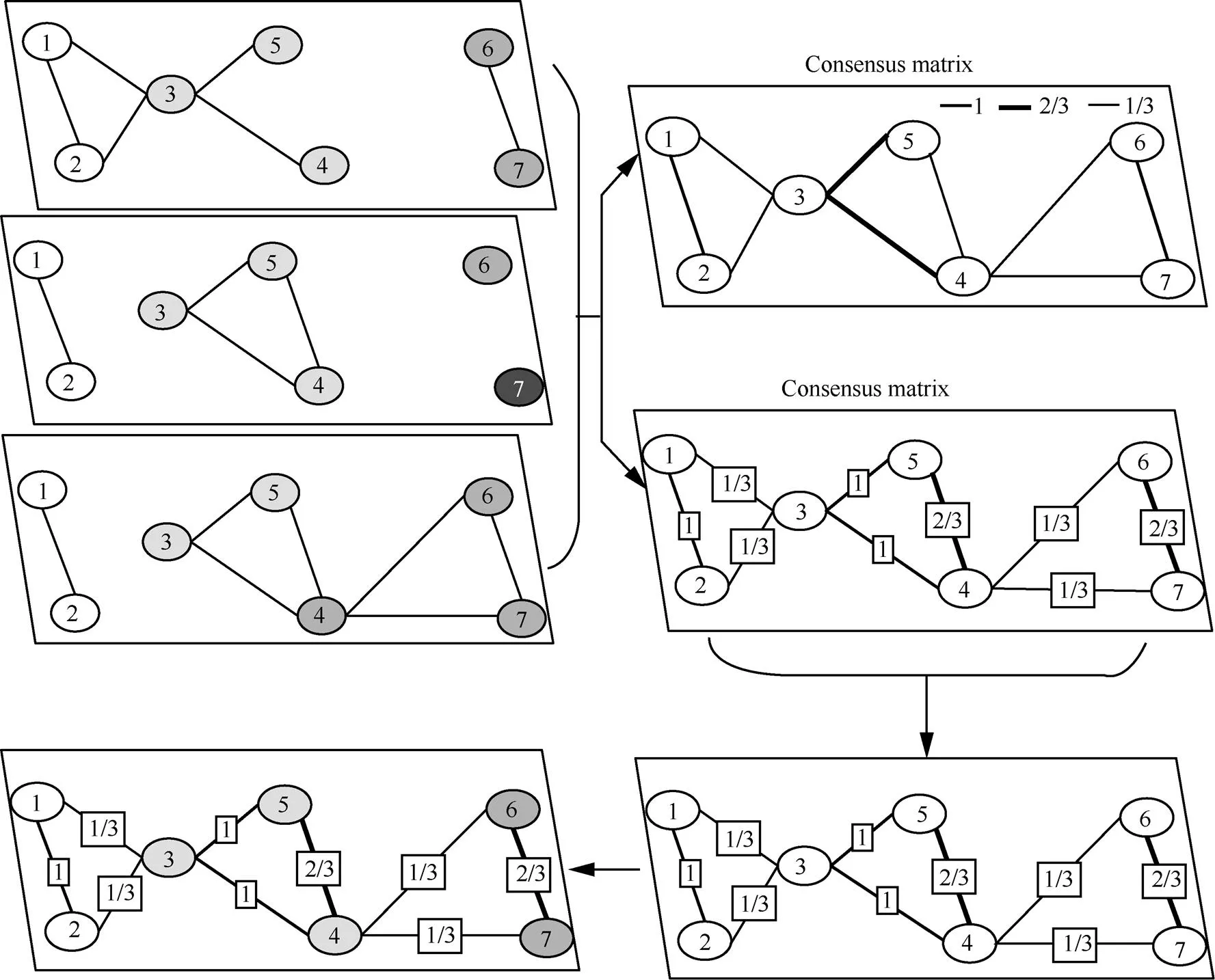
Fig.4 Our Framework Diagram
GenLouvain[21]is a very convenient generalized Louvain community discovery package for monoplex and multilayers networks. This package consists of the main genlouvain.m file which calls a number of subroutines implemented as mex functions. It includes iterated_genlouvain.m which iteratively applies genlouvain on the output partition of the previous run with optional post-processing. Functions to compute modularity matrices and to post-process partitions are included in the “HelperFunctions” directory with functions togenerate different types of monolayer and multilayer modularity matrices.
MoIti, a standalone user-friendly graphical software. MoIti detects communities from multiplex networks provided by the users, by optimizing the multiplex modularity with the adapted Louvain algorithm. MolTi further optionally performs Fisher tests of annotation enrichment for the detected communities, and allows an easy exploration of the results.
Platten algorithm merge a simple multiplex network as a monoplex composite network by the process shown in Alg.1, thus the community detection in the network by Louvain method. Then, we utilize multiplex modularity matrices to measure the performance of the algorithm. Due to the method is only plain and violent flattened multiplex network, and did not take into account other network attributes, it will lead to network distortion.
Fig.5 and Fig.6 illustrate the CDCM algorithm to perform better than the GenLouvain, MoIti, and Platten. These algorithms are executed 10 times on 7 kind of recognized multiplex datasets. However, the CDCM algorithm does not perform well in the EU dataset, with poor modularity values compare to GendLouvain and Molti. After a detailed analysis, we find that the EU dataset is an unweighted multiplex network dataset, thus we set the weighted value of all edges to 1. Between each layer of the network only has few overlapping edges, the network community structure is not obvious after flattened and the final modularity values is poor. Simultaneously, because the combine network retains a certain amount of multiplex network of community structure information, so it is able to meet the requirements of the community, which is, the modularity is greater than 0. In general, the algorithms we propose have better performance in multiplex network community division and are within reasonable limits.

Fig.5 The comparing modularity of the result
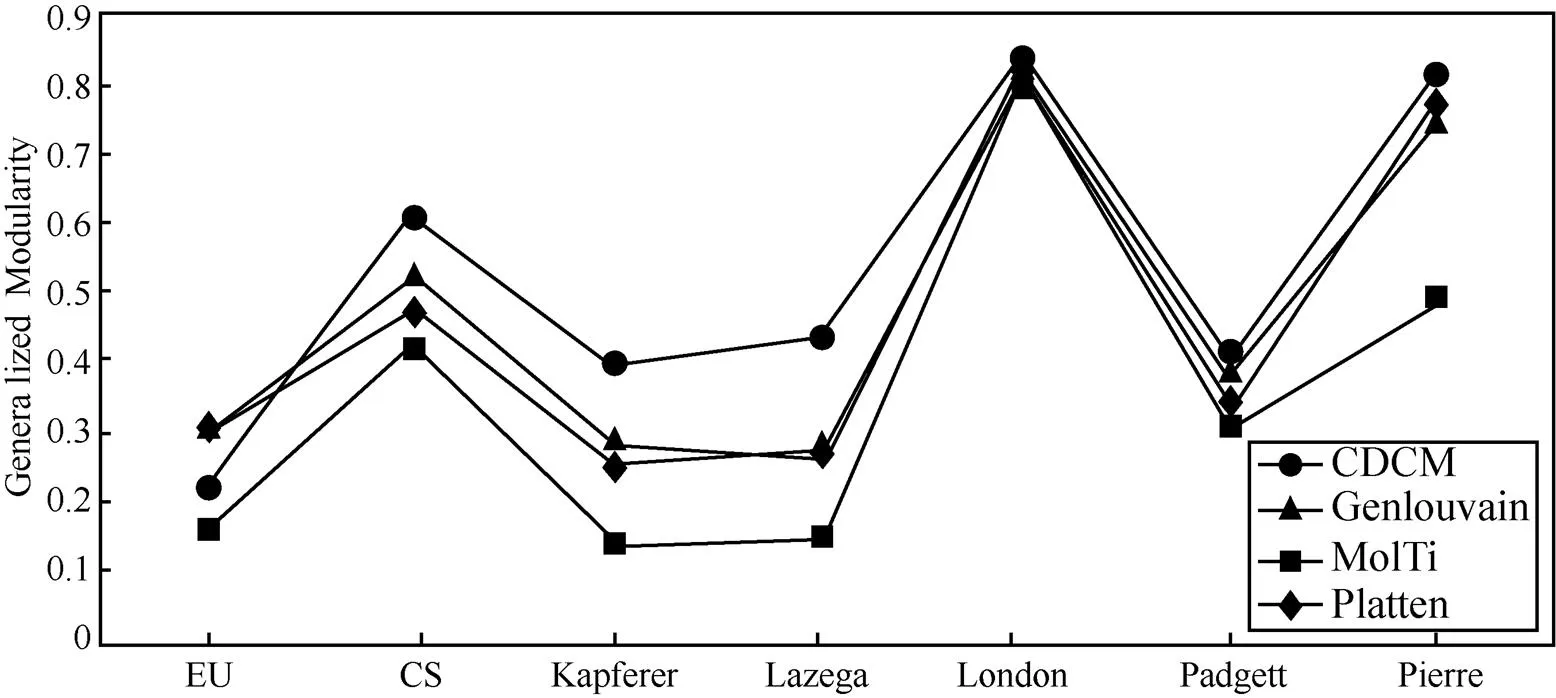
Fig.6 Compare the average modularity size for each dataset
Platten method obtains better structure than GenLouvain in the London dataset, with similar performance in both the Lazega law firm multiplex and the Pierre Auger multiplex data set. Therefore, the composite network obtains by alg.1 can reflect the real link situation between the nodes of real-world multiplex network. In most data sets, in addition to EU-air transportation multiplex, it can be intuitively understood that the CDCM algorithm is superior to the Platten method. This reflects the fact method of preserving the community structure information of the multiplex network through consensus clustering is very effective and is beneficial to detecting community structure of the multiplex network.
5 Conclusion
This paper first analyzes the detection of the current multiplex network community, and presents a community detection framework based on consensus matrix. By comparing with frequently-used community detection methods and software, it is clear understand that by preserving the situation that the link between the two nodes in each layer and the community structure information of each layer, and integrating this information into a monoplex network that transformed from multiplex network, it can improve the effectiveness and accuracy of using of this monoplex network for detecting community. At the same time, this paper also puts forward an attempt: As a result, there are many mining methods in the monoplex network, how to use this advantage to mine the multiplex network? The attributes of the multiplex network are extracted first, then merged into the monoplex network, and finally action about that attribute is executed. Through the final experimental results we can notice that this attempt is effective and feasible.
[1] SARZYNSKA M, LEICHT E A, CHOWELL G, et al. Null models for community detection in spatially embedded, temporal networks[J]. Biorxiv, 2014(3).
[2] FALIH I, KANAWATI R. MUNA: a multiplex network analysis library[C]//IEEE/ACM International Conference, ACM. 2015: 757-760.
[3] CARDILLO A, ZANIN M, ROMANCE M, et al. Emergence of network features from multiplexity[J]. Scientific Reports, 2013, 3(2):1344.
[4] KIVEL? M, ARENAS A, BARTHELEMY M, et al. Multilayer networks[J]. Ssrn Electronic Journal, 2013, 2(3):261 - 268.
[5] LAMBIOTTE R. Multirelational Organization of Large-scale social networks in an online world[M]// PNAS. 2010.
[6] CARDILLO A, ZANIN M, ROMANCE M, et al. Emergence of network features from multiplexity[J]. Scientific Reports, 2013, 3(2):1344.
[7] LANCICHINETTI A, FORTUNATO S. Consensus clustering in complex networks[J]. Scientific Reports, 2012, 2(13):336.
[8] KANAWATI R. Multiplex network mining: a brief survey[J]. IEEE Intelligent Informatics Bulletin, 2015, 16: 24-28.
[9] CARCHIOLO V, LONGHEU A, MALGERI M, et al. Communities unfolding in multislice networks[J]. Communications in Computer & Information Science, 2011, 116:187-195.
[10] BATTISTON F, NICOSIA V, LATORA V. Metrics for the analysis of multiplex networks[J]. 2013, 89:032804.
[11] ALHAJJ R, ROKNE J. Encyclopedia of social network analysis and mining[M]. Springer Publishing Company, Incorporated, 2014.
[12] RAHMEDE C, IACOVACCI J, ARENAS A, et al. Centralities of nodes and influences of layers in large multiplex networks[J]. arXiv preprint arXiv:1703.05833, 2017.
[13] KAZIENKO P, BRODKA P, MUSIAL K. Individual neighbourhood exploration in complex multi-layered social network[C]//Web Intelligence and Intelligent Agent Technology (WI-IAT), 2010 IEEE/WIC/ACM International Conference on. IEEE, 2010, 3: 5-8.
[14] COMAR P M, TAN P N, JAIN A K. Simultaneous classification and community detection on heterogeneous network data[J]. Data Mining and Knowledge Discovery, 2012, 25(3):420-449.
[15] DE D M, NICOSIA V, ARENAS A, et al. Structural reducibility of multilayer networks[J]. Nature Communications, 2015, 6:6864.
[16] KUNCHEVA Z, MONTANA G. Community detection in multiplex networks using locally adaptive random walks[C]//IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. ACM, 2015:1308-1315.
[17] MUCHA P J, RICHARDSON T, MACON K, et al. Community structure in time-dependent, multiscale, and multiplex networks[J]. Science, 2010, 328(5980):876.
[18] CARCHIOLO V, LONGHEU A, MALGERI M, et al. Communities unfolding in multislice networks[J]. Communications in Computer & Information Science, 2011, 116:187-195.
[19] KANAWATI R. Community detection in social networks: the power of ensemble methods[C]// ACM/IEEE International conference on data science & advanced analytics. ACM, 2014:46-52.
[20] BURGESS M, ADAR E, CAFARELLA M J, et al. Link-prediction enhanced consensus clustering for complex networks[J]. PLOS ONE, 2015, 11(5).
[21] JUTLA I S, JEUB L G S, MUCHA P J. (2011–2012) A generalized Louvain method for community detection implemented in MATLAB[EB/OL]. http://netwiki.amath.unc.edu/GenLouvain/ GenLouvain.
[22] DIDIER G, BRUN C, BAUDOT A. Identifying communities from multiplex biological networks[J]. Peerj, 2015, 3(7307): e1525.
10.11959/j.issn.2096-109x.2017.00199
2017-07-10.
2017-08-03.
Ning Nianwen, nianwenning@bupt.edu.cn
The National Key Basic Research and Department Program of China (No.2013CB329606)
NingNianwen(1991-), born in ZhouKou. He is working on his Ph.D. degree at Beijing University of Posts and Telecommunications. His research interests include social network analysis and machine learning.

Wu Bin(1969-), born in Hunan. He received his Ph.D degree of institute of computing Chinese academy of sciences in 2002. He is a professor in Beijing univer- sity of posts and telecommunications. His research interests include complex net- work, data mining, massive data parallel processing, visual analysis and telecom customer relationship management.

