Some new observations for a stage-structured predator-prey model
Li Wei,LiXianyi(Departmentof Big Data Science,College of Science,Zhejiang University of Science and Technology,Hangzhou 310023, China)
Some new observations for a stage-structured predator-prey model
Li Wei,LiXianyi?
(Departmentof Big Data Science,College of Science,Zhejiang University of Science and Technology,Hangzhou 310023, China)
A 3D stage–structured predator–prey model,whose necessary and sufficient conditions for the permanenceoftwo speciesand the extinction ofone speciesortwo specieswere previously obtained, is revisited in this paper.By using the centermanifold theorem,we show thatthe nonnegative equilibrium pointof this system is also locally asymptotically stable in the criticalcase a=b+ce.Our main new discovery is thatthe parameter d in this modelirrelevantto finite dynamicalbehaviors ofthis system plays a role in the dynamicalbehaviors atinfinity ofthis system.More specially,by using the Poincar′e compactication in R3we make a globalanalysis for this model,including the complete description of its dynamic behavior on the sphere atinfinity.Combining analyticaland numericaltechniques we show that for the parameters satisfying a≤b and 0<d<1,the system presents two infinite heteroclinic orbits.
stage–structured predator–prey model;centermanifold theorem;dynamics atinfinity; Poincar′e compactification;infinite heteroclinic orbit
2010 MSC:34C45,34C37,34D20


1 Introduction
Itis known to allthatthe predator–prey models have been extensively studied by many researchers[1?10]in recentyears,whose permanence(orstrong persistence)and extinction are importantcontentsofinvestigations.Almost allanimals have the stage structure ofimmature and mature in realbiologicalworld.So the related models with stage structure are more closely aligned with the objective facts.Recently,those papers[11?13]studied the stage structure of species with or withouttime delays.Mostof them considered the finite behaviors for those models.However,the dynamicalbehaviors atinfinity of those models are notknown atall.One has now seen thatthe dynamics atinfinity of a given modelis an interesting and importanttopic[14?20],especially with the biologicalmeanings of a biological system.Therefore,in this paper,our step goes on toward this orientation-the dynamics atinfinity of a given model.
Our main work is to make a globalanalysis forthe following stage-structured predator–prey model

which is presented in[21],and where the parameters(a,b,c,d,e)∈R+5are all positive realnumbers due to their biologicalmeanings.
Although the authors in[21]did notgive the detailed conditions for the existence of equilibrium of system(1), one can easily derive the following proposition.
Proposition 1 Forthe parameters(a,b,c,d,e)∈R+5,system(1)has always the equilibrium point O(0,0,0). Furthermore,one has:
(1)If a≤b,then the origin O is the unique equilibrium pointofsystem(1);
(2)If b<a≤b+ce,then system(1)has two equilibria.Namely,besides the origin O there is a non-negativeequilibrium E
(3)If a>b+ce,then system(1)has three equilibria,i.e.,exceptthe origin O and the non-negative equilibriumE1,there is also a positive equilibrium
Some dynamics of three equilibria have been considered in[21]and the localdynamics of the three equilibria are firstpresented.For the non-negative equilibrium E1,the resultis:
Result 1[21]is a saddle with dim Wu(E1)=1,dim Ws(E1)=2 for a>b+ce;E1is globally asymptotically stable for b<a<b+ce.
How aboutthe local stability of equilibrium E1in the criticalcase a=b+ce?This has notbeen answered yetin the known literature.So,in the sequel,we willfirstsolve this problem by using the center manifold theorem. Although the globalstability of equilibrium E1in the criticalcase a=b+ce is solved by using Lyapunov function and LaSalle theorem,our method is differentfrom the one used in[21].So,our method may be also regarded as a complementary method.
For the globaldynamics of the three equilibria,some results are obtained as follows.
Result 2[21]If a>b+ce,then the positive equilibrium E2of system(1)is globally asymptotically stable. If b<a<b+ce,then the non-negative equilibrium E1of system(1)is globally asymptotically stable.If a≤b, then the origin O of system(1)is globally asymptotically stable.
The numericalsimulations performed also confirm these theoreticalresults,for example,see Fig.1.

Figure 1 Phase portraitofsystem(1)with the same initialvalue(x0,y0,z0)=(2.618,1.382,0.382)and the parameters satisfying:(a)a>b+ce,(b)b<a≤b+ce,(c)a≤b
By carefulobservations,one finds that,the above Result2 forthe globaldynamicsofsystem(1)is only related to its parameters a,b,c and e,notthe parameter d.Thatis to say,the parameter d has nothing to do with the global stability ofthis system.Then,whatrole does the parameter d play in the dynamics of system(1)?Because system (1)is derived from a realbiologicalmodelby a dimensionless change,the parameter d,if returned to its original system,corresponds to some biologicalfactors.Since itis related to biologicalfactors,itmustaffectsomething of the population.Therefore,a naturalquestionˋˋHas system(1)been explored thoroughly?′′comesoutin ourmind.It seems thatthe answeris notobvious.Butone can easily find thatResult2 is only concerned with its finite dynamical behaviors.Thatis to say,its dynamics at infinity has notbeen investigated yet.So,one naturally conjectures:The parameter d effects the behaviors at infinity of system(1).Indeed,it is proved in the sequel that the conjecture is true.
The system(1)can be extended to an analytic system on a closed ballof radius one,whose interior is diffeomorphic to R3and whose invariantboundary,by the extended flow,is a 2-dimensionalsphere S2and playsthe role of the infinity.The technique formaking such an extension is precisely the Poincare′ compactification and is described in detailin Section 3.Itwillbe used here forstudying the dynamics ofsystem(1)in a neighborhood ofinfinity and on the sphere atinfinity.
Our main results in this paper are summarized in the following two theorems.
Theorem 1 For the parameters(a,b,c,d,e)∈R+5,for the infinite equilibria at coordinate axes of system (1),we have the following conclusions:
1.The two equilibria in the positive and negative endpoints ofthe x–axis are two unstable nodes.
2.The two equilibria in the positive and negative endpoints ofthe y–axis are two centers.
Furthermore,the following statements hold:
(i)If 0<d<1,the two equilibria in the positive and negative endpoints of the z–axis are two saddle–nodes, there stillare infinitely many saddle–node points with a 1Dand a 2Drespectively.
(ii)If d≥1,the two non-hyperbolic equilibria in the positive and negative endpoints of the z–axis are all unstable with a 1Dand a 2D,too.
For the phase portraitof system(1)on the sphere atinfinity,see Fig.2.

Figure 2 Phase portraitof system(1)atinfinity
Theorem 2 For the parameters satisfying 0<d<1 and a≤b,system(1)has two infinite heteroclinic orbits;one consists of the origin,the positive portion of the z–axis and of one equilibrium on the sphere atinfinity (the endpointof the positive z–axis),and the other consists of the origin,the negative part of the z–axis and one equilibrium on the sphere atinfinity(the endpointofthe negative z–axis),See Fig.3.

Figure 3 Infinite heteroclinic orbits of system(1)for 0<d<1 and a≤b(The boundary ofthe disks corresponds to the points atinfinity in the y–z plane,see Fig.2.)
The restof this paper is organized as follows:in Section 2,we show thatequilibrium E1is locally stable in the criticalcase a=b+ce.In Section 3 we presentthe Poincar′e compactification for a polynomialvector field in R3which will allow us in Section 4 to provide a complete description of system(1)dynamics at infinity and partially near infinity.From the results stated in the fourth section it follows statements of Theorems 1–2.A conclusion is drawn in Section 5.
2 Localstability of equilibrium E1in the criticalcase a=b+ce
For the localstability of equilibrium E1in the criticalcase a=b+ce,one has the following results.
Theorem 3 The equilibrium E1ofthe system(1)is locally asymptotically stable in the criticalcase a=b+ce.
Proof In the criticalcase a=b+ce,E1reduces to E1(e,e,0).Take the change x1=x?e,x2=y?e,x3= z?0,which transforms the system(1)into
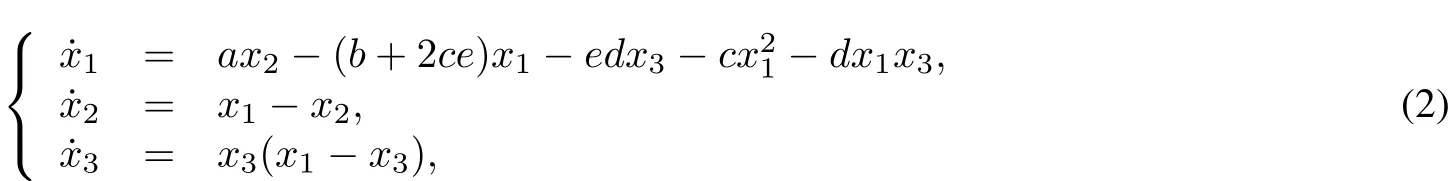
and E1to the origin O.The corresponding Jacobian matrix is
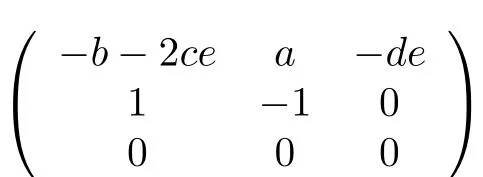
with an eigenvalue 0.So,O is then a center.According to the center manifold theory,the stability of O can be determined by studying a first-orderordinary differentialequation on a centermanifold,which can be represented as a graph for the variable x3as follows
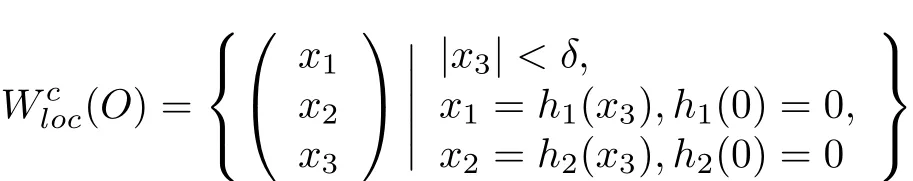

Hence,the vectorfield is reduced to the centermanifold

By the known assumption c>0 and d>0,itfollows from(3)that x3→0 for t→+∞.Thus,(x1x2,x3)in the system(2)tends to(0,0,0)when t→+∞.This imples thatthe origin O ofthe system(2)is asymptotically stable and thus the equilibrium E1ofthe system(1)is locally asymptotically stable.
3 Poincar′e compactification in R3
A polynomial vector field X in Rncan be extended to a unique analytic vector field on the sphere Sn.The technique for making such an extension is called the Poincar′e compactification and allows us to study a polynomial vector field in a neighborhood of infinity,which corresponds to the equator Sn?1of the sphere Sn.Poincar′e introduced this compactification for polynomialvector fields in R2.Its extension to Rnfor n>2 can be found in[20]. We here describe the Poincar′e compactification for polynomialvector fields in R3following closely[20].
In R3we consider the polynomialdifferentialsystem
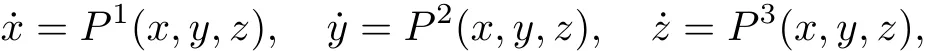
or equivalently its associated polynomial vector field X=(P1,P2,P3).The degree n of X is defined as n= max{deg(Pi):i=1,2,3}.
Let S3={y=(y1,y2,y3,y4)∈R4:‖y‖=1}be the unit sphere in R4,and S+={y∈S3:y4>0}and S?={y∈S3:y4<0}be the northern and southern hemispheres of S3,respectively.The tangentspace to S3at the point y is denoted by TyS3.Then the tangentplane
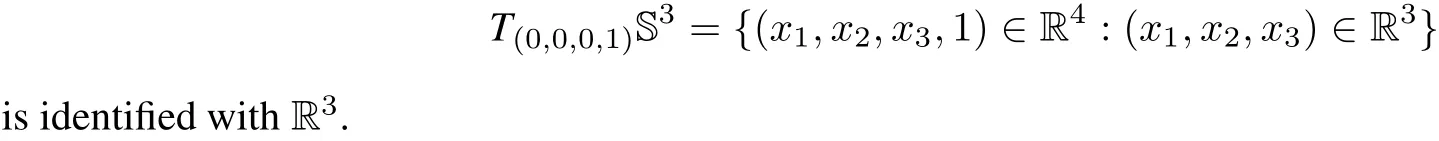
We considerthe centralprojections f+:R3=T(0,0,0,1)S3→S+and f?:R3=T(0,0,0,1)S3→S?defined by f±(x)=±(x1,x2,x3,1)/Δx,whereΔx=(1+Σ3i=1x2i)12.Through these centralprojections R3is identified with the northern and southern hemispheres.The equatorof S3is S2={y∈S3:y4=0}.Clearly S2can be identified with the infinity of R3.
The maps f+and f?define two copiesof X on S3,one Df+?X in the northern hemisphere and the other Df??X in the southern one.Denote byXˉthe vectorfield on S3S2=S+∪S?,which,restricted to S+coincideswith Df+?X and restricted to S?coincides with Df??X.
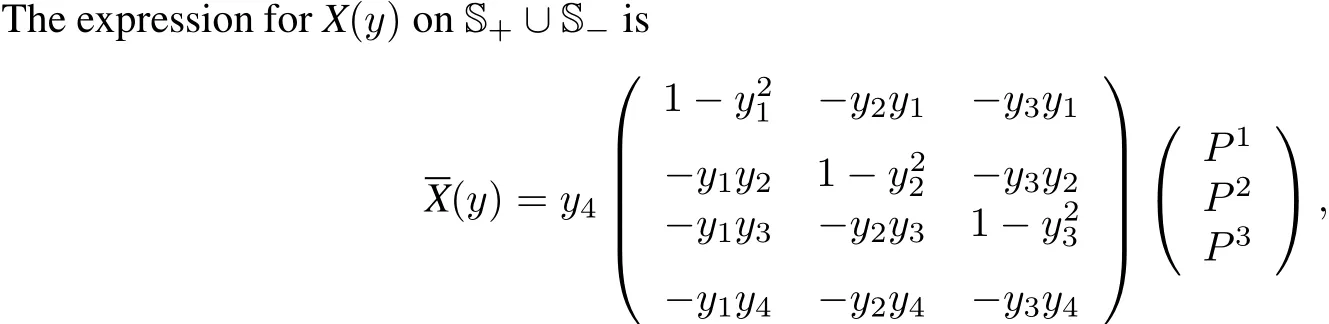
where Pi=Pi(y1/|y4|,y2/|y4|,y3/|y4|).Written in this way X(y)is a vector field in R4tangentto the sphere S3.
Now we can analytically extend the vector field X(y)to the whole sphere S3by considering p(X)(y) =,where n is the degree of X.This extended vector field p(X)is called the Poincare′ compactification of X on R3.
As S3is a differentiable manifold,in order to compute the expression for p(X)we can consider the eightlocal charts(Ui,Fi),(Vi,Gi),where Ui={y∈S3:yi>0}and Vi={y∈S3:yi<0}for i=1,2,3,4 are the inverses of the centralprojections from the origin to the tangent planes at the points(±1,0,0,0),(0,±1,0,0), (0,0,±1,0)and(0,0,0,±1),respectively.Now we do the computations on U1.Suppose thatthe origin(0,0,0,0), the point(y1,y2,y3,y4)∈S3and the point(1,z1,z2,z3)in the tangentplane to S3at(1,0,0,0)are collinear.Then we have 1/y1=z1/y2=z2/y3=z3/y4,and consequently F1(y)=(y2/y1,y3/y1,y4/y1)=(z1,z2,z3)defines the coordinateson U1.As■■

where Pi=Pi(z1/z3,1/z3,z2/z3)in U2,and
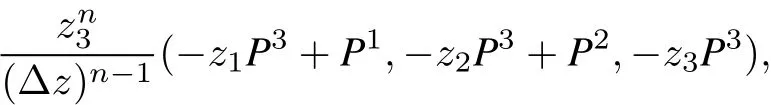
where Pi=Pi(z1/z3,z2/z3,1/z3)in U3.
The expression for p(X)in U4is(P1,P2,P3)where Pi=Pi(z1,z2,z3).The expression for p(X)in the localchart Viis the same as in Uimultiplied by(?1)n?1.
When we work with the expression ofthe compactified vectorfield p(X)in the localcharts we shallomitthe factor1/(Δz)n?1.We can do thatthrough a rescaling ofthe time variable.
Nextwe shallwork with the orthogonalprojection of p(X)from the closed northern hemisphere to y4=0,and we continue denoting this projected vectorfield by p(X).Note thatthe projection of the closed northern hemisphere is a closed ball B of radius one,whose interior is diffeomorphic to R3and whose boundary S2corresponds to the infinity of R3.Of course p(X)is defined in the whole closed ball B in such a way that the flow on the boundary is invariant.This new vector field on B will be called the Poincar′e compactification of X,and B will be called the Poincar′e ball.
Remark 1 Allthe points on the invariantsphere S2atinfinity in the coordinatesofany localchart Uiand Vihave z3=0.Also,the points in the interiorof the Poincar′e ball,which is diffeomorphic to R3,are given in the local charts U1,U2and U3by z3>0 and in the localcharts V1,V2and V3by z3<0.
4 Dynamicalbehaviorof system(1)atinfinity
In this section,we shallmake an analysis of the flow of system(1)near and atinfinity.
This section is divided into three subsections:in Subsection 4.1 we study the dynamics of system(1)near infinity;in Subsection 4.2,we consider the dynamics of system(1)atinfinity and consequently prove Theorem 1. Based on the knowledge ofthe dynamicalbehaviornearand atinfinity,in Subsection 4.3 we prove Theorem 2.
4.1 Dynamicalbehavior of system(1)near infinity
In this subsection we shallanalyze the flow ofsystem(1)nearand atinfinity.In orderto do so,in the following three subsections,we shall analyze the Poincar′e compactification of system(1)in the local charts Uiand Vi, i=1,2,3.
4.1.1 In the localcharts U1and V1
According to the method in Section 3,the expression of the Poincar′e compactification p(X)of system(1)in the localchart U1is given by
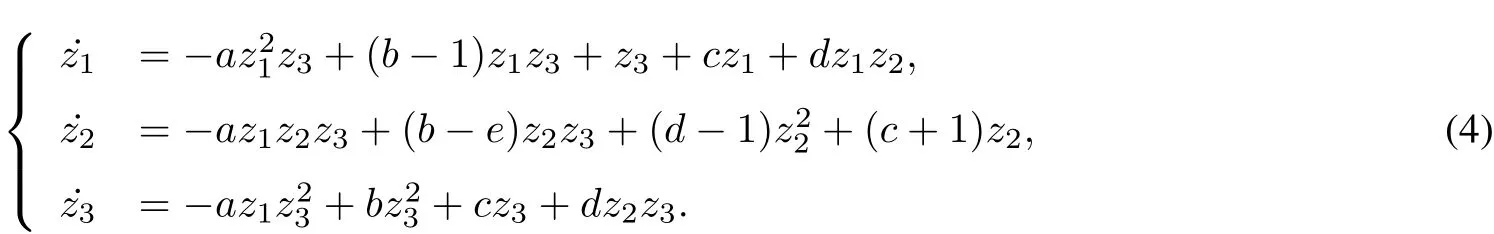
Taking z3=0(which correspondsto the pointson the sphere S2atinfinity),system(4)is reduced to the system as follows

Since d>0,we may considertwo cases:(i)d=1,(ii)d/=1.
(i)If d=1,then system(4)has a unique equilibrium point I0(0,0,0),and the corresponding three eigenvalues areλ1,3=c andλ2=c+1.Hence,I0is an unstable node because c>0.
(ii)If d/=1,thenis the other equilibrium point of system(4)in addition to I0.The three eigenvalues ofthe linearpartofsystem(4)at I areλ=andλ=?(c+1).Therefore,one can see that11,32I1is a saddle-node for 0<d<1,and a stable node for d>1.
The flow in the localchart V1is the same as the flow in the localchart U1,because the compactified vectorfield p(X)in V1coincides with the vector field p(X)in U1multiplied by(?1)n?1,where n=2 is the degree of system (1)(for details see Section 3).Therefore,the above analysis holds forthe flow in the localchart V1.
4.1.2 In the localcharts U2and V2
Again using the method in Section 3 we have the expression ofthe Poincare′ compactification p(X)of system (4)in the localchart U2as follows
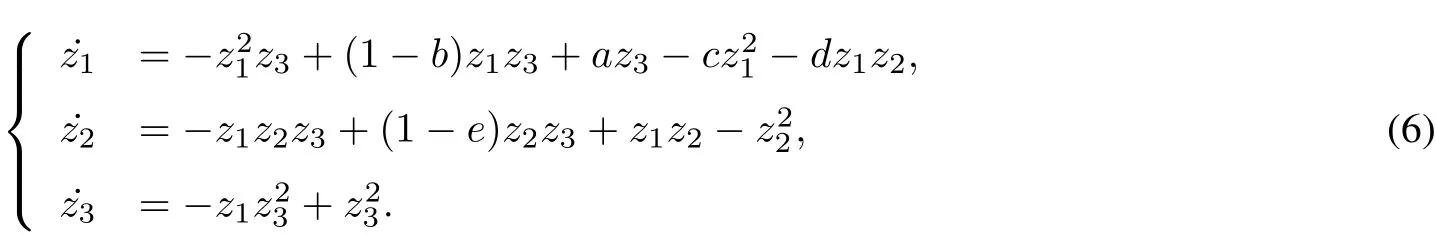
Notice z3=0 implies thatsystem(6)has a unique equilibrium point I0with three nulleigenvalues.Letus try to understand the flow near the equilibrium.From the compactification procedure described in Section 3 we know that the z1z2–plane is invariant under the flow of system(6),so we can completely describe the dynamics on the sphere atinfinity.In fact,for z3=0 system(6)restricted to the z1z2–plane is given by

The following resultmay be derived.
Proposition 2 The unique equilibrium point(0,0)of system(7)is stable.
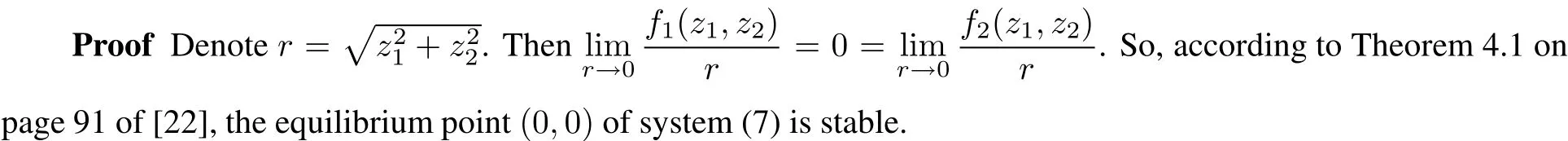
The flow in the localchart V2is exactly the same as the flow in the localchart U2,because the compactified vectorfield p(X)in V2coincideswith the vectorfield p(X)in U2multiplied by(?1)n?1,where n=2 is the degree of system(1).
4.1.3 In the localcharts U3and V3
The expression of the Poincare′ compactification p(X)of system(1)in the localchart U3has the form
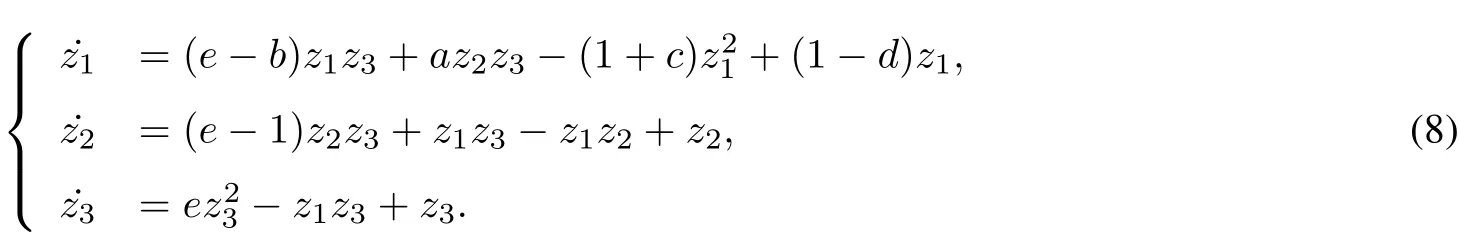
For z3=0,system(8)becomes the following system

Similar to the case for U1in 4.1.1,we consider two cases:(i)d=1,(ii)d/=1.
(i)If d=1,then I0is a unique equilibrium pointof system(8)with three eigenvaluesλ1=0 andλ2,3=1.So I0is a non-hyperbolic equilibrium pointwith a 1Dand a 2D.Further,itremains to analyze the dynamics of system(8)for z3>0 smallin the 1Drelated to I0.This is done in the nextproposition.
Proposition 3 When d=1,I0is stable along its 1D.
Proof Itfollows fromλ1=0 thatsystem(8)associated to the singular point I0has a 1D center manifold.Itis the graph of a function h:R→R2given by(z2,z3)=h(z1)=(h1(z1),h2(z1))satisfying the conditions

where we have used(10).The use of the condition(11)and the expressions for˙z1and˙z2in system(8)produces ai=bi=0 for all i≥2,i.e.,
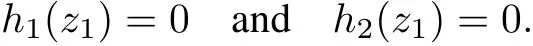
And so the flow on this manifold is governed by the equationz˙1=?(1+c)which implies that I0is locally stable along its center manifold because z1>0 in the localchart U3and c>0.
(ii)If d/=1,is the other equilibrium point of system(8)except I0.Its corresponding three eigenvalues areλ=d?1 andλ=Therefore,I is a saddle-node if 0<d<1,whereas itis an unstable
12,32node if d>1.Atthis time,the eigenvalues associated I0areλ1=1?d andλ2,3=1.So I0is a saddle-node if d>1,butan unstable node if0<d<1.
The flow in the localchart V3is the same as the flow in the localchart U3by reversing the time.So by the same type of analysis as stated above,using z3<0 near the infinity in the local chart V3(see Remark 1),we get the same result.
4.2 Dynamics of system(1)on the sphere at infinity
Putting together the analysis formulated in the previous subsections one has a globalpicture of the dynamical behavior of system(1)on the sphere at infinity.The system(1)has two unstable node in the positive and negative endpoints of the x–axis and two unstable centers with 1Dand 2Din the positive and negative endpoints of the y–axis.Further,when 0<d<1,system(1)has two equilibria in the positive and negative endpoints of the z–axis,which are two saddle–nodes;there are also infinitely many saddle–node points with a 1Dand a 2Drespectively;when d≥1,system(1)has the two non-hyperbolic equilibria in the positive and negative endpoints of the z–axis,both unstable with a 1Dand a 2D,See Fig.1.This displays Theorem 1.
We observe thatthe description ofthe complete phase portraitofsystem(1)on the sphere atinfinity is possible because ofthe invariance ofthis setunderthe flow ofthe compactifield system.
4.3 Infinite heteroclinic orbit
For a≤b and 0<d<1,the complex dynamicalbehavior of O(0,0,0)has been discussed in[21].It is easy to check thatthe z–axis is invariantunder the flow of system(1),and itfollows from the calculations above thatthe origin is asymptotically stable along this axis.Moreover,the equilibria atthe endpointsofthe z–axis on the sphere atinfinity,which coincide with the origin I0in the localcharts U3and V3,are unstable(see Subsection 4.1.3). Thus system(1)has two infinite heteroclinic orbits as in[14,17],one of them consisting of the origin O(0,0,0), the positive portion of the z–axis and of one equilibrium on the sphere at infinity(the endpoint of the positive z–axis);the other one consists of the origin,the negative partof the z–axis and of the endpointof the negative z–axis. Particularly,they are shown in Fig.1 and Fig.2.
These discussions finish the proof of Theorem 2.
5 Conclusion
In this paper,after the local stability of equilibrium point E1of a stage-structured predator–prey model is formulated in the critical case a=b+ce,a global analysis at infinity of this model is mathematically presented, including a complete description of the phase portraiton the Poincar′e sphere atinfinity.This mathematicalanalysis leads to two new discoveries:
(1)The parameter d in this model having no effect on finite dynamicalbehaviors of this system bears on the dynamicalbehaviors atinfinity ofthis system;
(2)There existtwo infinite heteroclinic orbits in this model.
Itis hoped thatthe investigationsofthis paperwillbe beneficialforfurtherstudies forsimilarstage-structured predator–prey models,especially with biologicalsignificance.
[1]Chen L,Chen J.Nonlinear BiologicalDynamic Systems[M].Beijing:Science Press,1993.
[2]Chen L.Mathematical Models and Methods in Ecology[M].Beijing:Science Press,1988.
[3]Hofbauer J,Sigmund K.Evolutionary Games and Population Dynamics[M].Cambridge:Cambridge University,1998.
[4]Freedman H I.Deterministic Mathematical Models in Population Ecology[M].New York:Marcel Dekker,1980.
[5]Murray JD.Mathematical Biology[M].2nd corrected Ed.Heidelberg:Springer Press,1993.
[6]Takeuchi Y.GlobalDynamicalProperties of Lotka–Volterra Systems[M].Singapore:World Scientific,1996.
[7]May R M.Stability and Complexity in Model Ecosystems[M].Princeton:Princeton University,1975.
[8]May R M.Theoretical Ecology,Principles and Applications[M].Oxford:Blackwell,1981.
[9]Takeuchi Y,Oshime Y,Matsuda H.Persistence and periodic orbits of a three-competitor model with refuges[J].Math Biosci,1992,108(1):105-125.
[10]Matsuda H,Namba T.Toshiyukico–evolutionarily stable community structure in a patchy environment[J].JTheoret Biol, 1989,136(2):229-243.
[11]Aiello W G,Freedman H I.A time delay model of single–species growth with stage structure[J].Math Biosci,1990, 101:139-153.
[12]Aiello W G,Freedman H I.Analysis of a model representing stage-structured population growth with stage-dependent time delay[J].Siam ApplMath,1992,52:855-869.
[13]Wang W,Chen L.A predator–prey system with stage structure forpredator[J].ComputMath Appl,1997,33(8):83-91.
[14]Messias M.Dynamics atinfinity and the existence of singularly degenerate heteroclinic cycles in the Lorenz system[J].J Phys A:Math Theor,2009,42(11):115101.
[15]Messias M.Dynamics atinfinity ofa cubic Chua′s system[J].InternatJBifur Chaos,2011,21(01):333-340.
[16]Llibre J,Messias M.Globaldynamics ofthe Rikitake system[J].Physica D NonlinearPheonomena,2009,238(3):241-252.
[17]Liu Y.Dynamics at infinity and the existence of singularly degenerate heteroclinic cycles in the conjugate Lorenz–type system[J].Nonlinear Analysis Real World Applications,2012,13(6):2466-2475.
[18]Geng F,Li X.Singular orbits and dynamics atinfinity of a conjugate Lorenz-like system[J].Math Modelling and Anal, 2015,20(2):148-167.
[19]Wang H J,Li X Y.More dynamical properties revealed from a 3D Lorenz-like system[J].Int J Bifur Chaos, 2014,24(10):1450133.
[20]Cima A,Llibre J.Bounded polynomialvector fields[J].Trans Amer Math Soc,1990,318(2):557-579.
[21]Zhang X,Chen L,Neumann A U.The stage–structured predator–prey model and optimal harvesting policy[J].Math Biosci,2000,168(2):201-210.
[22]Zhang Z,Ding T,Huang W,etal.Qualitative Theory of Ordinary DifferentialEquations[M].Beijing:Science Press,1985.

O 175.13 Document code:A Article ID:1000-5137(2017)03-0422-10
10.3969/J.ISSN.100-5137.2017.03.011
date:2017-03-21
This research was supported by the Natural Science Foundation(NSF)of Zhejiang Province (No.LQ13A01 0019);NSF of China(No.61473340);NSF of Zhejiang University of Science and Technology(No.F701108G14).
?Corresponding author:Li Xianyi,professor,reseach area:ordinary differentialequation and dynamicalsystem,E-mail: mathxyli@zust.edu.cn
- 上海師范大學學報·自然科學版的其它文章
- Periodic solutions ofa neutralimpulsive differential equation
- On algebraic convergence of non-elementary discrete subgroups of SL(2,Qp)
- Approximate controllability of semilinear fractional evolution equations of order α (1, 2] with finite delay
- The existence of n-order algebraic curve solutions ofplanar quadratic polynomialsystems
- Comments on new iterative methods for solving linear systems
- Analysis ofa stage-structured mosquito population model

