Theoretical study of spin-forbidden cooling transitions of indium hydride using ab initio methods?
Yun-Guang Zhang(張云光),Hua Zhang(張華),and Ge Dou(竇戈)
School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China
Theoretical study of spin-forbidden cooling transitions of indium hydride using ab initio methods?
Yun-Guang Zhang(張云光)?,Hua Zhang(張華),and Ge Dou(竇戈)
School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China
The feasibility of spin-forbidden cooling of the InH molecule is investigated based on ab initio quantum chemistry calculations.The potential energy curves for thestates of InH are obtained based on multi-reference configuration interaction plus the Davidson corrections method.The calculated spectroscopic constants are in good agreement with the available experimental data.In addition,the influences of the active space and spin–orbit coupling effects on the potential energy curves and spectroscopic constants are also studied.For Reof a3Π0?,a3Π0+,a3Π1,and a3Π2states,the error from large active space is small.The potential energy curve of the A1Π1state is not smooth for small active space.The spin–orbit coupling effects have great influences on the potential well depth and equilibrium internuclear distance of the A1Π state.The Franck–Condon factors and radiative lifetimes are obtained on the basis of the transition dipole moments of thetransitions.Our calculation indicates that thetransition provides a highly diagonally distributed Franck– Condon factor and a short radiative lifetime for the a3Π1state,which can ensure rapid and efficient laser cooling of InH. The proposed laser drivestransitions by using three wavelengths.
spectroscopic constants,Franck–Condon factors,transition dipole moments,spin-forbidden cooling transition
1.Introduction
Laser cooling to create unique ultracold molecules has aroused considerable interest[1–4]because of their promising applications,for example,new platforms for quantum computing,[5]quantum controlled chemistry,[6,7]precision measurement,[8–10]and quantum simulation.[11,12]Naturally the search for potential laser cooling candidates is attracting more and more interest.The direct cooling of a diatomic molecule to the order of microkelvin was firstly achieved in SrF using only three laser beams in 2010,[1]which has initiated a search for more molecules that may be controlled in a similar way.Later,successful laser cooling experiments have been performed for YO,[13]CaF,[14]BH,[15]and BaH.[16]Besides the experimental studies on laser cooling candidates,theoretical optical schemes have been suggested for MgCl,[17]MgBr,[17]BeI,[18]MgI,[18]BeCl,[19]BeBr,[19]BeF,[20]MgF,[21]LiBe,[22]as well as for M H(M=Be,Mg, Ca,Sr,and Ba).[23]According to the previous investigations, the Doppler laser-cooling process must meet these significant criteria:highly diagonal Franck–Condon factors(FCFs),limiting number of lasers required to keep the molecule in a closed-loop cooling cycle,and short radiative lifetime τ describing rapid laser cooling.In theory,most of the studies have focused on spin-allowed transitions(A2Π?X2Σ+or A1Π? X1Σ+).While Kobayashi et al.experimentally confirmed that the spin-forbidden transition B3Π→X1Σ+is well suited for laser cooling of the KRb[3]molecule in 2014.In addition,the laser cooling scheme using the spin-forbidden transition has also been theoretically studied on AlF,[24]BBr,[25]BCl,[25]and LiRb.[26]These results open the door to all-optical production of polar molecules at sub-microkelvin temperatures and highlight the possibility of finding similar molecules that can be laser cooled.
Indium monohalides have been attracting interest for a long time because of their applications in the etching process of semiconductor devices.Experimental studies and theoretical calculations have been performed for InH over the past several decades.In 1939,the electronic spectrum of InH was reported,and bands of two transitions(i.e.,Σ–Σ and Π–Σ) were rotationally analyzed by Grundstr?m.[27,28]Garton[29]presented a band system in the wavelength region of 233–250 nm in 1951,but the system was not assigned.Subsequently,Neuhaus et al.[30,31]measured the A1Π–X1Σ+and a3Π–X1Σ+absorption spectra of InH and obtained the spectroscopic constants.Ginter[32–34]fitted the Rydberg–Klein– Rees curves of,and a3Π1states,and foundandtransitions.Ogilvie[35]later determined the potential energy and coefficients of radialfunc-tions of InH in the ground state X1Σ+from the rovibrational spectrum.In 1993,Rajamanickam et al.[36]refitted the Rydberg–Klein–Rees curves of theand a3Π1states, and obtained the FCFs of thesystem.In 2003, Zou et al.[37]investigated the potential energy curves(PECs) and the spectroscopic constants of the,a3Π0?,a3Π0+, a3Π1,a3Π2,and A1Π1states using the second order CI and relativistic CI methods,and predicted the transition properties of the excited states.Most recently,analytic potential energy functions were computed for theand a3Π0+states of InH using a dict-potenial-fit analysis by Alireza Shayesteh et al.[38]However,a systematic study of laser cooling of InH is, to the best of our knowledge,is so far unavailable.We focus in the present work on the theoretical study of the laser cooling of InH molecule employing different active spaces.The electronic structures and transition properties associated with the laser cooling of InH are calculated,including FCFs,transition dipole moments(TDMs),and radiative lifetimes of thetransitions of the InH molecule.A scheme for a feasible laser cooling cycle of InH is designed briefly.
Section 2 describes the ab initio methods and basis sets used in the calculations of the electronic states of InH.Section 3 presents the results and discussion of the data,outlining laser cooling schemes for InH.We draw a conclusion for this work in Section 4.
2.Computational details
All the ab initio calculations are performed using the MOLPRO package.[39]The electronic states X1Σ+,a3Π,A1Π, and 13Σ+of InH molecule have been calculated with multi-reference configuration interaction(MRCI)plus Davidson corrections(MRCI+Q)method,[40–42]which is based on the complete active space self-consistent-field(CASSCF)[43,44]wave functions.Scalar relativistic effects are included throughout the Douglas–Kroll–Hess[45,46]transformation of the relativistic Hamiltonian.The spin–orbit coupling(SOC) effects are also taken into account following the MRCI+Q calculations for the InH molecule.Due to the limitation of the symmetry of the MOLPRO program package,the computations are performed within the C2νpoint group symmetry, which has four irreducible representations(A1,B1,B2,and A2).In the CASSCF and MRCI+Q calculations,23 or 14 molecular orbitals are chosen as the active space,including eleven or seven a1,five or three b1,five or three b2,and two or one a2symmetry.Fourteen electrons are distributed in(11552) or(7331)active space.The aug-ccpV5Z(AV5Z)basis set is used for the H atom.For the In atom,we take the small-core scalar relativistic effective core potential(ECP)ECP28MDFAV5Z with the corresponding valence basis sets.
The nuclear Schr?dinger equation is solved using the LEVEL 8.2 program[47]to evaluate the spectroscopic constants,including the equilibrium bond length(Re),harmonic and in harmonic vibrational constants(ωeand ωexe),rotational constant(Be),adiabatic relative electronic energy referred to the ground state(Te),and dissociation energy(De)for the ground and the low-lying states of InH.The 13Σ+states are repulsive;therefore,they are not discussed in detail.All PECs are calculated with an interval of 0.05?A over the distance from 1.1?A to 9?A.To obtain accurate results,the interval value is reduced to 0.02?A near the equilibrium bond distance.The permanent dipole moments(PDMs)and TDMs are computed by the MRCI+Q method.The FCFs and radiative lifetimes of the various vibrational levels forandtransitions of InH are also determined from the LEVEL 8.2 program with the PECs and TDMs of different electronic states.
3.Results and discussion
3.1.PECs and spectroscopic constants
In order to understand the possibility of laser-cooling InH molecule,we investigate the X1Σ+,a3Π,A1Π,and 13Σ+states of InH with the lowest dissociation channel In(2P)+ H(2S)at the MRCI+Q level.Because InH is a heavy nuclear molecule,the SOC effects are considered in calculations.The dissociation limit In(2P)+H(2S)splits into two asymptotes, namely,In(2P1/2)+H(2S1/2)and In(2P3/2)+H(2S1/2).These two dissociation limits produce eight ? states.The PECs for theandstates of InH are plotted in Fig.1.The corresponding spectroscopic constants are tabulated in Table 1 along with available experimental data[48]for comparison.
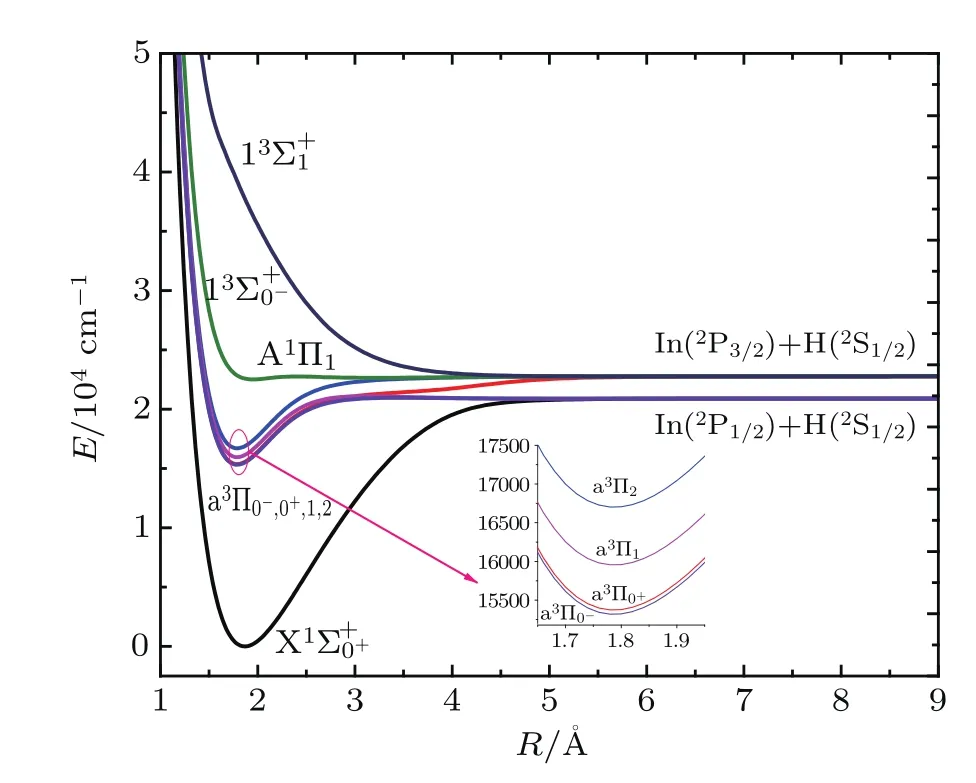
Fig.1.(color online)The PECs including ? splitting of the low-lying electronic states of InH molecule.
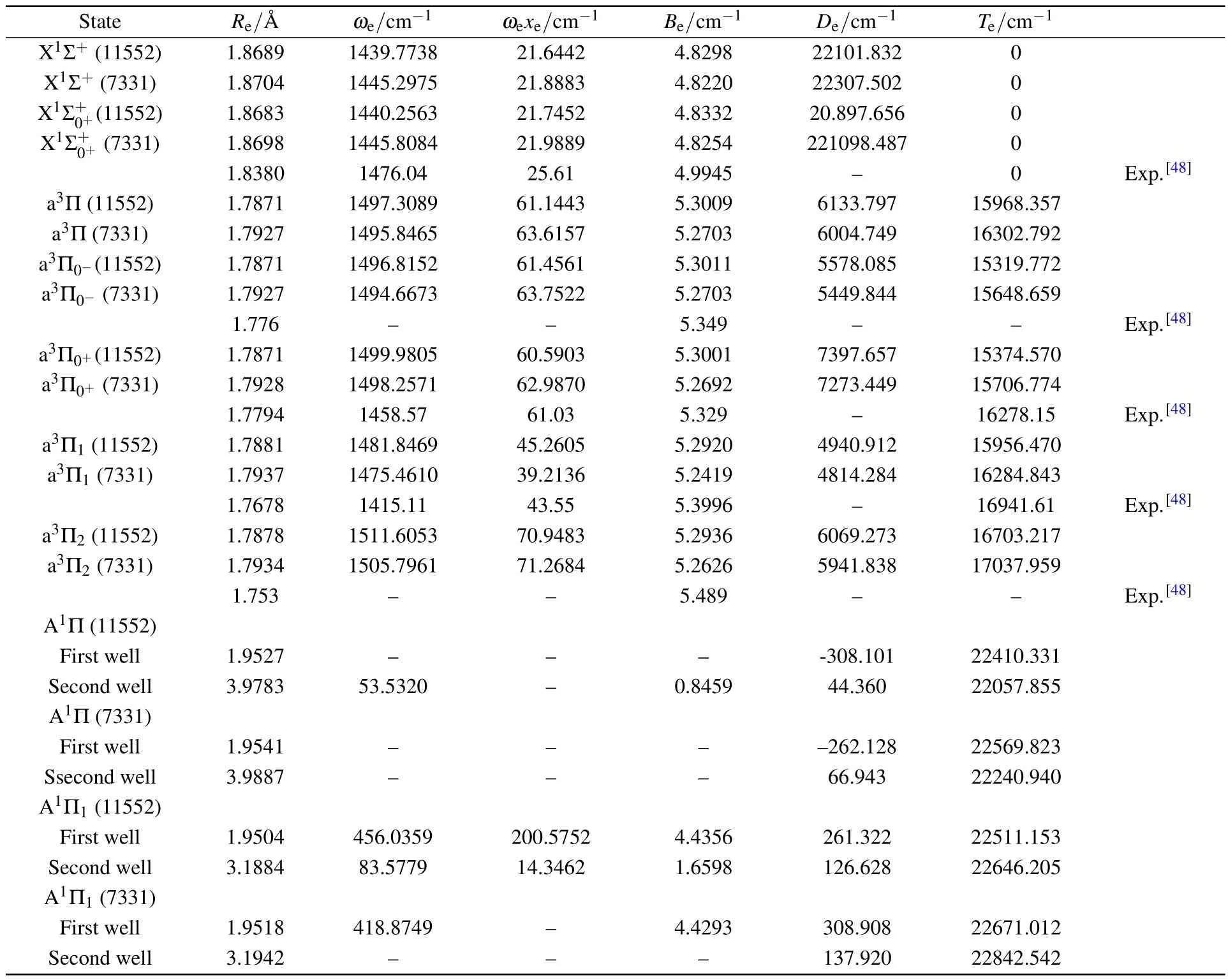
Table 1.Spectroscopic constants for InH molecule at the MRCI+Q level.
As can be seen from Table 1,the influence of the SOC effect on the spectroscopic constants for the ground state seems to be weak.For example,the vibrational frequency ωeand an harmonic vibrational constants ωexeof the X1Σ+state are computed to be 1439.7738 cm?1and 21.6642 cm?1, which differ from the values ofby 0.4825 cm?1and 0.101 cm?1,respectively.The SOC effects are considered in the calculations for the a3Π state,which splits into four ? states(a3Π0?,a3Π0+,a3Π1,and a3Π2).In addition,to obtain accurate results,the effects of the active space are also considered for the InH molecule.The study of spectroscopic constants mainly focuses on two active spaces(11552) and(7331).The active space has a weak influence on the spectroscopic constants of the X1Σ+and a3Π states.For the X1Σ+state,the values of ωeand Befrom active spaces (11552)and(7331)are very close.For the a3Π state,the calculated ωeand Beresults for active space(11552)are only 1.462 cm?1and 0.030 cm?1larger than those for active space(7331).Meanwhile,the effects of the different active spaces(11552)and(7331)on the spectroscopic constants of the ? sub-states,a3Π0?,a3Π0+,a3Π1,and a3Π2are considered.The results indicate that the effects of the active space on the spectroscopic constants of these states are insignificant.The ωevalues of the a3Π0?and a3Π2sub-states for active space(11552)are 1496.8152 cm?1and 1511.6053 cm?1,which are in excellent agreement with the values of 1494.6673 cm?1and 1505.7961 cm?1for active space(7331).Our values of ωexeof the a3Π0?and a3Π2states for active space(11552)are slightly larger than those for active space(7331).Thus the following analyses mainly focus on the results on the basis of active space (11552).For,a3Π0+,and a3Π1states,the equilibrium bond distances Reare calculated to be 1.8683?A,1.7871?A, and 1.7881?A,and the corresponding percentage errors are only 1.65%,0.43%,and 1.15%with respect to the experimental values,respectively;the differences in the rotational constant Befor the three states are 0.1613 cm?1,0.0289 cm?1, 0.1076 cm?1,respectively;and notably,the calculated Tefor the,a3Π0+,and a3Π1states are 0,15374.570 cm?1, and 15956.470 cm?1,which match well with the experimental values of 0,16278.15 cm?1,and 16941.61 cm?1.The spectroscopic constants for the a3Π0?and a3Π2states are also predicted:ωe=1496.8152 cm?1and 1511.6053 cm?1, ωexe=61.4561 cm?1and 70.9483 cm?1.However,the equilibrium distances Reof the,a3Π0?,a3Π0+,a3Π1,and a3Π2states for active space(11552)are respectively 1.8683?A, 1.7871?A,1.7871?A,1.7881?A,and 1.7878?A,which are closer to the experimental data[48]than those for active space(7331). Because the equilibrium separation has an important influence on FCFs,the results from active space(11552)are more suitable to evaluate the effect of laser cooling.
As shown in Fig.2,the influence of the SOC effects and active space on the PECs of the A1Π state is significant.The dissociation limit of the ? state is greater than that of the Λ–S state.The PECs of the active space(11552)are smoother than those of the active space(7331),which implies that active space(11552)is more conducive to research laser cooling.The PECs of the A1Π and A1Π1states have two potential wells.Moreover,the second potential well and the second equilibrium bond length have a distinct change with the SOC effects.It can be seen from Table 1,for the A1Π state,the second well is placed at 22057.855 cm?1above the ground state and the depth is 44.360 cm?1.For the A1Π1state,the second well is placed at 22646.205 cm?1above the ground state, and the depth is 126.628 cm?1.The equilibrium internuclear distances of the second potential well for the A1Π and A1Π1states are 3.9783 cm?1and 3.1884 cm?1,respectively.In addition,the ωe,ωexe,and Beof the first potential well and ωexeof the second potential well cannot be obtained because the A1Π state has two so shallow potential wells that there is only one vibrational level in them.So no experimental data were available for the A1Π and A1Π1states before.
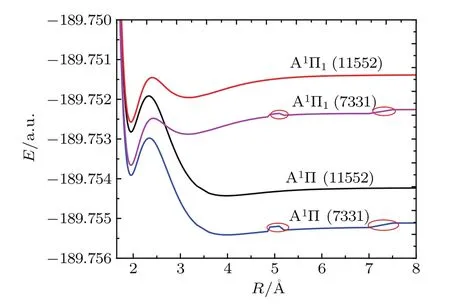
Fig.2.(color online)The PECs for the A1Π and A1Π1 states based on two different active spaces.
3.2.PDMs and TDMs
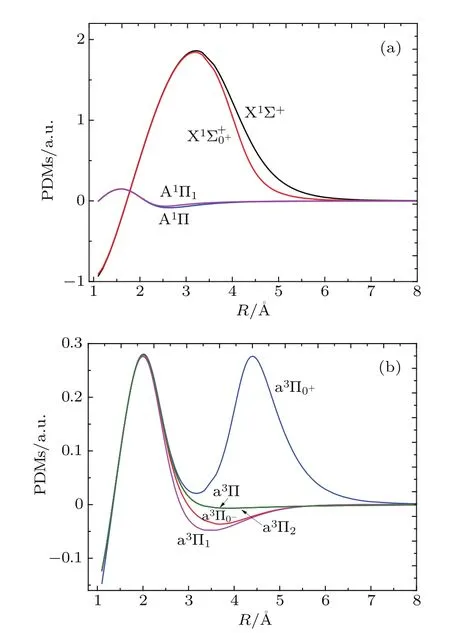
Fig.3.(color online)The PDMs of(a)X1Σ+,,A1Π,A1Π1,and (b)a3Π,a3Π0?,a3Π0+,a3Π1,a3Π2 states of InH molecule.

Fig.4.(color online)The TDMs of the A1Π1→,a3Π0+→,andtransitions of InH molecule.


3.3.FCFs and spontaneous radiative lifetimes
The calculated FCFs can be used to describe the overlap of the vibrational wave functions for the cooling transition. To demonstrate the distributions of FCFs(qν′ν)for the different vibrational states ofandtransitions,we have sketched all possible transitions between 0≤ν≤3 and 0≤ν′≤1 in Table 2 to show the obvious characteristic that the transitions of Δν=ν?ν′=0 have the largest probabilities. Highly diagonal FCFs obey the first criterion to be a potential laser-cooling candidate which could limit the number of lasers required to keep the molecule in a closed-loop cooling cycle. Unfortunately,the FCFs of thetransition are very small.Therefore,it is not possible to cool the InH molecule based on the spin-allowed transition.
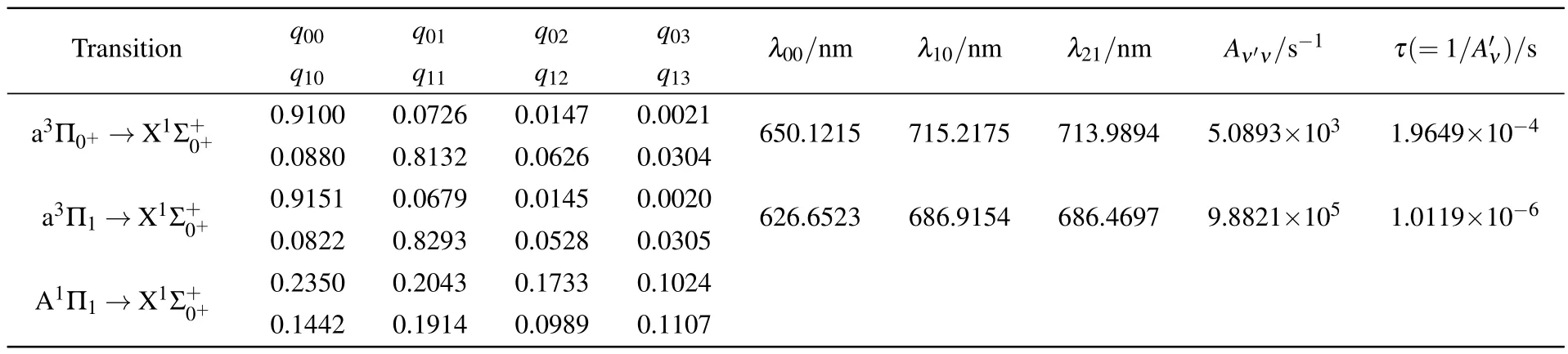
Table 2.The calculated Franck–Condon factors qν′ν,wavelength λνν′,Aν′ν,and estimated spontaneous radiative lifetimes τ.
As listed in Table 2,the present FCFs of the a3Π0+(ν′=andtransitions reach 0.9100 and 0.9151,respectively.The A1Π1state is prohibitive to the cooling cycle because of the small diagonal FCF(q00=0.0235)for thetransition. By comparing with other molecules,our calculated value is slightly larger than that predicted for BeF(q00=0.897),[20]LiRb(q00=0.872),[26]and smaller than that for SrF(q00= 0.98).[1]Therefore,the FCFs of InH are sufficiently large for laser cooling.Aside from the large diagonal FCFs,short spontaneous radiative lifetime τ(10?8–10?5s)[23]is another criterion for the laser cooling of molecules,which can provide a significant rate of rapid cycling.The corresponding computed radiative lifetimes are collected in Table 2.The spontaneous radiative lifetime τ of thetransition is 1.9649×10?4s,which is too long.Yet,the spontaneous radiative lifetime τ of thetransition is 1.0119×10?6s,which is suitable for laser cooling InH molecule.
We also evaluate the branching ratios Rν′ν,which can be expressed asBranching ratios of the diagonal terms R00=0.9357 and R11=0.8403 for thetransition are obtained;and branching ratios of the off-diagonal terms R01=5.78×10?2,R02= 6.37×10?3,R03=1.10×10?4,R10=9.26×10?2,R12= 6.56×10?2,and R13=1.09×10?3are also calculated.Due to the branching to ν≥3 states of InH are expressed as R03+<3×10?5,we propose a cyclic system with three lasers involving ν=0,1,2,3 of thestate and ν′=0,1 of the a3Π1state based on the calculated Rν′ν.The laser driven transitions(solid red)and spontaneous decays(dash line)in the proposed scheme are plotted in Fig 5.The calculated wavelength of the principal laser-driven cycling of thetransition is the main pump in Fig.5,whose wavelength λ00is 626.7 nm.To augment the cooling effect,we add two cycles that the a3Π1(ν′= 0)→(ν=1)transition is the first vibrational pump and the a3Π1(ν′=1)→(ν=2)transition is the second vibrational pump.Therefore,two additional lasers with λ10=686.9154 nm and λ21=686.4697 nm are required.
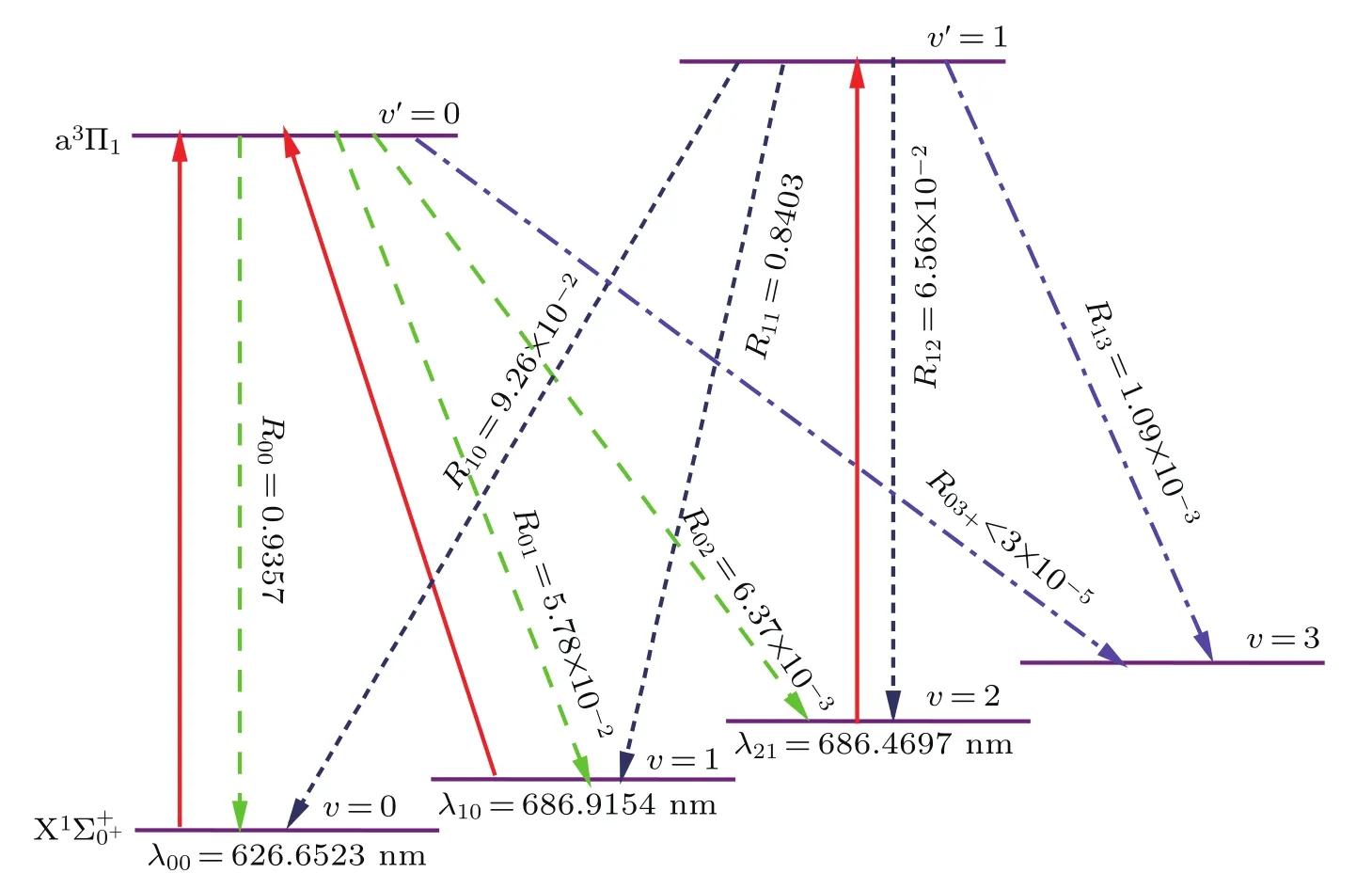
Fig.5.(color online)The proposed laser-driven transition(solid red)and spontaneous decay(dash line)between the a3Π1 and states with calculated Rν′νfor the InH molecule.Here λνν′is the wavelength.
4.Conclusion
[1]Shuman E S,Barry J F and DeMille D 2010 Nature 467 820
[2]Hellwege K H and Hellwege A M 1974 Molecular Constants from Microwave,Molecular Beam,and Electron Spin Resonance Spectroscopy (Berlin:Springer-Verlag)
[3]Kobayashi J,Aikawa K,Oasa K and Inouye S 2014 Phys.Rev.A 89 021401
[4]Molony P K,Gregory P D,Ji Z H,Lu B,Koppinger M P,Le Sueur C R,Blackley C L,Hutson J M and Cornish S L 2014 Phys.Rev.Lett. 113 255301
[5]DeMille D 2002 Phys.Rev.Lett.88 067901
[6]Ospelkaus S,Ni K K,Wang D,Miranda M H G de,Neyenhuis B, Quemener G,Julienne P S,Bohn J L,Jin D S and Ye J 2010 Science 327 853
[7]Krems R V 2008 Phys.Chem.Chem.Phys.10 4079
[8]Flambaum V V and Kozlov M G 2007 Phys.Rev.Lett.99 150801
[9]Hudson J J,Kara D M,Smallman I J,Sauer B E,Tarbutt M R and Hinds E A 2011 Nature 473 493
[10]Isaev T A,Hoekstra S and Berger R 2010 Phys.Rev.A 82 052521
[11]Santos L,Shlyapnikov G V,Zoller P and Lewenstein M 2000 Phys. Rev.Lett.85 1791
[12]Baranov M A,Dalmonte M,Pupillo G and Zoller P 2012 Chem.Rev. 112 5012
[13]Hummon M T,Yeo M,Stuhl B K,Collopy A L,Xia Y and Ye J 2013 Phys.Rev.Lett.110 143001
[14]Zhelyazkova V,Cournol A,Wall TE,Matsushima A,Hudson JJ,Hinds E A,Tarbutt M R and Sauer B E 2014 Phys.Rev.A 89 053416
[15]Hendricks R J,Holland D A,Truppe S,Sauer B E and Tarbutt M R 2014 Frontiers in Physics 2 51
[16]Tarallo M G,Iwata G Z and Zelevinsky T 2016 Phys.Rev.A 93 032509
[17]Wan M J,Shao J X,Gao Y F,Huang D H,Yang J S,Cao Q L,Jin C G and Wang F H 2015 J.Chem.Phys.143 024302
[18]Wan M J,Huang D H,Shao J X,Yu Y,Li S and Li Y Y 2015 J.Chem. Phys.143 164312
[19]Wan M J,Shao J X,Huang D H,Jin C G,Yu Y and Wang F H 2015 Phys.Chem.Chem.Phys.17 26731
[20]Lane I C 2012 Phys.Chem.Chem.Phys.14 15078
[21]Kang S Y,Gao Y F,Kuang F G,Gao T,Du J G and Jiang G 2015 Phys. Rev.A 91 042511
[22]You Y,Yang C L,Wang M S,Ma X G and Liu W W 2015 Phys.Rev. A 92 032502
[23]Gao Y F and Gao T 2014 Phys.Rev.A 90 052506
[24]Wells N and Lane I C 2011 Phys.Chem.Chem.Phys.13 19018
[25]Yang R,Gao Y F,Tang B and Gao T 2015 Phys.Chem.Chem.Phys. 17 1900
[26]You Y,Yang C L,Zhang Q Q,Wang M S,Ma X G and Liu W W 2016 Phys.Chem.Chem.Phys.18 19838
[27]Grundstrom B 1938 Nature 141 555
[28]Grundstrom B 1939 Z.Phys.113 721
[29]Garton W R S 1951 Proc.Phys.Soc.,London,Sect.A 64 509
[30]Neuhaus H 1958 Z.Phys.150 4
[31]Neuhaus H 1958 Z.Phys.152 402
[32]Ginter M L 1963 J.Mol.Spectrosc.11 301
[33]Ginter M L 1966 J.Mol.Spectrosc.20 240
[34]Ginter M L 1965 J.Chem.Phys.42 3222
[35]Ogilvie J F 1992 Chem.Phys.Lett.191 592
[36]Rajamanickam N,Murali T,Sakthivel T,Gomez M F and Gonzalez J J L 1993 Collect.Czech.Chem.Commun.58 1491
[37]Zou W l,Lin M R,Yang X Z and Zhang B Z 2003 Phys.Chem.Chem. Phys.5 1106
[38]Shayesteh A and Ghazizadeh E 2016 J.Mole.Spec.330 72
[39]Werner H J,Knowles P J,Lindh R,Knizia G,Manby F R and Schütz M 2010 MOLPRO,version 2010.1,a package of ab initio programs, see http://www.molpro.net
[40]Laughoff S R and Davidson E R 1974 Int.J.Quantum Chem.8 61
[41]Knowles P J and Werner H J 1988 Chem.Phys.Lett.145 514
[42]Werner H J and Knowles P J 1988 J.Chem.Phys.89 5803
[43]Werner H J and Knowles P J 1985 J.Chem.Phys.82 5053
[44]Knowles P J and Werner H J 1985 Chem.Phys.Lett.115 259
[45]Douglas N and Kroll N M 1974 Ann.Phys.82 89
[46]Hess B A 1986 Phys.Rev.A 33 3742
[47]Le Roy R J 2015“LEVEL 8.2:A computer program for solving the radial Schrodinger equation for bound and quasibound levels,”Chemical Physics Research Report CP-668(University of Waterloo)
[48]Huber K P and Herzberg G 1979 Molecular Spectra and Molecular Structure IV.Constants of Diatomic Molecules(New York:Van Nostrand Reinhold Company Inc.)
7 May 2017;revised manuscript
5 June 2017;published online 18 July 2017)
10.1088/1674-1056/26/9/093101
?Project supported by the National Natural Science Foundation of China(Grant Nos.11104217 and 11402199)and the Program for New Scientific and Technological Star of Shaanxi Province,China(Grant No.2012KJXX-39).
?Corresponding author.E-mail:zygsr2010@163.com
?2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
- Chinese Physics B的其它文章
- Relationship measurement between ac-Stark shift of 40Ca+clock transition and laser polarization direction?
- Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components?
- Collective motion of active particles in environmental noise?
- Temperature dependence of heat conduction coefficient in nanotube/nanowire networks?
- Analysis of dynamic features in intersecting pedestrian flows?
- Heat transfer enhancement in MOSFET mounted on different FR4 substrates by thermal transient measurement?

